傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計技術(shù)研究

喻國瑞，賈良現(xiàn)，黃 珺

(中國直升機設(shè)計研究所，江西 景德鎮(zhèn) 333001)

傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計技術(shù)研究

喻國瑞，賈良現(xiàn)，黃 珺

(中國直升機設(shè)計研究所，江西 景德鎮(zhèn) 333001)

通過先進氣動外形縮比傾轉(zhuǎn)旋翼的動力學(xué)設(shè)計，對傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計中的特殊問題和重點問題形成了系統(tǒng)的研究，并提出了傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)的工程設(shè)計準(zhǔn)則和設(shè)計方法；基于該準(zhǔn)則和方法設(shè)計的縮比傾轉(zhuǎn)旋翼已用于風(fēng)洞試驗。

傾轉(zhuǎn)旋翼；旋翼動力學(xué)；設(shè)計技術(shù)

0 引言

傾轉(zhuǎn)旋翼機是一種同時具備直升機、固定翼飛機特點的新型飛行器。當(dāng)其旋翼處于垂直位置時，傾轉(zhuǎn)旋翼機類似于雙旋翼橫列式直升機，可懸停、側(cè)飛、后飛、垂直起降，此時它的單位功率起降重量接近典型直升機；當(dāng)旋翼處于水平位置時，傾轉(zhuǎn)旋翼機就相當(dāng)于固定翼飛機，能作高速遠(yuǎn)程飛行。因此，傾轉(zhuǎn)旋翼已成為未來最具發(fā)展前景的飛行器之一[1]。

旋翼是傾轉(zhuǎn)旋翼機的主要升力系統(tǒng)(直升機模式)、推進系統(tǒng)(飛機模式)和重要飛行控制執(zhí)行系統(tǒng)，在工程設(shè)計中占有重要地位。在傾轉(zhuǎn)旋翼設(shè)計的第一階段，須非常謹(jǐn)慎地對旋翼動力學(xué)部件進行結(jié)構(gòu)動力學(xué)特性設(shè)計，這項工作與槳葉對于周期諧波載荷的動力學(xué)響應(yīng)密切相關(guān)[2]，設(shè)計的好壞直接關(guān)系到結(jié)構(gòu)的振動和壽命。

傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計技術(shù)是指運用現(xiàn)代設(shè)計理論，結(jié)合經(jīng)驗，經(jīng)過創(chuàng)造性的思維、規(guī)劃及合理的設(shè)計計算，使旋翼結(jié)構(gòu)動力學(xué)設(shè)計滿足傾轉(zhuǎn)旋翼功能和性能要求的技術(shù)。本文基于先進氣動外形傾轉(zhuǎn)旋翼的設(shè)計，研究總結(jié)了傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計的重要內(nèi)容和方法，完成的先進氣動外形縮比傾轉(zhuǎn)旋翼已成功用于風(fēng)洞試驗。

1 設(shè)計技術(shù)研究

本文首先研究總結(jié)了影響傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計的特殊因素和旋翼的構(gòu)型選擇問題，之后研究了槳葉等效邊界條件和動力學(xué)建模方法，并基于該方法研究了旋翼槳葉的耦合模態(tài)，最后總結(jié)研究了調(diào)頻設(shè)計準(zhǔn)則(圖1)。

1.1 影響結(jié)構(gòu)動力學(xué)設(shè)計的特殊因素

傾轉(zhuǎn)旋翼機特殊的工況及氣動外形是造成其結(jié)構(gòu)動力學(xué)設(shè)計特殊性的來源，貫穿整個旋翼結(jié)構(gòu)動力學(xué)設(shè)計。

1.1.1 特殊工況

傾轉(zhuǎn)旋翼機具有飛機和直升機兩種飛行模式，因此其旋翼具備了多種特殊工況，經(jīng)過設(shè)計梳理，兩種模式下對旋翼結(jié)構(gòu)動力學(xué)設(shè)計有重要影響的工況為：

1) 具有2個工作轉(zhuǎn)速。傾轉(zhuǎn)旋翼機為實現(xiàn)較高前飛推進效率，在飛機模式下旋翼轉(zhuǎn)速會較直升機模式時低。通常，飛機模式旋翼轉(zhuǎn)速比直升機模式降低約25%～40%[3]。

2) 旋翼工作總距范圍大。在直升機模式時，一般使用總距不會超過15°，而在飛機模式時，總距能達(dá)到35°～ 60°[4]。

3) 氣動環(huán)境差異性大。在直升機模式時，旋翼的入流不垂直于槳盤平面，存在明顯的周期氣動激勵，旋翼具有周期變距功能，在無窮遠(yuǎn)處垂直于槳盤的氣流速度為0；而對于飛機模式，旋翼入流則垂直于槳盤平面，旋翼無需周期變距，無窮遠(yuǎn)處垂直于槳盤的氣流速度為前飛速度。

1.1.2 特殊氣動外形

旋翼氣動性能主要取決于旋翼槳葉的氣動外形，而傾轉(zhuǎn)旋翼的特殊氣動外形對旋翼結(jié)構(gòu)動力學(xué)設(shè)計有著重要影響。旋翼槳葉氣動外形的特殊性如下：

1) 為兼顧懸停和前飛時的旋翼性能，其槳葉結(jié)構(gòu)扭角可達(dá)40deg甚至更大；

2) 旋翼實度大于常規(guī)直升機，達(dá)到0.14甚至更高，這就使得相同旋翼半徑下，槳葉的結(jié)構(gòu)絕對厚度更大。

這樣的槳葉外形結(jié)合特殊的旋翼轉(zhuǎn)速設(shè)計能夠優(yōu)化來流攻角，保證直升機模式與飛機模式均具有合理的升力(拉力)、阻力特性，但這正是傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計特殊性的重要來源(圖2)。

1.2 旋翼構(gòu)型選擇

旋翼構(gòu)型選擇則決定了動力學(xué)設(shè)計技術(shù)研究的方向，是后續(xù)研究的基礎(chǔ)。不同旋翼構(gòu)型具有不同的旋翼動力學(xué)特性，其設(shè)計分析方法也隨之不同。傾轉(zhuǎn)旋翼機存在直升機模式、飛機模式以及兩種模式切換的過渡飛行狀態(tài)；在飛機模式下旋翼轉(zhuǎn)速降低25%～40%，旋翼離心力作用明顯降低，采用傳統(tǒng)鉸接式旋翼會形成一個較大的穩(wěn)態(tài)錐度角，降低飛機模式下旋翼的推進效率。此外，傾轉(zhuǎn)旋翼安裝在機翼端部，從安全性考慮，須保證在過渡狀態(tài)和飛機模式下，旋翼受到擾動后槳葉不產(chǎn)生過大揮舞。因此，傾轉(zhuǎn)旋翼須使用一種揮舞較為剛硬的旋翼。另一方面，機翼是典型的柔性支持系統(tǒng)，因此傾轉(zhuǎn)旋翼的構(gòu)型選擇應(yīng)考慮盡可能降低柔性支持系統(tǒng)帶來的耦合影響，如：地面共振、回轉(zhuǎn)顫振等問題。

經(jīng)過設(shè)計梳理，傾轉(zhuǎn)旋翼機旋翼構(gòu)型選擇應(yīng)主要考慮四個方面：

1) 盡量避免各種飛行姿態(tài)下槳葉出現(xiàn)過大揮舞；

2) 盡量提高飛機模式下旋翼的推進效率(此時旋翼作為推進系統(tǒng))；

3) 從構(gòu)型上盡可能多地消除不穩(wěn)定可能性，降低設(shè)計復(fù)雜度和風(fēng)險；

4) 盡量降低槳葉根部結(jié)構(gòu)載荷以提高結(jié)構(gòu)壽命。

當(dāng)前我國的傾轉(zhuǎn)旋翼在構(gòu)型上宜采用萬向鉸式旋翼。從結(jié)構(gòu)設(shè)計、新材料、主動控制技術(shù)的發(fā)展來看，若未來能在技術(shù)上解決上述需求，則旋翼構(gòu)型選擇將更加靈活。本文中的傾轉(zhuǎn)旋翼設(shè)計就使用了三片槳葉萬向鉸旋翼(圖3)。

萬向鉸構(gòu)型的旋翼沒有獨立的水平鉸，無擺振鉸，容易設(shè)計成擺振剛硬旋翼，避免了傾轉(zhuǎn)旋翼復(fù)雜的地面共振問題，弱化了旋翼旋轉(zhuǎn)面內(nèi)模態(tài)與支持系統(tǒng)的耦合；另一方面，萬向鉸旋翼能保證飛機模式時旋翼具有較小的穩(wěn)態(tài)錐度角。此外，萬向鉸旋翼的動載荷相對無鉸旋翼更小，對槳葉根部的受載有利；其槳盤傾斜直接由旋轉(zhuǎn)平面傾斜完成，不會造成擺振面內(nèi)的科氏力，這對于前飛狀態(tài)非常有利[5]。

1.3 動力學(xué)建模

為計算分析旋翼動力學(xué)特性，需對傾轉(zhuǎn)旋翼進

行動力學(xué)建模。傾轉(zhuǎn)旋翼槳葉通常具有40°以上的結(jié)構(gòu)負(fù)扭轉(zhuǎn)，槳轂還可能有一定的預(yù)錐角，槳葉通常還具有一定的上反角、下反角及比較大的后掠角，槳葉結(jié)構(gòu)復(fù)雜。本文對傾轉(zhuǎn)旋翼動力學(xué)建模如下：

1)將槳葉離散為一系列的具有不同上反下反角及前略后掠角的Eurler-Bernoulli直梁單元，各梁單元的彈性軸為直線，相鄰單元的彈性軸首尾相接。

2)為了方便描述旋轉(zhuǎn)槳葉的空間位置及運動變形，建立一系列的參考坐標(biāo)系，便于使用哈密頓原理導(dǎo)出動力學(xué)方程[6-7]。槳轂坐標(biāo)系以下標(biāo)h標(biāo)識，旋轉(zhuǎn)坐標(biāo)系以下標(biāo)r標(biāo)識，相對槳轂坐標(biāo)系軸旋轉(zhuǎn)ψ方位角。未變形槳葉坐標(biāo)系以下標(biāo)u標(biāo)識，相對旋轉(zhuǎn)坐標(biāo)系Jr軸有βG+βP的仰角，βG為萬向鉸揮舞角,βP為預(yù)錐角。槳葉變距軸線坐標(biāo)系下標(biāo)p，未變形槳葉坐標(biāo)系下標(biāo)c，槳葉單元坐標(biāo)系下標(biāo)k，變形剖面坐標(biāo)系下標(biāo)d。

各坐標(biāo)系間的轉(zhuǎn)換關(guān)系矩陣為：

(1)

(2)

(3)

其中，θcon為控制槳距輸入，Kβ為揮舞變矩調(diào)節(jié)系數(shù)，θs為變矩鉸彈性變形。

(4)

其中，Λ1k是后掠角，Λ2k是上反角，Λ3k是結(jié)構(gòu)扭轉(zhuǎn)角。

其中，θt是結(jié)構(gòu)扭轉(zhuǎn)角，φ是彈性扭轉(zhuǎn)角。

3)由哈密頓原理導(dǎo)出傾轉(zhuǎn)旋翼氣彈動力學(xué)方程：

(6)

其中：

(7)

(8)

(9)

(10)

(11)

mb為槳葉線密度

(12)

(13)

(14)

(15)

(16)

(17)

(18)

{Xkio,Ykio,Zkio}T分別為第i片槳葉的第k個單元彈性軸的首節(jié)點在未變形槳葉坐標(biāo)系內(nèi)的位置坐標(biāo)；s為單元坐標(biāo)系內(nèi)的局部坐標(biāo)；{u,v,w}T為第i片槳葉的第k個單元(s,0,0)處彈性軸的彈性位移；ue為彈性伸長。

4)通過求解該非線性動力學(xué)方程，即可得到傾轉(zhuǎn)旋翼的結(jié)構(gòu)動力學(xué)特性。

1.4 槳葉等效邊界條件

全耦合的3葉萬向鉸旋翼除考慮槳葉自身動力學(xué)問題外，還須考慮槳葉之間的剛?cè)狁詈蟿恿W(xué)問題，使得設(shè)計復(fù)雜化。為簡化模型以適應(yīng)工程設(shè)計，本文將槳葉根部約束邊界條件等效為固支邊界和鉸支邊界來構(gòu)造“周期型”和“集合型”模態(tài)，并得到如下結(jié)論：三葉萬向鉸的揮舞不存在絕對的鉸支邊界條件，但存在弱固支約束邊界，一定程度上可近似看成鉸支邊界；其完全的固支邊界條件是存在的。

在旋轉(zhuǎn)坐標(biāo)系中，設(shè)第m片槳葉根部揮舞力矩按級數(shù)展開為：

(19)

設(shè)每片槳葉處在等同的周期氣動環(huán)境中：

(20)

以其中一片槳葉揮舞為基準(zhǔn)，在槳轂中心處力矩合成即為該片槳葉總的力矩(揮舞、擺振、扭轉(zhuǎn))。

則揮舞力矩為：

即：

(21)

擺振力矩為：

(22)

操縱載荷為：

(23)

當(dāng)系數(shù)為2時為集合型運動：其擺振運動表現(xiàn)為扭振系統(tǒng)整體頻率，其扭轉(zhuǎn)運動表現(xiàn)為總距操縱剛度下的頻率。

當(dāng)系數(shù)為0時擺振表現(xiàn)為完全固支邊界條件下的頻率，擺振運動支持結(jié)構(gòu)不發(fā)生耦合；扭轉(zhuǎn)表現(xiàn)為與橫/縱向周期操縱剛度匹配的頻率。邊界條件系數(shù)表如表1。

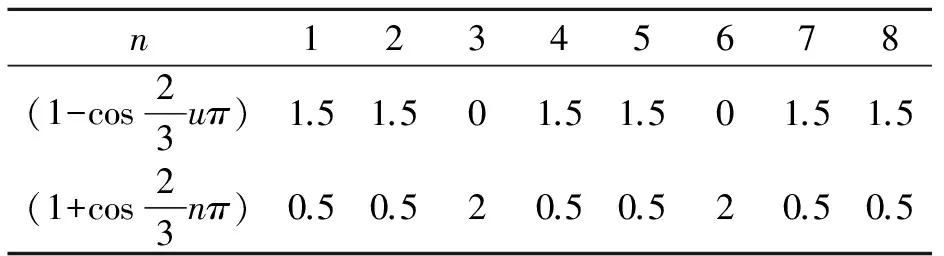
表1 邊界條件系數(shù)表

故當(dāng)n為3的倍數(shù)時，為揮舞為固支邊界條件，當(dāng)n=1、2、4、5、7……時不存在完全鉸接邊界條件，此時系數(shù)為1.5，為近似鉸接的支持條件。因此，三槳葉萬向鉸式傾轉(zhuǎn)旋翼設(shè)計可使用特殊的共振圖(圖4)。

1.5 旋翼槳葉的耦合模態(tài)

槳葉的模態(tài)識別是旋翼結(jié)構(gòu)動力學(xué)分析的重要內(nèi)容，槳葉模態(tài)特性的不同決定了系統(tǒng)的響應(yīng)特性。

研究發(fā)現(xiàn)，傾轉(zhuǎn)旋翼大范圍的總距和轉(zhuǎn)速變化，加之槳葉的大結(jié)構(gòu)扭角造成了揮舞模態(tài)、擺振模態(tài)和扭轉(zhuǎn)模態(tài)之間強烈的耦合，這種耦合還伴隨著總距而變化，使得槳葉模態(tài)呈現(xiàn)出特殊性質(zhì)。

圖5和圖7分別為傾轉(zhuǎn)旋翼周期型和集合型模態(tài)中的模態(tài)振型包絡(luò)線，其中第一個case表示-4°總距，最后一個case為52°總距；圖6和圖8分別對應(yīng)了-4°～52°總距范圍內(nèi)周期型和集合型各階模態(tài)頻率變化。可以得到如下規(guī)律：

1) 頻率8Ω以下的周期型第2階、第3階模態(tài)，集合型第1階、第2階模態(tài)的揮舞和擺振具有強烈的耦合，不能直接判定其為揮舞模態(tài)或擺振模態(tài)，建議稱其耦合模態(tài)。

2) 周期型第2階、第3階模態(tài)均同時表現(xiàn)出揮舞2階和擺振1階模態(tài)的特性。第2階在小總距時以揮舞特性為主，在大總距時以擺振特性為主，第3階在各個總距下?lián)]舞和擺振相當(dāng)。

3) 周期型第2階模態(tài)頻率隨總距升高迅速降低；周期型第3階模態(tài)頻率隨總距升高呈現(xiàn)先迅速提高后迅速降低的規(guī)律；扭轉(zhuǎn)一階頻率在10°以下趨于平穩(wěn)，之后隨總距的升高呈現(xiàn)先降低后增高的規(guī)律。周期型第3階和扭轉(zhuǎn)1階頻率變化的拐點十分接近。

4) 集合型則是第1階、第2階模態(tài)同時表現(xiàn)出揮舞和擺振的耦合特征，不同之處在于集合型第1階表現(xiàn)的是揮舞1階和擺振1階的特性，集合型第2階與周期型第3階類似，表現(xiàn)出揮舞2階與擺振1階模態(tài)的特性。第1階在小總距時以揮舞特性為主，在大總距時以擺振特性為主，第2階在各個總距下?lián)]舞和擺振相當(dāng)。

5) 集合型第1階模態(tài)頻率隨總距升高緩慢降低；集合型第2階模態(tài)頻率隨總距的升高呈現(xiàn)先緩慢降低，在大總距時迅速降低后又升高的趨勢；扭轉(zhuǎn)1階與耦合2階的特性類似，頻率隨總距的升高呈現(xiàn)先緩慢降低，在大總距時迅速降低后又升高的趨勢。

1.6 旋翼頻率設(shè)計準(zhǔn)則

調(diào)頻設(shè)計是旋翼結(jié)構(gòu)動力學(xué)設(shè)計的主要目標(biāo)之一。傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)特性與強結(jié)構(gòu)耦合(槳葉大結(jié)構(gòu)扭角、大變距范圍引起)和大范圍的旋翼轉(zhuǎn)速變化緊密聯(lián)系，這種強烈的耦合使得常規(guī)直升機旋翼的按照揮舞和擺振分開調(diào)頻的辦法不再適用，同時，這使得按照傳統(tǒng)設(shè)計要求的避開nΩ進行調(diào)頻設(shè)計將使得設(shè)計無法開展[8，9]。根據(jù)上述研究，提出了三槳葉萬向鉸旋翼初步設(shè)計時的結(jié)構(gòu)動力學(xué)設(shè)計準(zhǔn)則如下：

1) 根據(jù)槳葉邊界條件將旋翼模態(tài)分為周期型和集合型進行計算。鉸支邊界為周期型模態(tài)，固支邊界為集合型模態(tài)。

2) 在直升機模式額定轉(zhuǎn)速、飛機模式額定轉(zhuǎn)速等工作停留轉(zhuǎn)速下，集合型模態(tài)固有頻率僅須避開1Ω、3Ω、6Ω；周期型模態(tài)除揮舞1階外，其它固有頻率僅須避開1Ω、2Ω、4Ω、5Ω。

3) 當(dāng)某個使用狀態(tài)中周期型1階模態(tài)以擺振特征為主時，模態(tài)頻率須大于1.25Ω。

4) 任何周期型模態(tài)頻率配置距2Ω和4Ω的氣動載荷激勵0.25Ω以上。

5) 任何集合型模態(tài)頻率配置距3Ω和6Ω氣動載荷激勵0.15Ω以上。

6) 對于6/rev及以上的高頻模態(tài)的頻率配置，要求較為放松，初步設(shè)計時不作特殊要求。

7) 在設(shè)計之初必須首先明確直升機模式和飛機模式的旋翼額定轉(zhuǎn)速和其它停留轉(zhuǎn)速；

8) 由于變距對動力學(xué)特性的影響十分突出，故在設(shè)計之初就要明確對應(yīng)轉(zhuǎn)速下需要穩(wěn)定使用的總距邊界。需要注意的是與直升機旋翼設(shè)計不同，保守過大的總距使用范圍是不可取的。

上述第3-6條所確定的設(shè)計邊界是工程設(shè)計初期的重要參考，但隨著設(shè)計工作的詳細(xì)深入，可通過載荷分析等手段逐步放寬要求。

此設(shè)計準(zhǔn)則最大的意義是擴展了傾轉(zhuǎn)旋翼的頻率配置可行區(qū)間，使得對總距十分敏感的傾轉(zhuǎn)旋翼固有頻率的調(diào)頻設(shè)計成為了可能，解決了由于傳統(tǒng)旋翼動力學(xué)設(shè)計準(zhǔn)則導(dǎo)致的使用限制。

2 工程設(shè)計案例

旋翼型式：萬向鉸

槳葉片數(shù)：3

旋翼實度：0.144

槳葉結(jié)構(gòu)扭角：35°(非線性扭轉(zhuǎn))

變距活動范圍：0°～50°

飛機模式：35°～50°

直升機模式：0°～15°

萬向鉸揮舞活動范圍：-10°～ +10°

工況：各個設(shè)計總距下進行風(fēng)洞試驗

使用本文方法，結(jié)構(gòu)動力學(xué)設(shè)計結(jié)果見表2和表3。圖9為該縮比旋翼進行風(fēng)洞測試。

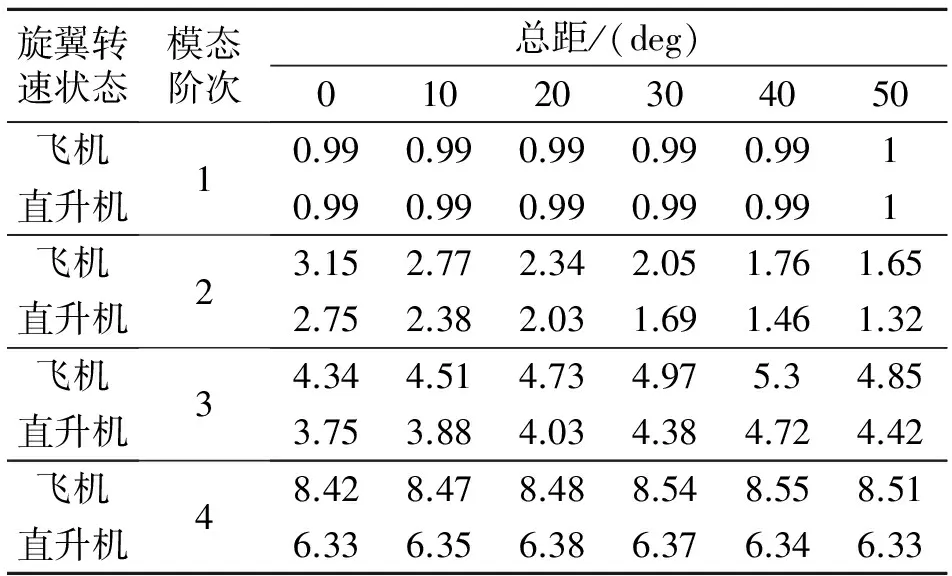
表2 周期型頻率比計算結(jié)果

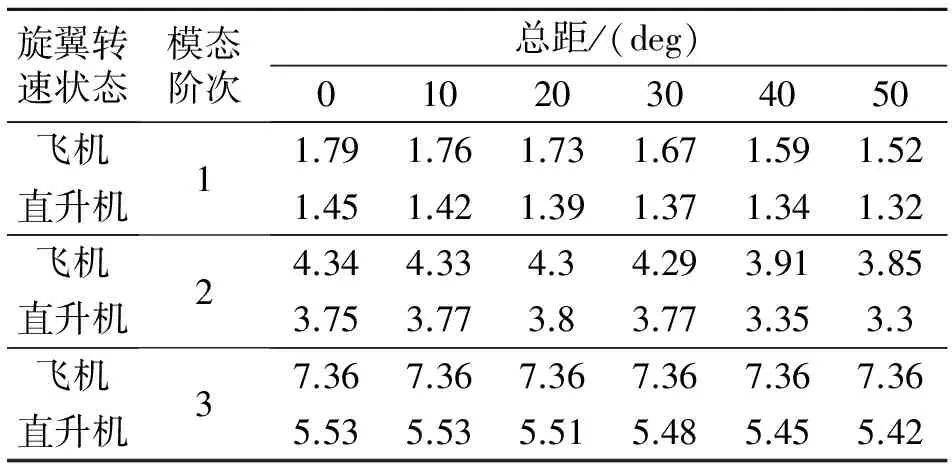
表3 集合型頻率比計算結(jié)果

3 總結(jié)

本文緊密結(jié)合實際工程設(shè)計，研究總結(jié)了傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)設(shè)計中所需考慮的重要問題，建立了傾轉(zhuǎn)旋翼動力學(xué)模型，研究總結(jié)了適用于工程實際的設(shè)計思路和設(shè)計準(zhǔn)則，這些研究揭示了傾轉(zhuǎn)旋翼的結(jié)構(gòu)動力學(xué)特點，涵蓋了傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)工程設(shè)計的重要內(nèi)容和方法，基于此設(shè)計的縮比模型旋翼成功用于風(fēng)洞試驗，有力地支持了本文的研究結(jié)果。得出結(jié)論如下：

1) 本文建立的動力學(xué)模型適用于萬向鉸式傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)計算分析；

2) 本文提出的邊界條件處理方法和模態(tài)特性研究對深入認(rèn)識萬向鉸式傾轉(zhuǎn)旋翼動力學(xué)特性有重要意義；

3) 本文提出的設(shè)計準(zhǔn)則可用于指導(dǎo)三葉萬向鉸式傾轉(zhuǎn)旋翼結(jié)構(gòu)動力學(xué)工程設(shè)計。

[1] 徐 敏. 傾轉(zhuǎn)旋翼機的發(fā)展與關(guān)鍵技術(shù)綜述[J]. 直升機技術(shù), 2003(2):40-44.

[2] 張曉谷. 直升機動力學(xué)設(shè)計[M]. 北京: 航空工業(yè)出版社, 1995: 4-45.

[3] Warwick G. Opposing Tilt [J]. Aviation Week & Space Technology, October 14/21, 2013:1-2.

[4] 王 偉, 段卓毅, 周 林. 傾轉(zhuǎn)旋翼機設(shè)計特點及難點淺析[J]. 航空科學(xué)與技術(shù), 2015(3):1-4.

[5] 張呈林, 張曉谷, 郭士龍, 等. 直升機部件設(shè)計[M]. 南京：南京航空學(xué)院, 2008.

[6] Srinivas V, Chopra I, Nixon W. Aeroelastic Analysis of advanced Geometry Tiltrotor Aircraft [J]. Journal of the American Helicopter Society, 2013,43(3):212-221.

[7] Srinivas V, Chopra I. Formulation of a Comprehensive Aeroelastic Analysis for Tiltrotor Aircraft [R]. AIAA-96-1546-CP.

[8] Popelka D A, Agnihotri A. Bell Helicopter Textron Inc. Prediction and Alleviation of V-22 Rotor Dynamic Loads [C]. American Helicopter Society, November 1989:55-79.

[9] Agnihotri A, Schuessler W, Marr R. V-22 Aerodynamic Loads Analysis and Dvelopment of Loads Alleviation Flight control System [C]. American Helicopter Society 4lth Annual Forum, Boston, Massachusetts, May 1989:32-53.

Research and Development of Tilt-rotor Structure Dynamic Design

YU Guorui, JIA Liangxian, HUANG Jun

(China Helicopter Research and Development Institute, Jingdezhen 333001, China)

Important and special structure dynamic problem had systemic researched in a project which used 3 advanced geometry blades on a scaled tilt-rotor design. The design criteria of tilt-rotor structure dynamic had been presented. The scale rotor which followed the criteria had work in wind tunnel test.

tilt-rotor； rotor dynamic；design.

2016-11-10

863計劃“先進直升機技術(shù)”(2012AA112201)。

喻國瑞(1989-)，男，貴州貴陽人，本科，助理工程師，研究方向為旋翼系統(tǒng)動力學(xué)設(shè)計、復(fù)合材料旋翼槳葉結(jié)構(gòu)設(shè)計。

1673-1220(2017)01-001-07

V224；V214

A