多介質流體力學計算的譜體積方法＊

劉 娜，陳藝冰

（1.北京應用物理與計算數學研究所，北京100088；2.中國工程物理研究院高性能數值模擬軟件中心，北京100088；3.北京應用物理與計算數學研究所計算物理實驗室，北京100088）

多介質流體力學計算的譜體積方法＊

劉 娜1，2，3，陳藝冰1，3

（1.北京應用物理與計算數學研究所，北京100088；2.中國工程物理研究院高性能數值模擬軟件中心，北京100088；3.北京應用物理與計算數學研究所計算物理實驗室，北京100088）

針對高維及多物理耦合計算耗費大等困難，設計適合多介質流動模擬的模板緊致、易于并行、高階精度、計算耗費小的譜體積方法。該方法是求解雙曲型守恒率譜體積方法的直接推廣，針對多介質流動物質界面捕捉的困難，利用擬守恒格式的思想避免物質界面處的非物理振蕩。數值模擬結果表明，本方法具有高階精度、高分辨率，且節約計算量，并且可以有效避免物質界面處非物理振蕩。

流體力學；譜體積方法；高精度；剛性氣體；多介質；模板緊致

多介質流體力學的模型可以用擴展歐拉方程組描述。早期，使用守恒格式直接求解，但在接觸間斷（物質界面）附近，會產生非物理的壓力和速度振蕩。隨后，很多學者對此進行分析，并提出各種補救措施［1－2］，其中R.Abgrall等提出的擬守恒型格式，由于其簡單、健壯得到了廣泛應用。此后，K.M.Shyue［3－4］、Y.B.Chen等［5］進一步發展了這個方法。這些工作通常采用MUSCL限制器，精度不超過二階。

當前，實際工程問題中對精細化設計提出越來越高的要求，不少更高階（高于2階）精度的格式被應用于求解多介質問題。其中，E.Johnsen等［6］將WENO格式推廣于求解擴展歐拉方程組，取得成功。他的算法極大提高了對物質界面的分辨率，但WENO格式進行重構時，需要利用目標單元及其周圍單元的信息，隨著格式階數的增大，需要不斷擴展模板，在高維情形復雜度將急劇增加。J.Zhu等［7］采用DG格式來求解這個問題。與WENO相比，DG格式僅采用局部模板即可獲得高精度。實際上，DG格式是近年來廣受關注的高精度緊致格式的典型代表之一。除了DG方法之外，譜體積（SV）格式［8－9］也是一類成功的高精度緊致格式。它是譜方法和有限體積方法的結合體，其主要思想是根據細分的控制體的單元均值，重構出譜體積元中的近似解。本質上，DG方法和SV方法都是采用目標單元內部信息來獲得網格單元內解的逼近，因此模板都較為緊致，且在并行計算時不需要通信周圍單元的信息，是一種高并行度的格式。與DG方法相比，SV方法的一個優點在于節省了表面積分和體積分的計算，并且根據Z.J.Wang［8］的分析，SV方法對CFL數的限制也更低。

本文中，針對高維及多物理耦合計算耗費大等困難，設計適合多介質流動模擬的譜體積方法。

1 控制方程

非定常可壓縮流體可以用歐拉方程來描述，以一維為例可以記為：W／t＋F（W）／x＝0，其中W＝（ρ，ρu，ρE）T，F（W）＝（ρu，ρu2＋p，（ρE＋p）u）T。剛性氣體狀態方程為p＝（γ－1）ρe－γp，其中γ為比熱比，p為參考壓力。由于流體流動時狀態量γ隨著流動保持不變，因此滿足［10］：γ／t＋uγ／x＝0。定義質量比分Y＝ρ1／（ρ1＋ρ2），建立γ與Y的關系：則質量比分同樣滿足：

式中：W＝（ρ，ρu，ρE，ρY）T，F（W）＝（ρu，ρu2＋p，（ρE＋p）u，ρuY）T。

2 守恒譜體積方法

直接將譜體積方法推廣應用于多介質Euler方程組（2）。下面給出格式設計的基本框架：將計算區域Ω劃分為N個子區間｛Si＝［xi－1／2，xi＋1／2］Ω，i∈Z｝，每個Si稱為譜體積元，hi＝xi＋1／2－xi－1／2表示其區間長度。假設要設計一個k階精度格式，則將每個譜體積元Si進一步分化成k個控制體，即Ci，j＝（xi，j－1／2，xi，j＋1／2），j＝1，…，k。在每個控制體上定義控制體單元平均值tn）dx，j＝1，…，k。將控制方程（2）在Ci，j上積分，可以得到如下半離散格式：

要完成k階譜體積格式，還需要3個步驟。

步驟1：重構。利用給定的tn時刻的控制體單元平均值進行重構。在每個譜體積單元Si內部，由k個控制體的單元平均值，重構出在譜體積元Si內的一個至多k－1次多項式Wni（x）。這樣得到的重構多項式可能會引起數值振蕩，為了避免高階重構帶來的數值振蕩，對重構多項式利用基于原始變量的修正TVB minmod斜率限制器的思想進行限制。詳細過程可以參見文獻［8］。經過限制，在整個計算區域的重構函數具有如下性質：（1）在譜體積單元內部不需要限制的控制體界面處，重構多項式函數是連續的；（2）在譜體積單元界面處或譜體積單元內部限制器起作用的控制體單元界面處，重構多項式函數是間斷的。

步驟2：計算數值通量。根據重構多項式的性質，在譜體積單元內部狀態連續的控制體單元界面處，直接使用連續的數值通量，而在譜體積單元界面處以及譜體積單元內部經過限制后的控制體單元界面處，由于兩側的狀態值不同，使用間斷數值通量。常用的數值通量計算方法，如Lax－Friedrichs、HLLC、Roe、BGK通量等都可以使用，本文中選擇最簡便的Lax－Friedrichs數值通量。

步驟3：時間方向離散。時間方向可以采用4階Runge－Kutta方法離散。

3 穩定性分析

根據第2節譜體積方法在多介質守恒擴展歐拉方程組上的直接推廣計算多介質問題，會產生物質界面處壓力、速度的非物理振蕩。在第5.2節將顯示一維多介質運動界面問題的計算結果。R.Abgrall等［1－2］指出，這些非物理振蕩是由于對組分方程的守恒離散造成的。下面以Lax－Friedrichs通量為例進行分析，為了簡便起見，時間方向考慮Euler方法離散，則質量、動量、能量方程的離散可以表示為：

若n時刻速度u＝u0和壓力p＝p0為常數，則根據（5）結合（4），可得：，即在n＋1時刻速度可以保持常數：進一步，將狀態方程代入（6），則n＋1時刻滿足

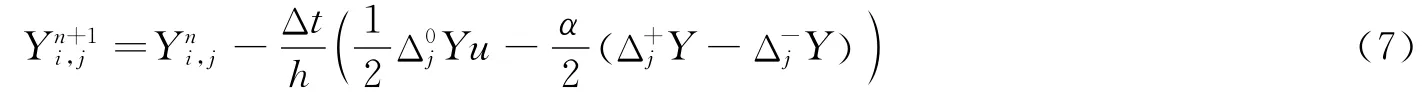
4 擬守恒譜體積方法

根據第3節的穩定性分析，對第2節中的數值格式做一些修正。將質量比分方程（1）寫成如下形式Y／t＋f／x－Yg／x＝0，其中f＝uY，g＝u。質量比分方程的半離散格式修正為：

在物質界面處，速度u保持常數，則離散格式（8）滿足壓力無振蕩的必要條件（7），且離散格式與質量比分方程（1）相容。

5 數值模擬

數值模擬用以檢驗格式的精度和性能，計算中一維算例CFL數取1.0，二維取0.5。

5.1 精度測試

在區域［0，2］上有兩種介質組成的正弦波：

周期邊界條件。表1中給出t＝1.0時各階格式精度測試結果，結果顯示2～5階格式都可以達到相應收斂率。

表1 格式的數值精度Table 1 Numerical accuracy of present schemes

5.2 一維多介質運動界面問題

在區域［0，1］上有兩種介質流體，以相同的速度勻速向右移動，界面勻速向右移動，初值條件為：

圖1顯示了采用守恒譜體積格式100個譜體積單元在t＝0.1時的壓力和速度，可以看出，在物質界面處出現速度與壓力的數值振蕩，與第3節中的分析結果一致。為方便看清圖像，圖中只顯示了奇數階結果。圖2顯示了格式修正后的計算結果，結果顯示，此時在物質界面處不會產生速度和壓力的數值振蕩，物質界面附近密度和比熱比的局部放大圖顯示高階格式具有更高的分辨率。

圖1 守恒譜體積格式的一維多介質運動界面問題Fig.1 One－dimensional moving interface problem for conservative spectral volume scheme

圖2 擬守恒譜體積格式的一維多介質運動界面問題Fig.2 One－dimensional moving interface problem for quasi－conservative spectral volume scheme

5.3 高壓力比氣液激波管問題

在區域［－0.2，1］上求解初值問題：

圖3顯式了t＝0.000 2時刻使用720個譜體積單元1、3、5階擬守恒譜體積格式計算的結果，結果顯示，此時在物質界面處不會產生速度和壓力的數值振蕩。圖4顯示了密度及其在物質界面和激波附近的局部放大圖，結果表明高階格式具有更高分辨率。

圖3 擬守恒譜體積格式的高壓力比氣液激波管問題Fig.3 High pressure ratio gas－liquid shock tube problem for quasi－conservative spectral volume scheme

圖4 擬守恒譜體積格式的高壓力比氣液激波管問題Fig.4 High pressure ratio gas－liquid shock tube problem for quasi－conservative spectral volume scheme

5.4 三點問題

初值條件為：

初始空氣（輕介質）位于水（重介質）上方，兩種介質流體保持靜止，靜止高密度高壓氣體位于其右側分別與低壓空氣和水產生作用，分別產生向左運動的稀疏波、向右移動的激波，以及推動物質界面向右移動。由于右側上方的空氣較輕，因此右側上方的激波和物質界面向右移動的速度更快，于是在3種狀態的流體的交匯點產生漩渦。形成漩渦后，上層空氣與下層水的交界面發生彎曲，并與激波發生作用，形成馬赫桿。圖5顯示了t＝1.0時使用600×200個網格2～5階格式計算的結果，可以看到，各階格式都能計算出此時基本的波結構，并且隨著格式精度的增加能夠捕捉到更精細的結構。

圖5 擬守恒譜體積格式的三點問題密度等值線圖Fig.5 Density contours of triple point problem for quasi－conservative spectral volume scheme

6 結 論

以多介質擬守恒格式為基礎，通過高精度譜體積重構，構造了一類求解多介質問題的高階精度擬守恒譜體積格式，有效提高了求解多介質問題的精度，并且繼承譜體積格式模板緊致、易于并行等優點。數值結果表明，新格式求解多介質問題具有高階精度，且模板緊致，并且不會在物質界面處產生非物理振蕩。

參考文獻：

［1］Abgrall R.How to prevent pressure oscillations in multicomponent flow calculation：A quasi conservative approach［J］.Journal of Computational Physics，1996，125（1）：150－160.

［2］Abgrall R，Karni S.Computations of compressible multifluids［J］.Journal of Computational Physics，2001，169（2）：594－623.

［3］Shyue K M.An effcient shock－capturing algorithm for compressible multicomponent problems［J］.Journal of Computational Physics，1998，142（1）：208－242.

［4］Shyue K M.A fluid－mixture type algorithm for compressible multicomponent flow with Mie－Gruneisen equation of state［J］.Journal of Computational Physics，2001，171（2）：678－707.

［5］Chen Y B，Jiang S.A non－oscillatory kinetic scheme for multicomponent flows with the equation of state for a stiffned gas［J］.Journal of Computational Mathematics，2011，29（6）：661－683.

［6］Johnsen E，Colonius T.Implementation of WENO schemes in compressible multicomponent flow problems［J］.Journal of Computational Physics，2006，219（2）：715－732.

［7］Zhu J，Qiu J X，Liu T G，et al.RKDG methods with WENO type limiters and conservative interfacial procedure for one－dimensional compressible multi－medium flow simulations［J］.Applied Numerical Mathematics，2011，61（4）：554－580.

［8］Wang Z J.Spectral（finite）volume method for conservation laws on unstructured grids：Basic formulation［J］.Journal of Computational Physics，2002，178（1）：210－251.

［9］Wang Z J，Liu Y.Spectral（finite）volume method for conservation laws on unstructured gridsⅢ：One dimensional systems and partition optimization［J］.Journal of Scientific Computing，2004，20（1）：137－157.

［10］Karni S.Multicomponent flow calculations by a consistent primitive algorithm［J］.Journal of Computational Physics，1994，112（1）：31－43.

High order spectral volume method for multi－component flows

Liu Na1，2，3，Chen Yibing1，3
（1.Institute of Applied Physics and Computational Mathematics，Beijing100088，China；2.CAEP Software Center for High Performance Numerical Simulation，Beijing100088，China；3.Laboratory of Computational Physics，Institute of Applied Physics and Computational Mathematics，Beijing100088，China）

Numerical simulation of multi－material flows has been an important issues in CFD，and most CFD production codes used for multi－material flow simulation is of either first or second order accuracy，too inefficient and costly with its grid refinement for high accuracy required problems.In this paper，a high－order，efficient，compact method，called the spectral volume method，was developed for the simulation of the multi－material flow as an extension of the spectral volume method for the conservation laws.It has been pointed out that the conservative spectral volume method for the multi－material flow will cause oscillation，and the reason for this has been analyzed.So the idea of quasi－conservative scheme was borrowed to prevent the spurious oscillations in the vicinity of a material contact discontinuity.Several numerical experiments proved that there is no oscillation near the material interface and the result also demonstrates the accuracy，the efficiency and the high performance of the scheme for the multi－material flow simulation.

fluid mechanics；spectral volume method；high order；stiffened gas；multi－component flows；compact stencil

O357.4國標學科代碼：1302511

A

10.11883／1001－1455（2017）01－0114－06

（責任編輯 丁 峰）

2015－05－11；

2015－09－20

國家自然科學基金項目（11101047，11501043，11671050，91430218，U1630247）；

中國工程物理研究院科學技術發展基金項目（2013A0202011）

劉 娜（1986— ），女，博士，助理研究員，liu＿na＠iapcm.ac.cn。