多智能體系統在切換拓撲和時變時延下的H∞一致性
覃 茜, 李慶奎
(山西大學 數學科學學院, 山西 太原 030006)
多智能體系統在切換拓撲和時變時延下的H∞一致性
覃 茜, 李慶奎*
(山西大學 數學科學學院, 山西 太原 030006)
研究了離散時間多智能體系統在切換拓撲和時變時延下的H∞一致性問題.考慮存在節點在一定時間內失聯且通訊可以恢復的情形,利用切換拓撲描述智能體間通訊鏈路的變化,并在有界時變時延和外部干擾下,將多智能體系統的H∞一致性問題轉化為切換H∞控制問題.提出一個僅基于智能體與其鄰居狀態信息的分布式一致性協議.基于此協議,在平均駐留時間切換機制下給出使得多智能體系統達到H∞一致性的充分條件.最后利用一個仿真例子驗證所提方法的有效性.
多智能體系統; 切換拓撲; 平均駐留時間;H∞一致性
0 引言
近幾十年來,多智能體系統因其在諸多領域的廣泛應用而吸引了來自國內外學者的關注,例如無人機的編隊飛行[1],車輛編隊控制[2],多機器人的協同控制[3],分布式傳感器網絡[4]等.一致性是多智能體系統中的一個典型問題,其主要研究如何設計分布式協議,使得所有智能體僅通過交換局部的狀態信息,最終達到一共同的狀態.一般地,將多智能體系統轉化為相應的誤差系統,其中誤差是每個智能體的狀態與最終一致狀態間的偏差,從而多智能體系統的一致性問題就轉變為誤差系統的穩定性問題[5].
在實際中,由于天氣,環境,自然災害(比如地震,暴雨雪)等因素,可能會導致智能體間通信鏈路的中斷,使得在某段時間內通信拓撲中可能會有孤立節點的存在,即某一智能體與其所有鄰居失去聯系.切換拓撲可用來刻畫通信鏈路的中斷和恢復,并且帶有切換拓撲的多智能體一致性已取得一定的成果[6,7].文獻[6]研究了速度約束的多智能體系統一致性,其假設并圖在每個時間區間都包含有向生成樹,但子拓撲的情況不明確.文獻[7]在分析帶有切換拓撲的一致性時則要求子拓撲是強連通的.雖然多智能體系統在切換拓撲下的一致性問題已被研究,但是鮮有針對節點失聯情形的一致性問題的探討,因此有必要對該問題展開討論.
通信拓撲的連通性對多智能體系統能否達到一致性至關重要,拓撲存在孤立點時是不連通的,這意味著多智能體系統在某些時間段內不能達到一致性,相應地,切換誤差系統包含有不可鎮定的子系統;由切換系統理論可知若不可鎮定子系統運行的總時間足夠小的話,整個切換系統還可以是穩定的[8].因此,設計合適的切換律使得系統在存在孤立點的情況下達到一致性是我們研究的另一個目的.
此外,智能體間的信息交換是以網絡為媒介的,在網絡環境下時延和外部干擾的存在不可避免,因此研究帶有時變時延和擾動的多智能體系統的一致性更加符合實際.基于此,本文研究了在時延和外部干擾下,多智能體系統在某些時間段內存在孤立節點的一致性,通過設計合適的一致性協議和切換律使其在包含不可一致子系統時依然能夠達到一致性;最后利用一個仿真例子驗證所提方法的有效性.
1 預備知識和建模
1.1 圖論
將每個智能體看作一個節點,用圖G={V,E,A} 來建構智能體間的通信拓撲,其中V={1,…,N}是N個智能體的集合,可被視作圖G的頂點集,i表示第i個智能體.邊集E?V×V且(j,i)∈E當且僅當i可向j發送信息,此時稱j是i的鄰居.i的鄰居節點集用Ni={j|j∈V,(j,i)∈E} 表示.若一個節點既沒有鄰居,同時又不是任何節點的鄰居,就稱其為一個孤立點.節點i1與ik間的一條有向路徑是一組以i1開始,ik結束的首尾相接的邊(i1,i2),(i2,i3),…,(ik-1,ik)∈E,若至少存在一個節點與其他任意節點間都有一條有向路徑,則稱該圖包含一個有向生成樹.用A=[αij]∈RN×N表示圖G的加權鄰接矩陣,且αij=1當且僅當(j,i)∈E,否則αij=0.在本文中我們假設沒有自環存在,即αii=0.圖G的拉普拉斯矩陣L=[lij]∈RN×N定義為
(1)
本文考慮了在某些時間段內有且只有一個節點與其他節點失去聯系,并隨后恢復通信,換句話說就是在短時間內通信拓撲中會存在一個孤立點.注意該孤立點不是固定的某一節點,會隨時間而變動,這意味著通信拓撲是隨時間變化的.用Gσ(k)表示時變的拓撲,其中σ:[0,∞)→M={0,1,…,N} 是切換信號,且σ(k)=m(m=1,…,N) 表示第m個智能體是孤立點,而σ(k)=0 表示在k時刻拓撲中沒有孤立點存在.圖集{Gσ(k):k∈[0,∞)}的并圖用Gun表示,其節點和邊分別是圖集中圖節點和邊的并.我們給出下面的假設以進行下面的討論.
假設1 圖Gun包含一個生成樹.
1.2 建模
考慮由N個智能體組成的多智能體系統,第i個智能體的動力學可描述為
xi(k+1)=Axi(k)+Bui(k)+ωi(k)
(2)
其中xi(k)∈Rn和ui(k)∈Rm分別是第i個智能體的狀態與控制輸入;ωi(k)=[0,…,0,ωin(k)]∈Rn是作用在i上的干擾;矩陣A和B為合適維數的常矩陣.

m

(3)
在切換拓撲下,對σ(k)=h,h∈M={0,1,…,N},分布式一致性協議給出如下
(4)
其中Kh是一個公共的分布式一致性增益;時變時延τ(k) 滿足0<τ1≤τ(k)≤τ2.
定義1[9]系統(2)在協議(3)下達到了一致性,若對任意的初始條件xi(0)∈Rn有下式成立:


(5)

(6)

且y(k)是被控輸出.顯然,誤差系統(6)的穩定性意味著多智能體系統(2)的一致性.
2 一致性分析
本文的研究目的是設計合適的一致性協議和切換律使得多智能體系統(2)達到一致性.首先給出下面的定義.
定義2[10]稱多智能體系統(2)達到了H∞一致性,若誤差系統(6)滿足
(1)在ω(k)=0時是指數穩定的,即
‖δ(k)‖≤ρe-λ(k-k0)‖δ(k0)‖;
(2)在零初始條件下,輸出y(k)對任意的ω(k)∈l2[0,∞)滿足
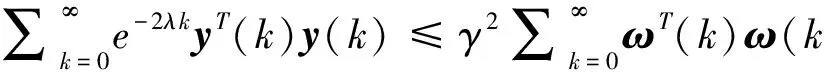
引理1[11]對任意的實矩陣W=WT>0和正標量r2≥r1≥0,下面的不等式成立

對相應于沒有孤立點和帶有一個孤立點情形的誤差系統,我們分別給出下面兩個重要的引理.
定義李雅普諾夫函數為
其中
η(s)=δ(s+1)-δ(s),τ12=τ2-τ1.

首先考慮沒有孤立點的情形,即當σ(k)=0時,誤差系統(6)描述為
(7)
選取李雅普諾夫函數
(8)
然后我們有下面的引理.

(9)
那么沿系統(7)的軌跡有下式成立
其中Γ(s)=δT(s)δ(s)-γ2ωT(s)ω(s)
φ0=[IN?A,-L0?BK0,0,0,Bo]

證明:令ξ(k)=[δT(k),δT(k-τ(k)),δT(k-τ1) ,δT(k-τ2),ωT(k)]T,通過計算容易得到
V0(k+1)-e-αV0(k)=


(10)
Θ1=diag{-e-αP0,0,0,0,0} ;

(11)
結合引理1有
(12)
令γ=diag{I,0,0,0,-γ2I},則Γ(s)可改寫為
Γ(s)=ξT(s)γξ(s)
(13)
聯合(10)~(12)以及(13),并令Ξ0=Θ1+Θ2+Θ3+γ有
V0(k+1)-e-αV0(k)+Γ(k)≤
顯然,利用Schur補引理可知(9)保證了
V0(k+1)-e-αV0(k)+Γ(k)≤0
遞推可得
V0(k)≤e-αV0(k-1)-Γ(k-1)≤…≤
接下來考慮有節點失聯情形,即σ(k)=j(j=1,…,N)時,系統為
(14)
此時選取李雅普諾夫函數
(15)
然后給出下面的引理.
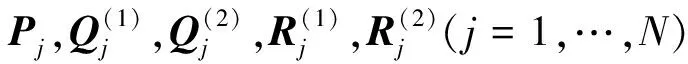
(16)
那么沿系統(14)有
其中Γ(s)=δT(s)δ(s)-γ2ωT(s)ω(s)
φj=[IN?A,-Lj?BKj,0,0,Bo]

證明:類似于引理2證明故而省略.
對一時間序列0=k0 定義3[12]對任意的T2>T1≥0,Nσ(T1,T2)表示在(T1,T2)內的切換次數;若對Ta>0和N0≥0有Nσ(T1,T2)≤N0+(T2-T1)/Ta,那么Ta稱為平均駐留時間,N0稱為抖振界.不失一般性N0選為0. (17) (18) 就稱多智能體系統(2)達到了一致性且具有H∞性能水平γ,其中μ≥1且滿足 (19) 證明:當ω(k)=0時,根據(19)有 V0(k)≤μVj(k),Vj(k)≤μμ′V0(k)(j=1,…,N) 由引理2-3可得 進而遞推得到 V(k)≤Vj(k2l+1)eβ(k-k2l+1)≤ μμ′V0(k2l)e-α(k2l+1-k2l)eβ(k-k2l+1)≤…≤ μNσ(k0,k)μ′N+(k0,k)V0(k0)e-α(k-k0-T+(k0,k))+βT+(k0,k) 注意N+(k0,k)≤(Nσ(k0,k)+1)/2并根據切換條件(17)和(18)可得 由(8)和(15)有下面的不等式成立 V(k)≥a‖δ(k)‖2,V0(k0)≤b‖δ(k0)‖2 其中 因此 當ω(k)≠0時,由引理2~3可得 遞推得到 (20) 在零初始條件下,由(20)可得 不等式兩邊同時從0到∞作和可得 這意味著誤差系統(6)在切換條件(17)和(18)下是指數穩定的并具有H∞性能水平γ,從而多智能體系統(2)達到了一致性. 考慮一個由3個智能體組成的多智能體系統,第i(i=1,2,3)個智能體的動力學為 ui(k)+ωi(k). 圖1給出了3個智能體間可能的交互拓撲,且相應的拉普拉斯矩陣如上式所示.其余系統參數給定如下: 基于上述參數,通過Schur補引理和合適的合同變換,利用MATLAB中的LMI和yalmip工具箱求解可得一致性增益 K0=[0.010 8 0.009 3] K1=[-0.003 9 0.004 0] K2=[-0.004 0 0.004 0] K3=[-0.004 0 0.004 2] 圖1 拓撲結構 計算得到T*=8.82,因此選取Tα=13.0和f+=0.11,則滿足條件(17)和(18)的切換信號在圖2中給出. 圖2 切換信號 系統初始狀態為x1(0)=[5;6]T,x2(0)=[2;3]T,x3(0)=[-5;-3]T,圖3的(a)和(b)展示了誤差系統的狀態變化.顯然由圖3可看出,多智能體系統(2)達到了一致性,驗證了所提方法的有效性. (a)誤差δi1的狀態響應 (b)誤差δi2的狀態響應圖3 誤差系統的狀態響應 本文研究了多智能體系統在時延和外部干擾下的H∞一致性.對于存在節點失聯的情形,利用切換拓撲描述通訊的中斷與恢復,并設計合適的分布式一致性協議和基于平均駐留時間機制的切換律,使得整個多智能體系統在包含有不可一致的子系統時最終仍能達到一致性.隨機時延與隨機切換是更加貼近實際的,可作為未來的研究方向. [1] Abdessameud A,Tayebi A.Formation control of VTOL unmanned aerial vehicles with communication delays[J].Automatica,2011,47(11):2 383-2 394. [2] Ren W.Decentralization of virtual structures in formation control of multiple vehicle systems via consensus strategies[J].European Journal of Control,2008,14(2):93-103. [3] Sheng W,Yang Q,Tan J,et al.Distributed multirobot coordination in area exploration[J].Robotics & Autonomous Systems,2006,54(12):945-955. [4] Jayaweera S K.V-Blast-Based virtual MIMO for distributed wireless sensor networks[J].IEEE Transactions on Communications,2007,55(10):1 867-1 872. [5] Olfati Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1 520-1 533. [6] Lin P,Ren W,Gao H.Distributed velocity-constrained consensus of second-order multi-agent systems with switching topologies and delays[C]//Proceedings of the American Control Conference.Washington DC:IEEE Conference Publications,2013:540-545. [7] Wen G,Hu G,Yu W,et al.Distributed consensus of higher order multi-agent systems with switching topologies[J].IEEE Transactions on Circuits & Systems II Express Briefs,2014,61:359-363. [8] Sun X M,Liu G P,Wang W,et al. Gain of systems with input delays and controller temporary failure:Zero-order hold model[J].IEEE Transactions on Control Systems Technology,2011,19(3):699-706. [9] Ren W,Beard R W.Consensus seeking in multi-agent systems under dynamically changing interaction topologies[J].IEEE Transactions on Automatic Control,2005,50(5):655-661. [10] Lin P,Jia Y.Robust H∞ consensus analysis of a class of second order multi-agent systems with uncertainty[J].IET Control Theory & Applications,2010,4(3):487-498. [11] Zhang D,Yu L,Zhang W A.Delay-dependent fault detection for switched linear systems with time-varying delays the average dwell time approach[J].Signal Processing,2011,91(4):832-840. [12] Liberzon D.Switching in systems and control[M].Boston:Birkh?user Boston,2003. 【責任編輯:陳 佳】 H∞consensus for multi-agent systems with switching topologies and time-varying delays TAN Xi, LI Qing-kui* (School of Mathematical Sciences, Shanxi University, Taiyuan 030006, China) We investigate the problem ofH∞consensus for the multi-agent systems with switching topologies and time-varying delays.Consider the case that there exists an unspecified node loses connection with others in some time periods and the communication links can be restored,switching topologies are used to construct the communication among agents,and in the presence of bounded time-varying delays and external disturbance,theH∞consensus problem can be transformed into a switchedH∞control problem.Then a distributed consensus protocol based on the state information of the agent and its neighbors is proposed to achieve theH∞consensus.Based on this protocol,sufficient conditions are proposed under an average dwell time switching scheme such that the whole multi-agent system reaches theH∞consensus.Lastly,a simulation example is presented to verify the effectiveness of the proposed methods. multi-agent system; switching topologies; average dwell time;H∞consensus 2016-12-28 基金項目:國家自然科學基金項目(6157020879); 山西省回國留學人員科研資助項目(2015-017) 覃 茜(1991-),女,山西呂梁人,在讀碩士研究生,研究方向:切換時滯系統、網絡控制系統 李慶奎(1971-),男,山東郯城人,副教授,博士,研究方向:切換時滯系統、網絡控制系統,sdlqk01@sxu.edu.cn 1000-5811(2017)02-0183-06 TP13 A








3 仿真





4 結論

