一種改進的不確定性水質模型參數率定方法

張質明,王曉燕,潘潤澤(1.首都師范大學資源環境與旅游學院,北京 100048；.北京建筑大學環境與能源工程學院,北京應對氣候變化研究和人才培養基地,城市雨水系統與水環境教育部重點實驗室,北京 100044)

一種改進的不確定性水質模型參數率定方法

張質明1,2,王曉燕1*,潘潤澤2(1.首都師范大學資源環境與旅游學院,北京 100048；2.北京建筑大學環境與能源工程學院,北京應對氣候變化研究和人才培養基地,城市雨水系統與水環境教育部重點實驗室,北京 100044)

為了能夠使得水質模型的參數率定更符合實際情況,減少水質模型當中常出現的異參同效的現象,提出一種能夠結合實驗與算法共同對模型參數進行識別的方法,即通過設置約束條件,將單純的“與實測值進行對比”的一般率定過程轉化為"能夠對模型內部過程進行一定程度控制"的率定過程.以WASP模型在北運河的某河段中進行的水質模擬結果表明,通過引入約束條件可以從更為系統的角度有效地去除部分不符合污染物轉化規律的參數組合,使得最終水質模型能夠更為準確地反映實際的水質變化過程,同時也減少了模型的不確定性與模型參數率定的“異參同效”現象;在模型的非線性結構與約束條件的作用下,相同子模塊中原本獨立的參數會呈現一定的相關性;隨著對區域的水質變化過程研究的深入,當引入新增約束條件或是降低容錯比例時,約束條件的作用將會進一步增強.

水質模型；約束條件；參數率定；異參同效

當前水質模型成為水環境定量化管理中的重要工具,如WASP、QUAL2K、MIKE等復雜的機理模型在各類水體中得到了大量應用.為了使得機理模型能夠更為詳細地體現水體中污染物的遷移轉化的過程,模型內部的結構復雜程度顯著提升,參數的率定的難度也隨之增加.

為了解決模型的參數率定問題,許多方法也隨著計算機技術的發展而大量涌現,目前較為常見的若干參數率定方法包括:遺傳算法、模擬退火算法、粒子群算法[1]、GLUE方法等以及各類方法所衍生出來的修正算法[2-4].

然而這類依靠似然函數進行率定的方法無法很好地解決復雜模型中的“異參同效”的問題.盡管機理模型具備理論概念的框架,但由于率定的似然函數僅僅針對觀測值與最終模型的輸出結果,忽視了對模型內部運算過程的驗證,當多個參數組合的似然度近似,便無法判斷參數取值的正確性.雖然這種現象可以通過大量的歷史實測數據的驗證來進行緩解,但由于水質監測的成本非常高[5-6],許多地方的監測投入不足或是由于歷史數據缺失嚴重,很大程度上影響了模型在研究區域的可行性.

在模型的實際應用中,由于用于率定的實測數據本身具有不確定性,即使提供很長的時間序列以供模型的驗證,也需要考慮這段時期是否具有代表性.當環境因外界原因(如污染源、水力條件等)產生較大程度變化時,用于描述機理的參數取值也不應是固定不變的.而如果忽視這個問題,進而通過機器算法不斷調整參數,迫使模擬值不斷逼近帶有不確定性的實測值,就有可能會出現一些不合理的參數組合.實際上,水質模型參數取值的準確與否,不僅需要讓最終模擬結果與實測值具有較高似然度,同時也應在模擬過程中體現水質變化的實際規律.

由于水環境模型參數的取值準確性非常關鍵,一些研究者直接采用實驗方法對敏感關鍵參數進行測定,用于研究區的水質模擬[7-9];同時,利用實驗室模擬的結果,也可以對模型的結構進行改進[10].當實驗條件設計合理時,這類通過實驗測定的參數的方法比通過計算機算法率定所得到的參數更準確,但這種針對特定參數的獲取方法往往成本較高.此外,在具有復雜結構的模型中,能夠直接測定的參數并不多.

為了在參數率定當中既能夠較好兼顧實驗室模擬的針對性與機器率定方法的效率,本文以WASP模型在北運河的某河段中模擬氮的轉化為例,提出一種能夠結合實驗與算法共同對模型參數進行識別的方法.不同于直接測定特定參數,而是利用實驗結果作為“約束條件”,既可以節約成本,也為引入相同研究區的其他研究結果提供了可能性,并且該方法避免了因“異參同效”所導致的問題,在很大程度上提高模型的率定的準確程度.

1 數據與方法

1.1 研究區域概況

選用北運河中一段水力條件與污染物匯入狀況均較為簡單的河段進行模擬,該河段總長約30km.數據采用課題組在2009年4月～10月(模型率定期)及2010年的4、7、10、12月(驗證期)的非降雨時段對榆林莊至楊家洼閘段(圖2)的河道流量及水質(包括COD、CBOD、氨氮、硝態氮、DO、鹽度、葉綠素、pH、水溫等指標)的同步監測成果.

該河段地勢平緩,流速緩慢(約0.01～0.5m/s),河段狹長,沒有支流及取排水口對河道水量的干擾,且沿河水力狀況變化較小,流經區域主要為農地、林草地,主要污染來自面源,在沒有降雨的時段,基本可以視為沒有外源匯入,邊界條件相對簡單.

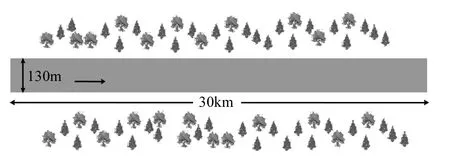
圖1 采樣點空間分布與河道概化Fig.1 Location of monitoring sites of North Canal in Tongzhou

1.2 EUTRO模塊

WASP模型中的EUTRO模塊可以用來模擬常規污染物的遷移轉化.該河段水質受氮污染的影響嚴重,因此本文采用其中的關于 CBOD、DO、氨氮、硝態氮等主要模塊來進行該河段污染物降解的模擬.由于WASP模型的封裝性,僅能觀測到某項指標模擬的總體結果,因此本文基于MATLAB環境下利用Simulink對該模塊進行了拆分,便于觀測各部分的計算結果.

各項指標的計算過程如下,其中各項參數及變量的意義詳見WASP模型的手冊:

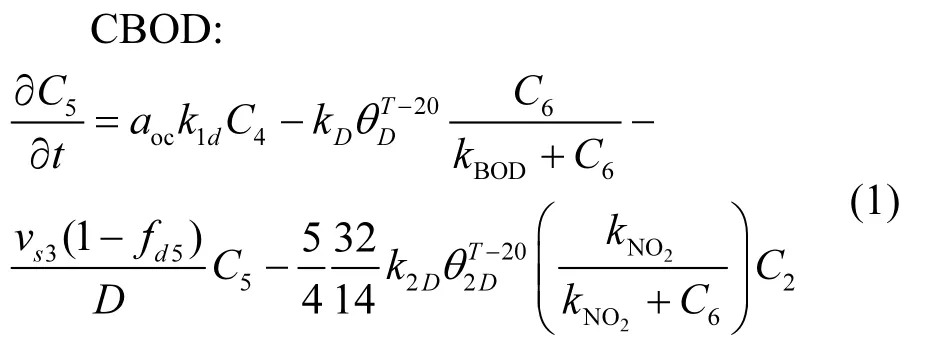
式中:第1項為浮游植物的死亡、第2項為CBOD的氧化、第3項為CBOD的沉淀、第4項為反硝化作用.

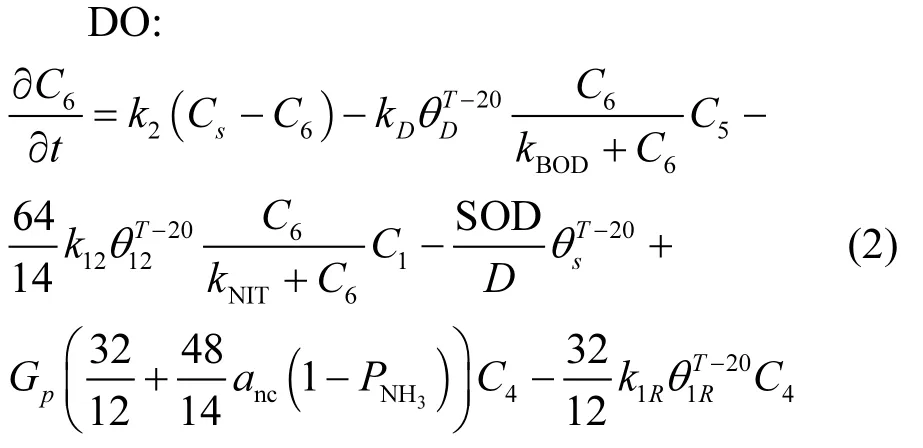
式中:第1項為大氣復氧、第2項為因CBOD的氧化作用(碳化作用)、第3項為硝化作用、第4項為底泥耗氧、第5項為水生植物生長(光合作用)、第6項為水生植物的呼吸作用.

氨氮:

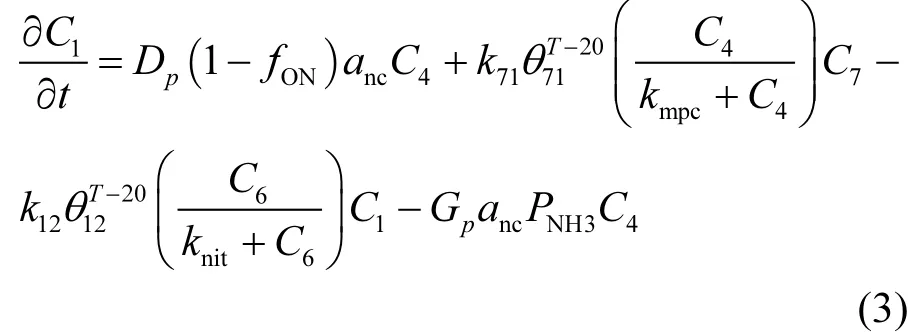
式中:第1項為水生植物死亡、第2項為礦化作用、第3項為水生植物生長、第4項氨氮硝化作用.

硝態氮:

式中:第1項為硝化作用、第2項為水生植物生長、第3項為反硝化作用.

1.2.1 率定方法 EUTRO當中涉及的水質指標轉化過程比較多,不能通過實驗方法一一進行測定.但由于參數所描述的水質變化過程應當遵循研究區域的水質變化的特征,與實驗室模擬當中獲取的結果不應差異過大.此外由于水環境作為一個開放系統,水體在自凈過程中受到許多來自于人為、自然的外界干擾作用,因此在模型參數取值的選擇上也應當考慮不確定性,大部分常值參數(除分子量比之類的具有確切值的參數以外)均應該考慮在一定范圍內的變化所造成的影響.

在諸多率定方法中,GLUE算法將模型參數的分布狀況替代了單一參數的取值[11-13],在模型不確定性的研究中得到了大量的應用[14-16].由于GLUE方法所借鑒的貝葉斯理論,是將前一次模擬得到的參數后驗分布作為第 2次模擬時的先驗分布.可以不斷增加估計參數的信息,從而率定出最優的參數組合范圍.每組隨機生成的參數對應一個似然值,需要借助一個準則來判斷是否接受這組參數.在本研究中,參數的范圍根據先前的研究來確定,參數組合的抽樣通過拉丁超立方的方式進行選取,經過模擬后,篩選出似然值最高的5%的參數組合,作為可被接受的參數集.

1.2.2 條件約束 由于北運河的氮污染物排放強度大,水體中的氮污染遠遠高于國外河流,因此其污染物的遷移轉化也具有一定的特殊性,參數的本土化就顯得非常重要.而在許多模型率定的研究中,參數的先驗分布往往借鑒其他研究案例或者默認值來選取,其合理性有待商榷.為了能夠對參數更好地進行本土化,本研究在率定之前,全部的參數需要經過約束條件進行初篩.在約束條件與模型兩者的作用下,參數的初始分布會由均勻分布產生了改變,并且這些參數相互之間的獨立性也可能因此而消失.

本研究利用課題組2008年5～8月在北運河沙河閘與楊洼閘采樣,通過實驗室模擬測定所獲得的結果[17],作為條件來對模型參數的率定過程進行約束.這樣可以保障參數取值的本地化.

如前所述,WASP模型當中的EUTRO模塊將BOD的耗氧過程分為CBOD與NBOD兩個部分,因此結合模型的結構特征,約束條件主要考慮以下3方面的內容.

(1) CBOD與NBOD比例

在采用羅威邦測定儀(德國),將水樣加入到帶有磁力攪拌器的棕色培養瓶中,在20℃條件下培養 10d,記錄每天的值.通過對比加與不加丙烯基硫脲(ATU,用于抑制氨氧化細菌的活性)的 2組水樣,其濃度差值就是NBOD,每組設置3個平行樣,結果取其濃度的平均值.

根據測定結果,楊洼閘的CBOD與NBOD的平均耗氧量之比為18.25/23.79.然而,一方面該取值在自然環境下會受到外界因素干擾,應該只在一定程度上具有參考性;另一方面,作為約束條件,應當適當放寬范圍,以便參數抽樣的結果能夠落在區間內,而非一個確切的點上.由于上游沙河閘的CBOD與NBOD的平均耗氧量之比為16.65/ 20.33,同時考慮到沿途排污口匯入時的干擾,變化范圍約為 10%～15%,因此本研究設定相應容許范圍為±15%,得到約束條件:

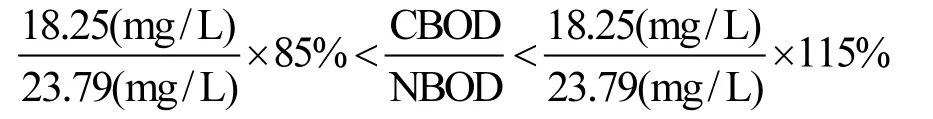
式中:CBOD為 BOD中碳化部分消耗的氧量, NBOD為硝化部分消耗的氧量.

有機物質的生物化學氧化反應一般分為兩個階段,第一階段為碳氫化合物氧化為二氧化碳和水,稱為碳化階段;第二階段氨被氧化為亞硝酸鹽及硝酸鹽,稱為硝化階段.在EUTRO模塊當中,這兩部分的耗氧分別對應溶氧模擬中的碳化與硝化兩部分.其中,在碳化部分的計算,模型采用以 CBOD、溶解氧、溫度的函數來實現,而關于硝化部分的耗氧量則通過氨氮、溶解氧、溫度的函數來實現.

(2) 氨氮的降解速率

氨氮的降解系數可以通過模型模擬出來的氨氮變化速率來得到.在模型中,影響氨氮濃度的環節包括浮游植物的死亡/內源呼吸、礦化作用、浮游植物的生長、以及硝化作用4個環節的共同作用.作為氨氮變化其中的一個過程,硝化活性的衡量可通過 EUTRO中硝化過程對于氨氮衰減量的貢獻來進行模擬.

根據對北運河氨氮降解系數的測定實驗結果,該榆林莊橋至楊洼閘斷面的氨氮降解系數為0.0089～0.1012/d.該實驗是在自然條件下對水中氨氮的濃度進行連續監測得到的范圍,因此在模型模擬時,該模塊降解的量不應低于原來濃度的0.89%,且不應高于10.12%.根據北運河氨氮的濃度現狀(北運河氨氮濃度為 10.1～23.3mg/L),限定其變化范圍為:

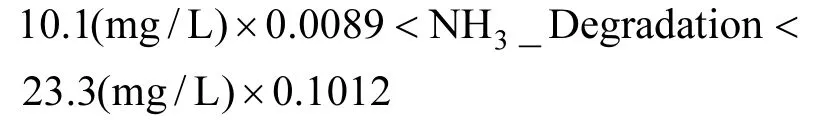
其中:NH3_Degradation代表氨氮在單位時間內的降解量.

(3) 硝化活性

硝化過程是河流系統中氮循環的一個重要環節.通過硝化過程,氨氮轉化為硝態氮與亞硝態氮,其速率反映了河流對氨氮降解過程的效率[18].經過對氨氧化過程和抑制氨氧化過程中硝化產物NO2

-和NO3-濃度變化情況可計算得到研究區水體的硝化活性范圍為在0.24～4.29mg/(L?d).

在 EUTRO模型中,計算氨氮變化量的第四項為氨氮向的氮氧化物轉化過程的模塊.該模塊的計算結果反映了模擬對象水體的氨氮濃度變化速度.

2 結果與討論

2.1 可行參數約束結果

根據實驗結果對參數集可行域范圍的劃定,可以發現一些參數的先驗范圍發生了變化.由于約束條件的存在,原本相互獨立的參數取值呈現了一些相關性.例如圖2中所示,參數ED的取值與參數 KD的取值就明顯受到了約束條件的影響.這是由于ED與KD 2個參數同屬氧化過程的模擬環節,該環節對本研究涉及到的約束條件都有顯著的機理關系,因此約束的結果較為明顯.在參數抽樣環節中,對于存在強相關性的參數,不應逐一取值,而是應當考慮在篩選的參數組集合當中進行選取,以免出現錯誤的組合.

事實上,在水質模型中,污染物遷移轉化規律的描述常常需要通過多個參數才能夠完成.因此參數組合的確定十分重要,如果對先驗參數不進行篩選,而直接進行獨立取值,許多不合理的參數組合將可能出現,顯然這些參數組合會歪曲真實的模擬過程.而這種錯誤在模型的應用中有時很難被發現:一方面,用于評估模型效果的似然度往往通過人為設定的似然函數進行計算而得到,而復雜模型當中“過擬合”或“同效”的現象可能會使得一些似然度看起來很高,但事實上是由不合理的參數組合所形成的“最優解”;另一方面,似然函數的計算往往只針對最終的模擬結果與實測值的對比,而非基于過程進行監控,對于里面子模塊的響應正確與否無從驗證.例如,本研究當中的氨氮模擬分為四項:水生植物死亡、礦化作用、水生植物生長、氨氮硝化,這4項的增減都會影響到最終氨氮濃度的大小.顯然,如果不對子模塊的響應進行驗證,每個子模塊響應的不確定性則會較大,在“同效”現象存在時,就很難識別出氨氮增減的真正原因.

當將約束條件介入參數的選取時,不符合條件的參數組合會被舍棄.因此,即便這部分參數當中某些參數組合的似然度較高,也仍然不會被選擇,從而減少模擬錯誤的可能性.隨著約束條件的增加,可被篩選的參數組合的數量也會降低,因“同效”現象導致的錯誤也會隨之減少.

在本研究中,通過約束條件來確定先驗分布,會改變初始參數組合,在篩除一部分參數組合的同時,也可以在一定程度上減少因"異參同效"而引起的對污染物轉化機理模擬的偏差.除了對參數初始范圍的影響外,約束條件可能還會在更高維度的空間對參數的分布進行改變,但這難以通過圖示對比看到,為了簡單示意,圖中僅展示了部分參數的二維分布,可以看到通過依據實測結果的篩選,這些參數的可行范圍以及參數的分布情況發生了一定的變化.如圖所示:落在淺色點覆蓋范圍內的任意一組組合都滿足參數約束條件中所歸定的規則,可視為符合北運河實測結果;而落在淺色點覆蓋區域之外的部分,盡管其符合單個參數的選取范圍(黑色區域),但與北運河的研究結果反映出來的水質轉化規律相矛盾,將會在之后的率定過程中舍棄.在本研究中,經過約束條件篩選出來的參數大約占原樣本的 1/5,這與本研究所采用的容錯范圍,約束條件的種類都有很大關系.毫無疑問,隨著約束條件的增加,滿足約束條件的參數樣本會進一步減少.

2.2 模型率定結果

將符合約束條件的參數組合作為先驗參數組,利用GLUE方法,對模型的參數取值進行率定.根據 WASP模型的敏感性分析研究篩選出來的10個最為敏感的參數[19]的率定值如圖 3所示.

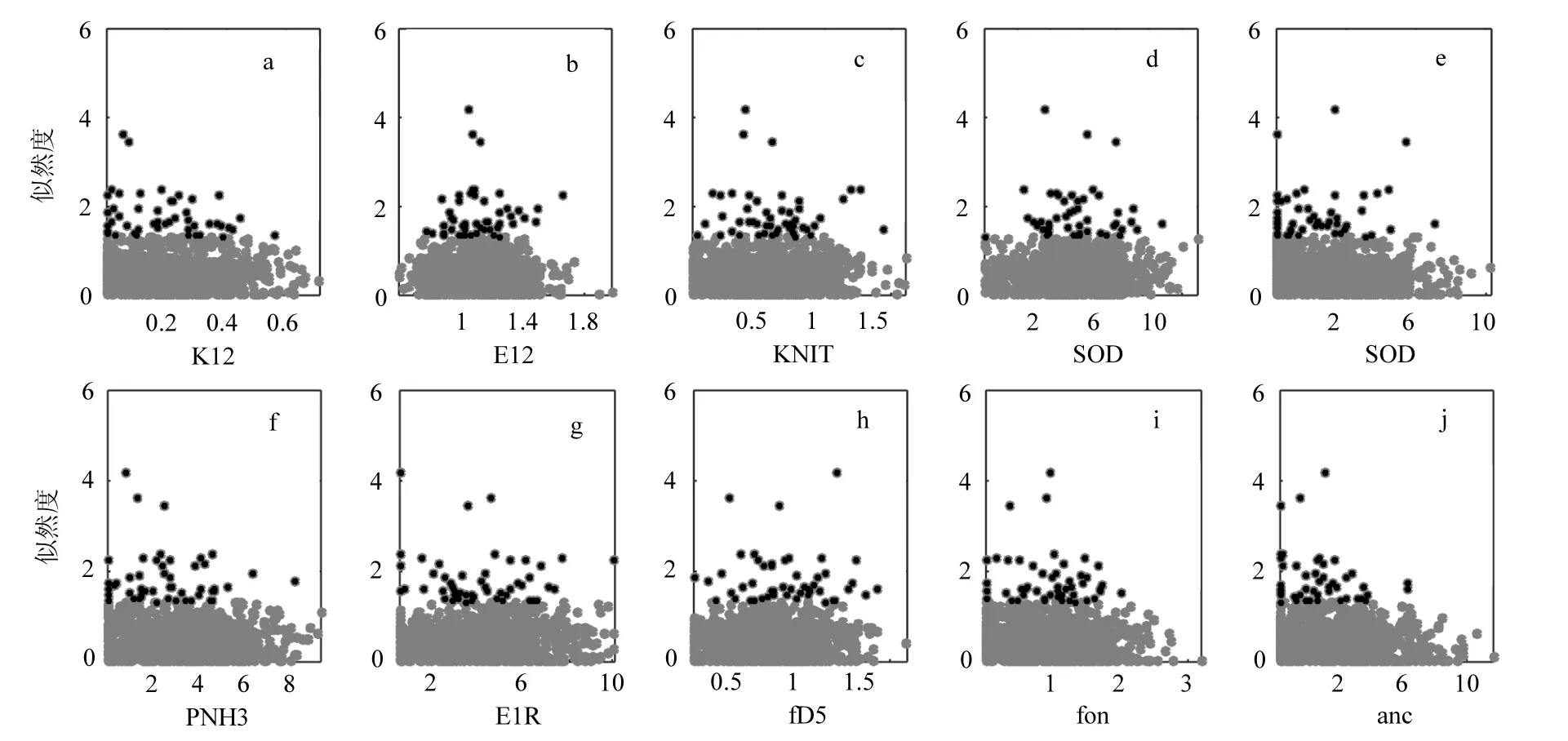
圖3 GLUE算法對模型主要敏感參數的篩選結果Fig.3 Calibration of main sensitive parameters combination by GLUE algorithm

可以看出,經過模型參數的約束,一些模型參數在似然度較高的部分出現了較為明顯的集中.盡管有一些參數仍然不能很好地通過 GLUE方法進行識別,這是由于實測數據數量較少或者模型本身概化所致,說明在這些參數當中"異參同效"的現象比較明顯.

一般來說,GLUE方法的一個重要思想是強調參數組合對模擬結果的影響.但是目前 GLUE方法也是基于對模擬結果與實測值之間的似然度來進行參數組合的篩選,當實測數據不足,或是其中一部分數據缺乏代表性,就會在很大程度上干擾到最終所選取的參數組合.而本研究將部分已知的研究區的水質轉化規律作為約束條件,把原本主觀的先驗分布轉變為經過篩選的參數組合,從另一個角度確保參數組合在描述水質轉化過程中的可靠性.這樣率定出來的結果既可以保證對最終結果的擬合效果,也能夠同時兼顧對水質轉化過程的控制.

3 結論

3.1 傳統的通過抽樣方法獲取的參數組合往往存在大量不符合污染物轉化規律的情況,通過引入約束條件可以從更為系統的角度有效地去除部分不符合污染物轉化規律的參數組合,使得最終水質模型能夠更為準確地反映實際的水質變化過程,同時也因此減少了模型的不確定性與模型參數率定的"異參同效"現象;

3.2 本研究總結了CBOD與NBOD比例、氨氮的降解速率與硝化活性等三個在研究區河段進行研究的成果,作為篩選合理參數的約束條件.在模型的非線性結構與約束條件的作用下,相同子模塊中原本獨立的參數會呈現一定的相關性;

3.3 在本研究中,符合約束條件的參數集合約為原樣本量的 1/5.隨著對區域的水質變化過程研究的深入,當引入新增約束條件或是降低容錯比例時,這一比例還會進一步降低.

[1] 劉蘇寧,甘 泓,魏國孝.粒子群算法在新安江模型參數率定中的應用 [J]. 水利學報, 2010,(5):537-544.

[2] 郭建青,李 彥,王洪勝,等.應用單純形-模擬退火混合算法估計河流水質參數 [J]. 水科學進展, 2004,(6):765-769.

[3] 王綱勝,夏 軍,陳軍鋒.模型多參數靈敏度與不確定性分析 [J].地理研究, 2010,(2):263-270.

[4] 劉 毅,陳吉寧,杜鵬飛.環境模型參數優化方法的比較 [J]. 環境科學, 2002,(2):1-6.

[5] Mannina G, Viviani G. Water quality modelling for ephemeral rivers: Model development and parameter assessment [J]. Journal of Hydrology, 2010,393(3/4):186-196.

[6] Naddeo V. River water quality assessment: Implementation of non-parametric tests for sampling frequency optimization [J]. Land Use Policy, 2013,30(1):197-205.

[7] Raimonet M, L Vilmin, N Flipo, et al. Modelling the fate of nitrite in an urbanized river using experimentally obtained nitrifier growth parameters [J]. Water Research, 2015,73:373–387.

[8] 逄 勇,丁 玲,高 光.基于生態槽實驗的藻類生長參數確定[J]. 環境科學, 2005,(3):78-82.

[9] 歐陽威,蔡冠清,黃浩波,等.基于原位土壤觀測的 SWAT關鍵參數及模擬優化分析 [J]. 農業環境科學學報, 2014,(8):1601-1608.

[10] 王飛兒,楊 佳,李亞男,等.基于沉積物磷釋放的 WASP水質模型改進研究 [J]. 環境科學學報, 2013,(12):3301-3308.

[11] Arhonditsis G B, Qian S S, Stow C A, et al. Eutrophication risk assessment using Bayesian calibration of process-based models: Application to a mesotrophic lake [J]. Ecological Modelling, 2007,208(2–4):215-229.

[12] Missaghi S, Hondzo M. Evaluation and application of a three-dimensional water quality model in a shallow lake with complex morphometry [J]. Ecological Modelling, 2010,221(11): 1512–1525.

[13] Zhang W, Arhonditsis G B. A Bayesian hierarchical framework for calibrating aquatic biogeochemical models [J]. Ecological Modelling, 2009,220(220):2142-2161.

[14] Beven K, Freer J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology [J]. Journal of Hydrology, 2001,249(1–4):11-29.

[15] Liu Y, P Yang, C Hu, et al. Water quality modeling for load reduction under uncertainty: A Bayesian approach [J]. Water Research, 2008,42(13):3305-3314.

[16] Ratto M, Tarantola S, Saltelli A. Sensitivity analysis in model calibration: GSA-GLUE approach [J]. Computer Physics Communications, 2001,136(3):212-224.

[17] 于 洋.北運河水體中氨氮的氧化過程及微生物響應特征 [D]. 2012.首都師范大學.

[18] 王 超,單保慶,趙 鈺.滏陽河水系沉積物硝化速率分布及溶解氧的限制效應 [J]. 環境科學學報, 2015,35(6):1735-1740.

[19] 張質明,王曉燕,李明濤.基于全局敏感性分析方法的 WASP模型不確定性分析 [J]. 中國環境科學, 2014,34(5):1336-1346.

A parameter calibration method with constraint based on laboratory experimental result.

ZHANG Zhi-ming1,2,WANG Xiao-yan1*, PAN Run-ze2(1.College of Resources, Environment and Tourism, Capital Normal University, Beijing 100048, China；2.Beijing Climate Change Response Research and Education Center, Beijing University of Civil Engineering and Architecture, Beijing 100044, China). China Environmental Science, 2017,37(3)：956～962

In order to make the parameters of the water quality model more realistic and reduce the equivalent phenomenon of different parameters in water quality model, this paper proposed a method to identify the model parameters by setting laboratory experimental constraints, which could be used to make a certain degree of internal process control. The example of a water quality simulation by WASP model in a section of the North Canal showed that by this method, the model could be more accurate to reflect the actual water quality change process by reducing uncertainty and equivalent from combination of the parameters. Through the action of the nonlinear model structure and constraint conditions, the originally independent parameters under the same sub module began to demonstrate certain correlation. With the further study of the water quality change process, the constraint conditions would be further enhanced when introduced new constraint conditions or fault decrease tolerance.

water quality model；constraint；parameter calibration；equivalent

X703

A

1000-6923(2017)03-0956-07

張質明(1984-),北京人,講師,博士,主要研究方向為水環境模擬.發表論文10余篇.

2016-07-01

北京市自然科學基金青年項目(8154044);國家自然科學基金項目(41271495);高等學校博士學科點專項科研基金聯合資助項目(20121108110006)

* 責任作者, 教授, cnuwxy@sohu.com