考慮溫度影響的飽和軟黏土應變軟化研究

范思婷， 劉干斌， 陳 斌， 葉俊能

(1. 寧波大學 巖土工程研究所, 寧波 315211; 2. 寧波市軌道交通工程建設指揮部, 寧波 315010 )

考慮溫度影響的飽和軟黏土應變軟化研究

范思婷1， 劉干斌1， 陳 斌2， 葉俊能2

(1. 寧波大學 巖土工程研究所, 寧波 315211; 2. 寧波市軌道交通工程建設指揮部, 寧波 315010 )

循環荷載作用下飽和軟黏土將產生應變軟化現象，通過對寧波飽和軟黏土開展溫控動三軸試驗，研究了溫度、頻率、初始偏應力、動應力和含水率對土體應變軟化的影響，并在試驗基礎上建立了一個能夠考慮溫度影響的應變軟化模型。結果表明：隨著振動次數、初始偏應力、動應力和含水率的增加，土體軟化加快，軟化指數逐漸減小；隨著頻率和溫度的提高，土體軟化程度降低，軟化指數增大；建立的軟化模型可以較為合理地描述試驗溫度、頻率、初始偏應力、動應力和含水率對土體應變軟化特性的影響。

溫控動三軸試驗；溫度荷載；應變軟化；軟化指數

在交通、波浪等循環荷載作用下，地基土體表現出軟化特性，其中循環應力比、超固結比、主應力方向、應變速率、振動頻率等因素對土體軟化影響較大[1-4]。IDRISS等[5]首先采用“軟化指數”來描述循環荷載下土的軟化特性，并建立了軟化指數與循環次數間的關系式。此后，YASUHARA等[6]通過類似的方法得到了軟化指數與循環次數之間的半對數關系表達式。周建等[7]對土的軟化原因進行了總結，認為循環荷載作用下飽和軟黏土中的孔壓、主應力方向不斷改變、土的結構變化引起土體剛度、強度軟化，導致土體結構破壞，并研究了循環應力比、超固結比、加荷頻率對軟化指數的影響，建立了一個軟化模型。王軍等[8]考慮土體各項異性固結和高頻循環荷載方式，研究了循環次數、應力比、固結比、頻率、超固結比、初始偏應力對杭州飽和軟黏土應變軟化的影響。蔡袁強等[9]對杭州飽和軟黏土各向異性固結下的軟化特性及殘余應變發展規律進行了研究，并結合殘余應變-軟化模型對Iwan模型進行了修正。

近年來，在核廢料處理、熱管線埋設、公共交通系統等領域，溫度對土體力學性質的影響受到越來越多的關注。如在城市軌道交通運營中，地鐵列車長期往復運行產生大量熱量，向隧道維護結構和周圍土體(統稱“圍巖”)擴散。據對北京地鐵的估計[10]，圍巖傳熱量約占整個地鐵系統產熱量的25%～40%；紐約交通署公布的數據[11]表明整個地鐵系統運行時產生的熱量使得隧道以及站臺的溫度高于外界溫度8～10℃，夏天隧道內測得的溫度大部分都超過37℃。因此，開展不同溫度下的土體動力特性研究有很重要的工程背景和研究意義。

在負溫下，羅飛等[12]對青藏凍結黏土開展了循環荷載作用的動三軸試驗研究，探討了不同加載頻率、圍壓和負溫條件下的動應變幅值變化。在常溫下，楊果林等[13]通過對新型加筋土擋墻施加不同頻率、振幅的動變循環荷載，研究了動荷載作用下擋墻側向和豎向變形的發展變化規律；冷伍明等[14]利用動三軸試驗系統進行了振動荷載作用下粗顆粒土填料的臨界動應力試驗研究。在高溫下，朱遠武等[15]通過現場爆炸試驗，展開了爆炸作用下淤泥質軟土的熱力響應試驗研究，為沿海軟土地區地下人防工程設計和地基壓密處理提供了參考。劉干斌等[16]通過設計內外聯合加熱溫控裝置，研制了溫控動三軸試驗系統，開展了不同溫度下淤泥質軟黏土的動力特性試驗。

目前，循環荷載作用下土的應變軟化方面的研究較為深入，而對于不同溫度下土的應變軟化特性尚未有報道。為此，利用溫控動三軸試驗系統，本文開展了寧波飽和軟黏土的應變軟化試驗，研究了溫度、振動次數、頻率、動應力、初始偏應力和含水率等因素對土體應變軟化的影響，并建立了考慮溫度影響的土體應變軟化數學模型。

1 土的應變軟化試驗

1.1 土的應變特性

利用溫控動三軸試驗系統，對寧波軟黏土進行固結不排水動三軸試驗，土的基本物理力學指標見表1。

表1 土樣基本物理力學指標Tab. 1 Properties of soil sample

試驗方案如表2所示，試驗過程的排水固結、溫度控制與文獻[16]相同。考慮寧波軟土地層的沉積特性，各土層靜止土壓力系數主要在0.4～0.7之間，試驗中選擇k0(k0<0=0.7)固結和各向等壓固結兩種工況。由于實際工程中通常采用雙幅循環應變值(5%或10%)或者采用單幅循環應變與殘余累積應變之和(15%或20%)作為破壞標準[17]。結合寧波軟黏土的特點，本文以軸向累積應變達到5%作為破壞標準。參考寧波軌道交通列車荷載運行情況，最高運行速度為80 km/h，車輛長度約為20 m，計算得到振動頻率為1.11 Hz，因此，試驗中的振動頻率設為0.6 Hz、1 Hz、2 Hz，試驗目標溫度設定為25 ℃、35 ℃、45 ℃、55 ℃、65 ℃。

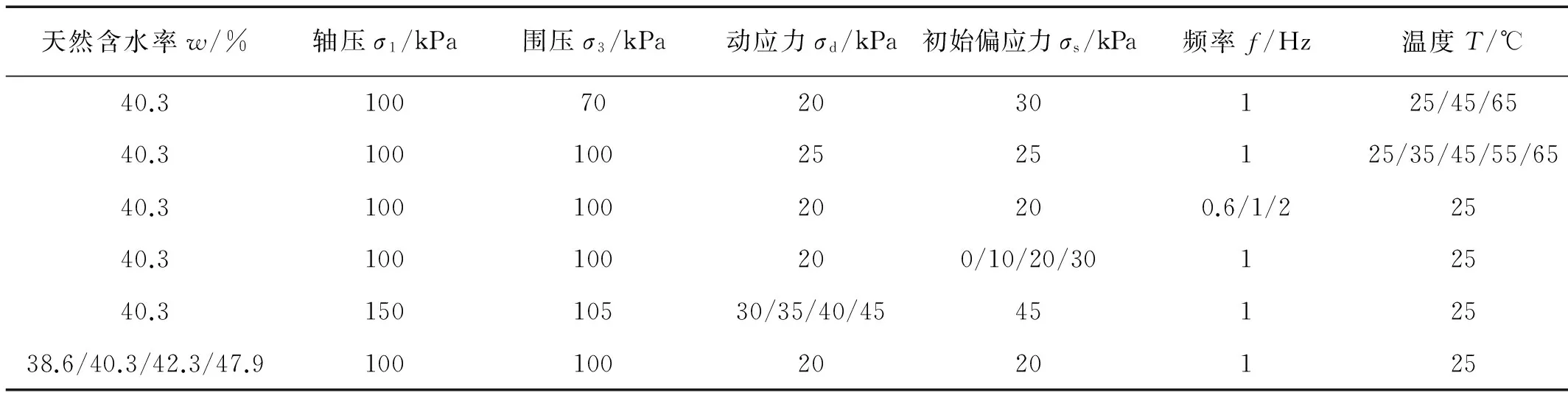
表2 試驗方案Tab. 2 Test plan

根據表2的試驗方案開展土的溫控動三軸試驗，計算得到不同溫度、頻率、初始偏應力、動應力和含水率下試樣的累積塑性應變與振動次數的關系曲線。由于文獻[16]對不同溫度下土的動孔壓、動彈性模量、動阻尼比特性開展了研究，在此不再贅述。本文重點考慮溫度、頻率、初始偏應力和含水率對塑性累積應變的影響，計算公式為

(1)

式中：εd為第N次循環中的累積塑性應變；εN,max，εN,min分別為第N次循環中最大與最小軸應變。

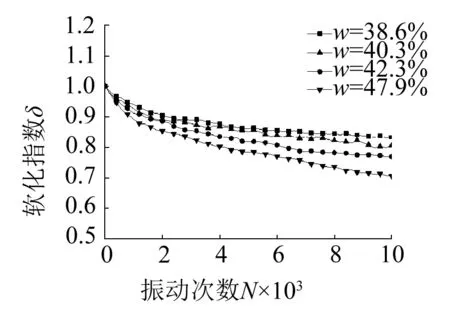
不同溫度、振動頻率、初始偏應力、動應力和含水率下的累積塑性應變與振動次數關系曲線如圖1所示。在不同的振動條件下，試樣的累積塑性應變均隨著振動次數的增加而增大。當關系曲線為穩定型時，累積塑性應變在振動初期變化較快，隨著振動試樣被逐漸壓密，應變增量逐漸減小，關系曲線基本趨于穩定，如圖1(a)、1(c)、1(d)、1(f)所示。當關系曲線為破壞型時，試樣的累積塑性應變在有效的振動次數內迅速增大直至破壞，如圖1(b)、1(e)所示。在振動次數相同的條件下，累積塑性應變隨著溫度的升高(25 ℃→65 ℃)，頻率的增大(0.6 Hz→2 Hz)，初始偏應力的減小(30 kPa→0 kPa)，動應力的減小(45 kPa→30 kPa)，含水率的減小(47.9%→38.6%)而減小，且減小的幅度也逐漸變小。

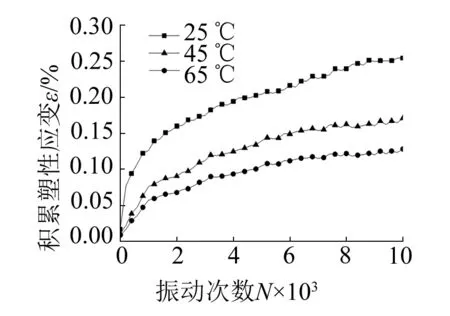
(a) σ1=100 kPa,σ3=70 kPa,σd=20 kPa,f=1 Hz

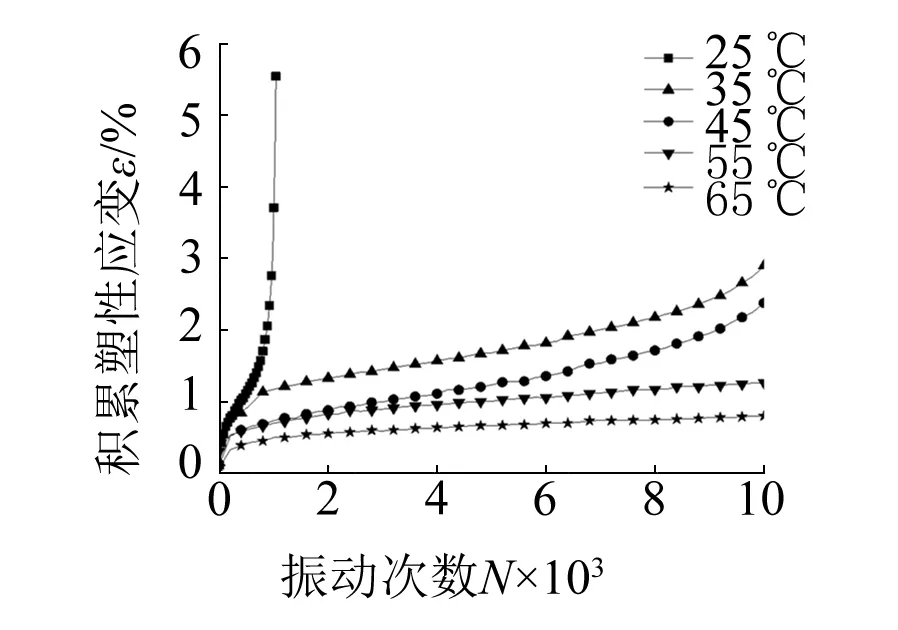
(b) σ1=σ3=100 kPa,σd=σs=25 kPa,f=1 Hz

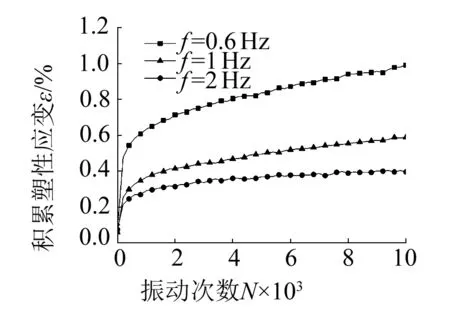
(c) σ1=σ3=100 kPa,σd=σs=20 kPa,T=25 ℃

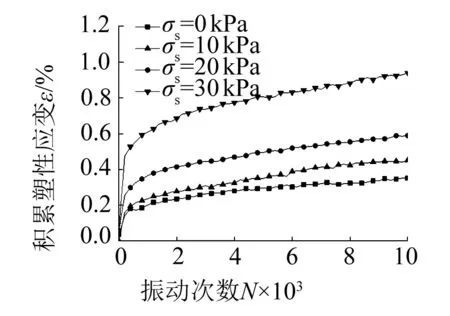
(d) σ1=σ3=100 kPa,σd=20 kPa,f=1 Hz,T=25 ℃

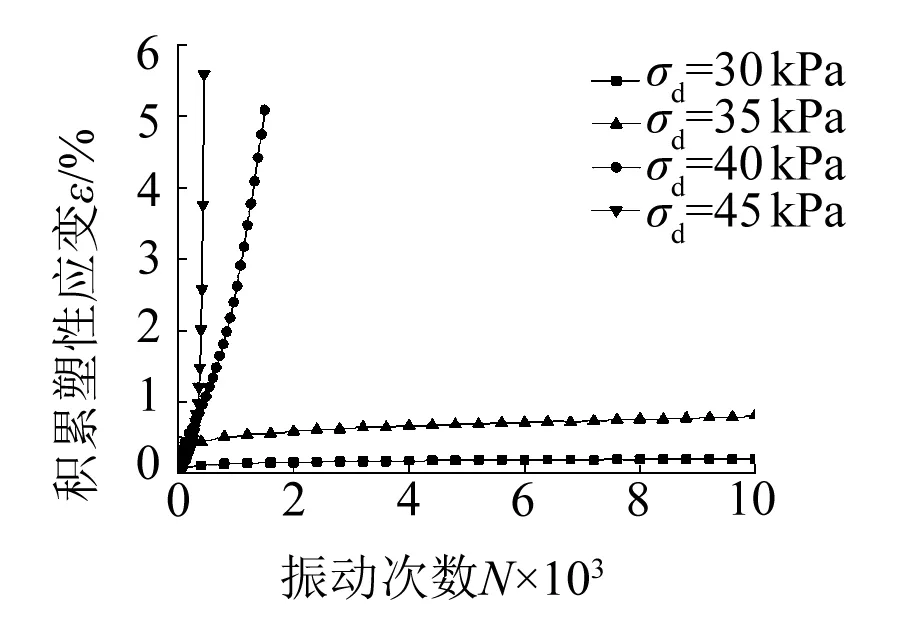
(e) σ1=150 kPa,σ3=105 kPa, σs=45 kPa,f=1 Hz,T=25 ℃

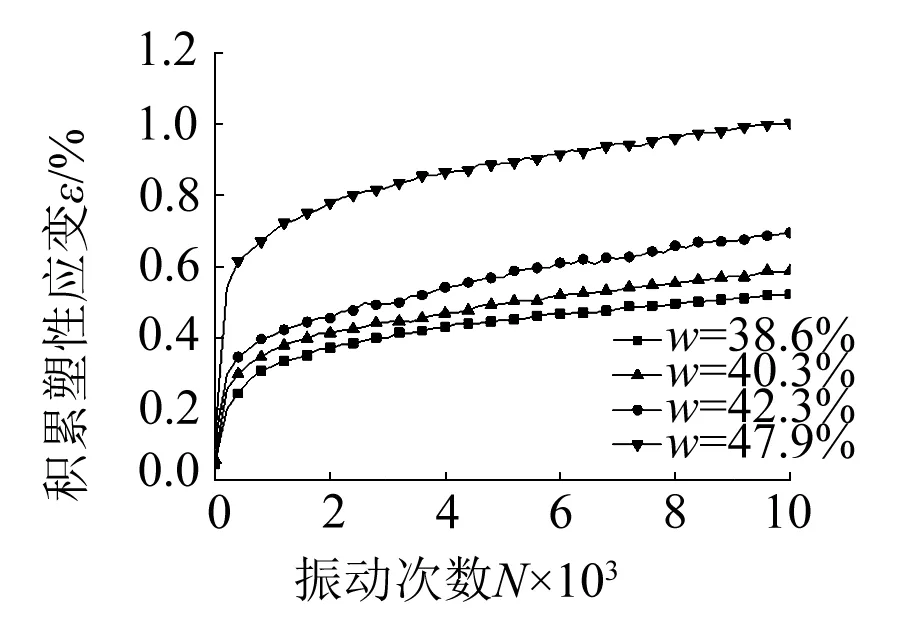
(f) σ1=σ3=100 kPa,σd=σs=20 kPa,f=1 Hz,T=25 ℃

1.2 土的應變軟化試驗結果

根據文獻[5]和[7]有關軟化指數的概念可知，軟化指數越大，土體軟化程度越小，土體振動過后存留的強度越大，具體表達式為

(2)

式中：δ為軟化指數；GSN，GS1分別為第N次和第1次循環中土體的割線剪切模量；ε1,max，ε1,min分別為第1次循環中最大與最小軸應變；εN,max，εN,min分別為第N次循環中最大與最小軸應變。

利用式(2)對2.1節各試驗工況下累積塑性應變數據，建立軟化指數δ與振動次數N關系如圖2所示，可以看出：在各試驗工況下，軟化指數隨振動次數的增加逐漸減小，土體的軟化程度提高。

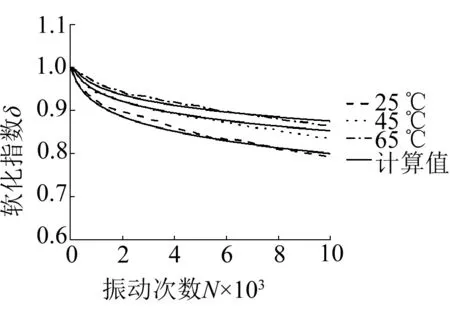
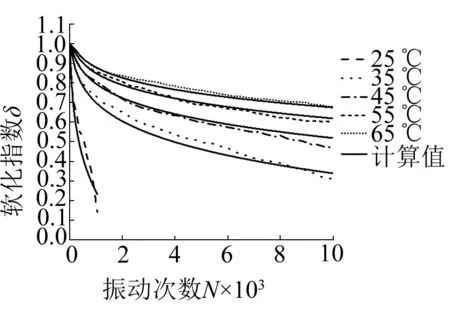
由圖2(a)、2(b)可知，在相同振動次數下，土的軟化指數隨著溫度的升高而增大，這主要是因為溫度的升高，土體表現出熱硬化特性，土體的動強度增大，土的軟化特性減弱。另外，對比圖2(a)的k0固結(σ1=100 kPa，σ3=70 kPa)和2(b)的各向等壓固結(σ1=σ3=100 kPa)的試驗結果可以看出：在N=100 00次、溫度為25 ℃和65 ℃時，k0固結條件下的分別為0.79和0.86，可見試驗溫度在25 ℃～65 ℃之間，軟化指數的增幅Δδ為0～0.07；而各向等壓固結25 ℃時土樣在N=1 000次左右即發生破壞，軟化指數急劇減小。土樣在N=10 000次，35 ℃時= 0.31，65 ℃時δ= 0.68，試驗溫度在35 ℃～65 ℃之間，軟化指數的增幅Δδ=0～0.37。由圖2(b)可以看出，隨著溫度的升高，軟化指數衰減有所減緩，曲線形式從破壞型向穩定型變化，在此過程土體強度有了較大幅度的提高，試樣從破壞型發展為穩定型。

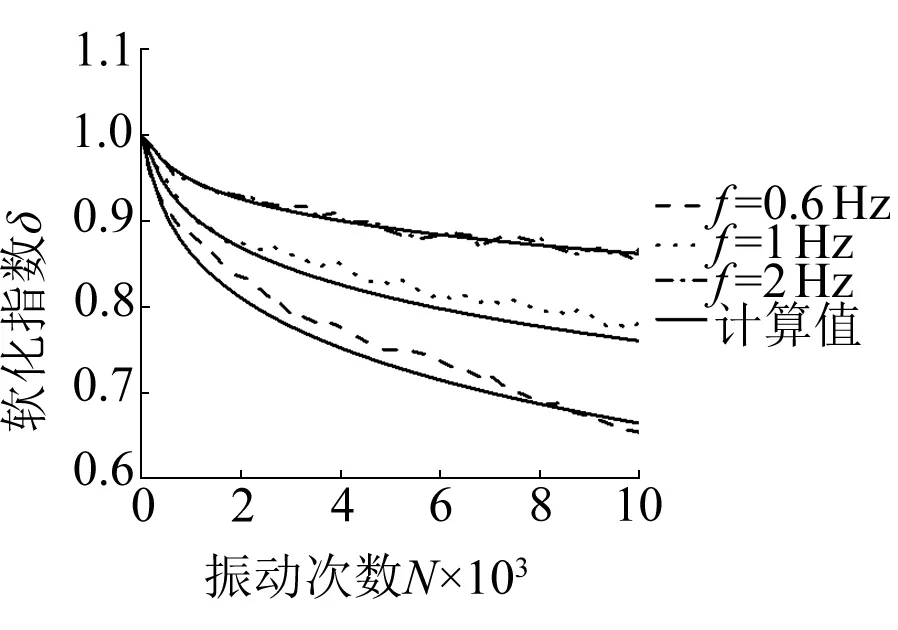
圖2(c)為25 ℃時不同振動頻率下軟化指數與振動次數的關系，可以看出：荷載振動頻率越小，土樣軟化指數越小，軟化程度越高；頻率越大，土樣軟化指數越大，軟化程度越低。這與文獻[7，9]的研究結果一致，其主要原因是土樣在低頻作用下，循環荷載變化慢，作用時間長，更有利于土體的壓密，孔壓有足夠的時間上升，從而導致土樣產生更大的變形[18-19]。

初始偏應力對軟化指數的影響如圖2(d)所示，軟化指數隨初始偏應力的增大而減小，且減小的幅度越來越大，例如當初始偏應力從0 kPa到10 kPa時，軟化指數差值約為0.03；從10 kPa到20 kPa時的軟化指數差約0.04；從20 kPa到30 kPa時的差值約0.16。

動應力對軟化指數的影響如圖2(e)所示，在不同動應力下，軟化指數衰減程度大不相同，關系曲線表現也不同。當動應力為30 kPa時，軟化指數衰減很小，振動10 000次后軟化指數約為0.87，并趨于穩定；當動應力為35 kPa時，軟化指數衰減變大，振動10 000次后軟化指數約為0.72，仍未趨于穩定，隨著振動的繼續，軟化指數將會繼續減小；當動應力為40 kPa時，軟化指數衰減迅速，振動1 500次后土樣破壞，軟化指數約為0.49；當動應力為45 kPa時，軟化指數近似線性衰減，振動450次后土樣破壞，軟化指數僅為0.12。循環荷載作用下，飽和軟黏土存在臨界循環動應力，該工況下土樣的臨界動應力為35～40 kPa之間。

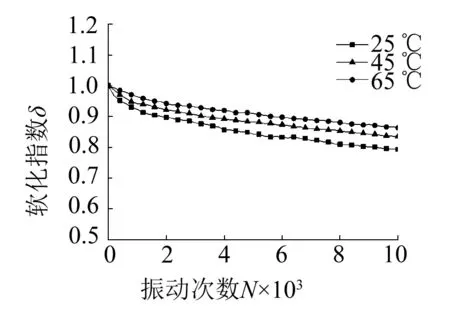
(a) σ1=100 kPa,σ3=70 kPa,σd=20 kPa,σs=30 kPa,f=1 Hz

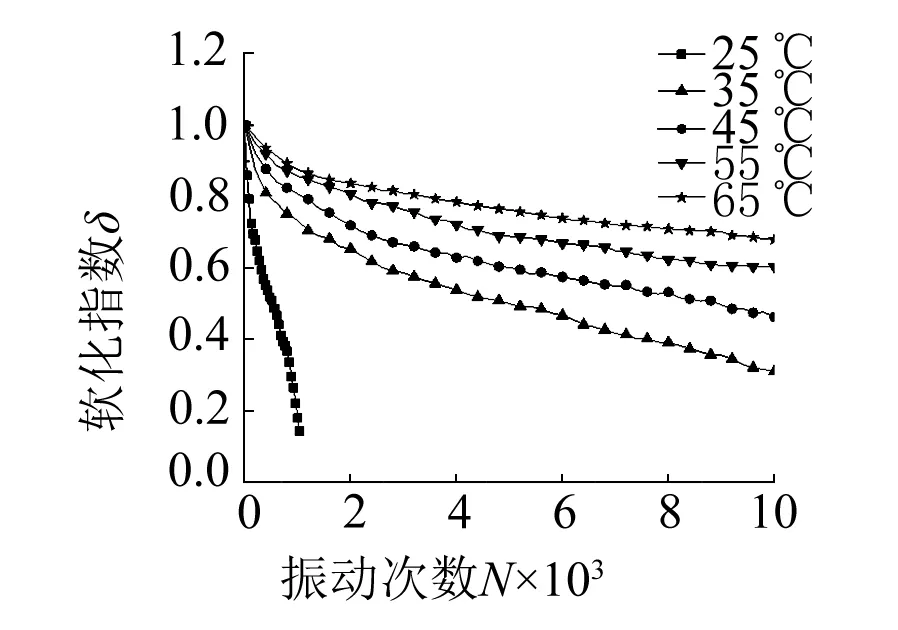
(b) σ1=σ3=100 kPa,σd=σs=25 kPa,f=1 Hz

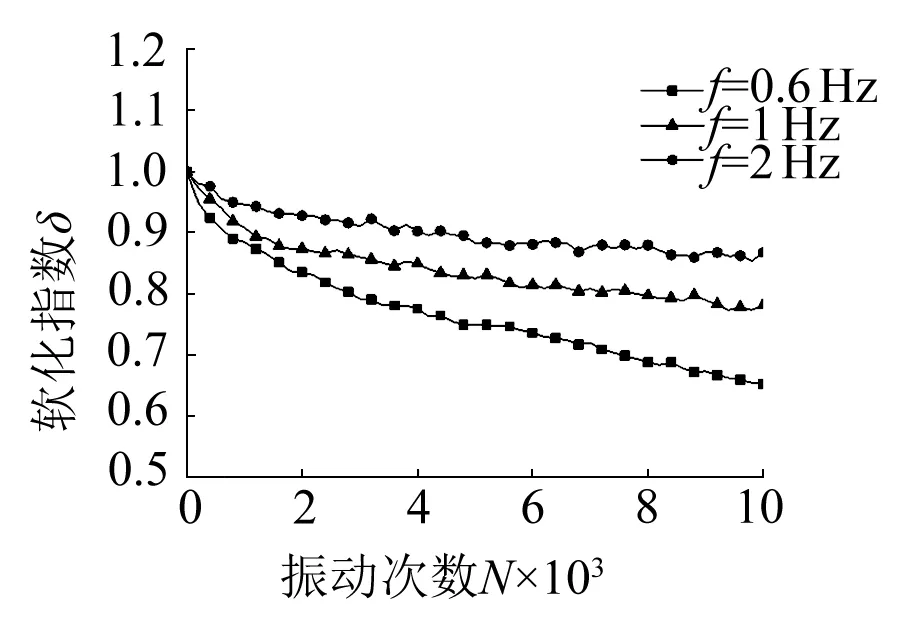
(c) σ1=σ3=100 kPa,σd=σs=20 kPa,T=25 ℃

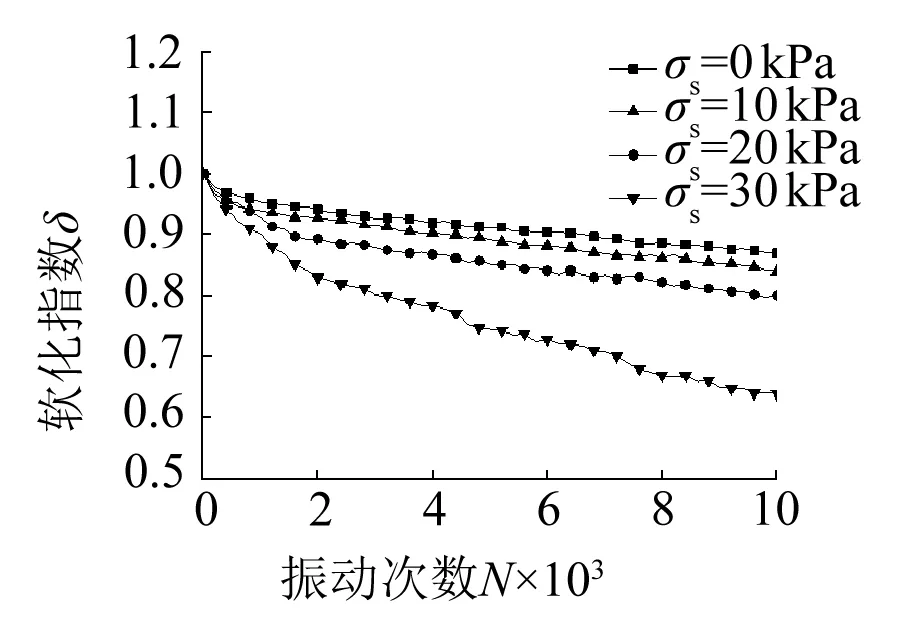
(d) σ1=σ3=100 kPa,σd=20 kPa,f=1 Hz,T=25 ℃

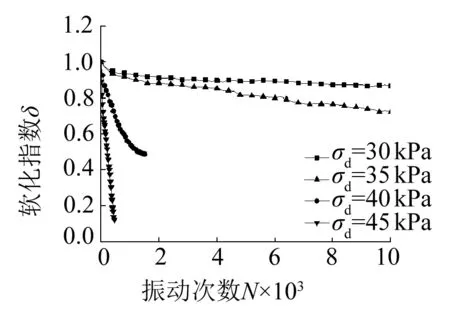
(e) σ1=150 kPa,σ3=105 kPa, σs=45 kPa,f=1 Hz,T=25 ℃

(f) σ1=σ3=100 kPa,σd=σs=20 kPa,f=1 Hz,T=25 ℃

土樣初始含水率變化對軟化指數的影響如圖2(f)所示。由圖中可知，軟化指數隨著含水率的增大而減小，振動10 000次后軟化指數從0.83減小到0.71。這是因為土體對水的作用非常敏感，初始含水率不同，土體發生物理和化學反應的程度也不同，土體內部結構性、連接強度也隨之不同，隨著含水率的增大，使得土體內的部分可溶鹽類膠結物溶解，而黏粒遇水后其膠結性會弱化，降低了其抵抗破壞變形的能力[20]，故試樣的軟化指數隨著含水率的增大而減小。

2 考慮溫度影響的應變軟化模型

在循環荷載作用下，從理論上推導建立土的應變軟化模型較為困難，而根據試驗結果進行回歸分析建立土的應變軟化經驗模型可以較好地描述土的應變軟化特性。IDRISS等提出了描述應變軟化的指數表達式為

δ=N-d

(3)

YASUHARA等提出了應變軟化半對數關系表達為

δ=1-DlgN

(4)

式中：d，D為軟化參數；N為振動次數。

以上兩種描述應變軟化的表達式較為簡單實用，但未能考慮循環荷載頻率、初始偏應力等試驗參數的影響，尤其是不能考慮應變的非線性以及溫度的影響，為此，本文在上述模型基礎上，分別建立考慮固結和各向等壓固結，溫度、頻率、初始偏應力、動應力和含水率因素影響的應變軟化模型為

δ=1-α1α2α3α4α5lgN-β1β2β3β4β5(lgN)2

(5)

δ=1-α1α2α3α4α5lgN-β0β2β3β4β5(lgN)2

(6)

式中：α1，β1為k0固結時反映溫度影響的參數；α0，β0為等壓固結時反映溫度影響的參數；α2，β2為反映頻率影響的參數；α3，β3為反映初始偏應力影響的參數；α4，β4為反映動應力影響的參數；α5，β5為反映含水率影響的參數。上述模型參數為非耦合關系，當不考慮某一影響因素時，可直接將模型中相應參數取1。例如溫度參數α0，β0，α1，β1等于1時，即可退化為王軍、蔡袁強等的模型。

不考慮各參數之間的耦合作用，各參數的表達式為

α2=A2f2+B2f+C2

β2=a2lnf+b2

α5=A5w2+B5w+C5

β5=a5w2+b5w+c5

利用軟化模型表達式(5)、(6)對土的應變軟化試驗結果進行擬合，得到各參數結果為

A1=-0.000 313,B1=0.001 875,C1=-0.039 563,

a1=0.001 56,b1=-0.008 75,c1=0.029 2,A0=0.006 5,B0=-0.046 8,C0=0.116 5,D0=-0.184 3,

a0=0.082,b0=-3.206,c0=0.038,

A2=-0.005 9,B2=0.039 4,C2=-0.089 5,

a2=-0.017,b2=0.029,

A3=-0.019,B3=-0.78,C3=2.11,

a3=0.012,b3=0.457,c3=2.3,A4=-105.351,B4=89.679,C4=-25.567,D4=2.363,

a4=65.36,b4=-36.53,c=7.253,d4=-0.502

A5=4.24,B5=-4.009 1,C5=0.877 2

a5=-1.662 5,b5=1.604 7,c5=-0.351 6,

在獲得試驗相關參數后，再利用應變軟化模型的表達式(5)、(6)對相關試驗工況進行計算，并與試驗結果進行對比，結果如圖3所示。

(a) σ1=100 kPa,σ3=70 kPa,σd=20 kPa,σs=30 kPa,f=1 Hz

(b) σ1=σ3=100 kPa,σd=σs=25 kPa,f=1 Hz

(c) σ1=σ3=100 kPa,σd=σs=20 kPa,T=25 ℃

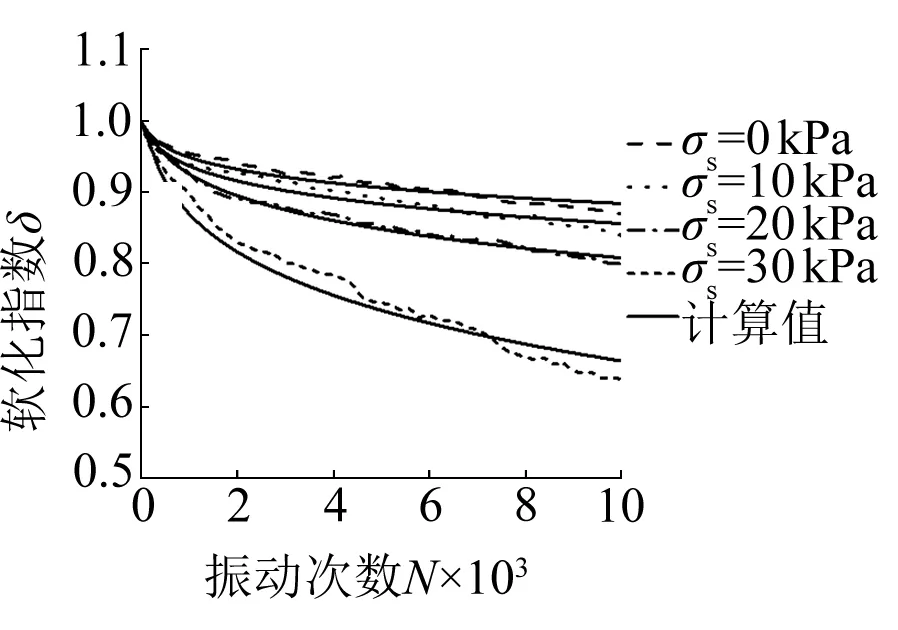
(d) σ1=σ3=100 kPa,σd=20 kPa,f=1 Hz,T=25 ℃

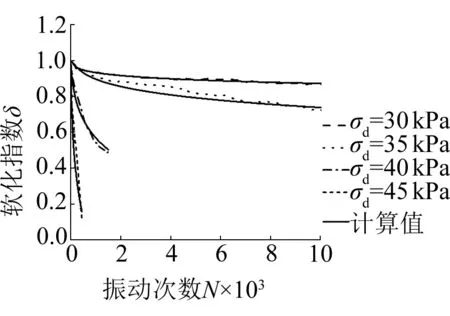
(e) σ1=150 kPa,σ3=105 kPa, σs=45 kPa,f=1 Hz,T=25 ℃

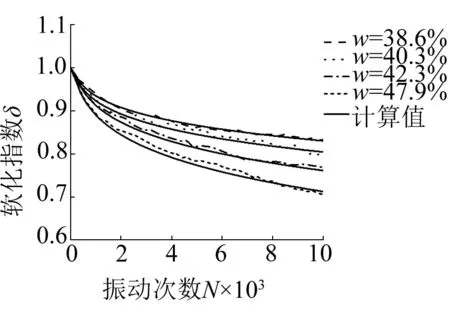
(f) σ1=σ3=100 kPa,σd=σs=20 kPa,f=1 Hz,T=25 ℃

由圖3可知，建立的經驗模型能夠較好的反映土體在不同溫度、頻率、初始偏應力、動應力、含水率和振動次數下的應變軟化情況。由式(5)、(6)的應變軟化模型可以計算獲得其他溫度、頻率、初始偏應力、動應力和含水率下的軟化指數。

3 結 論

在對寧波飽和軟黏土開展了溫控動三軸試驗后，建立了考慮了溫度、頻率、初始偏應力、動應力和含水率影響的應變軟化模型，主要結論如下：

(1) 在不同的溫度、頻率、初始偏應力、動應力和含水率下，試樣的累積塑性應變均隨著振動次數的增加而增大。當振動次數相同時，累積塑性應變隨溫度的升高，頻率的增大而減小；隨初始偏應力、含水率的增大而增大。

(2) 在各試驗工況下，土的軟化指數隨振動次數的增大而減小，且與振動次數關系表現為非線性。

(3) 隨著溫度的升高，軟化指數逐漸增大，土體強度增大，曲線從破壞型轉為穩定型。軟化指數隨著頻率增大而增大，隨初始偏應力、動應力和含水率的增大而減小。

(4) 利用試驗數據建立的應變軟化模型能反映溫度、頻率、初始偏應力、動應力、含水率等因素的影響，并能預測同一試驗工況下不同參數取值的結果。

[ 1 ] YASUHARA K, YAMANOUCHI T，HIRAO K. Cyclic strength and deformation of normally consolidation clay[J]. Soils and Foundations, 1982, 22(3):77-79.

[ 2 ] LEFEBVRE G, PFENDLER P. Strain rate and preshear effects in cyclic resistance of soft clay[J]. Journal of Geotechnical Engineering, 1987, 113(5): 476-489.

[ 3 ] HICHER P Y , LADE P V. Rotation of principal directions inK0consolidated clay[J]. Journal of Geotechnical Engineering, 1987, 113(7): 774-788.

[ 4 ] MATASOVIC N, VUCETIC M. Generalized cyclic-degradation-pore-pressure generation model for clays[J]. Journal of Geotechnical Engineering, 1995, 121(1): 33-42.

[ 5 ] IDRISS I M, DOBRY R, SINGH R D. Nonlinear behavior of soft clays during cyclic loading[J].Journal of Soil Mechanics and Foundation,1978, 104(12): 1427-1447.

[ 6 ] YASUHARA K, HYDE A F L,TOYOTA N, et al. Cyclic stiffness of plastic silt with an initial drained shear stress[C]// Proc Geotechnique Symp on Pre-failure Deformation of Geomterials. London:Thomas Telford Ltd.,1998:373-382.

[ 7 ] 周建,龔曉南.循環荷載作用下飽和軟黏土應變軟化研究[J]. 土木工程學報, 2000,32(5):62-68. ZHOU Jian, GONG Xiaonan. Study on strain softening in saturated soft clay under cyclic loading[J].China Civil Engineering Journal, 2000, 32(5): 62-68.

[ 8 ] 王軍,蔡袁強,徐長節,等.循環荷載作用下飽和軟黏土應變軟化模型研究[J]. 巖石力學與工程學報, 2007, 26(8): 1713- 1719. WANG Jun, CAI Yuanqiang, XU Changjie, et al. Study on strain degradation model in saturated soft clay under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8):1713-1719.

[ 9 ] 蔡袁強,陳靜,王軍.循環荷載下各向異性軟黏土應變-軟化模型[J]. 浙江大學學報(工學版),2008(6):1058-1064. CAI Yuan qiang, CHEN Jing, WANG Jun. Strain-degradation model for anisotropic soft clay under cyclic loading[J]. Journal of Zhejiang University(Engineering Science),2008(6):1058-1064.

[10] 地鐵設計規范:GB50157—2003 [S].

[11] AMPFO F, MAIDMENT G, MISSENDEN J. Underground rail way environment in the UK Part2: investigation of heat load[J]. Applied Thermal Engineering, 2004, 24:633-645.

[12] 羅飛,趙淑萍,馬巍,等. 分級循環荷載作用下凍土動應變幅值的試驗研究[J]. 巖土力學, 2014,35(1):123-129. LUO Fei, ZHAO Shuping, MA Wei, et al. Experimental study of dynamic strain amplitude of frozen soil under stepped axial cyclic loading[J]. Rock and Soil Mechanics, 2014, 35(1): 123-129.

[13] 楊果林,林宇亮,李昀. 新型加筋土擋墻動變形特性試驗研究[J]. 振動與沖擊, 2010,29(1):223-248. YANG Guolin, LIN Yuliang, LI Yun. Test study on dynamic deformation behavior of new reinforced earth retaining walls [J]. Journal of Vibration and Shock, 2010,29(1):223-248.

[14] 冷伍明,劉文劼,周文權. 振動荷載作用下重載鐵路路基粗顆粒土填料臨界動應力試驗研究[J]. 振動與沖擊, 2015,34(16):25-30. LENG Wuming, LIU Wenjie, ZHOU Wenquan. Testing research on critical cyclical stress of coarse-grained soil filling in heavy haul railway subgrade[J]. Journal of Vibration and Shock,2015,34(16):25-30.

[15] 朱遠武,鄭榮躍,劉干斌,等. 爆炸作用下淤泥質軟土的熱力響應試驗研究[J]. 振動與沖擊, 2014,33(24):64-70. ZHU Yuanwu, ZHENG Rongyue, LIU Ganbin, et al. Tests for temperature and pressure response of silt soft soil under blasting load [J]. Journal of Vibration and Shock, 2014, 33(24): 64-70.

[16] 劉干斌,范思婷,葉俊能,等. 溫控動三軸試驗裝置的研制及應用[J]. 巖石力學與工程學報, 2015, 34(7):1345-1352. LIU Ganbin, FAN Siting, YE Junneng, et al. Application and development of a temperature-controlled dynamic triaxial test system[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(7):1345-1352.

[17] ANDERSEN K H, LAURITZSEN R. Bearing capacity for foundations with cyclic loads[J]. Journal of Geotechnical Engineering, 1988, 114(5): 540-555.

[18] 唐益群,李珺,劉莎,等. 地鐵行車荷載作用下淤泥質黏土累積特性的試驗研究[J].工程地質學報, 2011(4):460-466. TANG Yiqun, LI Jun, LIU Sha, et al. Experimental study on the behavior of muddy clay under subway loading[J]. Journal of Engineering Geology, 2011(4): 460-466.

[19] 張茹,涂揚舉,費文平,等. 振動頻率對飽和黏性土動力特性的影響[J]. 巖土力學, 2006, 27(5): 699-704. ZHANG Ru, TU Yangju, FEI Wenping, et al. Effect of vibration frequency on dynamic properties of saturated cohesive soil[J]. Rock and Soil Mechanics, 2006, 27(5): 699- 704.

[20] 王峻,石玉成,王謙,等. 天然含水率狀態下原狀黃土動強度特性研究[J]. 世界地震工程, 2012(4):23-27. WANG Jun, SHI Yucheng, WANG Qian, et al. Study on dynamic strength properties of undisturbed loess under natural moisture content [J]. World Earthquake Engineering, 2012(4):23-27.

Strain softening of saturated soft clay considering the temperature effect

FAN Siting1, LIU Ganbin1, CHEN Bin2, YE Junneng2

( 1. Institution of Geotechnical Engineering, Ningbo University, Ningbo 315211, China; 2. Ningbo Urban Rail Transit Project Construction Headquarters, Ningbo 315010, China)

The phenomenon of strain softening usually occurs in saturated soft clay under cyclic loading. A temperature-controlled cyclic triaxial test on Ningbo saturated soft clay was carried out uner different temperature loadings, frequencies, initial deviator stresses, dynamic stresses and moisture contents, and a mathematical model which can reflect the strain softening reasonably was set up on the basis of the test. It is observed that the softening index reduces with the increase of vibration number, initial deviator stress, dynamic stress and moisture content. On the other hand, higher frequency and temperature will increase the softening index. The presented model can reasonably describe the effects of temperature, frequency, initial deviator stress, dynamic stress and moisture content on the soil strain softening.

temperature-controlled cyclic triaxial test; temperature effect; strain softening; softening index

國家自然科學基金資助項目(51278256；51478228)；浙江省新苗人才計劃(2014R405075)

2015-10-12 修改稿收到日期： 2016-01-25

范思婷 女，碩士生，1989年生

劉干斌 男，博士，教授，1976年生

E-mail:liugb76@163.com

TU43

A

10.13465/j.cnki.jvs.2017.06.001