低軌道下運行的衛星-太陽帆板系統的剛-柔-熱耦合動力學建模

左亞帥， 劉錦陽

(上海交通大學 船舶海洋與建筑工程學院，上海　200240)

低軌道下運行的衛星-太陽帆板系統的剛-柔-熱耦合動力學建模

左亞帥， 劉錦陽

(上海交通大學 船舶海洋與建筑工程學院，上海200240)

傳統地考慮熱效應的衛星-太陽帆板動力學模型只考慮太陽直接輻射熱流的影響，僅適用于高軌道運行的航天器。以低軌道下運行的衛星-太陽帆板系統為研究對象，提出了一種通用的分析其在宇宙空間各種熱流作用下剛-柔-熱耦合動力學特性的建模方法。考慮太陽帆板熱變形、衛星的姿態運動和太陽帆板受到的各種輻射的熱流密度之間的耦合關系，分別給出了太陽直接輻射熱流、地球紅外輻射熱流以及地球反照輻射熱流的計算公式。將系統視為中心剛體-懸臂梁模型，首先建立了懸臂梁的熱傳導方程，然后通過引入考慮熱應變的應力-應變關系，用虛功原理建立了衛星-太陽帆板多體系統的考慮熱效應的動力學方程，對熱傳導方程和動力學方程聯立求解。對低軌道下運行的衛星-太陽帆板系統進行了數值仿真分析，分析了考慮地球紅外輻射和地球反照輻射熱流對熱振動的影響，以及考慮剛-柔-熱耦合效應對系統動力學特性的影響，并給出了系統熱振動穩定時特征參數的范圍。

低軌道衛星-太陽帆板；剛-柔-熱耦合動力學；熱振動

航天器在軌運行時，不斷地受到宇宙空間各種熱流(主要是太陽直接輻射、地球反照輻射以及地球紅外輻射)的作用，由于太陽帆板上下表面接收到的熱流密度不同，太陽帆板表面及內部產生不均勻的溫度分布，隨著航天器的位置變化，這些熱流的大小也發生周期性的變化，導致太陽帆板表面及內部溫度場也不斷發生改變，從而使太陽帆板內部產生隨時間變化的熱應力。在內部熱應力的作用下，太陽帆板產生持續的熱變形及熱振動，同時引起航天器的姿態變化，有可能導致航天器失穩，無法完成既定的任務，甚至產生結構破壞，造成嚴重危險。

秦文波等[1]采用有限差分法對某剛性衛星太陽帆板進行熱分析，通過數值求解得到了剛性太陽帆板表面的溫度場分布，及其隨時間的變化情況；LI等[2]在對復合材料太陽帆板陣進行研究時，考慮了軌道高度、地球陰影區等因素的影響，采用有限元法，得到了衛星在不同軌道高度下運行過程中，太陽帆板的全域溫度場及其時變情況。雖然他們的研究都考慮了太陽直接輻射熱流、地球紅外輻射熱流以及地球反照輻射熱流的綜合作用，但是由于研究對象是剛性太陽帆板，因而他們都沒有考慮到太陽帆板的熱變形和熱流密度之間的耦合效應。喬博[3]利用軟件Marc2003分析了某柔性復合材料太陽帆板在各種空間熱流作用以及其他因素的影響下的溫度場分布規律，為結構分析提供了參考依據。孔祥宏等[4-6]在研究航天器柔性附件時，采用熱-結構解耦方式求解，得到了航天器運行全周期內結構的溫度場分布以及變化情況，將溫度場變化情況輸入到結構計算有限元程序中，得到了結構的動態響應，并進行了仿真分析。JOHNSTON等[7-8]采用混合坐標法，推導了太陽帆板的熱振動方程，通過數值計算得到了太陽帆板自由端的端點的熱變形，進而又研究了太陽帆板的熱擾動對衛星運動的影響；薛明德等[9-12]在研究簡單的hub-beam耦合系統時，建立了中心艙體-外部活動部件的中心剛體-懸臂梁模型，采用有限元分析方法，建立了由柔性附件的熱-結構耦合的瞬態熱傳導方程以及航天器中心剛體-懸臂梁的剛-柔耦合動力學方程組成的剛-柔-熱耦合的系統方程，通過數值分析，揭示了系統的熱振動現象，雖然他們在研究過程中考慮了衛星-太陽帆板的剛-柔-熱耦合效應，但是熱分析都只考慮了太陽直接輻射熱流，沒有考慮地球紅外輻射熱流以及地球反照熱流的影響。

本文以低軌道下運行的衛星-太陽帆板系統為研究對象，假定衛星太陽帆板始終對日定向，綜合考慮太陽直接輻射熱流、地球紅外輻射熱流以及地球反照輻射熱流的影響，考慮系統的熱變形和熱振動與熱流之間的耦合效應，采用中心剛體-懸臂梁模型，通過將系統的熱傳導方程與動力學方程聯立，建立系統的剛-柔-熱耦合模型，進而揭示了系統的熱振動現象；通過數值計算，給出了耦合效應以及除太陽直接輻射熱流以外的地球紅外輻射熱流和地球反照輻射熱流的影響，熱振動穩定時，衛星中心剛體與太陽帆板轉動慣量之比、太陽帆板初始姿態角以及太陽帆板阻尼系數之間的關系。

1　宇宙空間熱流計算

圖1為地球陰影區劃分示意圖，P表示衛星所處位置，PA相切太陽于A點，PB相切地球于B點γ1、γ2、γ3意義如圖所示。圖2標注了衛星運行到某一位置時與熱流計算相關的角度，αθ表示太陽帆板表面法線與陽光負方向的夾角，β表示太陽帆板表面法線與星地連心線的夾角。根據衛星所處區域的不同，太陽帆板表面單元dA接受到的太陽直接輻射熱流角系數ψ1，地球紅外輻射熱流角系數ψ2以及地球反照輻射熱流角系數ψ3[13]可表示如下

(1)

(2)

(3)

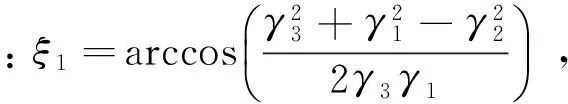
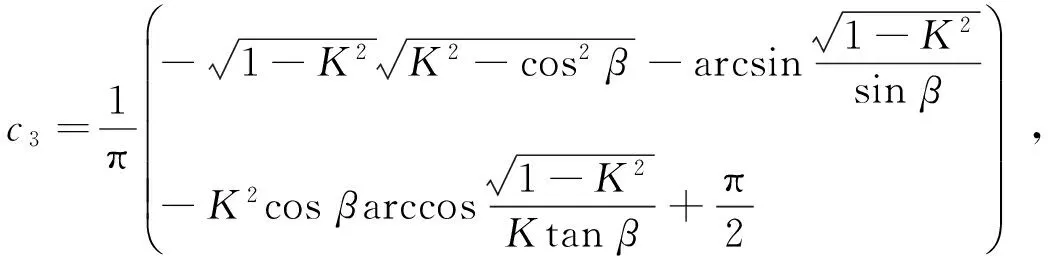
如圖3所示，建立衛星-太陽帆板的中心剛體-懸臂梁模型。取衛星太陽帆板對日定向、初始姿態角為零時中心剛體的連體基o-xy為參考基，衛星中心剛體為剛體Ⅰ，建立連體基O1-x1y1，兩塊太陽帆板取為剛體Ⅱ和Ⅲ，并建立浮動基O2-x2y2和O3-x3y3。φ為衛星與地心連心線和日地連心線的夾角(表征衛星所處軌道位置)，θ2為太陽帆板Ⅱ的浮動基相對參考基的轉角，θ3為太陽帆板Ⅲ的浮動基-x相對參考基的轉角。

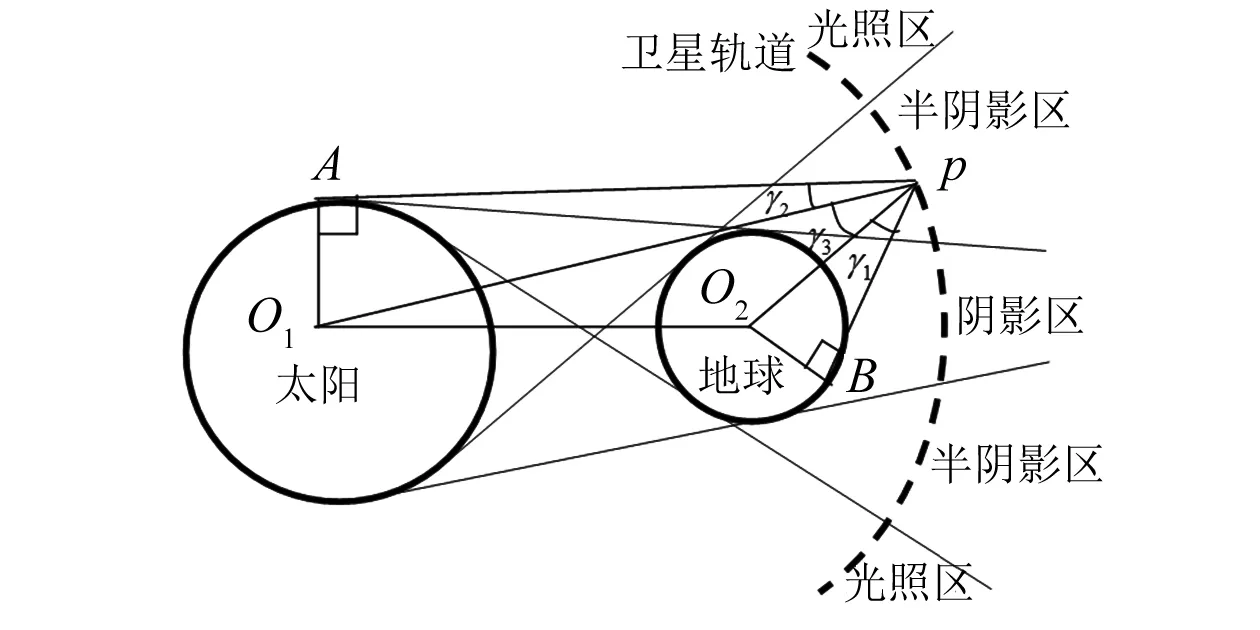
圖1　軌道陰影區示意圖Fig.1 Shadows of the earth

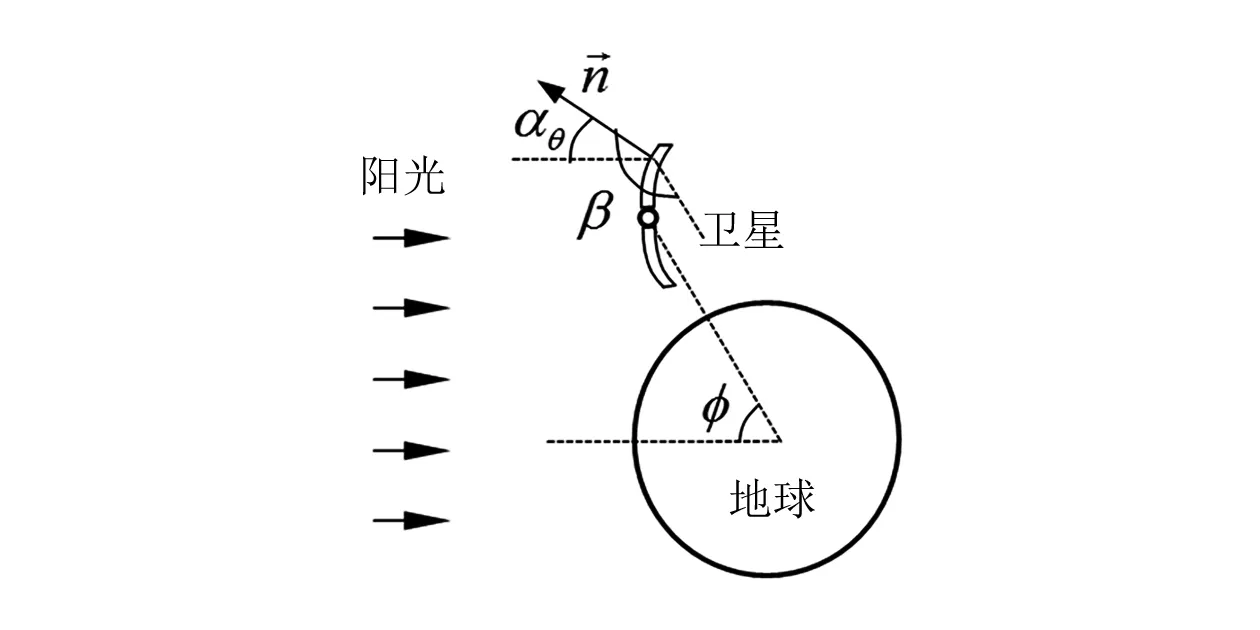
圖2　衛星運行過程示意圖Fig.2 Illumination of the satellite in orbit

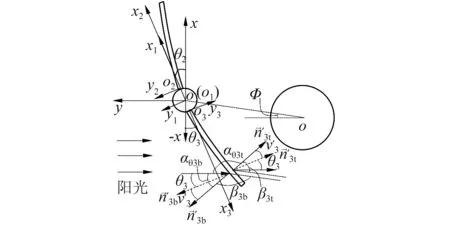
圖3　衛星-太陽帆板剛-柔-熱耦合模型Fig.3 Rigid-flexible-thermal coupling modelof satellite-solar panel system

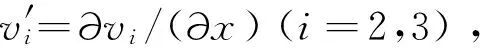
(4a)

太陽帆板Ⅲ下表面(y3=-h/2)熱流計算相關角度為

(4b)

同理可得太陽帆板Ⅱ上下表面熱流計算相關角度。為方便起見，本文后續仿真分析均以太陽帆板Ⅲ為準。

太陽帆板表面接受到的凈熱流為吸收到的宇宙空間熱流與自身向外輻射的熱流之差，即：

(5)

式中，αi為該表面的吸收率，S0為太陽輻射常數，ρE為地球表面平均反照率，εE為地球表面發射率，TE為地球表面平均溫度，σ為史蒂芬玻爾茲曼常數，εi為該表面的發射率，Ti為該單元表面的溫度。

2　有限元離散熱傳導方程的建立

熱傳導方程及其邊界條件的等效積分形式為

(6)

式中：ρ為材料密度；c為材料的比熱容；kx，ky為材料x，y方向的熱傳導系數；Qt為材料內熱源強度；nx,ny為邊界外法線在x,y方向上的投影，h為材料的對流換熱系數，Ta為環境溫度；Γ2對應第二類邊界條件的表面；Γ3對應第三類邊界條件的表面。

對于本文研究采用的柔性梁模型，將梁上任一點的溫度沿y方向進行泰勒展開：

(7)

式中，Tr為參考溫度，T0(x,t)表示梁中線上的點的溫度分布，T(k)(x,t)表示中線上的點的溫度在y方向上的k階導數。

采用一致質量法對柔性梁進行有限元離散，將柔性梁等分為N個單元，則梁上任一點的第k階溫度導數可表示為

(8)

式中，Sek為單元形函數矩陣，Bek為布爾矩陣。

將式(7)，(8)代入式(6)，熱傳導方程的等效積分形式化為如下形式：

(9)

式中，Cij，Kij，Fi的具體表達式見文獻[14]。

因此，可得柔性平面梁的有限元離散熱傳導方程為

(10)

衛星在太空中運行時,處在高真空的環境下，熱輻射為太陽帆板接收到的主要外熱流，熱對流可以忽略不計，即h+=h-=0，太陽帆板本身無內熱源，故Qt=0，而q+,q-可以由式(5)得到。

3　衛星-太陽帆板系統動力學方程

本文采用的平面柔性梁模型基于以下假設：①歐拉-伯努利梁，材料各向同性均勻，截面處無偏心距，變形后的截面仍垂直于梁的中面，梁為小變形；②太陽帆板彈性模量在研究過程中不隨溫度變化而變化(太陽帆板溫度變化不大，影響可以忽略)。

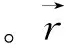
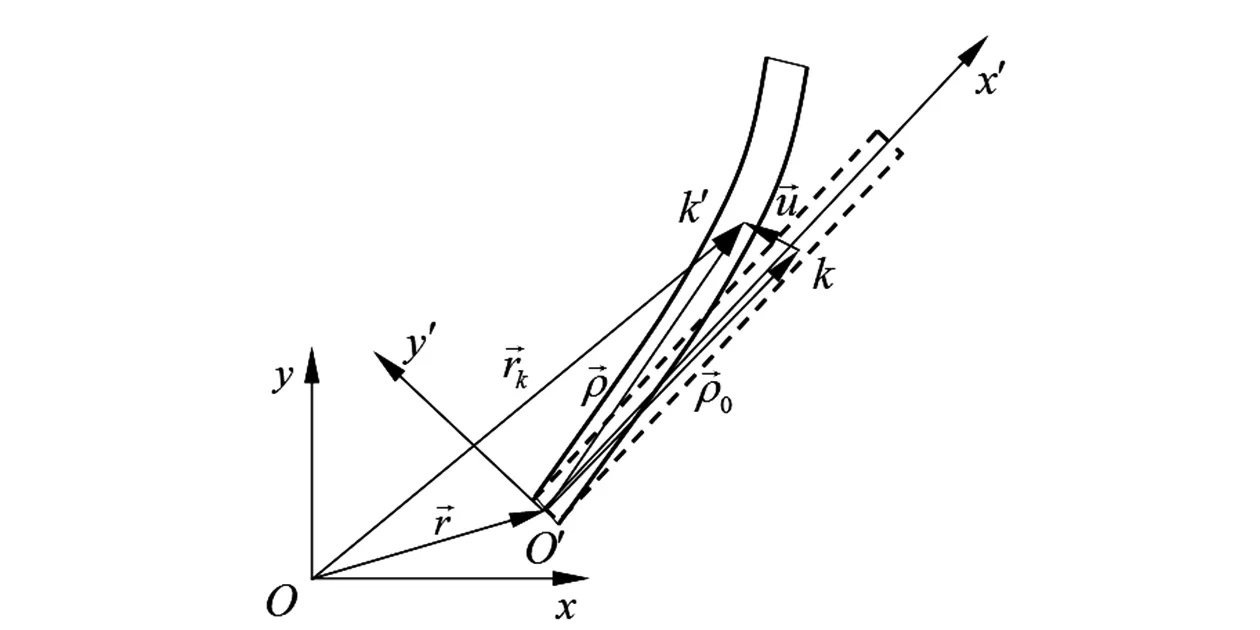
圖4　作大范圍平面運動的柔性梁模型Fig.4 Model of the flexible beam in large overall motion

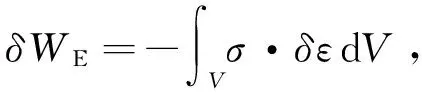
(11)

式中：A為柔性梁的橫截面積；L為柔性梁的長度；I為柔性梁對中面的慣性矩。

對于離散化的柔性梁，中線上任意一點的伸長量及橫向變形位移可用下式表示：

(12)

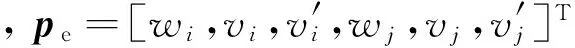
δWE=δpT(-KEp+FT)

(13)

其中，

(14)

(15)

由Jourdain速度變分原理，可得單平面梁Bi的動力學變分方程：

(16)

式中，Mi為廣義質量陣，Qi為廣義力陣，可表示為Qi=Qii+QiF+[0T(-KiEqi+FiT)T]T,其中，Qii表示離心力和哥氏慣性力項之和，QiF表示外力引起的廣義力陣。Mi，Qii和QiF表達式見參考文獻[9]。

對于本文選取的衛星-太陽帆板所系統，如圖3所示，選取系統廣義坐標陣為：

式中φi表示剛體姿態角。

引入拉格朗日乘子λ，利用第一類拉格朗日方程增廣形式，將系統約束方程引入，得到考慮剛-柔-熱耦合效應的系統的動力學方程：

(17)

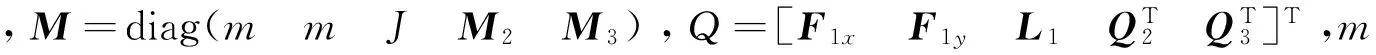
4　數值仿真及分析

本文所采用的衛星及太陽帆板的參數如下：太陽帆板長度L=7.5 m，假定橫截面為均勻的矩形，橫截面的寬B=0.02 m，高度H=0.02 m，密度ρ=36.8 kg/m3，彈性模量E=1.93×109Pa，熱膨脹系數αT=2.3×10-5K-1，斯特潘玻爾茲曼常數σ=5.670×10-8W/(m2·K4)，比熱容c=921 J/(kg·K)，熱傳導系數kx=ky=15 W/(m·K)，衛星中心剛體回轉半徑取為RC=1 m，太陽帆板表面的吸收率α=0.79，太陽帆板面向太陽的一面的發射率ε1=0.81，太陽帆板背向太陽的一面的發射率ε2=0.86，地球半徑RE=6.4×106km，地球表面發射率εE=0.7，地球表面反射率ρE=0.3，地球表面溫度TE=289 K，日地距離RSE=1.496×1011m，太陽半徑RS=6.963×103m，太陽輻射常數S0=1 350 W/m2。計算所取的溫度場的泰勒展開式的階數m=3，太陽帆板限元離散單元數取為N=10。

4.1綜合熱流仿真分析

如圖5 所示，橫坐標表示衛星所處軌道位置，縱坐標表示太陽帆板表面接受到的熱流密度，圖(a)表示只有太陽輻射熱流時的作用結果，圖(b)表示太陽直接輻射熱流、地球反照輻射熱流以及地球紅外輻射熱流的綜合作用結果。與只考慮太陽直接輻射的熱流情況對比可以發現，在低軌道情況下，地球紅外輻射熱流以及地球反照輻射熱流對衛星太陽帆板對日面影響較小，但是對太陽帆板背日面影響較大，尤其是在會日點附近，影響尤為顯著(會日點附近地球反照熱流影響明顯)。因而，研究過程中，需要考慮地球紅外輻射熱流以及地球反照輻射熱流的綜合影響。

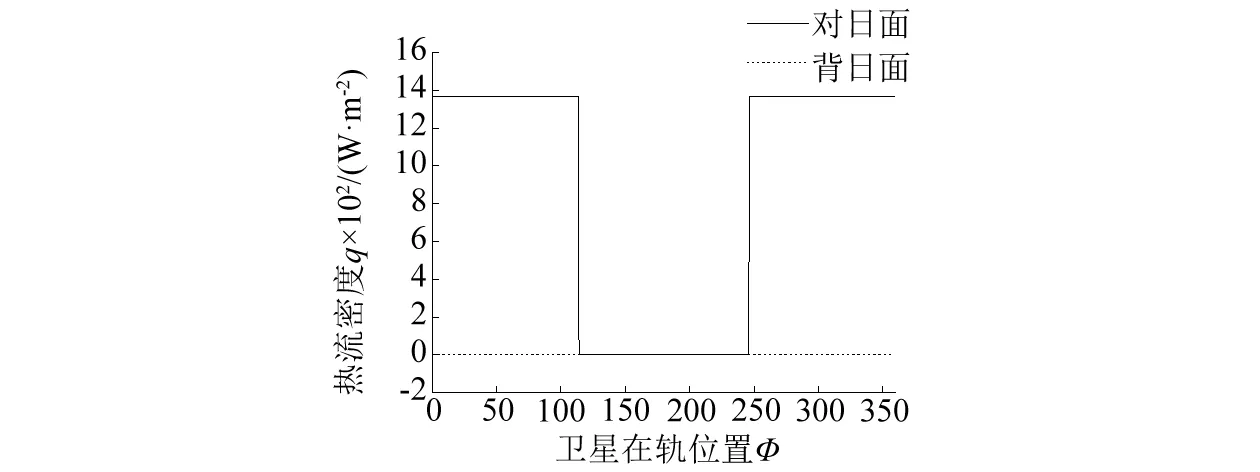
(a)綜合熱流

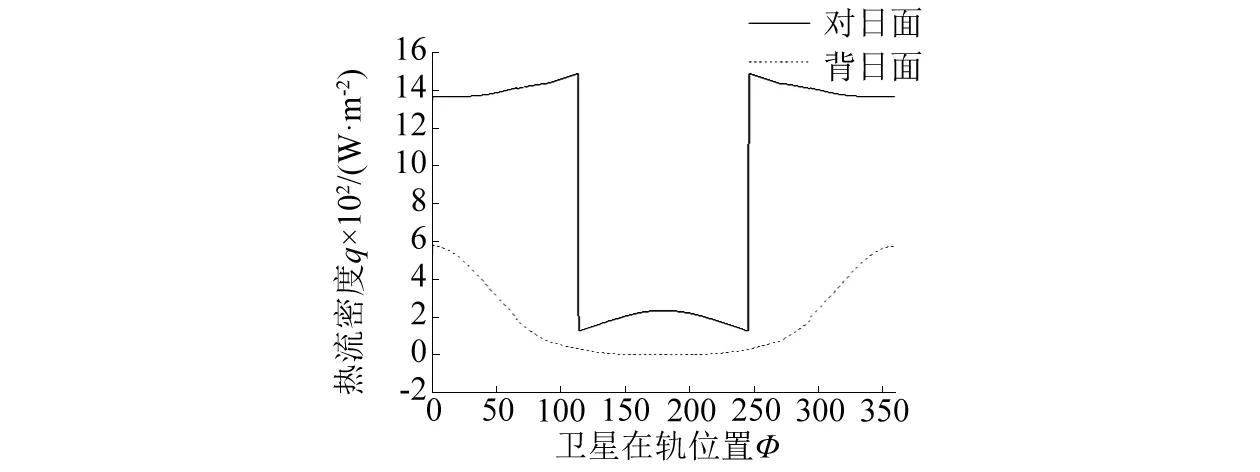
(b)太陽直接輻射熱流

4.2耦合效應對于太陽帆板熱變形的影響

如圖6所示，衛星處于φ=0°，初始姿態角φ=20°，太陽帆板阻尼系數ζ=0.4×10-3，轉動慣量之比η=200(無量綱量η=Jc/J表示衛星中心剛體與太陽帆板的轉動慣量之比)時，耦合和非耦合(熱流密度不隨太陽帆板熱變形和衛星的姿態的變化而變化)時衛星熱運動情況對比。由圖可知，不考慮耦合效應時，太陽帆板上下表面溫度差、太陽帆板端點撓度、中心剛體相對初始姿態角的改變量以及中心剛體角速度均趨于穩定值，而考慮剛-柔=熱耦合效應時，以上變量均趨于不穩定。由于太陽帆板產生熱變形的根本原因是內部熱應力的作用，而熱應力是與太陽帆板內部溫度差直接聯系的， 因此，在考慮剛-柔-熱耦合效應時，內部溫度差失穩是導致太陽帆板熱振動失穩的根本原因。

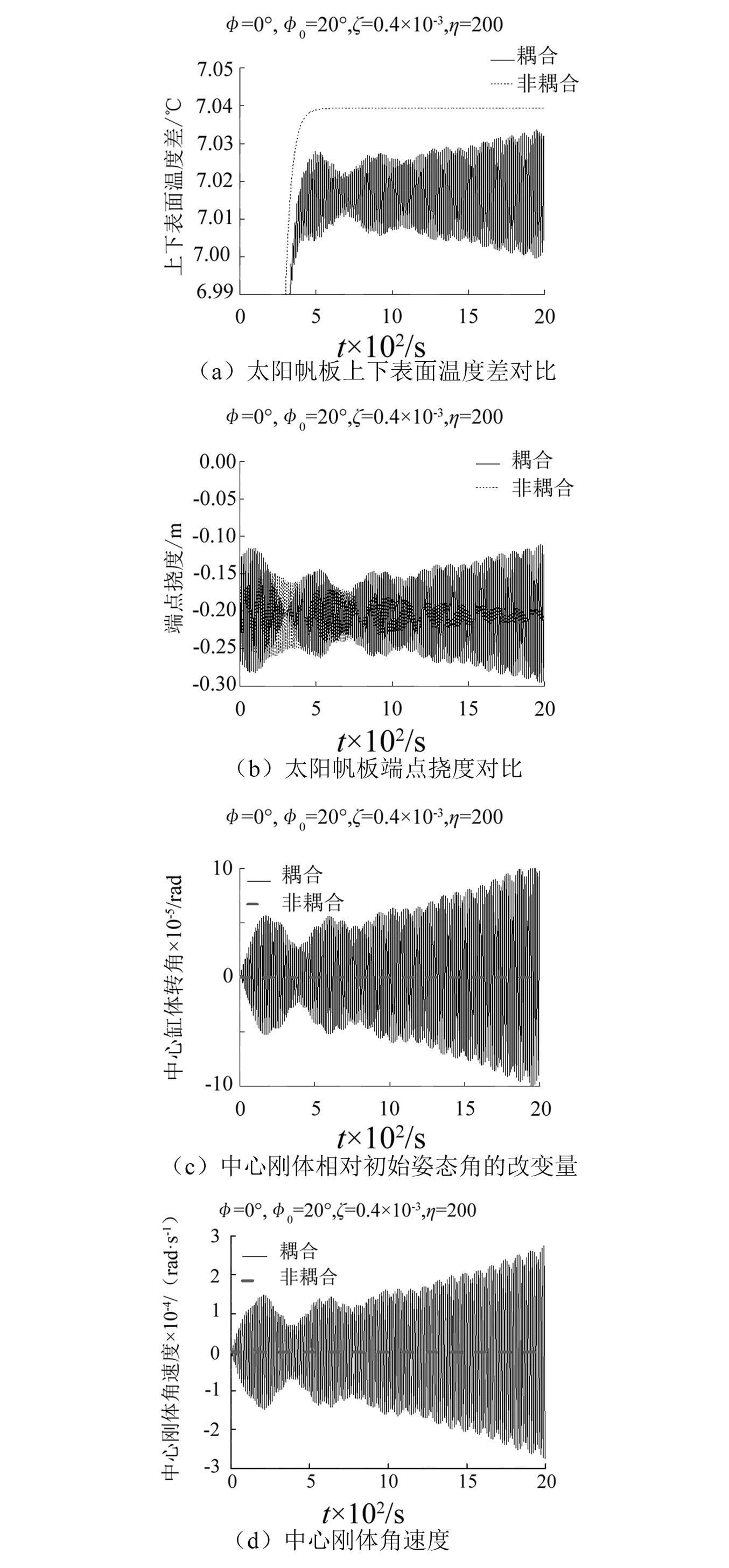
圖6　考慮耦合效應與否對比Fig.6 Comparison of the results obtained by coupling and non-coupling models

4.3綜合熱流與太陽直接輻射熱流影響對比分析

如圖7所示，表示衛星處于φ=0°，初始姿態角φ0=20°，太陽帆板阻尼系數ζ=0.67×10-3，中心剛體與太陽帆板轉動慣量之比η=200時，只考慮太陽直接輻射熱流與考慮綜合熱流的衛星熱運動情況對比。由圖可知，在此種參數下，只考慮太陽直接輻射時，太陽帆板上下表面溫度差、太陽帆板端點撓度、中心剛體相對初始姿態角的改變量以及中心剛體角速度均趨于穩定值趨于穩定值，而考慮綜合熱流影響時，以上變量均趨于不穩定。由此可見，對低軌道運行的航天器，在計算熱穩定性區域時有必要考慮地球反照輻射熱流以及地球紅外輻射熱流的影響。

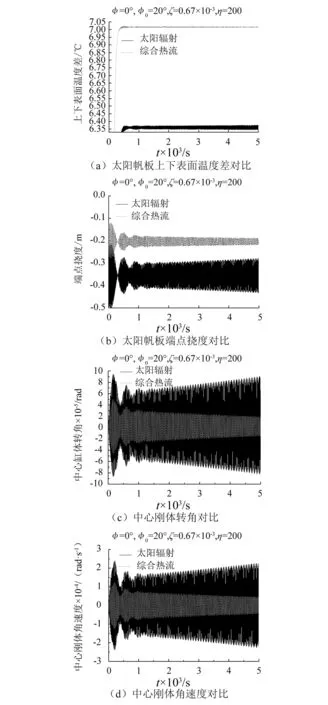
圖7　只考慮太陽直接輻射熱流與考慮綜合熱流情況對比Fig.7 Comparison of the results considering only solar heat flux and those considering all the heat flux

4.4系統熱振動影響因素分析

針對衛星中心剛體與太陽帆板不同轉動慣量之比，研究衛星不同初始姿態角時阻尼系數的穩定性區間，得出以下衛星-太陽帆板熱振動的穩定性區間，見圖8。

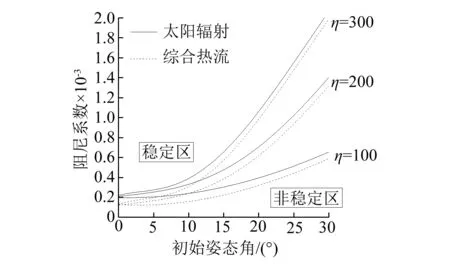
圖8　不同轉動慣量比的穩定性區間Fig.8 Stable region for satellite of different moment of inertia

圖8橫坐標表示衛星的初始姿態角，縱坐標表示太陽帆板的阻尼系數，圖中曲線表示衛星位于(太陽和地球連心線上)時，中心剛體與太陽帆板轉動慣量之比為100、200、300，只考慮太陽直接輻射熱流與綜合考慮三種熱流輻射時太陽帆板熱振動的臨界阻尼，曲線上方表示太陽帆板熱振動穩定性區間。由圖可知，衛星初始姿態角越大、太陽帆板阻尼系數越小，中心剛體轉動慣量越大，系統穩定性區間越小，越容易發生不穩定熱振動；對比只考慮太陽直接輻射熱流和綜合考慮太陽直接輻射熱流、地球反照輻射熱流以及地球紅外輻射熱流的情況可以發現，后者的穩定性區間更大。由圖5可知，與只考慮太陽直接輻射熱流相比，綜合考慮各種熱流時太陽帆板對日面和背日面接受到的熱流密度之差較小，導致內部溫度差變化較小，產生的熱應力應變也較小，因而穩定性區間更大。

5　結　論

本文以低軌道下運行的衛星-太陽帆板系統為研究對象，考慮了除太陽直接輻射熱流以外的地球紅外輻射熱流以及地球反照熱流的影響，同時考慮了太陽帆板熱變形衛星的熱振動與熱流之間的耦合作用，建立了太陽帆板的有限元離散熱傳導方程，引入熱彈性應力應變關系，利用虛功原理，Jordan速度變分原理，引入系統約束方程，應用拉格朗日第一類方程，建立了系統的考慮熱效應的動力學方程。熱傳導方程包含太陽帆板熱變形及衛星熱運動相關量，而動力學方程包含太陽帆板溫度等熱力學參數，因而需要將方程聯立求解，即構成了完整的剛-柔-熱耦合系統方程。

對某一給定參數的衛星進行仿真計算，首先比較了綜合熱流與太陽直接輻射熱流之間的大小關系，發現相對于太陽直接輻射熱流，地球紅外輻射熱流以及地球反照熱流對太陽帆板背日面的影響較大，而對太陽帆板對日面影響不大；進而對衛星熱振動穩定性進行了分析，發現在某些情況下，如果不考慮耦合效應或者只考慮太陽直接輻射，將會得出錯誤的穩定性結論；然后對衛星中心剛體與太陽帆板轉動慣量之比、衛星初始姿態角以及太陽帆板阻尼系數的數值仿真分析，得出初始姿態角越小、太陽帆板阻尼系數越大，中心剛體轉動慣量越小，系統穩定性區間越大，越不容易發生不穩定熱振動。

本文在在研究低軌道下運行的衛星時，相比于前人工作，除了考慮太陽直接輻射熱流，還考慮了地球紅外輻射熱流以及地球反照輻射熱流，研究系統的整體運動時，考慮太陽帆板的熱變形、衛星的熱運動與熱流之間的耦合效應，即衛星-太陽帆板的剛-柔-熱耦合效應，模型更加接近衛星的實際運動狀態，因而提出的建模方法和仿真結果也更加具有工程參考價值。

[ 1 ] 秦文波,程惠爾,李鵬.航天器剛性基板太陽電池陣在軌熱分析[J]. 哈爾濱工業大學學報, 2008, 40(5): 827-831. QIN Wenbo, CHENG Hui’er, LI Peng. Thermal analysis of solar array with rigid substrate on spacecraft in orbit [J]. Journal of Harbin Institute of Technology, 2008, 40(5): 827-831.

[ 2 ] LI J, YAN S, CAI R. Thermal analysis of composite solar array subjected to space heat flux [J]. Aerospace Science and Technology, 2013, 27(1): 84-94.

[ 3 ] 喬博. 柔性太陽電池陣單翼板溫度場分布數值分析[D]. 哈爾濱：哈爾濱工業大學， 2014.

[ 4 ] 孔祥宏,王志瑾.空間站柔性太陽翼桅桿熱誘發振動分析[J]. 上海交通大學學報, 2014, 48(8): 1103-1108. KONG Xianghong, WANG Zhijin. Thermally induced vibration of the flexible solar wing of the mast of space station [J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1103-1108.

[ 5 ] 孔祥宏,王志瑾.空間站柔性太陽翼熱誘發振動分析[J]. 振動與沖擊, 2015, 34(5): 220-227. KONG Xianghong, WANG Zhijin. Thermally induced vibration analysis of a space station’s flexible solar wing [J]. Journal of Vibration and Shock, 2015, 34(5):220-227.

[ 6 ] 楊癸庚,朱敏波,連培園,等.大型可展開天線與衛星的熱致耦合動力學分析[J]. 振動與 沖擊, 2014, 33(24): 173-178. YANG Guigeng, ZHU Minbo, LIAN Peiyuan, et al.Thermal induced coupling-dynamic analysis of a deployable satellite antenna system [J]. Journal of Vibration and Shock, 2014, 33(24): 173-178.

[ 7 ] JOHNSTON J D, THORNTON E A. Thermally induced dynamics of satellite solar panels [J]. Journal of Spacecraft and Rockets, 2000, 37(5): 604-613.

[ 8 ] THORNTON E A, KIM Y A. Thermally induced bending vibrations of a flexible rolled-up solar array [J]. Journal of Spacecraft and Rockets, 1993, 30(4): 438-448.

[ 9 ] 薛明德,李偉,向志海.中心艙體-附件耦合系統熱顫振有限元分析[J].清華大學學報(自然科學版),2008,48(2):270-275. XUE Mingde, LI Wei, XIANG Zhihai. Thermal flutter analysis of a spacecraft with a flexible appendage based on FEM [J]. Journal of Tsinghua University (Science and Technology), 2008, 48(2): 270-275.

[10] 王捷,劉錦陽.剛-柔-熱耦合多體系統的動力學分析[J].應用力學學報,2012(5):501-507. WANG Jie, LIU Jinyang. Dynamic analysis of the rigid-flexible-thermal Coupling systems [J]. Chinese Journal of Applied Mechanics, 2012(5): 501-507.

[11] 吳江,趙治華,任革學,等. 多體動力學熱-結構耦合圓管單元及其應用[J]. 工程力學, 2013, 30(11): 28-35. WU Jiang,ZHAO Zhihua, REN Gexue, et al. Thermal-structural coupled tube element of multibody dynamics and its application [J]. Engineering Mechanics, 2013, 30(11): 28-35.

[12] SHEN Z, TIAN Q, LIU X, et al. Thermally induced vibrations of flexible beams using absolute nodal coordinate formulation[J]. Aerospace Science and Technology, 2013, 29(1): 386-393.

[13] 金學寬.近地航天器受照角系數的矢量計算法[J].宇航學報,1984,1(7):69-80. JIN Xuekuan. A vector method for calculating received radiation angle coefficient of nearearth spacecraft [J]. Journal of Astronautics, 1984, 1(7):69-80.

[14] 樊偉.考慮多場耦合的多體系統動力學[D].上海：上海交通大學,2013.

[15] 劉錦陽,洪嘉振.剛-柔耦合動力學系統的建模理論研究[J].力學學報,2002(3)：408-415. LIU Jinyang, HONG Jiazhen. Study on dynamic modeling theory of rigid-flexible coupling systems [J]. Acta Mechanica Sinica, 2002(3)： 408-415.

Rigid-flexible-thermal coupling dynamic modeling a satellite-solarpanels system in low earth orbit

ZUO Yashuai, LIU Jinyang

(School of Naval architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

In the conventional dynamic modeling for satellite-solar panels systems, for considering the thermal effect, only the heat flux by direct solar radiation is taken into account, which cannot be extended to satellite-solar panels systems in low earth orbit. In the paper, a general modeling method for analyzing the rigid-flexible-thermal coupling dynamic performance of a satellite-solar panels system in low earth orbits was proposed. The expressions for the heat flux of direct solar radiation, earth infrared radiation and reflected solar radiation by the earth were derived considering the coupling relationship among the thermally induced deformation of panels, attitude motion of satellite and the heat flux caused by different kinds of thermal radiations. Assuming the satellite-solar panels system as a hub-beam multibody system, the heat conductive equation of a cantilevered beam was derived, and then by leading in the thermal stress-strain relationship, dynamic equations of the satellite-solar panels system were obtained based on the principle of virtual work. The heat conductive equation and the dynamic equations were solved simultaneously. A simulation analysis of the satellite-solar panels system was carried out to show the influences of the earth infrared radiation and reflected solar radiation by the earth on the thermally induced vibration. In addition, the influence of considering the rigid-flexible-thermal coupling effect on the dynamic performance of the flexible multibody system was revealed. Finally, the stable regions of some parameters affecting the thermally induced vibration were given.

satellite-solar panels in low orbit, rigid-flexible-thermal coupling dynamics, thermally induced vibration

國家自然科學基金資助(11272203；11132007)

2015-09-17修改稿收到日期：2016-02-06

左亞帥 男，碩士，1991年7月生

劉錦陽 女，博士，教授，1964年9月生

O313.7

A

10.13465/j.cnki.jvs.2017.06.006