基于聲傳感器陣列的連續泄漏定位方法研究

邊 旭， 張 宇， 王佳強， 李一博， 靳世久， 孫立臣， 綦 磊

(1.天津大學 精密測試技術與儀器國家重點實驗室，天津 300072; 2.北京衛星環境工程研究所, 北京 100094)

基于聲傳感器陣列的連續泄漏定位方法研究

邊 旭1， 張 宇1， 王佳強1， 李一博1， 靳世久1， 孫立臣2， 綦 磊2

(1.天津大學 精密測試技術與儀器國家重點實驗室，天津 300072; 2.北京衛星環境工程研究所, 北京 100094)

針對壓力容器(如在軌航天器)發生泄漏時的漏孔定位問題進行研究，提出了一種基于聲傳感器陣列的定位方法。當已發生泄漏時，該方法通過聲傳感器陣列獲取器壁中傳播的超聲波信號，并分析陣列中各個傳感器采集數據間的時空相關性，實現了對泄漏源的快速準確定位。分析了泄漏所激發的超聲波信號在薄板中的傳播特性，證明了采集信號相關性隨采集點間距離的增大而減小，從而指導傳感器陣列的設計與制作，同時通過設計相應的實驗討論了不同陣元間距條件下的定位精度。實驗結果表明定位誤差受陣列中陣元數目及陣元間間距影響，當陣元數目為8，陣元間距為8 mm情況下，本算法在1 m2的平板上，定位絕對誤差平均值小于10 mm。

超聲；泄漏；定位；陣列傳感器

氣體泄漏對于密閉系統(如真空熱處理爐，在軌航天器等)存在嚴重的危害，其一旦發生會直接影響設備及人員的安全，造成經濟損失。當泄漏發生時需要一種實時在線的檢測手段對泄漏源進行快速有效定位，減少經濟、人員損失。

目前對于大型容器泄漏，例如在軌航天器泄漏，普遍采用壓降法進行檢測，當容器氣壓下降則容器發生泄漏，但此種方法不能對泄漏源進行定位。NASA與其他公司聯合研制的CTRL系統可以實現對泄漏源的定位[1]。其由耳機和超聲探測器兩部分組成，使用時用超聲探測器在可疑的部位進行探索，如果有泄漏存在，超聲探測器能夠檢測到泄漏產生的超聲波，并將超聲波轉化為人耳能聽到的聲音并傳到耳機中，操作者通過耳機中的聲音來判斷有泄漏存在。此種設備對泄漏不能實現實時定位，定位耗時長，并不適用于大型容器的檢漏，且由于人工的引入導致定位精度不佳。需要高精度的定位，通常應用氦質譜儀檢測法[2]。氦質譜檢漏法依據質譜學原理，利用氦氣作示漏氣體進行氣密性檢測，優點是本底噪聲小、氦氣本身安全無污染、檢測靈敏度高，但氦質譜檢漏工藝復雜，在面向大型結構部件時難以實現對泄漏源的快速定位，只適合做驗證性檢測；也不能實現對泄漏源的在線檢測[3]。DAVOODI等[4]基于小波變換、濾波和互相關技術， 提出了一種應用于管道氣體泄漏的泄漏定位算法，定位誤差小于5%。劉貴杰等[5]對閥門內漏產生的聲發射現象進行了研究，嘗試利用EEMD和HHT變換對聲發射特征信號處理并提取閥門內漏聲發射信號的特征。何田等[6]提出了一種利用聲發射波束形成法的旋轉機械轉靜子碰摩故障定位的方法，該方法可成功的識別出突發型碰摩故障位置。沈功田等[7]基于聲學的方法和相關定位原理開發研制了一種管道泄漏點定位的檢測儀，該儀器利用專用低頻傳感器對泄漏聲信號進行采集，可對不同材質和不同介質的管道泄漏進行定位。HOLLAND 等[8-9]針對連續泄漏源，提出應用8×8傳感器陣列采集聲信號，通過計算獲得平面波數場強度分布圖，以估計聲源方向，同時應用不同位置上兩組定向結果實現對泄漏連續聲發射信號實時定位。但此種方法需要對64陣元數據進行分析處理，對系統要求較高，且定位精度并不十分理想。本文從實用角度出發，提出了一種基于陣列傳感器的定位方法，其結構簡單，系統成本較低且容易實現，可以解決大型器壁，如航天器在軌條件下泄漏的實時快速定位需求。

1 定位原理

實際應用中，對時域特征明顯的信號可以通過傳統的聲達時間差法(TDOA)進行定位，該方法通過分辨泄漏所激發的聲發射信號到達各個采集點的時間差，從而實現對泄漏源的定位[10]。但對于連續泄漏信號并不存在明顯的時域特征。根據氣體動力聲學理論，壓力容器一旦發生氣體泄漏，由泄漏孔流出(流入)的高速氣流形成湍流射流，泄漏導致氣體不規則運動并激發了大量隨機的聲波信號[11]。其時域表現為噪聲信號，并無明顯規律。

基于泄漏所激發的超聲信號特點，本文選擇L型陣列傳感器實現對泄漏源的定向，其特性可參考文獻[12-15]。實際應用中通過綜合多組L型陣列傳感器定向結果實現對器壁任意位置泄漏源的快速定位。定位原理圖如圖1所示。

圖1中，以N+m個傳感器所組成的L陣列為例，ai為第i個傳感器距離參考傳感器(算法中默認為1號傳感器)距離，聲速為c，聲源與基準偏移角度為Δθ，兩陣列坐標分別為(x1,y1)，(x2,y2)。根據幾何關系，聲源位置(x,y)符合以下關系：

圖1 定位原理圖Fig.1 Location principle diagram

y-y1=tan(2π-Δθ1)(x-x1),

y-y2=tan(2π-Δθ2)(x-x2)

(1)

實際應用中傳感器位置坐標已知，故定位算法可以簡化為對兩組傳感器Δθ參數的求取。同一泄漏源信號在時域上穩定存在且相關，所以利用傳感器陣列采集空間信號，通過計算所采集信號陣列空間及時間上相關性最大方向，從而達到估計泄漏方向的目的。

設第i號陣元傳感器采集到的信號為pi(t),i=1,2,…N+m，令

(2)

在θ方向上，第i號傳感器所在位置相對于參考傳感器所在位置信號傳播時間可用式(3)表示。

i=N+1,N+2,…,N+m

(3)

由于在薄板中超聲波以Lamb波形式傳播，存在明顯頻散現象，故聲速c為關于頻率的函數。根據前期工作證明[16]在所涉及的頻帶(100～500 kHz)及板厚條件下，超聲傳感器接收到的信號主要為A0模態，其余模態可忽略，則將c寫為cA0(f)。則：

(4)

將所有延時Δti(θ,f)用矩陣形式表示，則寫為：

T(θ,f)=[Δt1(θ,f),Δt2(θ,f),…,ΔtN+m(θ,f)]

(5)

選取時間窗口(ta,tb)，以及頻帶(fc,fd)，綜合式(2)及式(5)，在特定角度θ下，傳感器陣列輸出能量函數(E)可寫為：

(6)

數學上可以證明上式僅當θ=Δθ時，即估計方向與來波方向一致時，E取得最大值。證明過程可參考[16]。通過MATLAB軟件對算法進行編寫，對陣列傳感器采集信號進行分析，其輸出能量與θ關系圖(見圖2)。

圖2 能量(相對)與角度關系圖Fig.2 Angle-power relation diagram

2 聲傳感器陣列設計

根據式(4)與式(6)可得，傳感器陣列參數ai和N+m均對E取值有影響，從而影響算法定向精度。故需要對傳感器陣列參數取值進行討論。

2.1 陣元間距的選取

本文提出算法基于陣列采集信號相關性進行討論，式(6)中計算E時需要保證pi(t),i=1,2,…,N+m,具有一定的相關性，數學證明過程可參考[13]。但實際上超聲波在非理想器壁中傳播時，會受到器壁上其它結構(如焊縫，加強筋等)的影響；同時由于其在器壁中主要以Lamb波方式傳播，存在明顯的頻散現象[17-18]，使得傳播規律更為復雜，導致對同一泄漏源激發的信號在板中不同位置采集時相關性變差，需要進一步研究。故本文選用Polytec PSV-500型激光多普勒測振儀進行實驗，該系統可以非接觸式的實現對物體表面任意質點振動情況快速精確的測量，保證各個采集點信號采集時實驗條件的一致性。通過分析采集數據得到ai對pi(t),i=1,2,…N+m,間相似度變化的影響，為傳感器陣列的設計與制作提供依據。實驗平臺搭建見圖3。

圖3 激光多普勒測振儀實驗平臺Fig.3 Laser vibrometer experimental platform

實驗母版采用5A06型鎂鋁合金材料，實驗中將實際采集到的泄漏信號輸入可編程信號發生器，通過耦合在板上的超聲換能器進行激發以模擬泄漏聲源，并且通過設置同步脈沖使得采集和激發時間同步，保證各個采集點所采集的原始信號一致。實驗時通過調整采集點坐標實現對不同間距樣本的采集，同時利用測振儀對板中不同位置進行掃描，使得各個間距樣本數據具有普遍性。以某次實驗為例，采樣率為3.125 MHz，其掃描示意圖見圖4。

圖4 實驗掃描示意圖Fig.4 The scanning schematic diagram

其中1～14代表激光多普勒測振儀掃描點，掃描區域A、B中的采樣點擁有相同的空間分布，以1、2號位置為例，其間距為6 mm，選取時間長度為0.03 s的數據進行分析，應用MATLAB軟件對其時域振動信號進行互相關運算，得到相關系數曲線，如圖5所示。

圖5 1、2號位置實際采集信號相關性曲線Fig.5 Correlation curve of the signals form position No.1 and No.2

圖5中可得1、2號位置上信號相關系數最大值為0.504 6。應用相同方法對板中不同位置，不同間隔條件下信號相關性進行分析統計得到如下表。表中所得結果均為在不同位置下所得結果的統計值，具有一般性。

根據表1，所采集信號的相關性隨著采集點間距的增大而逐漸減小。而另一方面，根據式(4)所示，當ai變小時Δti(θ,f)會相應的減小，為了保證結果的精度，需要系統擁有更高的采樣率和檢測靈敏度。故綜合考慮以上兩點，實際應用時選取陣元間距為8 mm。

表1 不同間距下信號相關性統計Tab.1 The statistics of the correlation in different spacing

2.2 陣列中陣元數目

根據式(6)可得，增大N+m取值時，可以提高傳感器陣列定向精度及穩定性。為了獲得N+m取值與定向精度的關系，將不同陣元數的傳感器陣列相對某一聲源依次按順序旋轉固定角度，并計算此時對此聲源的定向誤差。以ai=8 mm陣元間距陣列為例，旋轉角度為5°，實際實驗結果，如圖6所示。

圖6 傳感器陣列中陣元數量對定向精度的影響Fig.6 The relationship of the directional accuracy and the number of the sensors in the sensor array

根據實驗數據統計，當傳感器數量過少時(少于6個)其誤差明顯增大。故本文綜合定向精度需求以及實際應用開銷，采用8只聲發射傳感器組成L型傳感器陣列。

根據以上討論，最終傳感器單元采用PAC(美國物理聲學公司)nano30型傳感器，其直徑為8 mm，可以保證陣列具有良好的空間響應，其詳細參數可參考PAC產品手冊。應用8個此種傳感器組成傳感器陣列如圖7所示。

3 定位實驗設計

通過設計相應實驗，以驗證所設計傳感器陣列定向性能及算法定位精度。選用5A06鎂鋁合金作為材質，加工成長寬為1 m×1 m，厚度為2.5 mm的平板以模擬泄漏器壁。板上在不同位置預先打下特定孔徑(1～2 mm)的圓形孔模擬發生泄漏的泄漏孔。以真空泵、真空波紋管等提供氣體泄漏條件，實驗平臺原理圖如圖8所示。

圖8 實驗平臺原理圖Fig.8 The schematic diagram of the experimental apparatus

實驗所用聲發射儀器為全數字16通道聲發射檢測系統DS2-16A。可實現3 MHz采樣率的8路同步采集。真空泵通過真空吸嘴與泄漏孔相連，如圖9所示，通過真空泵產生壓差以模擬泄漏工況。將傳感器陣列用真空脂耦合放置在實驗板上，并通過前置放大器(增益為40 dB)與聲發射儀相連，最終將多路采集數據傳輸到電腦上進行處理。

圖9 真空吸嘴Fig.9 Vacuum nozzle

4 結果與討論

以泄漏孔在實驗平板中心為例，漏孔大小為1 mm。通過陣列傳感器以3 MHz采樣率采集泄漏時域信號，采集時長為0.01 s，以陣列中1號傳感器采集信號為例，根據計算需求對其進行100～500 kHz帶通濾波后，其時頻圖(見圖10)。

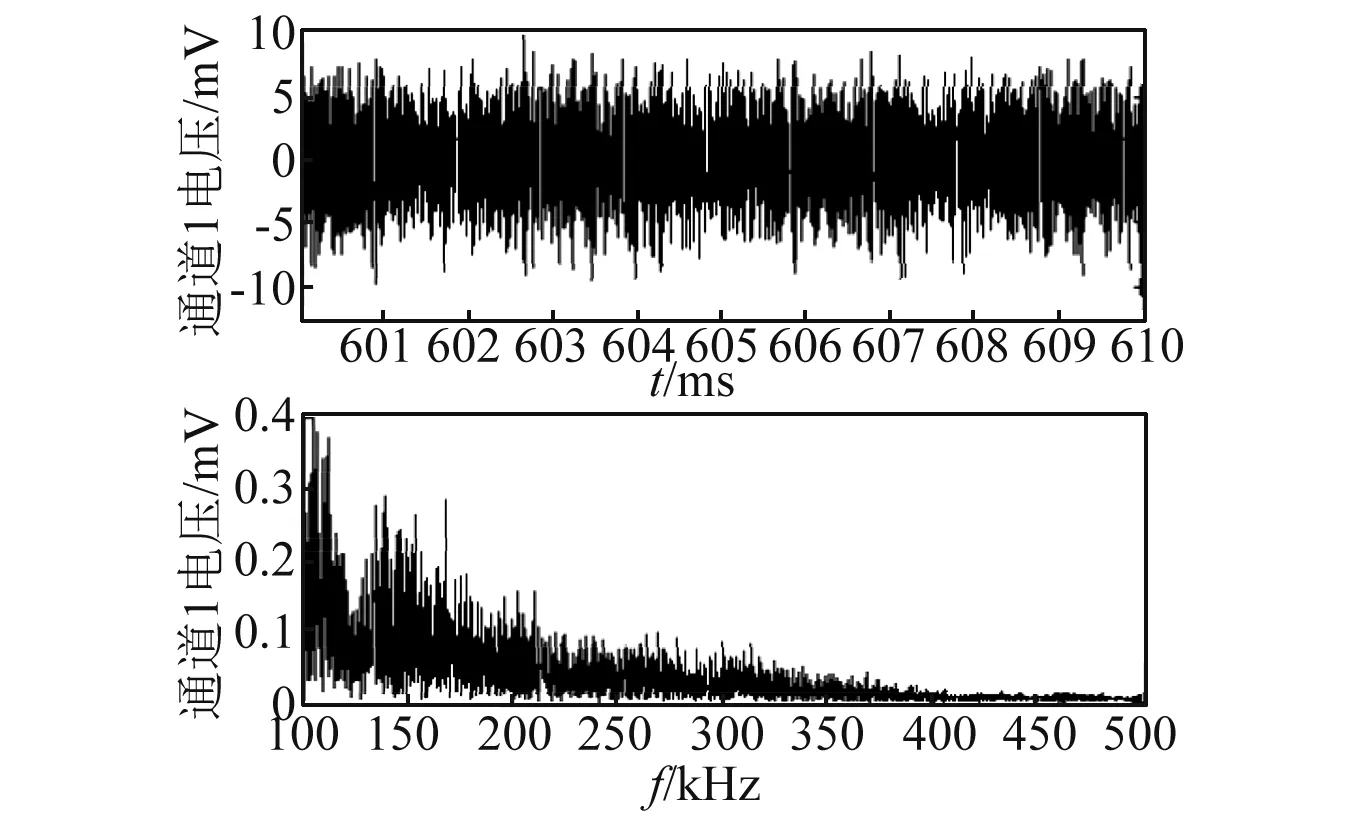
圖10 傳感器采集泄漏信號時頻圖Fig.10 The signal time-frequency diagram

如圖10所示，泄漏信號為寬帶信號，且隨著頻率增高信號能量衰減增大。同時其時域上并無明顯特征，進一步對該信號在不同時刻自相關性進行計算，典型自相關曲線如圖11所示。

圖11 泄漏信號自相關Fig.11 Self-correlation of the signal

從自相關結果可得，同一泄漏源所激發的超聲波信號在不同時刻不相關，屬于隨機信號。將傳感器陣列布放在實驗板上兩個不同位置，并將各個陣列中傳感器同步采集數據導入MATLAB軟件進行計算處理，最終得到不同位置定向結果如圖12所示(左邊為笛卡爾坐標表示，右邊為極坐標表示)。

從角度-能量圖中我們可以看到，曲線存在明顯的最大值。在曲線中能量最大點所對應的角度即為泄漏源相對基準線夾角方向。為避免擺放誤差，真實角度均經過高精度數顯量角器測量。綜合兩次定向結果可得到實際定位結果，如圖13所示。經過計算，本次定位誤差為9.7 mm(估計點與實際漏孔距離差)。在實驗板上建立直角坐標系以供參考(圖中單位為cm)。

(a) 1號位置

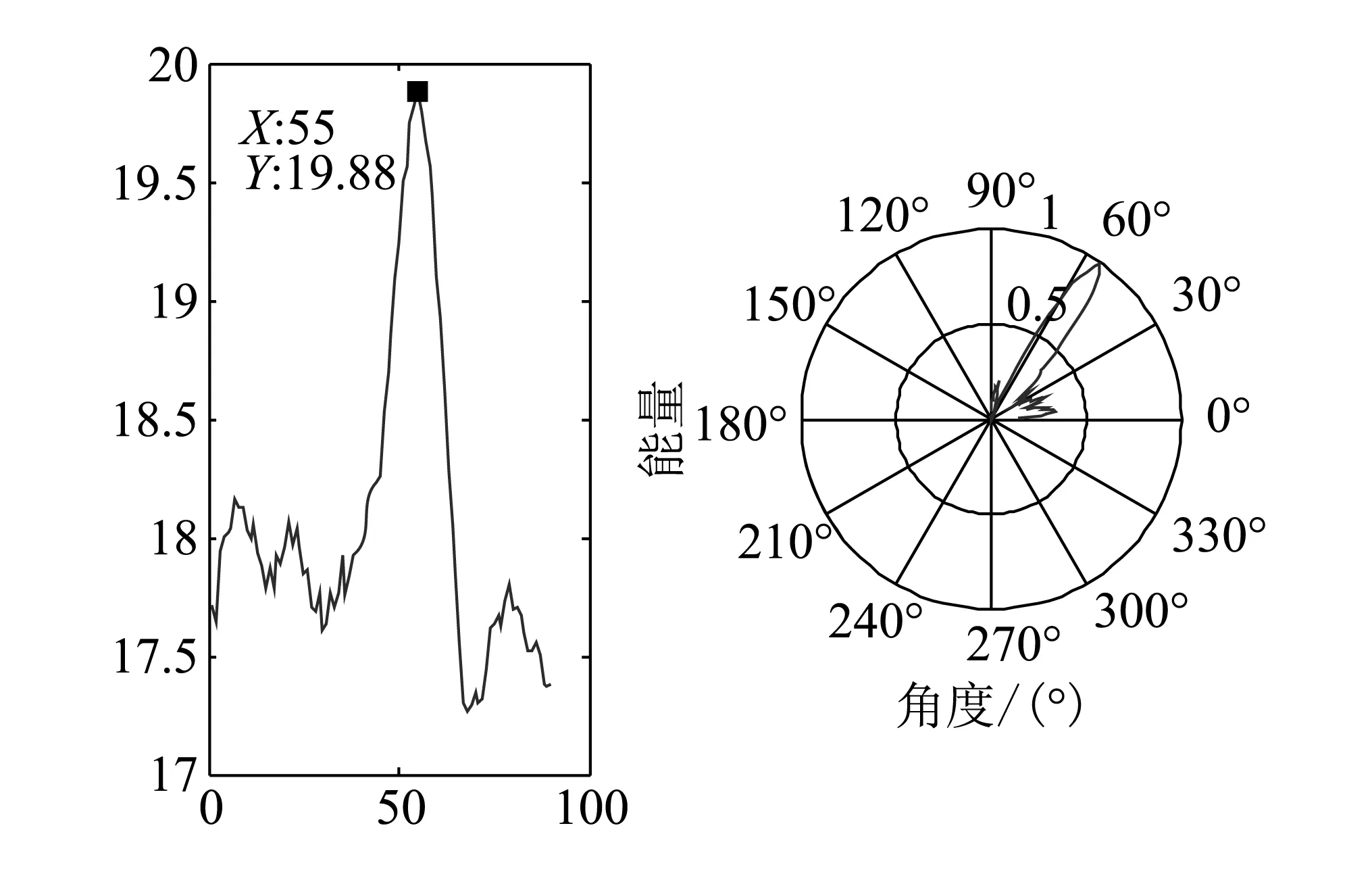
(b) 2號位置圖12 定位結果Fig.12 The location results

圖13 傳感器陣列擺放位置示意圖Fig.13 The spacing diagram of the sensor array

按照此方法，我們進行了一系列實驗討論在不同陣元間距條件下的算法性能。將兩組傳感器陣列隨機布放在實驗板不同位置，分別對板中不同位置漏孔進行定位實驗，并保證實驗條件不變的情況下，改變陣列中陣元間距作為對比項，分別選取其中50組實驗樣本為例，定位誤差結果歸納如圖14所示。

圖14 不同陣元間距條件下的定位誤差Fig.14 The location error under different distances between the sensors in the array

定位誤差定義為估計點和實際泄漏點之間的距離，從圖中我們可以看出，當陣列中陣元間距增大時，定位誤差隨之增大，與第3節分析結果一致。當陣元間間隔為8 mm時，本文定位方法定位誤差絕對值小于10 mm組為98%，絕對誤差平均值為3.42 mm，方差為24.4。可以在較低的系統要求下，獲得較高的定位精度及穩定性，滿足實際應用精度需求。

5 結 論

(1) 泄漏激發的超聲波信號為連續寬頻隨機信號，根據Lamb理論，其在薄板中以Lamb波形式傳播，存在明顯的頻散現象，傳播規律較為復雜。實驗結果表明，在實際情況下傳感器陣列中各陣元采集信號相關度會隨著陣元間距的增大而減小，信號空間相關性信息減少，導致定位結果準確率降低。

(2) 本文基于聲傳感器陣列實現了一種實用性較高的高精度泄漏定位方法，并對相應的傳感器陣列進行了設計與制作，有效解決孔徑在1 mm及以上漏孔泄漏在線定位問題。實驗表明，在1 m×1 m×2.5 mm平板條件下，定位平均誤差小于10 mm。為解決大型容器(如在軌航天器)氣體泄漏檢測定位提供了一種新的方法。

[ 1 ] WILSON W C, COFFEY N C, MADARAS E I. Leak detection and location technology assessment for aerospace applications [R]. NASA/EM-2008-215347.

[ 2 ] BUILO S I. Acoustic-emission diagnostics of the effect of hydrogen on properties of materials [J]. Russian Journal Nondestructive Testing, 2009, 45 (11): 818-821.

[ 3 ] MURVAY P S, SILEA I. A survey on gas leak detection and localization techniques [J]. Journal of Loss Prevention Process Industries, 2012, 25 (6): 966-973.

[ 4 ] DAVOODI S, MOSTAFAPOUR A. Gas leak locating in steel pipe using wavelet transform and cross-correlation method [J]. International Journal of Advanced Manufacturing Technology, 2014, 70: 1125-1135.

[ 5 ] 劉貴杰，徐萌，王欣，等. 基于HHT的管道閥門內漏聲發射檢測研究[J]. 振動與沖擊，2012, 31(23): 62-66. LIU Guijie, XU Meng, WANG Xin， et al. AE detection for pipeline valve leakage based on HHT [J]. Journal of Vibration and Shock, 2012, 31(23): 62-66.

[ 6 ] 何田, 劉耀光, 陳亞農,等. 基于聲發射波束形成法的轉靜子碰摩故障定位[J]. 航空動力學報, 2011, 26(10):2207-2213. HE Tian, LIU Yaoguang, CHEN Yanong， et al. Method for locating rub fault of rotor-stator based on acoustic emission beamforming [J]. Journal of Aerospace Power, 2011, 26(10): 2207-2213.

[ 7 ] 沈功田, 劉時風, 王瑋. 基于聲波的管道泄漏點定位檢測儀的開發[J]. 無損檢測, 2010(1):53-56. SHEN Gongtian, LIU Shifeng, WANG Wei. Development of pipeline leakage location instrument based on acoustic waves [J]. Nondestructive Test, 2010(1):53-56.

[ 8 ] HOLLAND S D, ROBERTS R, CHIMENTI D E, et al. An ultrasonic array sensor for spacecraft leak direction finding [J]. Ultransonics, 2006, 45(1/2/3/4): 121-126.

[ 9 ] HOLLAND S D, ROBERTS R A, CHIMENTI D E. Leak detection in spacecraft using structure-borne noise with distributed sensors [J]. Applied Physics Letters, 2005, 86:1-4.

[10] LOMBARD A. TDOA estimation for multiple sound sources in noisy and reverberant environments using broadband independent component analysis [J]. Audio, Speech, and Language Processing, 2011(6):1490-1503.

[11] ROSE J L. Ultrasonic waves in solid media [M]. Cambridge: Cambridge University Press, 2004.

[12] VAN TREES H L, HARRY L. Optimum array processing: part IV of detection, estimation, and modulation theory [M]. New York: John Wiley and Sons Inc, 2002.

[13] VAN TREES H L. Optimum array processing. Part IV of detection, estimation, and modulation theory [M]. New York: John Wiley and Sons Inc, 2002.

[14] HUA Y, SARKAR T K, WEINER D D. An L-shaped array for estimating 2-D directions of wave arrival [J]. IEEE Trans Antennas Propagation, 1991, 39: 143-146.

[15] ZHANG X, LI J, XU L. Novel two-dimensional DOA estimation with L-shaped array [J]. EURASIP Journal of Advances Signal Processing, 2011, 1:1-7.

[16] BIAN Xu, ZHANG Yu, LI Yibo, et al. A new method of using sensor arrays for gas leakage location based on correlation of the time-space domain of continuous ultrasound [J]. Sensors, 2015, 15(4): 8266-8283.

[17] KUNDU T, NAKATANI H, TAKEDA N. Acoustic source localization in anisotropic plates [J]. Ultrasonics, 2012, 52 (6): 740-746.

[18] PETERSON D A. Acoustics: an introduction to its physical principles and applications [M]. New York: Acoustical Society of America, 1989.

Leakage location method based on an ultrasonic sensor array

BIAN Xu1， ZHANG Yu1， WANG Jiaqiang1， LI yibo1, JIN Shijiu1， SUN lichen2, QI Lei2

(1. State Key Laboratory of Precision Measurement Technology and Instrument，Tianjin University，Tianjin 300072, China;2. Vacuum and Leak Detecting Division Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

Based on an ultrasonic sensor array, a method for leakage location of pressure containers (such as spacecraft) was proposed. When the leaking happens, the method could accomplish the fast and accurate location of leakage source through acquiring a set of ultrasonic signals on the wall of container by using an ultrasonic sensor array,and analyzing the time-space correlation among all the data collected by each sensor in the array. Moreover, the propagation characteristics of leakage signals in a thin plate were analysed. It proves that the correlation between the collected signals will decrease as the distances between the collection points increase, which provides a reference to the design of sensor arrays. Meanwhile, the related experiments were designed to discuss the location accuracy of different sensor arrays with different distances between the sensors in the array. According to the experimental results, the location error is influenced by the number of sensors and the distances between them in the array. When the number of sensors in the array is eight, and the distances between them are 8 mm, the mean value of the absolute location error is less than 10 mm on a one square meter plate.

ultrasound; leakage; location; array sensor

國家青年基金項目(61201039)； 北京衛星環境工程研究所研發課題(YY-BZ(WM)-2013-07)

2015-10-30 修改稿收到日期： 2016-02-04

邊旭 男，博士生，1985年11月生

張宇 男，博士，講師，1982年4月生

TB553；TB771

A

10.13465/j.cnki.jvs.2017.07.020