固定床內壓降的CFD分析

王春雷，王日杰，楊曉霞，喬勝超

(天津大學化工學院，天津 300072)

固定床技術具有結構簡單、操作方便和費用低廉等優點，廣泛應用于化學反應、組分分離和提純等工藝過程。決定固定床技術的性能參數有很多，其中壓降對物料流體進入固定床的動量要求及其對床層內的流體流動、傳熱以及傳質過程的影響非常大，準確預測床層壓降對于固定床的設計與操作都有十分重要的意義。影響床層壓降的因素主要有物料流體本身和固定床結構兩方面，前者包括密度、黏度、進料流速等；后者包括填充床層的顆粒形狀、粒徑、床層空隙率ε、固定床直徑D與粒徑dp之比D/dp(對應壁面效應)等。

目前研究固定床壓降的方法主要有3種：實驗研究、理論分析和CFD模擬。其中，實驗研究結果是理論分析和CFD模擬的基礎，但由于受到模型尺寸、流場擾動和測量精度的限制，實驗研究的難度往往非常大，比如當D/dp<15時，顯著的壁面效應使實驗測量結果的可靠性大大降低；理論分析的優勢在于其所得結果往往具有普遍意義，能夠清楚地認識各種影響因素，但往往需要對計算對象進行大量的抽象和簡化，才可能得到理論解。

在采用理論分析法研究固定床壓降方面，Reichelt等[1]和Eisflied等[2]的工作被認為對固定床的設計具有很好的指導意義。前者還基于Ergun半經驗公式[3]提出計算固定床壓降的經驗公式[式(1)～式(4)]。

(1)

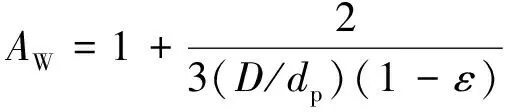
(2)

(3)

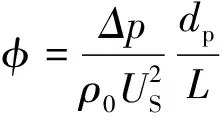
(4)

Eisflied等[2]通過對大量實驗數據進行擬合，給出了式(1)～式(4)中3個常數項K1、k1和k2的精確值，分別為154、1.15和0.87。對于填充單一粒徑的固定床，可直接采用上述半經驗公式[式(1)～式(4)]計算床層壓降；而對于填充不同粒徑的固定床，在采用半經驗公式之前需要確定公式中顆粒直徑的表達形式，Carman[4]引入了有效直徑這一概念，Zeisberger等[5]認為采用數量平均直徑(d10)作為有效直徑得到的壓降預測結果與實驗結果更加吻合；Li等[6]指出在高和低兩種進料流速下，分別可以采用長度平均直徑(d21)和面積平均直徑(d32)來替代有效直徑；Li等[7]發現采用d32替代不同形狀顆粒的有效直徑時，計算得到壓降值非常接近實驗值。

第3種方法，即CFD數值模擬法能夠克服實驗研究和理論分析2種方法的諸多不足。采用CFD法計算流體流動問題，如同在計算機上進行了相應的物理實驗，文獻發現通過合理地建模能夠準確地再現各種流場細節，獲得關于速度場、壓力場和湍流場等豐富的重要信息，而采用實驗法只能通過一些復雜昂貴的大型儀器才能獲得這些信息。很多研究者[8-15]采用實驗法和CFD法研究了固定床內的壓降，模擬結果與半經驗公式或實驗結果基本吻合，并基于這些結果對半經驗公式進行了改進。

但文獻研究的固定床模型的D/dp值一般比較大(D/dp>15)，對小D/dp固定床的研究相對要少得多，而且通常假設填充固定床的顆粒為單一粒徑分布，而實際固定床中的填充顆粒往往服從特定的粒徑分布，如正態分布。鑒于CFD法在研究流體流動以及單相、多相流體系方面的巨大潛力，本研究將采用CFD法分別研究填充單一粒徑以及服從不同粒徑分布的顆粒的小D/dp固定床內的壓降。除此外，考慮到半經驗公式對小D/dp固定床適用性較差，提出更為合理的有效直徑對公式加以改進。

1　CFD建模

1.1　體系和模型

固定床隨機填充單一粒徑和服從特殊粒徑分布的球形顆粒，后者得到的床層為非結構化的，計算量和難度大幅提高。3種粒徑分布如表1所示，d10均為16.5 mm：分布I為單一粒徑；分布II和III為正態分布，標準方差分別為0.4和1.0。對應的3種固定床模型編號分別為I、II和III，固定床直徑和均為0.1 m(D/dp約為6)，床層高度H為0.5 m(H/dp約為30)。

表1　顆粒粒徑分布

采用基于離散元算法的PFC3D軟件實現顆粒的隨機堆放。顆粒之間以及顆粒與壁面之間的相互作用采用Hertz接觸模型。模擬過程涉及參數主要有剪切模量(sh)為8e10，泊松比(po)為0.33，密度(dens)為3 000 kg/m3，摩擦系數(fric)為0.05，阻尼系數(da)為0.2[16]。為確保物理模型的重復性，所有模型均生成3次。

1.2　網格劃分

由于計算模型內部結構復雜，采用適應性更強的非結構化網格。Rep較小時，劃分邊界層以準確捕捉壁面附近的流場細節；而Rep較大時，受網格尺寸的限制，采用“Enhance wall treatment”方法來近似處理壁面附近的流場。網格劃分過程具體詳細參數見表2。為確保獲得與網格數量無關的模擬結果，層流狀態下采用約600萬網格，湍流狀態下采用約500萬網格來劃分計算模型。為避免顆粒之間或顆粒與壁面之間互相接觸而生成高扭曲度網格，在完成建模后將所有顆粒的粒徑均縮減1%。

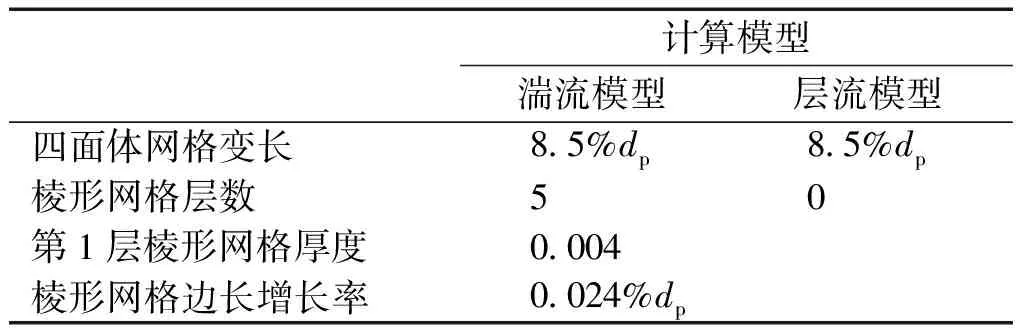
表2　計算域網格劃分方法

1.3　計算條件

模擬過程中選用的物料為空氣，黏度μ=1.7894×10-5Pa·s，密度ρ=1.225 kg·m-3；高湍流狀態下選用的湍流模型為standardk-ε模型；所有壁面為無滑移邊界條件；進口為速度進口邊界條件，進口速度相同，進口與床層之間距離為3dp；出口為壓力出口邊界條件，出口處壓力為101.325 kPa，出口與床層之間距離為7dp。采用SIMPLE算法耦合計算速度場和壓力場，當所有控制方程的殘差小于10-5認為達到收斂。

2　結果及討論

2.1　填充單一粒徑顆粒固定床

2.1.1空隙率

由200個單一粒徑顆粒填充而成的固定床模型I，如圖1所示。

圖1　填充單一粒徑固定床模型Fig.1　Fixed bed model of packed with uniform particles

PFC3D計算得床層空隙率為0.485，這與Theuerkauf等[16]的研究結果基本吻合。為保證PFC3D軟件建立模型的有效性，分析了空隙率沿床層徑向的隨機振蕩變化情況，并與采用De Klerk經驗公式(5)～(7)[17]計算結果進行了比較，如圖2所示。

圖2　2種空隙率分布曲線比較Fig.2　Comparison of two radial profiles for void fraction

通過計算平行于固定床軸線的不同直徑環隙間的床層空隙確定空隙率的徑向分布[18]。

(5)

當z≤0.637時，

ε(r)=2.14z2-2.53z+1

(6)

當z>0.637時,

ε(r)=0.29exp(-0.6z)[cos(2.3π(z-0.16))]

+0.15exp(-0.9z)+εb

(7)

從圖2可以看到PFC3D軟件生成的填充模型的空隙率分布與de Klerk經驗公式[17]得到的空隙率分布基本一致，均呈現為衰減的正弦波。在靠近壁面處，二者幾乎完全相同，在床層中心處，二者略有不同，同時說明采用PFC3D軟件建立的固定床模型合理有效，可以用于CFD模擬研究。

2.1.2壓力分布

采用CFD模擬研究固定床，除了要求建模結構合理以外，還要求模型能夠代表整個床層。圖3展示了低進料速度下固定床內的壓力分布情況。

圖3　床層內壓力分布Fig.3　Pressure distribution in the fixed bed

從圖3中可以清楚地看到在床層上下兩端附近壓力幾乎保持不變，而在床層內部壓力呈線性變化，這說明物料進口和出口距床層的距離已經足夠長，可以忽略進口和出口效應對于固定床內壓力場的影響，同時說明由200個顆粒組成的固定床模型足以代表整個床層，能夠體現床層壓力的整體變化。

2.1.3床層壓降

將固定床進出口壓力差，即壓降ΔP的模擬結果與半經驗公式計算結果進行比較，如圖4所示。

圖4　Rep<120時壓降的CFD結果與半經驗公式結果之間的比較Fig.4　Comparison of pressure drop results between CFD and semi-empirical equation at Rep<120

在低雷諾數(Rep<120)時，CFD模擬結果與Eisflied半經驗公式結果之間的相對誤差較小(<10%)。但隨著Rep的增大，二者之間的相對誤差有所增大(<25%)，并呈現先減小后增大的趨勢(見圖5)。這說明CFD模擬結果與Eisflied半經驗公式均能夠合理地預測單一粒徑固定床床層壓降。

圖5　Rep >120時壓降的CFD結果與半經驗公式結果之間的相對誤差Fig.5　The relative error of pressure drop results between CFD and semi-empirical equation at Rep>120

2.2　填充不同粒徑顆粒固定床

2.2.1空隙率

采用上述方法建立填充不同粒徑顆粒的固定床模型，如圖6所示。由于大顆粒之間的縫隙能夠由小顆粒進行填補，所以固定床模型II和III的總體空隙率相對較小，分別為0.464和0.450。

圖6　填充不同粒徑顆粒固定床模型Fig.6　Fixed bed model packed with different particles

圖7為3種固定床模型的空隙率的徑向分布， 3者均呈震蕩衰減的趨勢。除此外，模型II和III的峰位置向床層中心偏移，粒徑分布標準差越大，該現象越明顯。由于靠近固定床壁面的顆粒受壁面限制而規整排列一側，這使得壁面附近空隙率分布較為規律，即空隙率在離壁面1/2粒徑位置處出現最小值，而1個粒徑位置處達到峰值。

圖7　不同顆粒分布堆積模型中空隙率分布對比Fig.7　Comparison of void fraction profiles in different fixed bed models

從圖7還可以看出靠近壁面處空隙率的第1個峰值位置與壁面之間的距離和顆粒的質量平均直徑(d43)相當，這說明填充顆粒的有效直徑與d43相近。同時為確保模型結果與顆粒堆放位置無關，3種固定床模型均隨機生成3次，模擬結果與上述結果基本一致。

2.2.2粒徑對床層壓降的影響

固定床內空隙率分布會影響流體流動，從而影響床層壓降。在低雷諾數(Rep<120)分別對固定床模型II和III內壓降的CFD模擬結果和Eisflied半經驗公式計算結果進行了比較，如圖8所示。

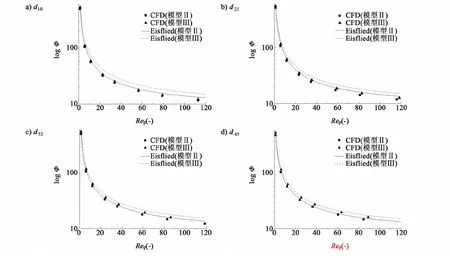
圖8　Rep<120時壓降CFD結果與采用不同平均粒徑的半經驗公式計算結果之間的比較Fig.8　Comparisons of pressure drop results between CFD and empirical equations using different mean diameters at Rep<120

由于固定床內顆粒粒徑不同，需要選擇1個適當的平均粒徑(如d10、d21、d32和d43)來替代原半經驗公式中的粒徑參數。從圖8中可以看出將d43作為平均粒徑代入半經驗公式得到的計算結果與模擬結果之間的偏差最小(<9%)，說明采用d43替代半經驗公式中的粒徑最為合理。固定床結構是決定其床層壓降的一個關鍵因素，而對于小D/dp固定床而言，大粒徑的顆粒對固定床結構的影響較為顯著，因此選用盡量體現大粒徑顆粒作用的平均粒徑來估算床層壓降能夠得到更為準確的計算結果。該結論與文獻結論存在差異，原因可能是本研究的固定床的D/dp較小，大粒徑顆粒足以影響整個床層結構，而對于D/dp較大的固定床，床層中部顆粒的排布受壁面影響較小，處于隨機混亂的堆積狀態，此時顆粒粒徑的大小對其結構影響并不顯著。

高雷諾數(Rep>200)下2種固定床模型內的壓降模擬結果與半經驗公式計算結果之間的相對誤差如圖9所示。

所有相對誤差值普遍較大(>10%)，造成該現象的主要原因是湍流模型[19]和計算網格。當半經驗公式采用d43粒徑時，相對誤差最小。隨著Rep的增大，相對誤差均呈先減小后增大的趨勢，和圖5基本一致。原因可能是當Rep較小時，固定床內的流體部分處于過渡狀態，此時采用湍流模型來計算壓降誤差較大；而隨著Rep的增大，流體逐漸處于湍流狀態，此時采用湍流模型模擬壓降所得結果與半經驗公式計算結果之間的誤差逐漸減小；但隨著流體速度的進一步增大，相對誤差繼續增大。

比較圖5和圖9也可以看出，隨著填充顆粒粒徑不均勻度的增大，在相同的Rep下，模擬結果與半經驗公式計算結果之間的相對誤差增大，造成這種現象的主要原因是：隨著填充顆粒不均勻度的增大，床層內部結構變得更加復雜，流體流過的通道變得更加扭曲，此時采用各向同性的standardk-ε模型湍流模型和原有的計算網格來計算床層壓降使相對誤差增大。

3　結論

采用CFD法研究小D/dp的固定床內的壓降，基于standardk-ε模型、SIMPLE算法、邊界層等方法和模型進行模擬計算，得到的結論主要有：

對于單一粒徑顆粒填充的固定床，在低雷諾數即Rep小于120左右時，CFD法和半經驗公式能夠預測到相似的壓降值，而在高雷諾數下二者之間的相對誤差有所增大，并呈現先減小后增大的趨勢

對于填充不同粒徑顆粒的固定床，選用d43粒徑作為有效粒徑，能夠更好解釋床層空隙率的分布形式。同時，采用d43替代原半經驗公式的粒徑參數得到的壓降值與模擬結果最為接近，對于小D/dp固定床選用d43作為有效直徑能夠提高半經驗公式的預測準確度。

參考文獻：

[1]Reichelt W. Zur Berechnung des Druchverlustes einphasig durchstr?mter kugelund Zylinderschüttugen[J]. Chem Ing Tech, 1972, 23: 342-361

[2]Eisfeld B, Schnitzlein K. The influence of confining walls on the pressure drop in packed beds[J]. Chemical Engineering Science, 2001, 56: 4 321-4 329

[3]Ergun S. Fluid flow through packed columns[J]. Chem Eng Prog, 1952, 48(2): 89-94

[4]Carman P C. Fluid flow through granular beds[J]. Transactions of the Institution of Chemical Engineers, 1937, 15: 150-166

[5]Zeisberger A, Mayinger F. Heat transport and void fraction in granulated debris[J]. Nuclear Engineering and Design, 2006, 236: 2 117-2 123

[6]Li L, Ma W. Experimental characterrization of the effective particle diameter of a particulate bed packed with multi-diameter spheres[J]. Nuclear Engineering and Design, 2011, 241: 1 736-1 745

[7]Li L, Ma W. Experimental study on the effective particle diameter of a packed bed with non-spherical particles[J]. Transp Porous Med, 2011, 89: 35-48

[8]Dalman M T, Merkin J H, Mcgreavy C. Fluid flow and heat transfer past two spheres in a cylindrical tube[J]. Computers & Fluids, 1986, 14: 267-281

[9]Calis H P A, Nijenhuis J, Paikert B C,etal. CFD modeling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing[J]. Chemical Engineering Science, 2001, 56: 1 713-1 720

[10]Reddy R K, Joshi J B. CFD modeling of pressure drop and drag coefficient in fixed and expended beds[J]. Chemical Engineering Research and Design, 2008, 86: 444-453

[11]Atmakidis T, Kenig E Y. CFD-Based analysis of the wall effect on the pressure in packed beds with moderate tube/particle diameter ratios in the laminar flow regime[J]. Chemical Engineering Journal, 2009, 155: 404-410

[12]Maker M J, Tabor G R. Computational analysis of transitional air flow through packed columns of spheres using the finite volume technique[J]. Computers and Chemical Engineering, 2010, 34: 878-885

[13]Reddy R K, Joshi J B. CFD modeling of pressure drop and drag coefficient in fixed beds: Wall effects[J]. Particuology, 2010, 8: 37-43

[14]Eppinger T, Seidler K, Kraume M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios[J]. Chemical Engineering Journal, 2011, 166: 324-331

[15]Augier F, Idoux F, Delenne J Y. Numerical simulations of transfer and transport properties inside packed beds of spherical particles[J]. Chemical Engineering Science, 2010, 65, 1 055-1 064

[16]Theuerkauf J, Witt P, Schwesig D. Analysis of particle porosity distribution in fixed beds using the discrete element method[J]. Powder Technology, 2006, 165: 92-99

[17]DeKlerk A. Voidage variation in packed beds at small column to particle diameter ratio[J]. AIChE J, 2003, 49: 2 022-2 029

[18]DuToit C G. The numerical determination of the variation in the porosity of the pebble-bed core[J]. In: Proceedings of 1stinternational topical meeting on high temperature reactor technology (HTR2002), 2002, Petten, Netherlands

[19]Guardo A, Coussirat M, Larrayoz M A,etal. Influence of the turbulence model in CFD modeling of wall-to-fluid heat transfer in packed beds[J]. Chemical Engineering Science, 2005, 60: 1 733-1 742