用相對運(yùn)動方法解兩道競賽試題
馬廣明 浦仕畢
·競賽園地·
用相對運(yùn)動方法解兩道競賽試題
馬廣明 浦仕畢
(北京市第十二中學(xué),北京 100071)
相對運(yùn)動觀點(diǎn)是分析運(yùn)動問題的一種重要思想方法,尤其是在分析處理運(yùn)動學(xué)中的兩個物體同時發(fā)生運(yùn)動的相關(guān)問題時十分必要且有效.本文對物理競賽試題中的兩道運(yùn)動問題用相對運(yùn)動方法進(jìn)行實(shí)例分析,以凸顯此種方法的精妙.
相對運(yùn)動;相對速度;矢量關(guān)系
第33屆全國中學(xué)生物理競賽預(yù)賽試題,有兩道涉及同一平面上兩物體的直線運(yùn)動內(nèi)容.這兩個問題,若運(yùn)用相對運(yùn)動觀點(diǎn)處理,解法簡單、直觀.
題1.從樓頂邊緣以大小為v0的初速度豎直上拋一小球;經(jīng)過t0時間后在樓頂邊緣從靜止開始釋放另一小球.若要求兩小球同時落地,忽略空氣阻力,則v0的取值范圍和拋出點(diǎn)的高度

解析:兩個小球都在豎直方向上發(fā)生運(yùn)動時,在其中一個球上觀察另一個球,其做勻速直線運(yùn)動.
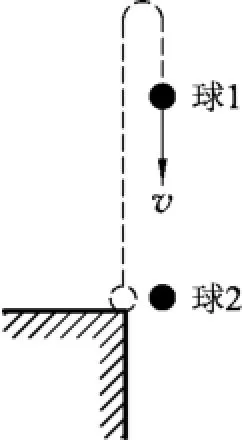
圖1
設(shè)球1某時刻開始做豎直上拋運(yùn)動,球2經(jīng)過時間t0開始做自由落體運(yùn)動.要求兩小球同時落地,就是在t0時刻,在球2上觀察球1,看到球在其上方距離球2一定距離h處,并向下以一定速度向球2運(yùn)動.如圖1所示.
t0時刻球2的速度為0,球1此時的速度v1=v0-gt0就是球1相對球2做勻速運(yùn)動的速度.兩個要求:①v1方向豎直向下;②v1的大小小于v0.否則球1回到了拋出點(diǎn)或以下,先于球2落地.由此得出<v0<gt0.
滿足上述速度要求的條件下,t0時刻球1位于球2上方,且以速度v1勻速向球2運(yùn)動,經(jīng)歷時間t=H/v1球1追上球2,兩球相遇.則拋出點(diǎn)距地面的高度也就是對應(yīng)時間內(nèi)球2自由落體運(yùn)動下落的高度為
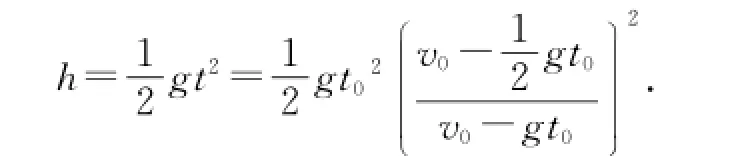
此題選項(xiàng)(C)正確.
題2.一足球運(yùn)動員1自A點(diǎn)向球門的B點(diǎn)踢球,已知A、B之間的距離為s,球自A向B的運(yùn)動可視為水平地面上的勻速直線運(yùn)動,速率為u,另一足球運(yùn)動員2到AB連線的距離為l,到A、B兩點(diǎn)的距離相等.運(yùn)動員1踢出球后,運(yùn)動員2以勻速v沿直線去攔截該球.設(shè)運(yùn)動員2開始出發(fā)去攔截球的時刻與球被運(yùn)動員1踢出的時刻相同.
(1)如果運(yùn)動員2能攔截到球,求運(yùn)動員2開始出發(fā)去攔截球直至攔截到球的時間間隔,球被攔截時球到A點(diǎn)的距離、球到運(yùn)動員2出發(fā)點(diǎn)的距離和運(yùn)動員2運(yùn)動的方向與A、B連線的夾角.
(2)為了使運(yùn)動員2能攔截到球,求u、v、s和l應(yīng)當(dāng)滿足的條件.
參考解答給出的解法是:記運(yùn)動員1踢出球的時刻為零時刻.設(shè)運(yùn)動員2沿著與A、B連線夾角為θ的方向運(yùn)動,球在時刻t被運(yùn)動員2攔截.令球被攔截時球到A點(diǎn)和運(yùn)動員2到出發(fā)點(diǎn)的距離分別為s1和s2,則

由幾何關(guān)系有

從(3)、(4)消去θ,并利用(1)、(2)式得
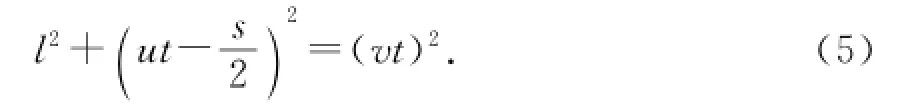
此即

這是關(guān)于t的一元二次方程,解為
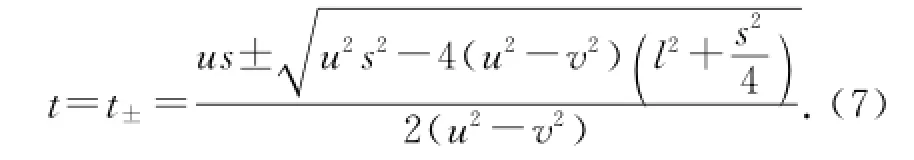
由(1)、(2)、(7)式得
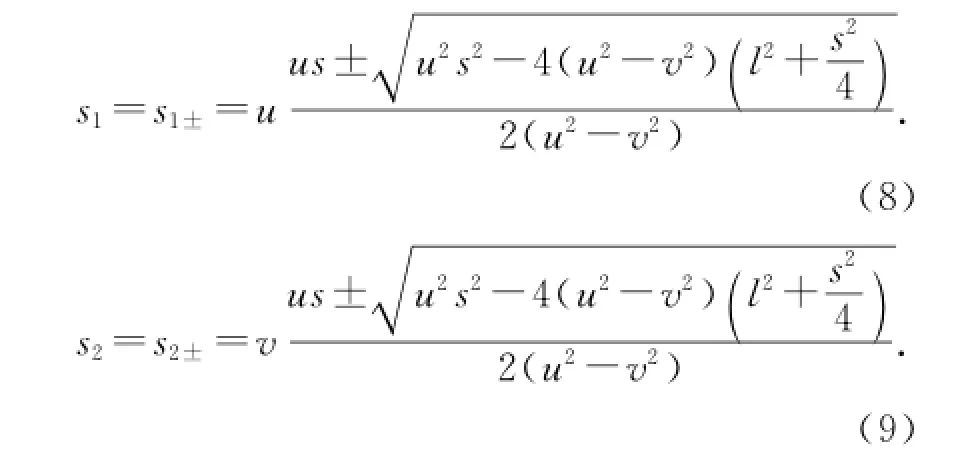
由(4)、(9)式得
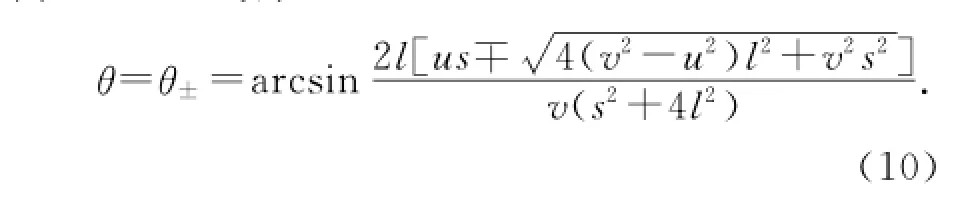
(2)方程(6)有實(shí)數(shù)解的條件是
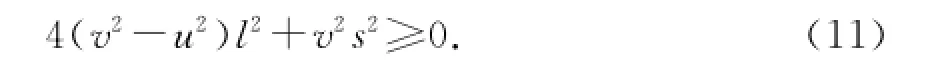
依題意有t>0的條件要求,則

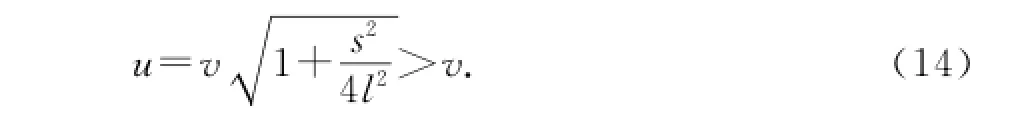
(7)~(10)式則為


運(yùn)動員2只能在一處攔截到球.
本文給出運(yùn)用相對運(yùn)動觀點(diǎn)的分析如下.
由題設(shè),開始時,球與運(yùn)動員2的位置之間幾何關(guān)系如圖2所示:圖中AB與AC間夾角為α,其中AC間的距離為運(yùn)動員2與1相遇,就是在運(yùn)動員2看來,球于距離為的A處向自己勻速運(yùn)動過來.其速度矢量圖如圖3所示,滿足:
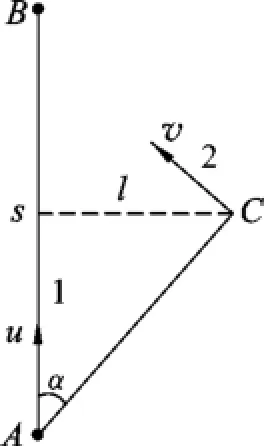
圖2
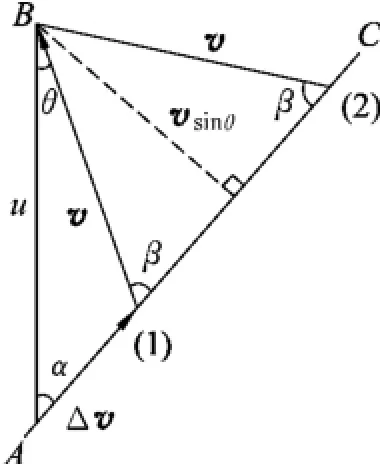
圖3

從分解的角度來認(rèn)識相應(yīng)關(guān)系.
(1)在垂直AC線方向上,兩運(yùn)動員的分速度相等,則

(2)在平行于AC線方向上,ucosα,vcosβ構(gòu)成了兩者的相對運(yùn)動速度,但存在圖3中標(biāo)注的(2)和(1)兩種情況.
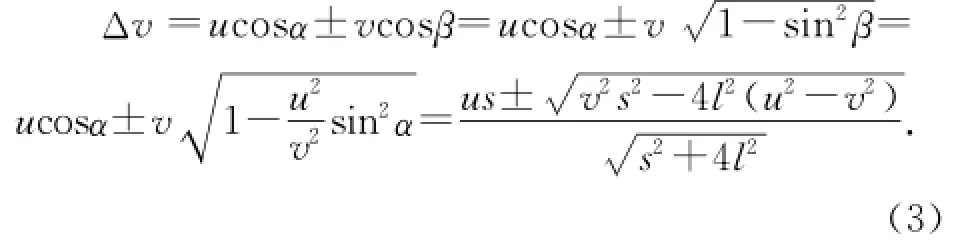
① 計(jì)算.相遇時間間隔,球運(yùn)動的路程,運(yùn)動員2運(yùn)動的路程分別為
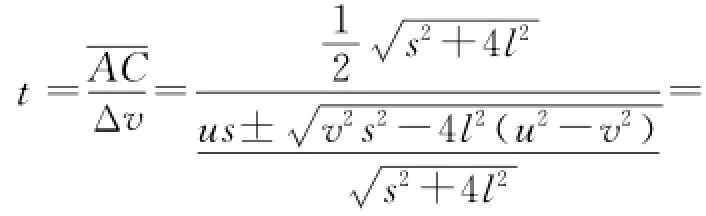

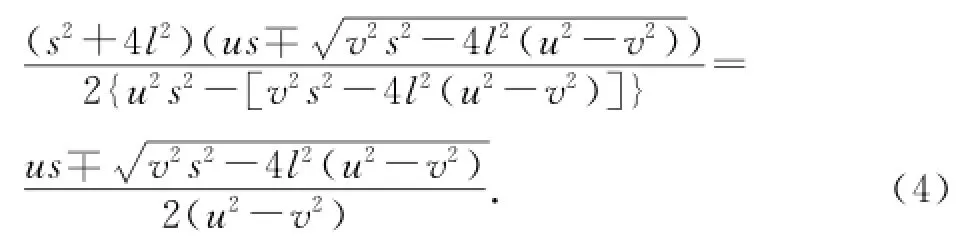
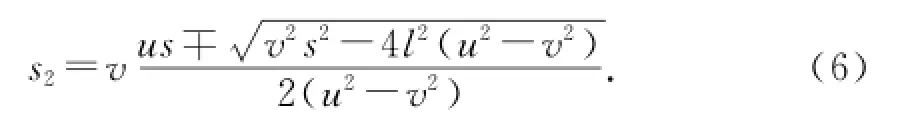
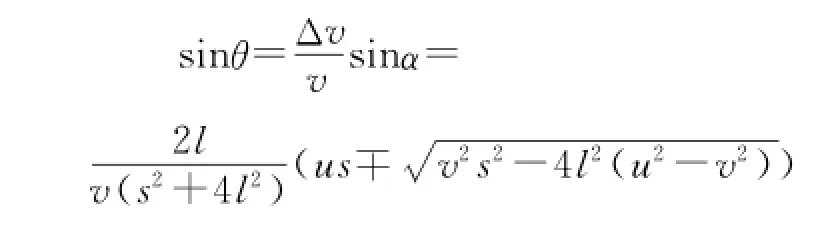
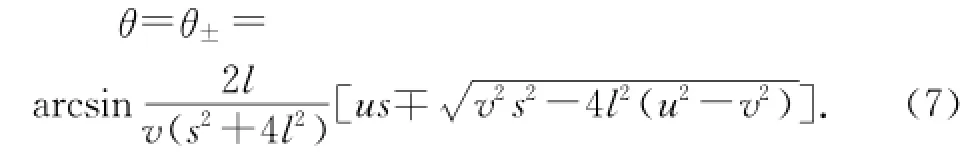
② 攔截條件的分析.
若矢量三角形存在,v有最小值vmin,圖3所示.則v≥usinα,代入sinα值,所求條件為
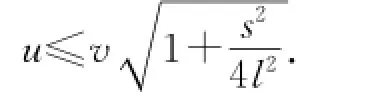
需要特別說明的是,參考答案給出的解法中關(guān)于u的數(shù)值關(guān)系的(14)式,即,是不全面、不準(zhǔn)確的,其正確關(guān)系表示應(yīng)如上式所示.
由上比較可見,用相對運(yùn)動方法分析層次分明,物理意義明顯,對問題理解有特殊功效,不可忽視.
2016-09-16)

