基于透視投影的垂直視角投影算法研究

張建偉， 雷 霖

(成都大學 信息科學與工程學院， 四川 成都 610106)

基于透視投影的垂直視角投影算法研究

張建偉， 雷 霖

(成都大學 信息科學與工程學院， 四川 成都 610106)

在計算機視覺領域，透視投影變換是圖像變換中最復雜的變換之一.在透視投影中的垂直投影是在實際工程應用中使用最廣泛的變換方法.研究了透視變換中斜投影與正投影之間的變換關系，分析了不同角度的斜投影圖像到正投影圖像之間變換對參數(shù)的影響，得出了變化參數(shù)與斜投影的傾角關系.實驗表明，按照所得到的參數(shù)與傾角關系矩陣，可以準確地計算出斜投影圖像對應的正投影圖像.

垂直投影；透視變換；圖像投影；圖像處理

0 引 言

圖像處理領域中，投影技術是實現(xiàn)三維立體信息到二維平面信息的主要手段.目前，圖像幾何中，主要有2類投影技術：一是平行投影；二是透視投影.其中，透視投影是攝像機捕獲圖像信息的幾何模型，應用更為廣泛.在實際應用中，由于實際環(huán)境的限制，攝像機并不能捕獲垂直視角的圖像(即正投影圖像)，而視角傾斜得到的斜投影圖像有一個很大的缺陷就是不直觀，尤其是距離和三維空間位置的感知，使得人眼無法預測距離的遠近.對此需要對攝像機獲取的斜投影圖像進行二次投影變換得到垂直視角投影圖像，以便得到更直觀的視覺信息和三維信息.隨著圖像處理技術的快速發(fā)展，對透視投影技術的研究也逐漸深入[1-3].但目前對垂直視角投影與斜投影之間參數(shù)關系的研究相對較少，特別是垂直視角變換中角度、距離與變換參數(shù)之間的關系.基于此，本研究對斜投影到垂直視角投影的變換參數(shù)矩陣進行了深入分析，將各個參數(shù)之間的關系及影響因素做了詳細探討，并進行了仿真實驗.

1 透視投影變換

在圖像處理中，圖像變換是最基本的處理方法之一，包括簡單變換與復雜變換.簡單變換包括，改變圖像位置的平移變換、改變圖像大小的尺度變換以及改變圖像角度的旋轉變換等；復雜變換則有，三維到二維的透視變換、用于直線檢測的霍夫變換等.

透視投影變換是圖像變換中最復雜的變換之一.從幾何學角度來說，平移、旋轉、尺度變換、相似變換、仿射變換都只是透視變換的一種特殊形式.因此，介紹透視投影之前，需要先對其他幾種變換的原理進行了解和分析，其他各變換的公式[4-6]如下，

(1)

(2)

(3)

(4)

(5)

(6)

其中，式(1)是平移變換，式(2)是旋轉變換，式(3)是尺度變換，式(4)是相似變換，式(5)是仿射變換，式(6)是透視變換；x、y為變換前坐標，x′、y′為變換后坐標.關于各個參數(shù)的具體含義可以在文獻[6]中查閱.

從以上一系列公式中看出，變換的參數(shù)從旋轉與尺度變換的單參數(shù)到仿射變換的6參數(shù)再到透視變換的8參數(shù)，復雜度越來越高，而透視變換是其中計算最復雜的變換，其他變換都可以看成是透視變換的特殊形式.本研究重點分析相似變換、仿射變換和透視變換3個公式，其矩陣都是3×2矩陣，但相似變換只有4個參數(shù)，而仿射變換有6個參數(shù)，換句話說，相似變換是仿射變換的一種特殊形式.而透視變換有8個參數(shù)，因此仿射變換是透視變換矩陣的a31和a32為0時得到的矩陣.通常，在實際應用中，應遵從簡單原則，相似變換能解決的問題不使用仿射變換，仿射變換能解決的問題不使用透視變換[7].但由于實際工程的復雜性，很多問題需要透視變換解決，因此，對透視變換的研究等同于對以上所有變換的研究，這具有十分重要的意義.

透視變換的原理示意圖如圖1所示.

圖1 透視變換示意圖

從圖1可以看出，透視變換是將遠端的立體圖像投影到近平面圖像的過程，也是從三維到二維的過程，這也是攝像機的基本原理：對于景物目標中任何一個平面最終投影到攝像機的傳感器平面都遵守透視變換公式(6).

2 基于透視變換的垂直視角變換

2.1 透視投影變換矩陣求解

從攝像機直接采集到的圖像本身已經是外界三維圖像，按照透視變換公式(6)生成二維圖像，但由于位置關系，所采集的視角并不直觀(見圖1).圖像中只有部分平面是正投影，其他底平面、頂平面、左平面及右平面都是斜投影.從幾何理論可知，垂直視角對于人的眼睛是最直觀的接收視角(見圖2)，1號攝像機是斜視角，2號攝像機是垂直視角.在監(jiān)控行業(yè)，很多攝像機不能安裝為垂直視角，尤其是室外的監(jiān)控，這對很多視頻的智能分析尤其是周界報警算法的實現(xiàn)是非常不利的.對此，利用透視變換的原理和攝像機與近平面的夾角之間的關系，可以將斜投影進行二次投影為垂直變換.

圖2 斜投影和垂直視角投影示意圖

為了能夠更準確描述透視投影和攝像機與拍攝平面之間的關系，本研究利用一張標準的圖形作為標定圖(見圖3(a))，標定圖由5×6共30個正方形的格子構成，然后通過調整攝像機的角度拍攝出不同傾斜角度的斜投影圖像(見圖3(b)).

圖3 透視投影標定圖與斜視投影圖像

按照透視變換原理，若要將斜投影圖像變?yōu)榇怪币暯峭队埃恍枰业阶儞Q前和變換后圖像4個點對坐標(u1，v1)(u2，v2)(u3，v3)(u4，v4)，映射后為(x1′，y1′)(x2′，y2′)(x3′，y3′)(x4′，y4′)，即可聯(lián)立方程求解出透視變換矩陣，其中4個點中任意3點不能在同一直線上.式(6)透視變換的完整形式為，

(7)

將式(7)變換為等式形式，

(8)

將4對點代入式(8)，得到8個方程，聯(lián)立可得8個參數(shù)，最后獲得變換矩陣，其中a33=1.

2.2 透視投影矩陣與斜視投影夾角關系

為了更方便地分析斜視投影與垂直視角投影夾角與變換矩陣參數(shù)的關系，在標定圖中設定固定的對應點對，如圖4中的黑色圓點.接著，通過改變斜視投影面與垂直投影面的夾角獲取不同的投影圖，并通過對應點解算透視變換矩陣得到垂直視角的圖像，得到矩陣參數(shù)與夾角數(shù)據(jù)的參數(shù)表，最后根據(jù)參數(shù)表來確定參數(shù)與角度變換的關系.

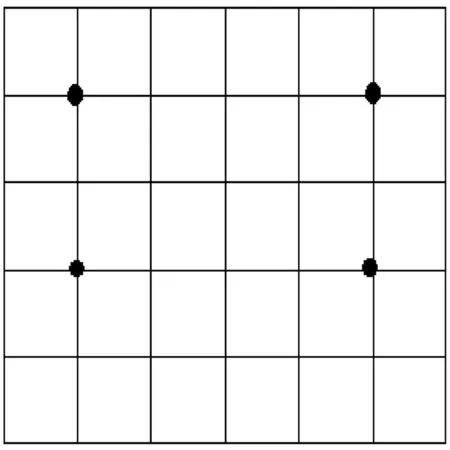
圖4 標定圖中選定的標定點

為確認參數(shù)的初始值，先對圖3(b)做正投影變換，得到以下參數(shù)：

a11=0.553240974820510；

a12=1.28142380422692；

a13=-23.6818687430476；

a21=1.60617858226312；

a22=0；a23=-188.793103448276；

a31=0.00116290828192943；

a32=0；a33=1

該參數(shù)矩陣所完成的變換實際上就是從一個等腰梯形的四邊形變換為一個矩形.其中，a12和a32為0；a22控制旋轉變化，由于本次變換圖像并未發(fā)生旋轉，因此為0；a32控制x方向的透視變換，在本次變換中主要是y方向的，因此為0.當不為0時，投影效果如圖5(b)和5(c)所示，其中5(a)為正投影的情況.由于實際拍攝的環(huán)境不是理想情況，打印方格的紙張存在一定的不平整，導致正投影最上面一條直線存在少量的彎曲.

圖5 a22和a32為0和不為0的變換對比

以上面的參數(shù)為基礎，就可以通過改變其他參數(shù)來找出矩陣中參數(shù)和斜投影的夾角之間的關系.

3 仿真實驗

在仿真實驗中，采用圖3(a)作為標定圖，分別在40 °、50 °、60 °和70 °斜視投影下進行圖像采集(見圖6).根據(jù)以上分析可知，在透視變換參數(shù)矩陣中，各個參數(shù)對于圖像的變換起著不同的作用，a31和a32是透視參數(shù)，其他參數(shù)都是仿射參數(shù)，也就是說其他參數(shù)不會產生透視，由于a32為0，因此此處主要考慮a31.在實驗中，只改變a31，將出現(xiàn)圖6中圖像的傾斜，因此還要考慮x方向的平移量，也就是a13.通過改變a31和a13來實現(xiàn)各種角度的正投影，如圖7和圖8所示.各個投影的實現(xiàn)所用的參數(shù)如表1所示.

圖6 單獨改變a31造成的圖像傾斜

圖7 各個角度的斜視投影圖

從表1看出，a31的值隨著角度增大相應變大，而a13則起調節(jié)作用，保證整個圖像在x方向是中心對稱且不出現(xiàn)傾斜.因此，在實際工程中可以通過a31和a132個變量來對各種傾角的斜投影進行正投影變換.

圖8 正投影變換后的垂直視角投影

相機傳感器傾角a11a12a1340°0．55321．2814-23．681850°0．55321．2814-113．681860°0．55321．2814-183．681870°0．55321．2814-223．6818相機傳感器傾角a21a22a2340°1．60620-188．793150°1．60620-188．793160°1．60620-188．793170°1．60620-188．7931相機傳感器傾角a31a32a3340°0．00120150°0．00140160°0．00160170°0．001801

4 結 論

透視變換是圖像處理算法中三維和二維轉換的關鍵技術，透視變換中的垂直視角變換是其在工程應用中最為廣泛的一種.本研究通過對透視參數(shù)矩陣的分析和實際斜投影圖像的仿真實驗表明，修改矩陣中的a31和a132個參數(shù)，而不需要對其他6個參數(shù)進行調整，即可以實現(xiàn)不同傾角的斜投影圖像到正投影圖像的變換，這在具體的圖像工程中具有實際意義.

[1]金勇俊，李言俊，張科.一種透視變換圖像金字塔匹配改進算法[J].計算機工程與應用，2007,43(24):78-80.

[2]劉洪濤，蔣如意，胡文，等.基于路面垂直輪廓建模的一般路面逆透視變換[J].上海交通大學學報，2012，56(11):1770-1773.

[3]楊彬，李旭東，晏磊，等.航空遙感圖像拼接算法及其精度評價[J].計算機工程，2014,40(3):253-257.

[4]姚敏．數(shù)字圖像處理[M]．北京：機械工業(yè)出版社，2012.

[5]陳自強.透視投影研究[J].華東理工大學學報,2000,26(2):201-205.

[6]Richard Hartley,Andrew Zisseerman．計算機視覺中的多視圖幾何[M]．韋穗，楊尚駿，章權兵，等譯.合肥：安徽大學出版社，2002．

[7]Lin W Y,Liu S Y,Matsushita Y,et al.Smoothlyvaryingaffinestitching[C]//IEEEConferenceonComputerVisionandPatternRecognition(CVPR2011).Colorado,USA:IEEE Press,2011:345-352.

Top-view Projection Algorithm Research Based on Perspective Projection

ZHANGJianwei,LEILin

(School of Information Science and Engineering, Chengdu University, Chengdu 610106, China)

In computer vision,perspective projection is one of the most complicated image transformations.The top-view projection in the perspective projection is applied widely in many engineering fields.In this paper,the correlation between top-view projection and tilt-view projection is studied,and the influence of the transformation from the tilt-view projections at different angles to top-view projections on the transformation parameters is analyzed.Therefore,the correlation between parameters and the tilt-angle is confirmed.Experiments show that based on the matrix relation between parameters and the angle of tilt,the expected top-view projection image that corresponds to the tilt-view projection can be obtained by accurate calculation.

top-view projection;perspective transformation;image projection;image processing

1004-5422(2017)01-0047-04

2016-10-12.

四川省科技廳科技支撐計劃(2015GZ0274)、 四川省教育廳理工類重點課題(15ZA0359)資助項目.

張建偉(1980 — )， 男， 博士， 副教授， 從事圖像處理與計算機視覺研究.

TP391.41

A