基于電離層殘差法的北斗周跳探測與修復研究
崔立魯, 溫孝居, 余 寒, 楊 磊, 宿 東
(成都大學 建筑與土木工程學院, 四川 成都 610106)
基于電離層殘差法的北斗周跳探測與修復研究
崔立魯, 溫孝居, 余 寒, 楊 磊, 宿 東
(成都大學 建筑與土木工程學院, 四川 成都 610106)
對北斗周跳探測與修復的問題,利用北斗衛星信號頻率特征以及電離層殘差法的基本原理,推導并構造了適用于北斗周跳探測與修復的周跳檢驗量,通過北斗實測數據和人為加入周跳的實驗方案,對該周跳檢驗量進行驗算.結果表明:電離層殘差法能夠較好探測和修復較小的周跳,適用于北斗周跳的探測與修復.
電離層殘差法;北斗系統; 周跳探測與修復
0 引 言
周跳的探測與修復是全球衛星導航系統(GlobalNavigationSatelliteSystem,GNSS)數據處理的必需步驟,常用方法有高次差法、M-W組合法、電離層殘差法及多項式擬合法等.隨著北斗衛星導航系統開始提供區域導航定位服務,越來越多的學者開始研究北斗周跳探測與修復的方法,例如,熊偉等[1]研究了偽距相位組合探測和修復周跳的數學模型,伍岳等[2]利用模擬數據研究了不同組合觀測值在周跳探測中的性能,黃令勇等[3]采用無幾何相位組合和偽距相位組合聯立方程組修復周跳,并克服了方程解的不穩定問題,劉俊等[4]探討了偽距相位組合法在不同類型衛星下的周跳探測性能.在相關研究基礎上[5-8],本研究根據北斗衛星的頻率特征和電離層殘差法的基本原理,推導并構造出適用于北斗周跳探測與修復的周跳檢驗量,并利用北斗觀測值文件設置相應的計算方案,驗證了該周跳檢驗量的準確性和可行性.
1 電離層殘差法
電離層殘差法用于周跳探測與修復,其主要是利用電離層殘差在各歷元間的變化判斷周跳的存在與否.這種方法有效地削弱了測量噪聲和多路徑效應,能有效地探測周跳.在同一歷元下,若不考慮多路徑效應和測量噪聲的影響,其雙頻載波相位值之差可以表示為,
(1)
將式(1)兩端同時除以λ1,則式(1)簡化為,
(2)
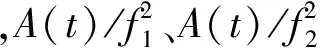
(3)
若ti到ti+1之間出現周跳ΔN即相鄰歷元間電離層殘差發生突變,設B1、B2載波上發生的周跳分別為ΔN1、ΔN2,則有,
(4)
由式(4)可以看出,ΔΦgf是ΔN1、ΔN2的線性組合,可以用n來表示.通過計算得到|ΔΦgf|,若|ΔΦgf|大于給定的閾值,則ti到ti+1之間發生了周跳,并且ΔN1、ΔN2即為B1、B2載波上的周跳數.
根據解算結果和最大3倍中誤差的標準,可以得到最大誤差為0.07周,即閾值為0.07周.根據式(4),得出表1~3.表中,ΔN1為相鄰歷元的L1載波相位觀測值之差(單位為周),ΔN2為相鄰歷元的L2載波相位觀測值之差(單位為周),ΔΦgf為殘差變化值(單位為周).
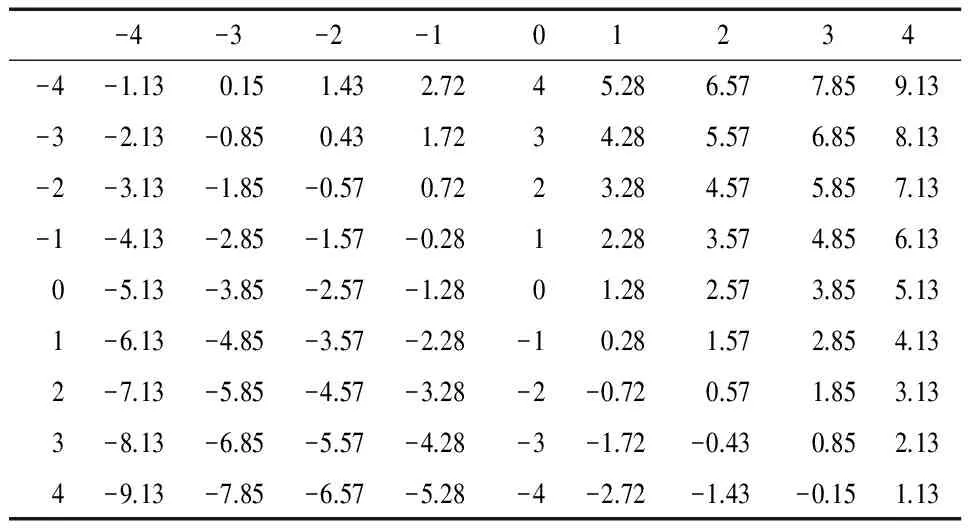
表1 ΔN1,ΔN2的組合ΔΦgf(ΔN1,ΔN2∈[-4,4])
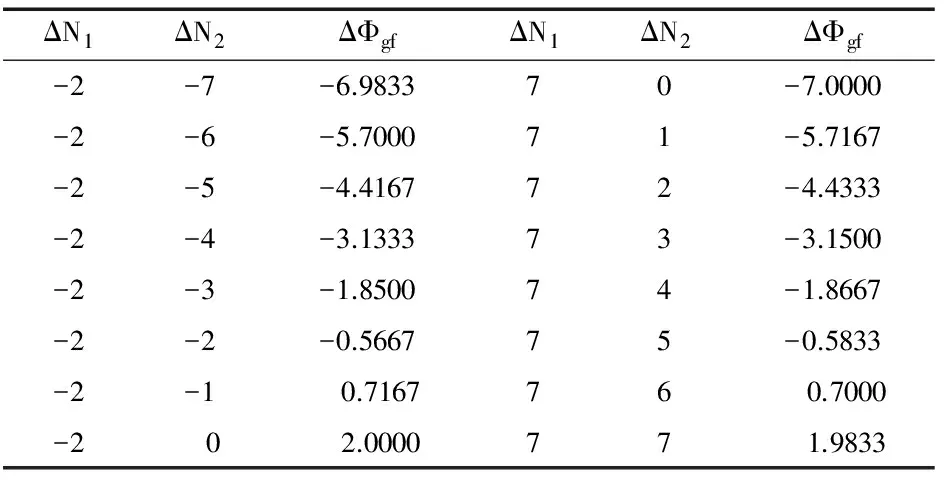
表2 ΔN1,ΔN2的組合ΔΦgf(ΔN1=-2,7;ΔN2∈[-7,7])
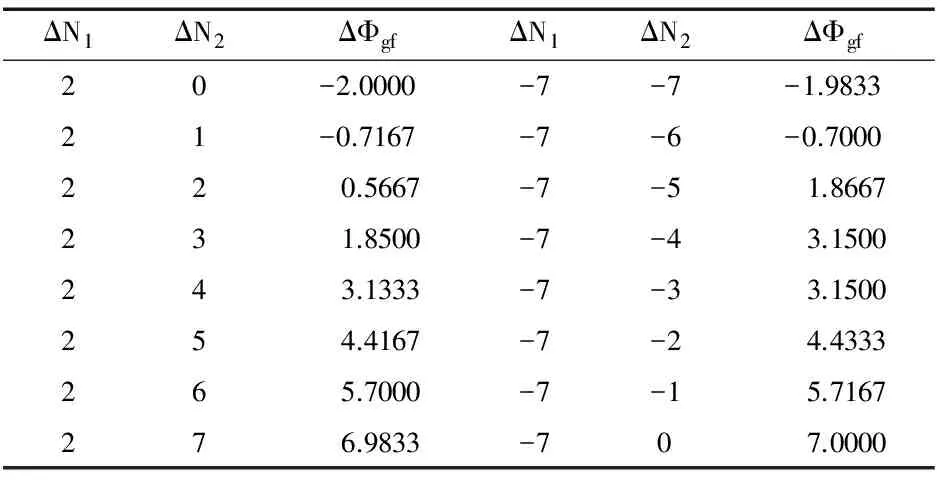
表3 ΔN1,ΔN2的組合ΔΦgf(ΔN1=2,-7;ΔN2∈[-7,7])
由表1~3可以看出,當不同的ΔN1與ΔN2組合在一起,得到的ΔΦgf差距有大有小,比如(2,0)和(-7,-7) 2個周跳組合得到的ΔΦgf差值只有0.02,也就是當求得ΔΦgf為-1.99左右時,根據式(4)將無法判斷是(2,0)和(-7,-7) 2個周跳組合中的哪個組合,這也表明了電離層殘差法存在多值性的問題.此外,從表2可以看出,當ΔΦgf在[-4,4]區間內的所有ΔΦgf值都大于0.12,因此不存在多值性問題,而且[-4,4]區域相當于小周跳來說足夠大.
2 數據計算和分析
2.1 數據來源和實驗設計
2.1.1 數據來源.
本研究的數據來源選用武漢大學衛星導航定位技術研究中心提供的北斗觀測值文件,選取的時間期間是2015年1月到2015年12月,數據采樣率為30s,采樣地點為武漢.為了更好地研究電離層殘差法對于周跳探測與修復的準確性和可行性.首先從觀測值數據中提出部分無周跳觀測值數據,然后再在此基礎上添加不同類型的周跳值.由于北斗衛星系統具有3種不同的衛星軌道,為了實驗數據的可比性,本研究采用的是傾斜地球同步軌道衛星(InclinedGeo-synchronizationOrbitSatellite,IGOS)的觀測值數據.
2.1.2 實驗設計.
本研究的數據計算實驗采用了如下3種方案:
方案1.在第10個歷元上添加(ΔN1,ΔN2)的周跳組合(3,0),即在第10個歷元的L1載波相位觀測值上加3.
方案2.在第20個歷元上添加(ΔN1,ΔN2)的周跳組合(0,-2),即在第20個歷元的L2載波相位觀測值上減2.
方案3.在第25個歷元上添加(ΔN1,ΔN2)的周跳組合(-4,1),即在第25個歷元的L1載波相位觀測值上減4,L2載波相位觀測值上加1.
2.2 數據比較和分析
數據計算結果如圖1~7及表4所示.
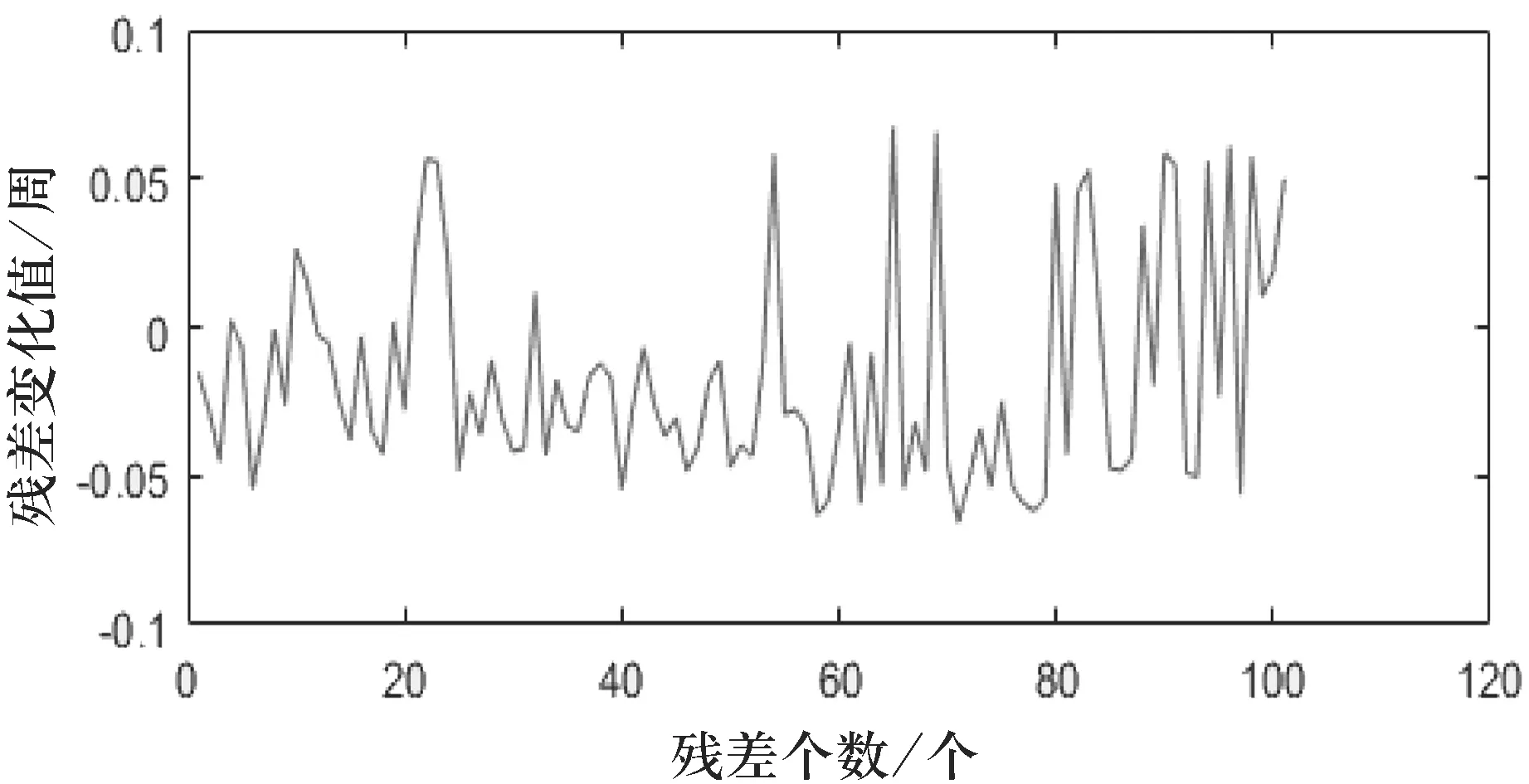
圖1 不含周跳的殘差變化值示意圖
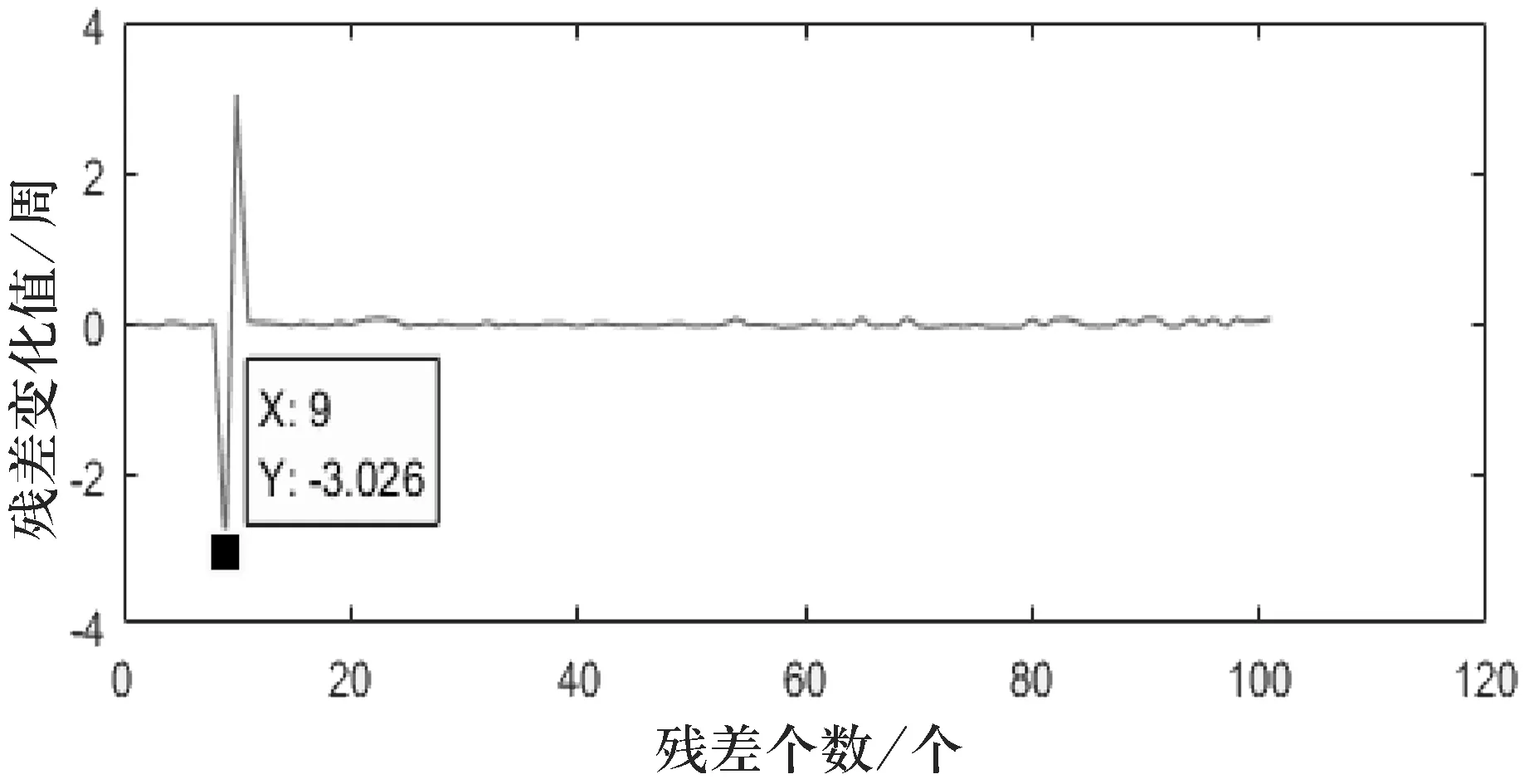
圖2 未修復的殘差變化值示意圖(方案1)
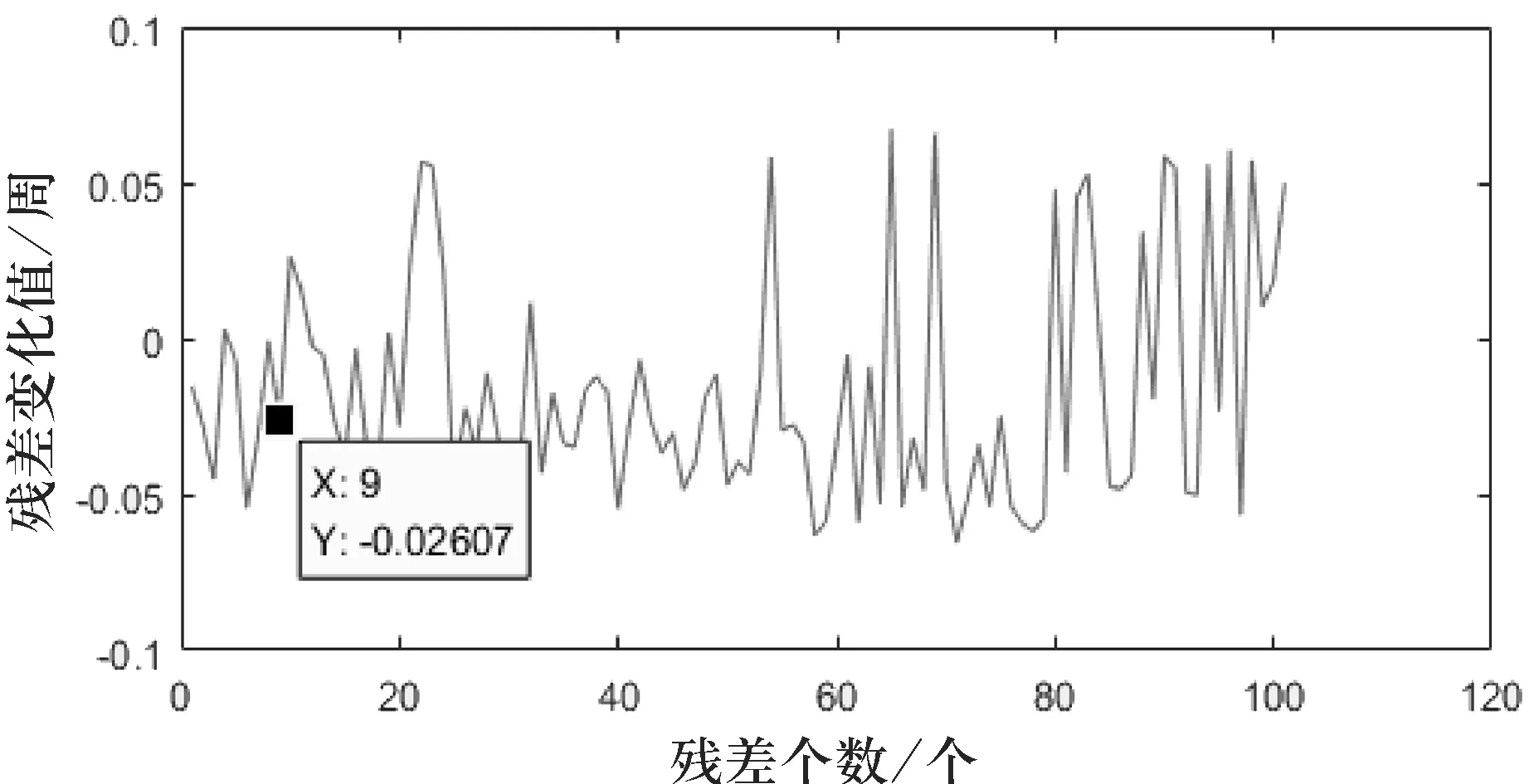
圖3 已修復的殘差變化值示意圖(方案1)
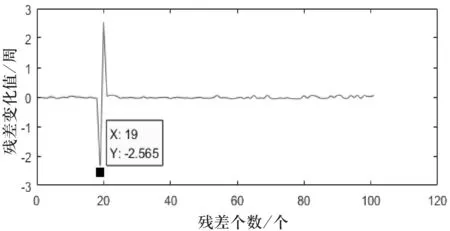
圖4 未修復的殘差變化值示意圖(方案2)

圖5 已修復的殘差變化值示意圖(方案2)
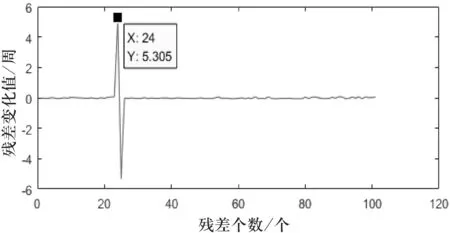
圖6 未修復的殘差變化值示意圖(方案3)
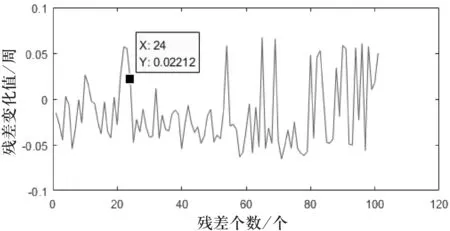
圖7 已修復的殘差變化值示意圖(方案3)
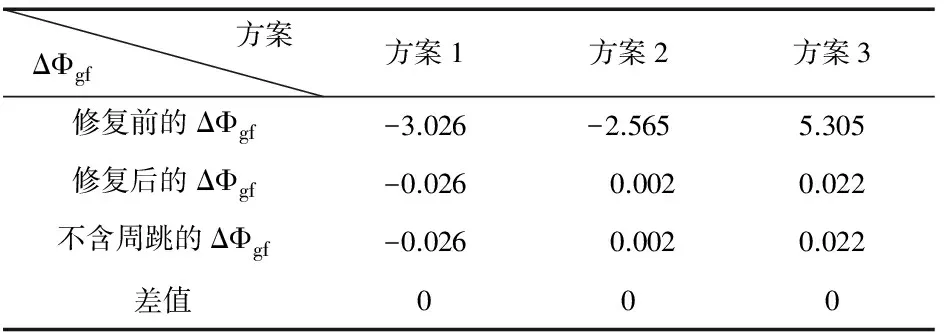
方案ΔΦgf 方案1方案2方案3修復前的ΔΦgf-3.026-2.5655.305修復后的ΔΦgf-0.026 0.0020.022不含周跳的ΔΦgf-0.026 0.0020.022差值000
*:ΔΦgf為殘差變化值(單位為周)
根據圖1~2、圖4、圖6可以看出,不含周跳的殘差變化值ΔΦgf均在[-0.07,0.07]內波動,而在加入周跳之后的殘差變化值ΔΦgf在加入周跳的歷元處出現較大的波動,其值大于閾值.
通過比較圖1、圖3、圖5、圖7可以看出,經過修復后的殘差變化值ΔΦgf與原數據的殘差變化值ΔΦgf一致,表示修復成功.
此外,從表4可以看出,不同的周跳組合所得的殘差變化值ΔΦgf均大于0.07,每個方案在經過修復之后殘差變化值ΔΦgf與未加入周跳前的ΔΦgf差值均為0,即完全無差異地修復了所加入的周跳.
結合以上圖和表數據可看出,電離層殘差法對于小周跳可以非常精確地進行探測并修復.
3 結 語
本研究利用北斗衛星信號頻率特點并結合電離層殘差法,構造了適用于北斗衛星系統的周跳檢驗量.為了更好地驗證該周跳檢驗量對于北斗周跳探測與修復的性能,設計了3個不同類型的方案,并進行了實測數據的計算.計算結果表明,利用該周跳檢驗量對北斗實測數據進行探測與修復后,能夠完全消除周跳對于觀測值的影響,尤其是對于小周跳的情況.本研究結果表明,電離層殘差法在北斗周跳探測與修復中同樣有著良好的應用前景.
需說明的是,本研究也存在一定不足,比如,周跳有大有小,還存在一些特殊周跳,因此,僅憑一種方法無法完全對周跳進行良好的修復.最好的方式是綜合采用多種方法進行處理.此外,本研究使用雙頻信號處理方法時,沒有考慮到北斗信號的三頻特性,這也是處理GPS信號和北斗衛星系統信號的區別,同時也是本課題下一步研究的重點方向.
[1]熊偉,伍岳,孫振冰,等.多頻數據組合在周跳探測和修復上的應用[J].武漢大學學報(信息科學版),2007,32(4):319-322.
[2]伍岳.第二代導航衛星系統多頻數據處理理論及應用[D].武漢:武漢大學,2005.
[3]黃令勇,宋力杰,王琰,等.北斗三頻無幾何相位組合周跳探測與修復[J].測繪學報,2012,41(5):763-768.
[4]劉俊,何秀鳳,劉炎雄.北斗三頻非差觀測數據的周跳探測與修復方法[J].大地測量與地球動力學,2014,34(4):117-122.
[5]崔立魯,朱貴發.利用重力衛星數據恢復地球質量遷移方法的研究[J].科學技術與工程,2015,14(15):106-109.
[6]崔立魯.重力衛星加速度數據的插值算法研究[J].測繪工程,2012,21(3):21-25.
[7]崔立魯.GPS衛星星歷仿真[J].成都大學學報(自然科學版),2015,34(3):307-310.
[8]陳洪武,胡斌,田鋮.北斗衛星導航系統在海洋工程中的應用[J].全球定位系統,2016,41(2):121-124.
Research on Detection and Restoration of Beidou Cycle Slip Based on Ionosphere Residual Method
CUILilu,WENXiaoju,YUHan,YANGLei,SUDong
(School of Architecture and Civil Engineering, Chengdu University, Chengdu 610106, China)
Aiming at the Beidou cycle slip detection and restoration,the paper,based on the Beidou signal frequency characteristics and the principle of the ionosphere residual method,derives and constructs the cycle slip detection observable that fits for Beidou cycle slip detection and restoration.Through the measured Beidou data and the experiment schemes with the cycle slip joined by people,the cycle slip detection observable is calculated.The conclusion shows that the ionosphere residual method can better detect and repair the smaller cycle slip,and it is suitable for Beidou cycle slip detection and restoration.
ionosphere residual method;Beidou;cycle slip detection and restoration
1004-5422(2017)01-0062-04
2016-11-30.
成都大學校青年基金(2014XJZ22)資助項目.
崔立魯(1983 — ), 男, 博士, 講師, 從事衛星導航系統定位技術研究.
P228.4
A

