一道貴州省模擬題的多種解法

云南省蒙自市蒙自一中(新校區)(661100)

蘇保明●

一道貴州省模擬題的多種解法

云南省蒙自市蒙自一中(新校區)(661100)

蘇保明●

隨著新課改的進一步實施與推進，選修內容越來越被命題者所親睞.選修4-5《不等式選講》是選考內容的重要內容，其中證明不等式問題又是高考考查的重點題型之一 .本文例舉一例研究不等式的證明方法，供參考.

(Ⅰ)求m的值；

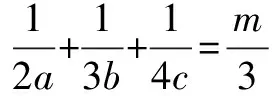
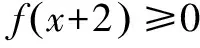
針對第(Ⅱ)問，經過筆者認真思考和研究，給出下面六種解法：

方法一、常數代入法

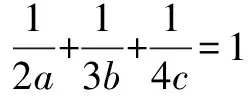
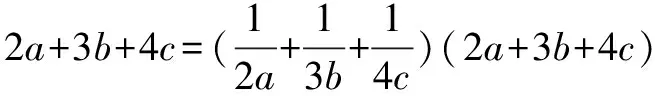
所以2a+3b+4c≥9.

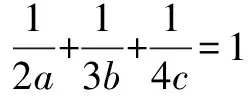
因為a>0,b>0,c>0，

所以2a+3b+4c≥9.

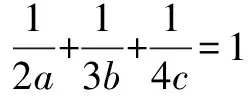
因為2a+3b+4c>0，所以2a+3b+4c≥9.

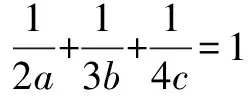
方法四：向量法

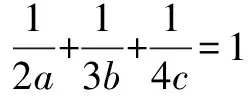
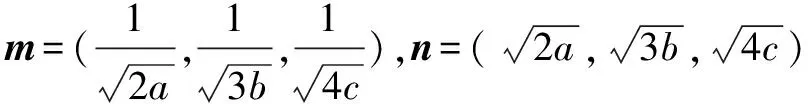
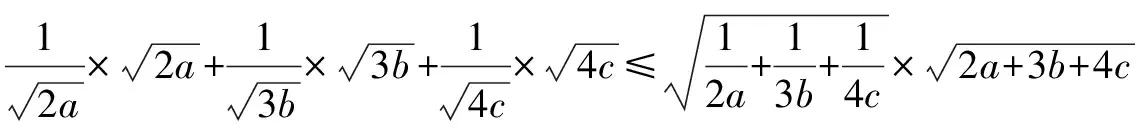
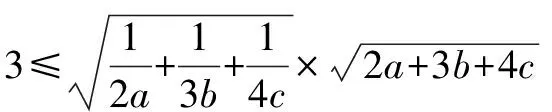
所以2a+3b+4c≥9.

方法五、柯西不等式法

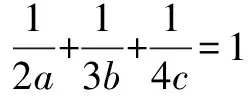
因為a>0,b>0,c>0，所以由柯西不等式，得

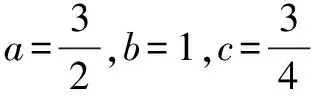
所以2a+3b+4c≥9.

評注 柯西不等式的引入，為解決某些相關的數學問題添增了新的思想方法，給解題者一種快樂感和成功感.此法通俗易懂，容易掌握，值得借鑒和學習.

方法六、利用方差的性質

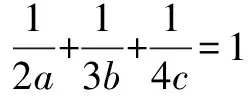
因為a>0,b>0,c>0，所以構造離散型隨機變量X的分布列：

X2a3b4cP12a13b14c

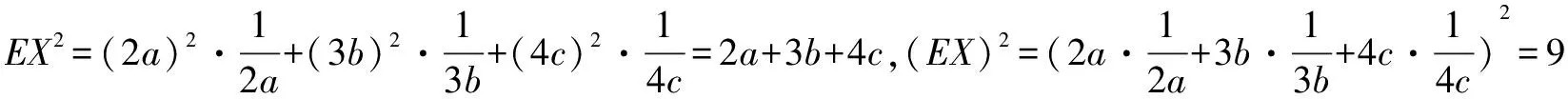
所以由方差的性質EX2≥(EX)2得2a+3b+4c≥9.

評注 用此法解決問題的關鍵就是能正確構造離散型隨機變量的分布列，而是否正確構造的關鍵又在于EX2≥(EX)2中是否出現所需要的式子2a+3b+4c.此法帶有很強的技巧性，必須熟練掌握才能運用自如.

G632

B

1008-0333(2017)07-0005-02