關注導數與其他知識的交匯

陜西省西安市臨潼區馬額中學(710609)

童永奇●

關注導數與其他知識的交匯

陜西省西安市臨潼區馬額中學(710609)

童永奇●

類型一、導數與“函數奇偶性”的交匯

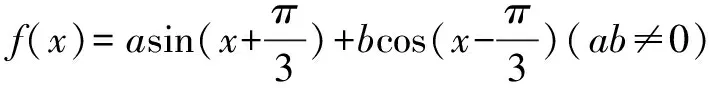
評注 為了實現函數奇偶性的相互轉化，靈活運用可導奇偶函數的導數特征性質：(1)可導奇函數的導數是偶函數；(2)可導偶函數的導數是奇函數.

類型二、導數與“三角函數最值”的交匯

例2 設當x=θ時，函數f(x)=sinx-2cosx取得最大值，則cosθ=____．

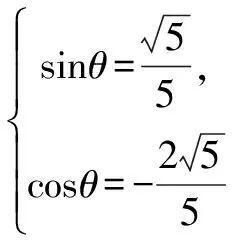
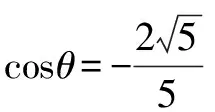
評注 一般地，設函數f(x)=asinx+bcosx(ab≠0)，則結合函數f(x)的圖象易知：若x=x0時函數f(x)取得最值，則函數f(x)在x=x0處的切線斜率為零，即f′(x0)=0.這個結論充分揭示了三角函數的最值與導數的緊密聯系.

類型三、導數與“函數零點”的交匯

A.0 B.1 C.2 D.3

解析 求導得f′(x)=1-x+x2-x3+…+x2016，可知：當x=-1時，f′(x)>0；

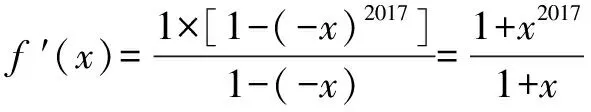
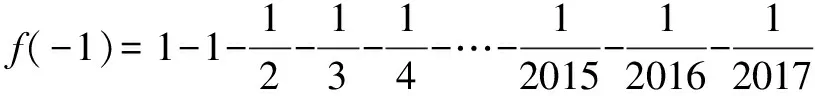
評注 本題具有一定的綜合性，對能力的考查較強，解題關鍵是靈活利用“分類與整合思想”準確分析導數與零的大小關系.

類型四、導數與“數列最值項”的交匯

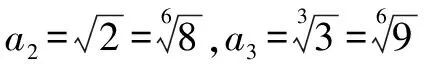
評注 當數列的通項公式所對應的函數的單調性復雜而較難判定時，需要借助導數來判定．本題中函數f(x)=x1/x的求導公式未知，只不過知道(xα)′=αxα-1(α為常數)，(ax)′=axlna(a>0且a≠1)，于是需要先對函數解析式做適當變形，再求導．

類型五、導數與“圓錐曲線最值問題”的交匯

解析 設點M(x,y)，則因為拋物線的準線為x=-1，所以結合拋物線的定義即得

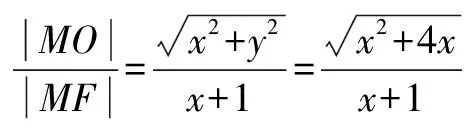
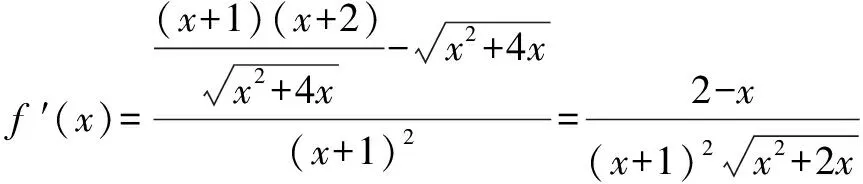
評注 本題設出動點M的坐標，有利于將目標問題等價轉化為求函數的最大值——可利用“導數法”(已給出)，還可利用“換元、配方法”

(提示：令t=x+1).

類型六、導數與“二項式求和問題”的交匯

例6(2016·天星預測卷)已知(2-x)100=a0+a1x+a2x2+…+a99x99+a100x100(x∈R)，則a1+22a2+32a3+…+992a99+1002a100=( ).

A.10000 B.-10000 C.9800 D.-9800

解析 設函數f(x)=(2-x)100，則f(x)=a0+a1x+a2x2+…+a99x99+a100x100，求導得f′(x)=a1+2a2x+3a3x2+…+99a99x98+100a100x99，

兩邊乘以x得xf′(x)=a1x+2a2x2+3a3x3+…+99a99x99+100a100x100，

兩邊求導得f′(x)+xf″(x)=a1+22a2x+32a3x2+…+992a99x98+1002a100x99.

又注意到f′(x)=-100(2-x)99，f″(x)=100×99×(2-x)98.

故取x=1，即得a1+22a2+32a3+…+992a99+1002a100=f′(1)+f″(1)=-100+100×99=9800.

評注 本題較難，對考生分析、解決問題的能力提出了較高的要求.解題關鍵：先構造函數，再充分利用“求導”思想及“賦值”技巧加以靈活處理.

類型七、導數與“不等式中比較大小”的交匯

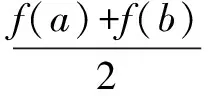
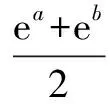
作差得：

構造函數g(a)=ea(b-a+2)+eb(b-a-2)，則g′(a)=ea(b-a+1)-eb.

因為g″(a)=ea(b-a)>0，所以函數g'(a)在R上單調遞增.

于是，由a

從而，由ag(b)=0，即ea(b-a+2)+eb(b-a-2)>0.

評注 上述求解的關鍵是將b看作“常量”，靈活地構造以a為變量的函數，充分利用函數的單調性比較大小.

綜上，關注導數與其他知識的交匯，有利于從導數角度看透問題的本質，進一步加深理解與認識，且學且悟！

G632

B

1008-0333(2017)07-0009-02