二項分布與超幾何分布的數學期望研究

北京101中學(100091)

方雯琪●

二項分布與超幾何分布的數學期望研究

北京101中學(100091)

方雯琪●

二項分布、超幾何分布是比較重要離散型分布，而它們之間不僅有聯系，還有存在區別，二項分布與超幾何分布的數學期望是反映隨機變量的一種非常重要的數字特征.因此，作為學生，我們應熟練掌握二項分布數學期望以及超幾何分布數學期望，并將之應用到實際生活中.本文就二項分布與超幾何分布的數學期望進行研究.

二項分布;超幾何分布；數學期望

在高中數學中，二項分布和超幾何分布是兩個非常重要的概率模型，這兩個概率模型能夠解決生活中的許多問題.在離散型隨機變量分布中，二項分布、超幾何分布是比較重要的分布，二項分布與超幾何分布兩者之間既存在聯系又有所區別.隨機變量的數學期望在概率論中占有非常重要的地位，它是反映隨機變量的數字特征.因此，對于學習高中數學來說，熟練掌握二項分布、超幾何分布的數學期望具有重要的意義.

一、二項分布與超幾何分布

1.二項分布

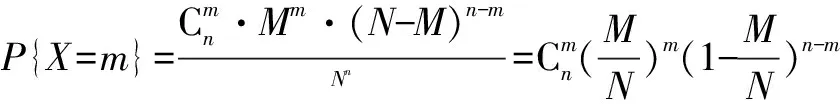
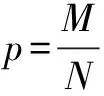
隨機變量X記為X～B(n，p)，X服從二項分布，即在n為1時，X服從0～1的分布.

2.超幾何分布

設某個產品有N件，在這些產品中正品有M件，采取不放回抽樣的方式從中抽取n件產品，用Y來表示抽取的產品中正品的個數，則有m件正品的概率為：

隨機變量Y記為Y～H(n，M，N)，Y服從超幾何分布

3.二項分布與超幾何分布的關系

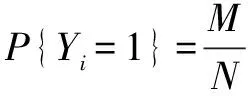
超幾何分布的極限分布是二項分布，即

二、二項分布與超幾何分布的數學期望

1.二項分布的數學期望

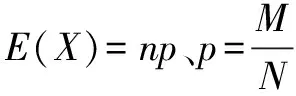
(1)定義法求解：

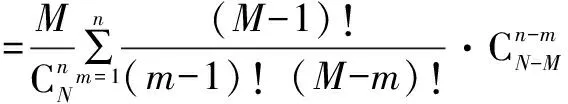
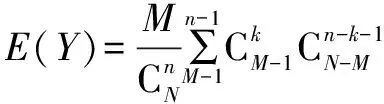
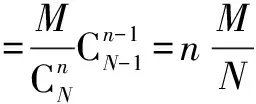
(2)利用性質求解：

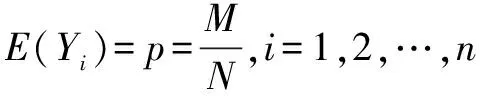
2.超幾何分布的數學期望

與二項分布的數學期望相比，超幾何分布的數學期望也可以應用定義法和利用性質進行求解，但是定義法求解的數學期望比利用性質求解的數學期望更麻煩，然而超幾何分布的數學期望與二項分布的數學期望相同.值得一提的是，隨機變量和的數學期望與隨機變量數學期望的和相等，但是這些隨機變量并不一定是相互獨立的.

例1 某種產品有80件，在這些產品中次品有8件，采取抽樣的方式從中抽取4件產品，計算出在這4件產品中次品數的期望值.

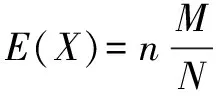
例2 一送客車載了20位乘客，從起點到終點之間有10個車站可以供乘客下車，但只有乘客下車才會在站點停車，乘客不下車就不停車.用X表示停車的次數，求E(X).

解Xi為第i站有人下車，i=1，2，…，10,X=X1+X2+…+X10，則E(X)值為多少.

乘客在第i站不下車的概率為(9/10)，那么這20位乘客在第i站不下車的概率為(9/10)20，則乘客在第i站下車的概率為1-(9/10)20.

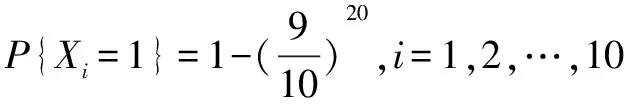
E(X)=E(X1+X2+…+X10)=E(X1)+E(x2)+…+E(X10)=10[1-(9/10)20]=8.8.

上述的求解方法是先將X分解，再利用隨機變量和的數學期望與隨機變量數學期望之和是相等的來求解，這種方法具有一定的實際意義且在某種程度上可以簡化問題.

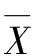
我們在學習二項分布、超幾何分布時，通常會將二者混淆，而且在解決實際問題時，也不知該使用何種分布.然而二項分布數學期望與超幾何分布數學期望是相同的，只需稍微修改一下超幾何分布模型就可以將之變為二項分布.

[1]吳海軍.超幾何分布的期望與二項分布的期望相等[J].中學數學教學參考，2015，12:93.

[2]毛曉峰.關于幾何分布的數學期望[J].數學教學研究，2015，10:56-57.

[3]黃太純.二項分布及其應用[J].高中生學習(高二版)，2012，12:32-34.

[4]洪奕迅.淺析高中數學中的二項分布與超幾何分布[J].新課程學習(中)，2013，03:66.

[5]燕建梁.超幾何分布及其推廣[J].太原師范學院學報(自然科學版)，2013，01:21-23，31.

[6]楊華,黃殷.是超幾何分布,還是二項分布[J].中小學數學(高中版)，2011，Z2:49-51.

[7]翟明娟.概率統計中有關超幾何分布的一個誤解[J].統計與決策，2014，03:26-28.

[8]余錦銀.二項分布的常見題型[J].高中生學習(高二版)，2014，01:31-33.

G632

B

1008-0333(2017)07-0010-02