高中物理動態平衡問題研究

江蘇省響水中學(224600)

徐廣飛●

高中物理動態平衡問題研究

江蘇省響水中學(224600)

徐廣飛●

物理過程的科學分析為成功解題奠定了基礎，如何在復雜的物理過程中準確把握解題信息，取決于對狀態信息的提取，正確挖掘物理問題中的特殊狀態是成功解題的關鍵.高中物理過程相對復雜，包括平衡、非平衡以及臨界狀態等，研究對象所處狀態與基本原理的合理對應是解決物理問題的紐帶.動態平衡狀態在高中物理過程中蘊含著多重量化信息，成功把握該狀態對解題具有舉足輕重的作用.

高中物理;動態平衡;力學方程

研究對象所處的狀態決定了基本原理的應用，是成功求解物理問題的關鍵.動態平衡問題是高中物理中的特殊平衡狀態，符合力學平衡方程，然而該狀態對于大多學生而言把握相對困難，需要構建臨界思維模式.物理思維的構建需要依托客觀物理過程，課堂誘導的方向必須以提取有用信息為目的，因此動態平衡問題的學習也是解題信息的攝取過程，是獲得定量關系的突破口.一般地，對物理教學中動態平衡問題的把握，更加考驗學生微觀思維的能力，要求學生對特定信息相對敏感，能夠在短時間提取有用信息，進而列出具體的物理方程，定量求解.

二、高中物理中典型的動態平衡問題

動態平衡的應用基礎在于對平衡狀態的認識，只有在平衡狀態下方可應用具體原理，進而將物理問題具體化.平衡狀態的顯著特征是研究對象滿足受力平衡特征，因此具備明確的力學規律，從整個過程來看，動態平衡可能是某非平衡過程的過渡點，因此也是物理求解中的“臨界點”或者“邊界條件”.一般而言，這種特殊的平衡態具有連續性，以及該狀態所體現的動力學特征具有連續性，是物體從一個狀態向另一狀態的過渡，因此該狀態科學分析能夠為物理求解提供更多的已知信息.

1.復合場中動態平衡問題求解

高中物理復合場問題是高考中的難點，涉及到多種場的共同作用，由于受力的復雜性，通常對該類問題的求解相對困難.然而，動態平衡狀態往往是復合場問題的突破口，因為研究對象通常在多種場的共同作用下處于平衡狀態，該狀態下研究對象所處的位置特性隨時間逐漸變化，亦即典型的動態平衡特征.

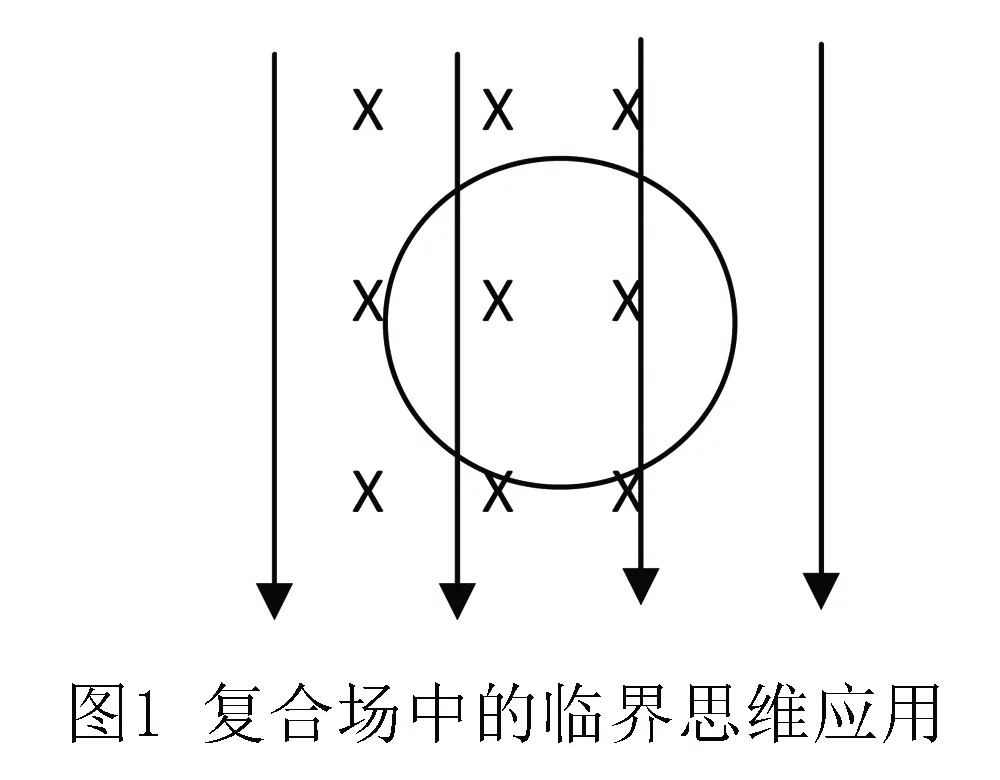
例1 質量為m的帶電微粒在電場、磁場以及重力場中恰好做勻速圓周運動，其軌跡處于磁場的垂直面內，并且其圓周運動半徑為R，試分析該帶電微粒的電荷類型？現已知：電場與重力場方向豎直向下，電場強度為E，重力加速度為g；磁場方向垂直紙面向里，強度為B.

分析 首先該問題屬于典型的復合場動態平衡問題，涉及到帶電微粒的運動軌跡等.如上所述，動態平衡問題的關鍵在于準確把握該特殊狀態的力學特性，“恰好”做圓周運動表明帶電微粒在電場力、重力、洛倫茲力的共同作用下處于平衡狀態，因此為了不使微粒豎直下落，必須存在豎直面內向上的力，并且該力與重力等大、反向、共線.顯然，由于洛倫茲力與運動軌跡垂直，不能平衡重力在豎直方向的作用效果，能夠提供重力的平衡力的只能是電場力，又已知電場方向豎直向下，據此可確定微粒的帶電類型.

2.斜面問題中的動態平衡

斜面問題是高中物理中常見的物理模型，通常研究對象為置于斜面上的物體，其難點在于如何準確給出研究對象的受力情況.對于該問題的處理，同樣應該在整合物理過程中尋求特殊“位置”，一般地，該類問題中的研究對象要么處于靜止，要么勻速直線運動，顯然對于這兩種狀態都能夠較為容易的列出具體的物理學方程.因此其關鍵在于如何科學理解特殊狀態，尤其對于動態平衡狀態的科學判定.斜面模型而言，物體與斜面間是否存在摩擦力決定了受力情況的復雜性.然而其基本理念依舊是力學平衡方程的求解.

例2 如圖2所示，質量為m的物體在傾角為θ的斜面上勻速下滑，已知物體與斜面間的動摩擦因數為μ，并且受到水平向右的推力F的作用，試列出該過程的平衡方程.

分析 “勻速下滑”是本題中唯一的動態平衡信息，勻速表明物體在垂直斜面方向與平行斜面方向上受到平衡力作用，因此可以具體列出平衡力方程.然而本題的關鍵在于目前已經明確物體沿斜面勻速下滑，亦即已經明確木塊具有沿著斜面向下的運動行為，物體與斜面間滑動摩擦力的方向為沿斜面向上，因此沿斜面向上的力包括推理F的分力與滑動摩擦力，而沿斜面向下的力只有重力的分力，據此可列出定量方程.該題中已知物體勻速下滑，因此該動態平衡簡化了物理問題，若題目表明該物體處于平衡狀態，而并非一定沿斜面勻速下滑，該情況相對復雜，既包括動態平衡也包括靜態平衡問題，尤其對于靜止狀態而言，雖然物體與斜面間無相對滑動，然而很可能存在沿斜面方向的運動趨勢，因此處于平衡狀態下必須對推力F存在限定條件.顯然，動態平衡狀態某種程度上可以簡化物理模型，為具體原理的應用提供理論框架.

平衡問題是物理學問題求解的突破口，尤其在復雜物理模型中，尋找恰當的平衡點是成功解題的關鍵.動態平衡問題能夠具體對應出研究對象所滿足的物理原理，明確物體受力情形.通常復合場問題以及斜面問題的動態平衡點，能夠幫助學者迅速找出力學關系，是成功解題的中樞紐帶.

[1]劉奇煜. 高中物理力學綜合題解題技巧探究[J]. 中學生數理化(嘗試創新班), 2014(6).

[2] 張丹. 高中物理力學教學生活化策略探討[J]. 經營管理者. 2016(27).

G632

B

1008-0333(2017)07-0069-01