煤層封存CO2性能的晶格理論模型及應用*

鄭新軍，岳高偉，霍留鵬，曾春林，梁為民

(河南理工大學 土木工程學院，河南 焦作 454000)

0　引言

煤體對氣體的吸附主要是微孔吸附，臨界溫度上下實驗吸附等溫線形狀均屬第Ⅰ種類型，但在超臨界條件下高壓時等溫線出現極值點[7-10]。現有的吸附等溫線方程都是單調增函數，其吸附理論不能成功地描述最大點以后的吸附行為[7]。多項式模型[11]和液相吸附移植模型[12]雖然在數學上成功地描述了具有最大點的吸附等溫線，但卻不能合理地解釋吸附機理[13-14]。如何建立恰當的模型以描述超臨界氣體的吸附等溫線，不僅可以揭示吸附機理，還能夠將氣體吸附存儲過程模型化，為工程實際提供所需的數據。周理[8]提出了超臨界吸附等溫線新的模型化方法，以吸附相密度為參數，采用D-A方程描述絕對吸附量，并用超臨界吸附的極限態作參考態，描述了所測得的具有最大點的吸附等溫線；鄭青榕[9]通過實驗數據的非線性回歸Toth方程參數后，可用來準確預測甲烷在Ajax活性炭上的過剩吸附等溫線。但前提是先確定吸附劑的孔徑分布(PSD)和吸附質分子吸附時的臨界孔寬；胡濤[10]提出以吸附相密度為參數，用L-F方程對甲烷在活性炭上超臨界高壓吸附等溫線數據回歸，模型回歸所得的參數能準確反映L-F方程的特性；Tang Xu[15]采用雙位Langmuir模型對甲烷在頁巖上吸附等溫線出現極大值的吸附行為，并對不同埋深的頁巖氣吸附量進行了理論預測；Ronny[16]基于晶格密度泛函理論模型，數值分析了CO2，CH4和N2及其混合物在1.2～8 nm狹縫形孔隙寬度上競爭吸附行為，而且對溫度、組分和密度影響的過剩吸附等溫線進行了研究；Ono S及Kondo S將晶格學、熱力學及蒙特卡洛等方法相結合，提出了用以表征分子吸附特征的晶格理論[17]；Aranovich等[18-21]將晶格理論的Ono-Kondo方程引入到氣體在微孔吸附劑內的吸附研究中，該模型能夠反映超臨界流體吸附等溫線的特殊性(即隨著壓力增加吸附量先增大后減小)；楊曉東[22]、鄭蓮慧[23]分別采用晶格理論對甲烷在活性炭和頁巖上的吸附特征進行了研究，在吸附平衡壓力較低時，預測結果精度較高，但未進行高壓時的研究。

為了更好地在煤層中封存CO2，開展CO2在煤上跨越臨界點的大范圍吸附尤為必要[24-25]。基于此，本文基于晶格理論模型，研究了不同溫度下大范圍吸附平衡壓力時不同變質程度煤對CO2的吸附特征，并對其吸附等溫線進行了理論預測。

1　晶格模型熱力學方程

多孔介質對氣體的吸附主要發生在微孔孔隙，在此，假設多孔介質微孔為狹縫，在狹縫寬度方向吸附N層氣體分子，如圖1所示。基于晶格理論，該模型由CO2分子和空位組成，CO2分子與孔壁之間的作用勢εs，相鄰CO2分子之間的作用勢εa，則在吸附平衡條件下把第i層中的一個CO2分子移到氣相中一個空位時，滿足[19]：

圖1　狹縫晶格一維模型Fig.1　One-dimensional of the slit pore lattice

(1)

式中：△H為焓變；T為氣體溫度；△S為熵變。

假設W1為第i層吸附分子數量配置而無窮遠處為空的幾率；W2為無窮遠處分子數量配置而第i層上為空的幾率，則熵變可表示為：

△S=klnW1-klnW2

(2)

式中：k為玻爾茲曼常數。

若該系統分子總體配置數為W0，由W1和W2與W0的比值可得：

W1/W0=xi(1-xb)

(3a)

W2/W0=(1-xi)xb

(3b)

式中：xi為第i層上氣體摩爾分數；xb為i→∞氣體摩爾分數。

將式(3)代入式(2)得：

△S=kln{[xi(1-xb)]/[ (1-xi)xb]}

(4)

焓變△H的立方晶格計算式為：

△H=-εa(xi+1+xi-1+4xi-6xb)

(5a)

當i=1時焓變△H表示為：

△H=-εs-εa(x2+4x1-6xb)

(5b)

將式(4)和式(5a)、(5b)代入式(1)，分別得[19,21,24-25]：

(6a)

(6b)

2　超臨界流體晶格模型分析

超臨界條件下，流體不可能凝結，在此引入微參量δi：

δi=(xi-xb)εa/kT

(7)

采用δi將式(6)線性化，可得：

δi+1+αδi+δi-1=0

(8)

式中：

α=-kT/[εaxb(1-xb)]-4

(9)

式(8)為二階線性差分方程，其通解為：

δi=C1ω1i+C2ω2i

(10)

式中：C1和C2為任意常數；ω1和ω2為特征方程(11)的根[23-24]：

ω2+αω+1=0

(11)

從式(11)可知ω1ω2=1。因此，其中一個的絕對值小于1，另一個絕對值大于1，則：

ω1=α/2-(α2/4-1)1/2

(12)

由式(9)，對于臨界流體可得：

α>2

(13)

在此條件下，式(11)的根ω1為實數，且為小于1的正值。

當i趨于無窮大時，δi趨于0，而∣ω2∣>1，因此由式(10)可得：

C2=0

(14)

為了確定常數C1，簡化式(6b)并假設：

|εs|>>|εa|

(15)

根據式(6b)和式(15)可得：

x1=xb/[xb+(1-xb)exp(εs/kT)]

(16)

由式(7)、式(10)和式(14)可得：

x1=xb+C1ω1kT/εa

(17)

由式(16)和式(17)可確定參數C1，整理得：

(18)

3　Gibbs 吸附理論

Gibbs吸附等溫線可表示為[12]：

(19)

式中：n為過剩吸附量，mmol/g；ns為表面單層理論飽和吸附量，mmol/g。

由式(7)、式(10)、式(14)得：

xi=xb+C1ω1ikT/εa

(20)

將式(20)代入式(19)得：

n=KC1ω1(kT/εa)/(1-ω1)

(21)

式中：K=ns。

由式(19)和式(21)，整理得：

(22)

對于微孔吸附劑，吸附層數i是有限的，而且，C2≠0，在對稱邊界x1=xN條件下，可得[12, 17]：

K=2ns(1-ω1N)/ (1+ω1N-1)

(23)

假設氣體分子為單層吸附，則N=2，且x1=x2，式(23)變為：

K=2ns(1-ω1)/ (1+ω1)

(24)

將式(24)代入式(22)，則氣體過剩吸附為：

(25)

氣體摩爾分數xb可表示為[25]：

xb=ρb/ρm

(26)

式中：ρb為氣相密度，mol/L；ρm為氣體最大吸附量時吸附相密度，mol/L。

將式(26)代入式(25)，整理得：

(27)

由式(9)、式(12)和式(27)組成氣相密度ρb與過剩吸附量n的關系，包含ns，ρm，εs及εa4個參數，通過試驗測試氣體吸附平衡壓力p和吸附量n的關系(吸附等溫線)可以擬合出4個參數的值。其中，氣相密度ρb可用氣體狀態方程得到：

ρb=pM/(ZRT)

(28)

式中：p為吸附平衡時瓦斯壓力；M為氣體分子量；R為氣體常數；Z為氣體在溫度、壓力條件下的壓縮系數，采用R-K方程式進行計算：

(29)

h=0.086 64pr/(ZTr)

(30)

式中：h為中間變量；Tr=T/Tc為CO2氣體的對比溫度；pr=p/pc為甲烷氣體的對比壓力；Tc為CO2臨界溫度，取31.1℃；pc為甲烷臨界壓力，取7.38 MPa。

4　煤體的CO2吸附試驗及分析

4.1　試驗裝置

采用高低溫吸附解吸試驗系統(如圖2)，該系統主要包括高低溫變頻控制單元、真空脫氣單元、吸附平衡單元、數據實時采集系統。溫度主要由高低溫變頻試驗箱控制，溫度范圍：-50℃～100℃；溫度偏差：≤±1℃；溫度波動度：±0.5℃。

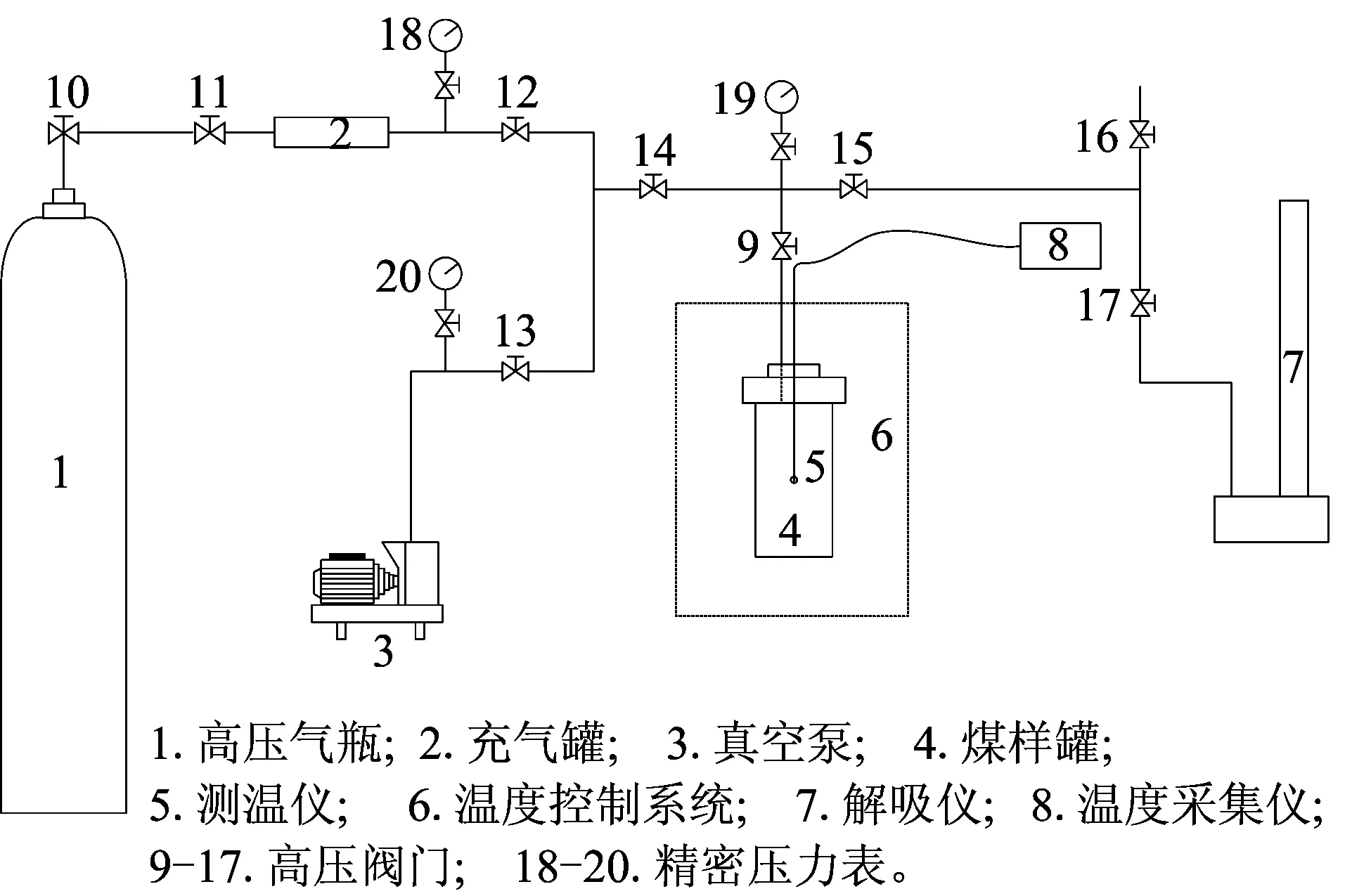
圖2　高/低溫吸附/解吸裝置示意Fig.2　Diagram of high/low temperature adsorption device

4.2　試驗過程

試驗煤樣取自山西屯留礦的瘦煤和寺河礦的無煙煤。在工作面取新鮮煤樣密封保存，而后送至實驗室，在室內煤樣經過破碎、粉碎和篩分過程，將煤制成符合GB/T19560-2004要求的60～80目的空氣干燥基煤樣。

按照GB/T 19560-2008《煤的高壓等溫吸附試驗方法》，對不同溫度煤樣的CO2吸附性能測試，試驗主要由以下4個過程：①煤樣制備：粉碎、篩選出粒度60～80目煤樣，并烘干； ②抽真空：采用真空泵對裝好煤樣的煤樣罐抽真空，直至煤樣罐內真空度低于10 Pa；③控溫：將煤樣罐放置在高低溫變頻控制箱中，設定試驗溫度，啟動高低溫變頻控制箱使煤樣維持在設定溫度；④不同充氣壓力下煤的瓦斯吸附量測試(吸附平衡時間不低于12 h，壓力讀數變化不超過0.01 MPa)。

4.3　煤的CO2吸附測試結果及分析

在CO2超臨界溫度下(305.15，308.15，318.15，328.15 K)，測試了2種變質程度煤對CO2的吸附規律，其等溫吸附曲線如圖3所示。

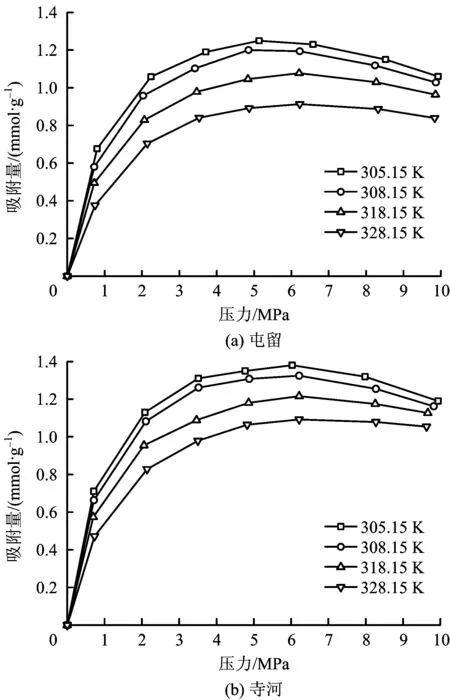
圖3　煤的CO2吸附性能測試Fig.3　Adsorption isotherm of CO2 in coal

從圖3中可看出，在壓力較低時，CO2在煤上的吸附等溫線為I型等溫線，但壓力較高時，CO2在煤上的過剩吸附等溫線出現了極大值，此后，測量吸附量隨著氣體壓力的增大而降低。這是因為在低壓/高溫下，氣相密度ρb與氣體最大吸附量時吸附相密度ρm相差極大，而xb(即ρb/ρm)遠小于1可忽略，因此無需區分過剩吸附量與絕對吸附量，即可認為二者相等。但隨著吸附壓力增大，氣相密度ρb與吸附相密度ρm的比值xb隨之增大，絕對吸附量隨壓力的增高而趨于飽和值。此后，測得的過剩吸附量n必然隨壓力(或主體氣相密度ρb)的繼續增長而下降。

為了采用晶格理論模型擬合CO2在煤上的吸附規律，采用R-K方程式(28)～(30)計算得到不同吸附平衡壓力下CO2氣相密度，其與吸附量的關系如圖4所示。在此，需要特別注意的是，雖然式(16)中|εs|>>|εa|，但εa卻不能忽略，因為若εa=0，即氣體分子之間沒有作用勢，僅存在氣體分子與孔壁之間的作用勢，游離氣體分子極易被孔壁吸附，被吸附的氣體分子量將增大，如圖4中虛線擬合。在低壓階段，忽略εa后的理論吸附量與實測吸附量差別不大，但隨著壓力增大，忽略εa后的理論吸附量與實測吸附量差別迅速增大。而且溫度越高，忽略εa后的理論吸附量與實測吸附量差別也越大。因此，在εa≠0情況下，采用式(9)、式(12)和式(27)組成的氣相密度ρb與過剩吸附量n的關系對CO2在煤上的吸附規律進行擬合，如圖4，擬合參數如表1。

圖4　CO2在煤上吸附規律的晶格理論模型擬合Fig.4　Lattice model fitting of CO2 adsorption law in coal

從表1中的擬合參數中可以看出，采用晶格理論模型(εa≠0)擬合CO2在煤上吸附出現極值的等溫線效果良好，相關系數均在0.99以上。而且對于同一煤質，煤表面單層理論飽和吸附量ns和氣體最大吸附量時吸附相密度ρm均為定值。同樣溫度下，CO2分子與孔壁之間作用勢εs遠大于相鄰CO2分子之間的作用勢εa；受溫度影響，CO2分子與孔壁之間的作用勢εs和相鄰CO2分子之間的作用勢εa也不同，且εs/k、εa/k與溫度T線性相關，如圖5～圖6所示，擬合參數如表2。

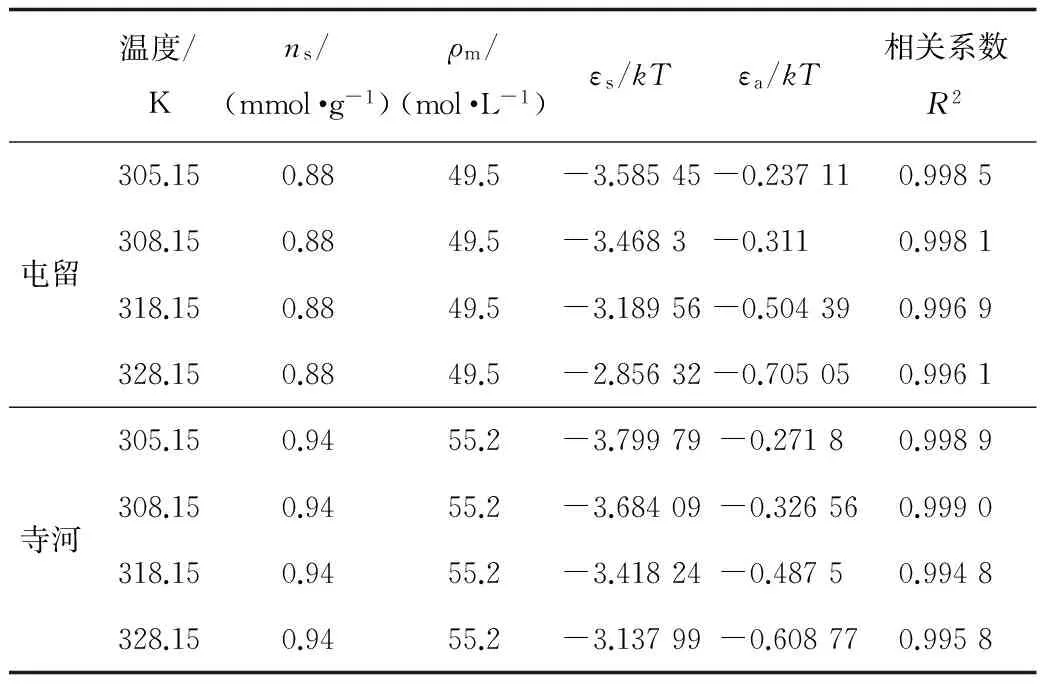
表1　晶格理論模型(εa≠0)擬合參數

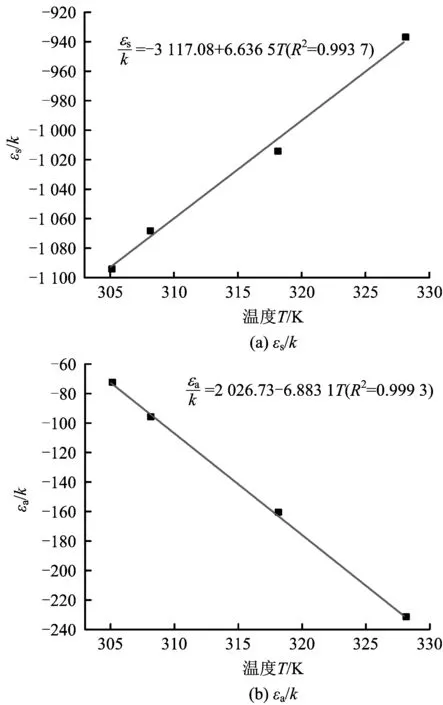
圖5　作用勢隨溫度變化規律(屯留煤樣)Fig.5　Variation of interaction potential (Tunliu coal samples)

圖6　作用勢隨溫度變化規律(寺河煤樣)Fig.6　Variation of interaction potential (Sihe coal samples)

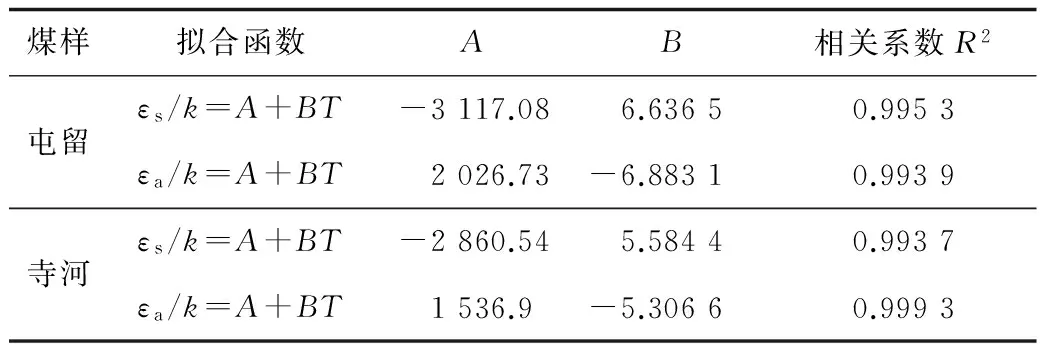
煤樣擬合函數AB相關系數R2屯留εs/k=A+BT-3117.086.63650.9953εa/k=A+BT2026.73-6.88310.9939寺河εs/k=A+BT-2860.545.58440.9937εa/k=A+BT1536.9-5.30660.9993

這是因為氣體分子在吸附劑表面放熱失去平均移動能而形成吸附相，溫度越高，吸附劑表面活性越大，使得氣體分子失去平均移動能越小，即εs越小；而分子之間的作用力使相互之間的距離到達勢能最小值，溫度越高，使得分子之間相互作用達勢能最小值的勢能越大，即εa越大。

4.4　煤的CO2吸附預測

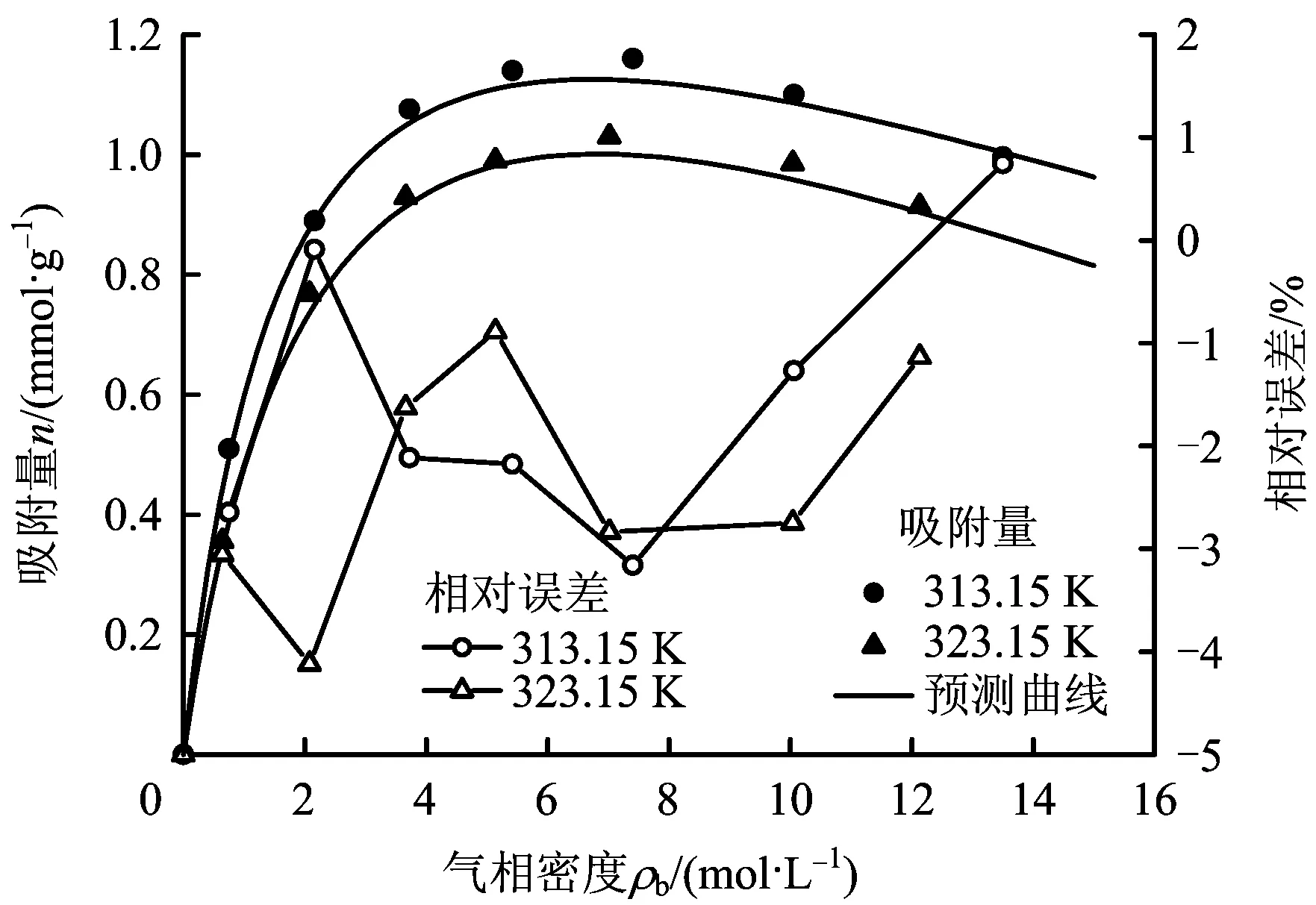
圖7　屯留煤樣吸附量預測及相對誤差Fig.7　Adsorption capacity prediction of Tunliu coal sample

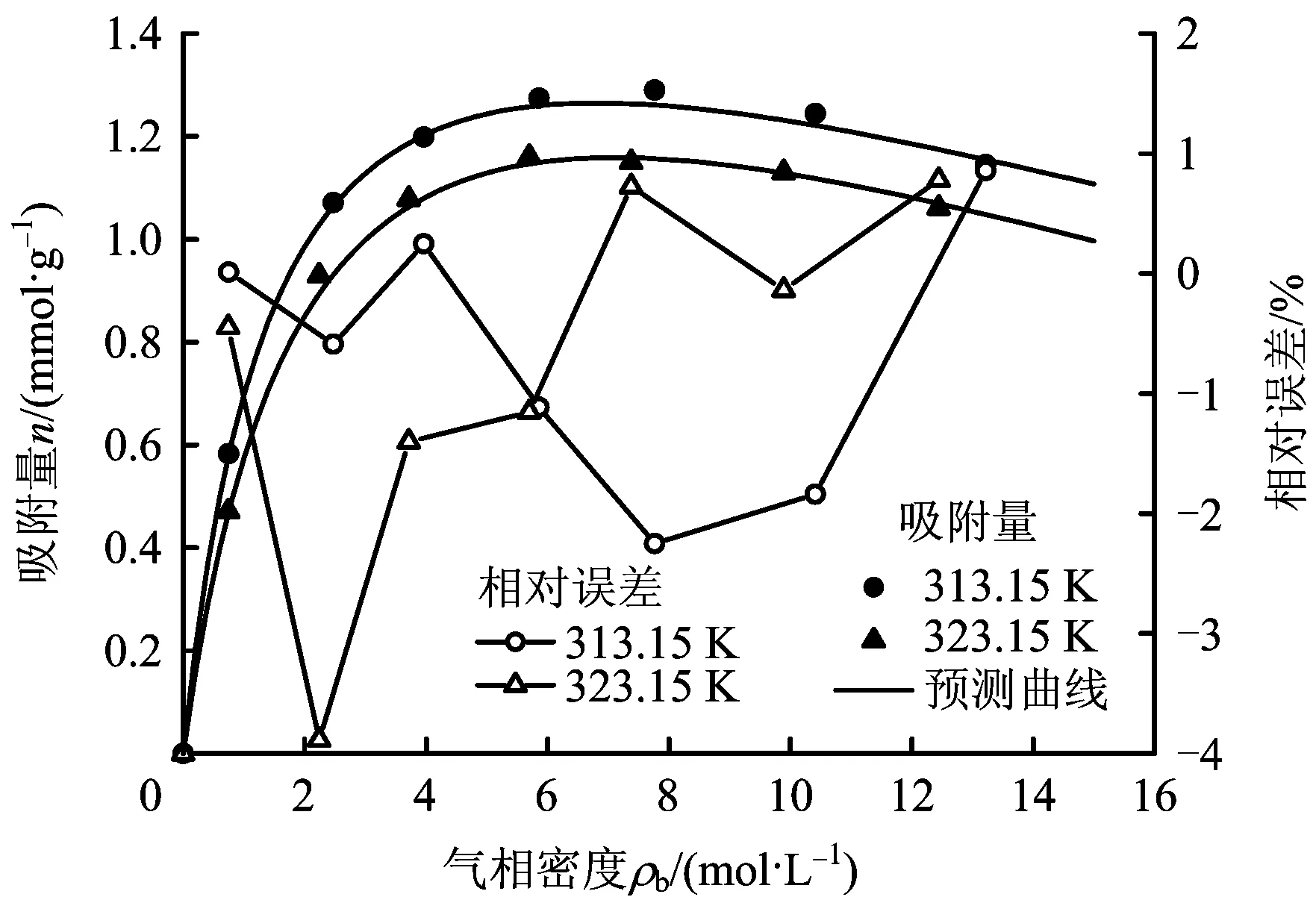
圖8　寺河煤樣吸附量預測及相對誤差Fig.8　Adsorption capacity prediction of Sihe coal sample

在不同溫度下，采用晶格理論模型(εa≠0)，對屯留礦瘦煤和寺河礦無煙煤的CO2的吸附等溫線進行預測，計算結果與實測結果如圖7和圖8，基于晶格理論模型的預測結果與實測結果基本一致，其相對誤差不超過5%。由此，采用晶格理論模型對吸附等溫線出現極大值情況(大范圍吸附平衡壓力)的預測是切實可行的。

5　結論

1)在壓力較低時，CO2在煤上的吸附等溫線為I型等溫線，但壓力較高時，CO2在煤上的過剩吸附等溫線出現了極大值，此后，測量吸附量隨著氣體壓力的增大而降低。

2)雖然CO2分子與孔壁之間的作用勢遠大于CO2分子之間作用勢，但εa卻不可忽略，否則壓力較大時，理論吸附量與實測吸附量誤差變大，而且，溫度越高，此誤差越大。

3)晶格理論模型(εa≠0)擬合CO2在煤上吸附出現極值的等溫線效果良好，相關系數均在0.99以上。

4)作用勢εs/k、εa/k與溫度T線性相關，相關系數均在0.99以上，εs/k與溫度正相關，而εa/k與溫度負相關。

5)采用晶格理論模型(εa≠0)對不同溫度下不同變質程度煤的CO2的吸附等溫線進行預測結果與實測結果基本一致，其相對誤差不超過5%。

[1]周來，馮啟言，秦勇. CO2和 CH4在煤基質表面競爭吸附的熱力學分析[J]. 煤炭學報，2011，36(8)：1307-1311.

ZHOU Lai, FENG Qiyan, QIN Yong. Thermodynamic analysis of competitive adsorption of CO2and CH4on coal matrix[J]. Journal of China Coal Society, 2011, 36(8): 1307-1311.

[2]楊宏民，魏晨慧，王兆豐，等. 基于多物理場耦合的井下注氣驅替煤層甲烷的數值模擬[J]. 煤炭學報，2010，35(S1)：109-114.

YANG Hongmin, WEI Chenhui, WANG Zhaofeng, et al. Numerical simulation of coal-bed methane displacement by underground gas injection based on multi-physics coupling[J]. Journal of China Coal Society, 2010, 35(S1): 109-114.

[3]崔永君，張群，張泓，等. 不同煤級煤對CH4、N2和CO2單組分氣體的吸附[J]. 天然氣工業，2005，25(1)：61-65.

CUI Yongjun, ZHANG Qun, ZHANG Hong, et al. Adsorption of different rank coals to single component cases[J]. Natural Gas Industry, 2005, 25(1): 61-65.

[4]范志強，SAM W，葉建平. 中國二氧化碳注入提高煤層氣采收率先導性試驗技術[M]. 北京：地質出版社，2008.

[5]White C M，Smith D H，Jones K L，et al. Sequestration of carbon dioxide in coal with enhanced coal bed methane recoverys a review[J]. Energy & Fuels，2005，19(3)：659-724.

[6]李全中，倪小明，王延斌，等. 超臨界狀態下煤巖吸附/解吸二氧化碳的實驗[J]. 煤田地質與勘探，2014，42(3)：36-39.

LI Quanzhong, NI Xiaoming, WANG yanbin, et al. The experimental study on the adsorption/desorption of carbon dioxide in the coal under supercritical condition[J]. Coal Geology & Exploration, 2014, 42(3): 36-39.

[7]Gregg S J, Sing K S W. Adsorption surface area and porosity[M]. London: Academic Press, 1982, 42-257.

[8]周理，李明，周亞平. 超臨界甲烷在高表面活性炭上的吸附測量及其理論分析[J]. 中國科學(B輯)，2000，30(1)：49-56.

ZHOU Li, LI Ming, ZHOU Yaping. Adsorption measurement and theoretical analysis of supercritical methane on high surface activated carbon[J]. Science in China (Series B), 2000，30(1)：49-56.

[9]鄭青榕，廖海峰，解晨，等. 超臨界甲烷在活性炭上的吸附平衡分析[J]. 燃料化學學報，2012，40(7)：892-896.

ZHENG Qingrong, LIAO Haifeng, XIE Chen, et al. Adsorption equilibrium of supercritical methane on activated carbon[J]. Joural of Fuel Chemistry and Technology, 2012, 40(7): 892-896.

[10]胡濤，馬正飛，姚虎卿. 甲烷超臨界高壓吸附等溫線研究[J]. 天然氣化工，2002，27(2)：36-40.

HU Tao, MA Zhengfei, YAO Huqing. Study on high pressure adsorption isotherms of supercritical methane[J]. Natural Gas Chemical Industry, 2002, 27(2): 36-40.

[11]Malbrunot P, Vidal D, Vermesse J, et al. Adsorption measurements of argon, neon, krytion, nitrogen and methane on activated carbon up to 650 MPa[J]. Langmuir, 1992, 8(2): 577-580.

[12]Aranovich G L, Donahue M D. Adsorption of supercritical fluids[J]. Journal of Colloid & Interface Science, 1996, 180: 537-541.

[13]Bénard P, Chahine R. Modeling of high pressure adsorption isotherms above the critical temperature on microporous adsorbents: application to methane[J]. Langmuir, 1997, 13: 808-813.

[14]Aranovich G L, Donahue M D. Determining surface areas from linear adsorption isotherms at supercritical conditions[J]. Journal of Colloid & Interface Science, 1997, 194: 392-397.

[15]Tang Xu, Nino Ripepi, Nicholas P Stadie, et al. A dual-site Langmuir equation for accurate estimation of high pressure deep shalegas resources[J]. Fuel, 2016, 185：10-17.

[16]Ronny Pini，Stefan Ottiger，Giuseppe Storti，Marco Mazzotti. Prediction of competitive adsorption on coal by a lattice DFT model[J]. Adsorption，2010，16: 37-46

[17]Ono S，Kondo S. Molecular theory of surface tension in liguids[M]. Berlin: Springer，1960.

[18]Aranovich G L, Donohue M D. Vapor adsorption on microporous adsorbents[J]. Carbon, 1995, 33(10):1369-1375.

[19]Aranovich G L, Donohue M D. Predictions of multilayer adsorption using lattice theory[J]. Journal of Colloid and Interface Science, 1997, 189: 101-108.

[20]Aranovich G L. Analysis of adsorption isotherms: lattice theory predictions, classification of isotherms for gas-solid equilibria，and similarities in gas and liquid adsorption behavior[J]. Journal of Colloid and Interface Science，1998，200: 273-290.

[21]Aranovich G L, Donohue M D. Vapor adsorption on microporous adsorbents [J]. Carbon, 2000, 38: 701-708.

[22]楊曉東, 林文勝, 鄭青榕, 等. 超臨界溫度甲烷吸附的晶格理論及實驗[J]. 上海交通大學學報，2003，37(7)：1137-1140.

YANG Xiaodong, LIN Wensheng, ZHENG Qingrong, et al. Latticetheory and experimental study of methane adsorption above the critical temperature[J]. Journal of Shanghai Jiao Tong University, 2003, 37(7): 1137-1140.

[23]鄭蓮慧，單鈺銘，鐘敬敏，等. 頁巖氣等溫吸附分子動力學特征研究[J]. 科學技術與工程，2014，14(33)：1-6.

ZHENG Lianhui, SHAN Yuming, ZHONG Jingmin, et al. Research of shale gas isotherm adsorption molecular dynamics characteristic[J]. Science Technology and Engineering, 2014, 14(33): 1-6.

[24]Grigotiy L A, Marc D D. Adsorption of supercritical fluids[J]. Journal of Colloid and Interface Science, 1996, 180：537-541.

[25]Mahmud S, Sayeed A M, Robert L R, eta al. Ono-Kondo lattice model for high-pressure adsorption: Pure gases[J]. Fluid Phase Equilibria，2010，299：238-251.