第二代完整穩(wěn)性癱船失效模式直接評估方法研究

王新宇，毛筱菲，歐 珊，吳銘浩

(武漢理工大學(xué) 交通學(xué)院船舶與海洋工程系， 湖北 武漢 430063)

第二代完整穩(wěn)性癱船失效模式直接評估方法研究

王新宇，毛筱菲，歐 珊，吳銘浩

(武漢理工大學(xué) 交通學(xué)院船舶與海洋工程系， 湖北 武漢 430063)

國際海事組織（IMO）在第二代完整穩(wěn)性規(guī)則的制定中，針對每一種失效模式提出了 3 層薄弱性衡準(zhǔn)。目前，癱船穩(wěn)性失效模式薄弱性衡準(zhǔn)已經(jīng)完成了第 1、2 層次的內(nèi)容，第 3 層次直接評估方案還未形成。本文基于 IMO 船舶設(shè)計(jì)與構(gòu)造分委會第一次會議（SDC1）提出的第 2 層薄弱性衡準(zhǔn)草案中關(guān)于癱船穩(wěn)性的相關(guān)內(nèi)容，采用單自由度橫搖運(yùn)動數(shù)學(xué)模型，編制數(shù)值計(jì)算程序，模擬船舶在極端惡劣條件下風(fēng)浪聯(lián)合作用的橫搖運(yùn)動，計(jì)算給定暴露時間船舶傾覆概率。將計(jì)算結(jié)果與 CEHIPAR2792 標(biāo)準(zhǔn)模型試驗(yàn)結(jié)果進(jìn)行對比，驗(yàn)證并分析數(shù)值方法的可行性，為確定該失效模式的直接評估方法提供參考。

第二代完整穩(wěn)性；癱船失效模式；數(shù)值模擬；直接評估；模型試驗(yàn)；蒙特卡羅模擬

0 引 言

IMO 目前正在制定船舶第二代完整穩(wěn)性衡準(zhǔn)相關(guān)草案，癱船穩(wěn)性薄弱性衡準(zhǔn)是 5 個薄弱性衡準(zhǔn)中的重要組成。癱船穩(wěn)性第 1 層和第 2 層薄弱性衡準(zhǔn)草案是由意大利和日本在 SDC1 會議上提出并得到通過的[1]。

當(dāng)船舶不滿足第 2 層薄弱性衡準(zhǔn)時須進(jìn)行第 3 層次的穩(wěn)性直接評估，目前評估方法尚未形成。美國[2]等國家要求癱船穩(wěn)性的直接評估方法至少考慮 5 個自由度（橫搖-橫蕩-垂蕩-縱搖-首搖）。但 5 個自由度計(jì)算模型復(fù)雜，特別是計(jì)算船舶傾覆概率時，為達(dá)到置信區(qū)間可信度要求，計(jì)算樣本量巨大，這導(dǎo)致目前多自由度計(jì)算模型目前尚難以執(zhí)行。

Kubo 等[3]討論了橫風(fēng)橫浪聯(lián)合作用下癱船橫搖運(yùn)動數(shù)值模擬方案，提供了單自由度直接模擬方法。該方案模型相對簡單，可以大幅縮短計(jì)算時間，經(jīng)過試驗(yàn)驗(yàn)證具有一定的參考性。

本文基于 SDC1/INF.6 中癱船穩(wěn)性失效模式薄弱性衡準(zhǔn)的單自由度橫搖運(yùn)動模型，對癱船穩(wěn)性第 3 層薄弱性衡準(zhǔn)直接評估方法進(jìn)行研究。通過建立癱船橫搖運(yùn)動單自由度非線性方程，分解求解無風(fēng)浪情況下的橫搖自由衰減運(yùn)動，以及規(guī)則波和不規(guī)則風(fēng)浪聯(lián)合作用下癱船橫搖運(yùn)動響應(yīng)。并進(jìn)行標(biāo)準(zhǔn)模型 CEHIPAR2792相應(yīng)試驗(yàn)，將試驗(yàn)數(shù)據(jù)與計(jì)算結(jié)果對比，為癱船穩(wěn)性直接評估方法研究提出建議。

1 單自由度橫搖運(yùn)動模型

考慮非線性的橫搖阻尼的橫風(fēng)橫浪下單自由度橫搖數(shù)學(xué)模型由如下非線性微分方程描述：

式中：左邊第 1 項(xiàng)為慣性力項(xiàng)；I’xx為船舶橫搖總慣性矩。試驗(yàn)?zāi)Ｐ偷臋M搖慣性矩可根據(jù)式（2）求出：

式（1）中第 2 項(xiàng)為阻尼項(xiàng)。本文基于標(biāo)準(zhǔn)模型 CEHIPAR2792 試驗(yàn)結(jié)果發(fā)現(xiàn)，當(dāng)使用線性項(xiàng)加平方項(xiàng)進(jìn)行擬合時，會出現(xiàn)線性項(xiàng)為負(fù)的顯然不符合實(shí)際情況的結(jié)果。當(dāng)換成線性項(xiàng)加立方項(xiàng)（如式（3）），能夠得到理想的擬合結(jié)果。

式（1）中第 3 項(xiàng)為回復(fù)力矩項(xiàng)，可由靜水力計(jì)算結(jié)果得到，通常用高次的奇次多項(xiàng)式進(jìn)行曲線擬合以便編制計(jì)算程序。

式（1）中的右端為外力作用項(xiàng)，本文計(jì)及非定常波浪和風(fēng)的共同作用。

通過以上分析確定橫搖運(yùn)動方程為：

1.1 回復(fù)力矩項(xiàng)

回復(fù)力矩項(xiàng)的處理主要是針對船舶在大角度橫搖時回復(fù)力矩項(xiàng)的非線性進(jìn)行精確的數(shù)值擬合。

本文的研究對象是標(biāo)準(zhǔn)模型 CEHIPAR2792，其主尺度如表 1 所示，試驗(yàn)研究船舶模型縮尺比為 1∶65。

表 1 CEHIPAR2792 模型主尺度Tab. 1 Main Dimensions of Model CEHIPAR2792

由 SDC1 INF.6 查得該船初始狀態(tài)正浮時的 GZ 曲線。通過幾何分析，確定貨物移動導(dǎo)致船舶具有初始的固定橫傾時的 GZ 曲線，其原理如圖 1 所示。

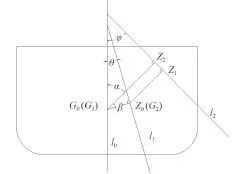
圖 1 貨物移動導(dǎo)致的橫傾使 GZ 改變Fig. 1 Cargo shift changes the GZ

如果不考慮貨物移動，橫傾 θ 角時，過重心 G0作l2的垂線，垂足為 Z0；橫傾 φ 角時，過重心 G0（G1）作 l3的垂線，垂足為 Z1。考慮貨物移動導(dǎo)致了船舶初始橫傾了 θ 角，重心從 G0移動到 G2。本試驗(yàn)中，θ 小于 10°，故考慮 Z0和 G2位置大致相同。則根據(jù)圖 1 中的幾何關(guān)系可以得到下式：

推出

得到貨物移動導(dǎo)致船舶重心發(fā)生改變后的船舶靜穩(wěn)性臂曲線表達(dá)式：

依據(jù)式（7）得到貨物移動導(dǎo)致不同初始固有橫傾狀態(tài)下的船舶 GZ 曲線如圖 2 示。該計(jì)算結(jié)果與 Kubo 等[2]的研究吻合。

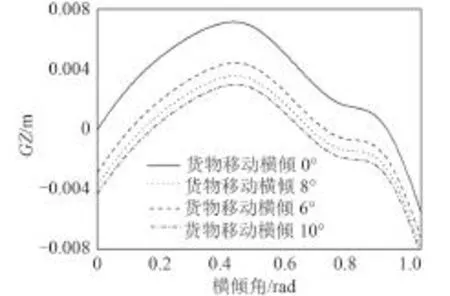
圖 2 不同固有橫傾狀態(tài)下的 GZ 曲線Fig. 2 GZ with different cargo shift

圖 3 初始狀態(tài)正浮時的 GZ 曲線擬合Fig. 3 Fitting of GZ

為了便于編制計(jì)算程序，使用最高 15 次的奇次多項(xiàng)式擬合 GZ 曲線，船舶正浮狀態(tài) GZ 曲線擬合結(jié)果如圖 3 所示。

其中，Ci如表 2 所示。

表 2 無貨物移動 GZ 曲線擬合系數(shù)Tab. 2 Fitting Coefficients of GZ without cargo shift

根據(jù)式（6），可以進(jìn)行相應(yīng)初始固有橫傾下的GZ 曲線計(jì)算，不需要單獨(dú)進(jìn)行擬合。

1.2 能量法求解衰減系數(shù)

橫搖阻尼力矩項(xiàng)的處理，是針對船舶在大角度橫搖時阻尼項(xiàng)產(chǎn)生的非線性進(jìn)行求解。通常采用模型試驗(yàn)得到船舶自由衰減曲線后，用能量法或消滅曲線法獲得橫搖阻尼力矩系數(shù)的方法。本文用線性加立方項(xiàng)的形式定義阻尼力矩項(xiàng)，并采用能量法求解[6]。

定義阻尼力矩為線性加立方項(xiàng)如下：

橫搖過程中三體船的總能量為：

根據(jù)能量守恒，損耗的能量用于抵消阻尼力矩所做的功，即

令

將式（8）和式（11）代入式（10）可得：

其中：等式的左邊為 δt 時間內(nèi)總能量的損失；右邊為阻尼力矩消耗的功。令

則式（12）可表示為：

式（14）可表示為矩陣：

式（15）中未知數(shù)只有 N1和 N3，其余均可用橫搖衰減曲線直接計(jì)算，應(yīng)用最小二乘法求解得到該矛盾方程的最小二乘解，取得阻尼力矩系數(shù) N1和 N3。

為了驗(yàn)證結(jié)果的正確性，令式（1）右端合外力矩項(xiàng)為 0，模擬船舶自由衰減，并與試驗(yàn)值對比如圖 4所示。

計(jì)算結(jié)果與試驗(yàn)采集數(shù)據(jù)吻合，驗(yàn)證了橫搖阻尼系數(shù)和靜穩(wěn)性曲線的計(jì)算準(zhǔn)確。

2 波浪力矩的計(jì)算

2.1 波浪條件

試驗(yàn)使用 ITTC 雙參數(shù)波浪譜，特征周期 T = 2.04 s，三一波高 H = 0.17 m，對應(yīng)實(shí)際海況為有義波高 11.04 m，特征周期 16.48 s。

圖 4 模擬自由衰減與實(shí)驗(yàn)值對比Fig. 4 Comparison of numerical and experimental free decay

隨機(jī)橫浪下單自由度橫搖數(shù)學(xué)模型由如下非線性微分方程描述：

方程兩邊同除以 I’xx，得

將式（17）寫成 2 個一階微分方程形式

在隨機(jī)波浪作用下，波浪激勵力矩由線性疊加原理得到。將隨機(jī)海浪處理為一系列具有隨機(jī)相位角的簡諧波的疊加。本文將根據(jù)給出的海浪譜，確定每個簡諧波的波浪要素及每個簡諧波引起的波浪干擾力矩，進(jìn)行疊加，得到任意瞬時總的波浪干擾力矩。

基于傅汝德-克雷洛夫和長波近似的假設(shè)上將橫浪中規(guī)則波的橫搖干擾力矩為：

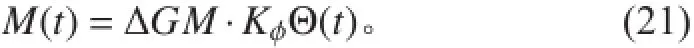
式中：K?為有效波傾系數(shù)；K?Θ（t）為有效波傾。

隨機(jī)波表示為一系列簡諧波的疊加，干擾力矩公式變?yōu)椋?/p>

式中：hi為波幅；λi為橫浪的波長；ωi為波浪頻率。

海浪譜就是海浪平穩(wěn)各態(tài)歷經(jīng)過程的能量在頻率域中的分布形式。式（20）又可寫為：

ITTC 雙參數(shù)譜：

式中：隨機(jī)相位角 εi在（0-2π）內(nèi)均勻分布；T 為特征周期；H1/3為三一波高。

圖 5 試驗(yàn)采用的 ITTC 譜Fig. 5 ITTC spectrum used in tests

2.2 有效波傾系數(shù) K

有效波傾角 αm和表面波傾角 α 存在如下關(guān)系[4]：

式中 αm0= K?α0，為有效波傾角的幅值，稱為有效波傾，它代表對船舶水下體積起作用的波傾，是波浪頻率的函數(shù)。

對于風(fēng)浪中的橫搖，其響應(yīng)主要集中在諧搖區(qū)的窄頻帶內(nèi)，通常用諧搖時的 K?代替整個頻率區(qū)間的K?不會引起太大誤差。Bulian 等[5]的研究認(rèn)為，頻率小的長波對船體的作用全部有效，有效波傾接近于1，而頻率高的短波作用在船體上幾乎可以忽略。將有效波傾系數(shù)簡化處理，在波長 λ = B/2 以下取定值，波長超過這個范圍后取 0。

本文根據(jù) SDC1/INF.6 中給出的 CEHIPAR2792 有效波傾測量值數(shù)據(jù)，在諧搖周期 ω = 0.342 rad/s 處取有效波傾系數(shù) 0.705，有效波傾系數(shù)取值如圖 6 所示。計(jì)算規(guī)則波中的運(yùn)動時取對應(yīng)波浪頻率下的有效波傾系數(shù)。

3 風(fēng)傾力矩的計(jì)算

風(fēng)傾力矩的計(jì)算式如下（包括定常風(fēng)和隨機(jī)陣風(fēng)）：

圖 6 簡化的有效波傾系數(shù)Fig. 6 Simplified effective wave slope coefficient

式中：ρa(bǔ)ir為空氣密度；Cm為風(fēng)壓傾側(cè)力矩系數(shù)[7]，取0.84；UW為定常風(fēng)速。U（t） 為 Davenport 風(fēng)譜[8]描述的非定常風(fēng)速；AL為水面以上船舶側(cè)投影面積；HC為風(fēng)力作用點(diǎn)距離水動力作用點(diǎn)的高度；χ（ω） 為陣風(fēng)影響系數(shù)。其受力分析如圖 7 所示。

計(jì)算采用下列公式：

當(dāng)風(fēng)速為 3 m/s（實(shí)際風(fēng)速 24.5 m/s）時，隨機(jī)風(fēng)的能量密度譜如圖 8 所示。

圖 7 橫風(fēng)作用示意圖Fig. 7 Diagram of the transversal wind

圖 8 風(fēng)速 3 m/s Davenport 風(fēng)譜Fig. 8 Davenport wind spectrum

將風(fēng)譜函數(shù)離散為 100 個頻率的疊加。風(fēng)的頻率ωwi=（0～1 rad/s），頻率間隔 δωw= 0.01 rad/s。

4 計(jì)算結(jié)果

4.1 初始固定橫傾

為模擬貨物移動導(dǎo)致的初始固定橫傾，在式（1）的右端加上一個導(dǎo)致船舶初始橫傾的初始力矩。

查靜穩(wěn)性臂曲線得到不同固定橫傾對應(yīng)值如表 3所示 ，并計(jì)算橫傾力矩。

表 3 不同初始橫傾角對應(yīng) GZ 值（模型）Tab. 3 Initial GZ under different cargo shift angle（model value）

4.2 規(guī)則波模擬及與試驗(yàn)的比較

規(guī)則波橫搖運(yùn)動方程：

式中：αm0為有效波傾角的幅值；Ω 為波浪頻率；K?為有效波傾系數(shù)；α0為有效波傾角；ζA為波面抬高；λ為波長；k 為波數(shù)。

模型在規(guī)則波中橫搖運(yùn)動時歷如圖 9 所示。統(tǒng)計(jì)規(guī)則波橫搖計(jì)算結(jié)果和試驗(yàn)結(jié)果對比如表 4 所示。

規(guī)則波單自由橫搖運(yùn)用模擬結(jié)果與試驗(yàn)結(jié)果基本吻合，誤差均小于 10%，滿足不規(guī)則波橫搖傾覆計(jì)算問題的精度要求。產(chǎn)生誤差的原因主要是單自由度計(jì)算未將其他自由度運(yùn)動考慮在內(nèi)，相比于實(shí)際運(yùn)動結(jié)果，理論結(jié)果必然存在誤差。

4.3 不規(guī)則波中傾覆概率計(jì)算

4.3.1 不規(guī)則波數(shù)值模擬

一般而言，隨機(jī)波浪被看作是平穩(wěn)隨機(jī)過程，可以通過不同周期和相位的余弦波疊加得到。本文采用ITTC 雙參數(shù)譜，大部分能量集中在 ωmin～ωmax間，本文略去頻率兩側(cè)總能量為 0.002 來確定波頻范圍。

將頻率分為 871 個規(guī)則波的疊加，波面方程為：

式中：ωi為規(guī)則波頻率；δω 為分解的規(guī)則波頻率間隔，取 0.01。

本文模擬模型試驗(yàn)有義波高 0.17 m、特征周期2.04 s。不規(guī)則波時歷數(shù)值模擬與試驗(yàn)測量船前波浪時歷對比如圖 10 所示，該種波浪情況下橫搖運(yùn)動時歷對比如圖 11 所示。不規(guī)則波三一波高統(tǒng)計(jì)值和橫搖運(yùn)動三一幅值的模擬與試驗(yàn)比較如表 5 所示。

從表 5 中可看出，編制的程序在模擬不規(guī)則波和船舶橫搖運(yùn)動時較準(zhǔn)確，不規(guī)則波以及運(yùn)動的準(zhǔn)確模擬是準(zhǔn)確計(jì)算的傾覆概率的保證。

圖 9 規(guī)則波中模型試驗(yàn)結(jié)果與模擬對比Fig. 9 Comparison of ship motion in regular waves between model tests and numerical results

表 4 規(guī)則波數(shù)值模擬與試驗(yàn)結(jié)果對比Tab. 4 Comparison of ship motion in regular waves between model tests and numerical results

表 5 波浪和船舶橫搖運(yùn)動統(tǒng)計(jì)值驗(yàn)證Tab. 5 Statistics of wave amplitudes and ship motion amplitudes

圖 10 數(shù)值模擬與試驗(yàn)測量波浪時歷對比Fig. 10 Comparison of irregular wave between model tests and numerical result

圖 11 數(shù)值模擬與試驗(yàn)測量船舶橫搖運(yùn)動時歷對比Fig. 11 Comparison of ship rolling on the irregular wave between model tests and numerical result

4.3.2 蒙特卡羅模擬

蒙特卡羅法計(jì)算傾覆概率通過時域計(jì)算，得到足夠的總樣本數(shù) N，根據(jù)計(jì)算得到的傾覆次數(shù) Nc 在總樣本數(shù)中的頻率來計(jì)算傾覆概率的統(tǒng)計(jì)值 P，即

為了驗(yàn)證統(tǒng)計(jì)值的可靠行，需要計(jì)算置信區(qū)間。假定 Pc 滿足二項(xiàng)分布：

式中 p 為真實(shí)概率，當(dāng)樣本足夠大，可認(rèn)為其符合正態(tài)分布。

概率 P 的置信區(qū)間可表示為：

為使置信區(qū)間可信度為 0.95，在給定環(huán)境條件下，船舶時域樣本為 1 000 次。

4.3.3 傾覆概率計(jì)算

船舶實(shí)際傾覆角在統(tǒng)計(jì)方法被中定義為進(jìn)水角、穩(wěn)性消失角和 50° 的較小者，本文取傾覆角為 50°。模擬船舶在橫風(fēng)橫浪中橫搖運(yùn)動暴露時間為 1 h。

本文進(jìn)行了試驗(yàn)海況三一波高 0.17 m，特征周期2.04 s，風(fēng)速 3 m/s，改變固定橫傾的傾覆概率計(jì)算，與 Kubo[2]中模型試驗(yàn)和數(shù)值模擬進(jìn)行對比如圖 12所示。

圖 12 船舶傾覆概率計(jì)算值和試驗(yàn)值對比Fig. 12 Comparison of capsizing probability between model test and numerical result

本文單自由度計(jì)算的結(jié)果與 Kubo 等計(jì)算的結(jié)果趨勢相近，本文計(jì)算結(jié)果偏大，在貨物移動導(dǎo)致橫傾 10°時與試驗(yàn)結(jié)果更加吻合。

5 結(jié) 語

本文基于單自由度橫搖運(yùn)動模型，對癱船風(fēng)浪作用下的穩(wěn)性進(jìn)行了直接評估。

通過幾何分析推導(dǎo)出船舶具有初始固定橫傾時回復(fù)力臂計(jì)算方法。探討了對于 CEHIPAR2792 標(biāo)準(zhǔn)模型大角度橫搖阻尼系數(shù)的確定方法，并將數(shù)值模擬與模型自由衰減試驗(yàn)對比。

將風(fēng)浪中橫搖運(yùn)動數(shù)值結(jié)果與船模的試驗(yàn)結(jié)果進(jìn)行對比，驗(yàn)證了單自由度數(shù)值方法的可靠性，得到以下結(jié)論：

1）船舶在不同初始橫傾下的靜穩(wěn)性曲線變化明顯，需重新計(jì)算，本文給出了計(jì)算方法。

2）采用能量法計(jì)算船舶橫搖阻尼系數(shù)能夠獲得良好的結(jié)果，采用一次項(xiàng)加三次項(xiàng)多項(xiàng)式模擬 CEHIPAR2792標(biāo)準(zhǔn)模型阻尼力矩的方法結(jié)果可靠。

3）不規(guī)則波計(jì)算中，從模擬計(jì)算時歷與實(shí)驗(yàn)值時歷圖比較來看，運(yùn)動幅值的誤差在可接受的范圍內(nèi)。這種單自由度直接模擬船舶在不規(guī)則風(fēng)浪中橫搖運(yùn)動是可行的。

4）有效波傾系數(shù)的準(zhǔn)確取值對波浪載荷計(jì)算具有重要影響，本文采用簡化模型，并使用了 SDC1/INF.6中的有效波傾值。在未來的研究中，有條件的情況下應(yīng)采用試驗(yàn)法測量船舶有效波傾系數(shù)，使計(jì)算結(jié)果準(zhǔn)確。

5）當(dāng)船舶具有貨物移動等造成的初始橫傾角時，同等海況下的傾覆概率增加。因此在實(shí)際航行中，貨物綁扎的檢查尤為重要，由于綁扎不牢、橫搖過大等原因?qū)е仑浳镆苿樱瑫勾皟A覆風(fēng)險大大增加，

6）單自由度計(jì)算未將其他自由度運(yùn)動（如升沉、橫蕩、首搖等）考慮在內(nèi)，相比于實(shí)際運(yùn)動結(jié)果，理論預(yù)報(bào)必然存在誤差。在今后的研究中，進(jìn)行多自由度耦合研究是該失效模式直接評估方法發(fā)展的必然趨勢。

[1]IMO SDC 1/INF, 6. Vulnerability assessment for dead-ship stability failure mode [C]. Italy and Japan, 2014.

[2]IMO SDC 1/INF, 8, ANNEX 16. Proposed amendments to part b of the 2008 is code to assess the Vulnerability of ships to the dead ship stability failure mode [C]. Italy and Japan, 2014.

[3]KUBO T, UMEDA N, IZAWA S, et al. Total stability failure probability of a ship in irregular beam wind and waves: model experiment and numerical simulation[C]//. Proceedings of the 11th International Conference on the Stability of Ships and Oceans Vehicles, 2009: 39-46.

[4]盛振邦, 劉應(yīng)中. 船舶原理[M]. 上海: 上海交通大學(xué)出版社, 2003.

[5]BULIAN G, FRANCESCUTTO A. A simplified modular approach for the prediction of the roll motion due to the combined action of wind and waves [J]. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 2004, 218(3): 189-212.

[6]李培勇, 馮鐵城, 裘泳銘. 三體船橫搖運(yùn)動[J]. 中國造船, 2003, 44(1): 24-30.

[7]湯忠谷, 韓久瑞, 施立人, 等. 海船風(fēng)壓試驗(yàn)研究[J]. 武漢水運(yùn)工程學(xué)院學(xué)報(bào), 1979(2): 1-18.

[8]DAVENPORT A G. The spectrum of horizontal gustiness near the ground in strong winds [J]. Journal of the Royal Meteorological Society, 1961, 87: 194-211.參考文獻(xiàn)：

A study on direct assessment method of dead ship failure mode of the second generation intact stability

WANG Xin-yu, MAO Xiao-fei, OU Shan, WU Ming-hao
(Wuhan University of Technology Department of Designing and Building for The Naval Architecture and Ocean Engineering, Wuhan 430063, China)

International maritime organization (IMO) is developing the second generation of the intact stability regulations, three levels of criteria will be proposed for each stability failure mode. The first and second levels of vulnerability criteria for dead ship mode have now been completed, but the third level vulnerability criteria, direct assessment, has not yet been formed. Direct-assessment method is the important content of the second generation intact stability currently. Based on the draft of the second level of vulnerability criteria of the dead ship mode-proposed on first meeting of the IMO sub-committee on ship design and construction (SDC1), using the mathematical model with one degree of freedom, the simulation programs of ship rolling in the beam wind and wave under extreme conditions are developed to calculate the ship-capsizing probability, the simulation results are compared with the model tests of the standard ship model CEHIPAR2792 to validate and evaluate the reliability of the numerical methods. Meanwhile, the references for the direct assessment method for this failure mode are provided to develop the method.

the second generation intact stability；dead ship failure mode；numerical simulation；direct assessment；model test；Monte Carlo simulation

1672 - 7619(2017)02 - 0012 - 07

10.3404/j.issn.1672 - 7619.2017.02.003

2016 - 08 - 08；

2016 - 08 - 26

工信部船舶第二代完整穩(wěn)性衡準(zhǔn)技術(shù)研究資助項(xiàng)目（2012[539]）

王新宇(1992 - )，男，碩士研究生，研究方向?yàn)榇八畡恿W(xué)。

U661.32

A