基于流固耦合效應的梯級泵站輸水管道振動特性分析

張建偉 王 濤 曹克磊 江 琦 喬鵬帥 許新勇

(華北水利水電大學水利學院， 鄭州 450011)

基于流固耦合效應的梯級泵站輸水管道振動特性分析

張建偉 王 濤 曹克磊 江 琦 喬鵬帥 許新勇

(華北水利水電大學水利學院， 鄭州 450011)

為解決管道結構固有振動特性分析中選取高精度流固耦合模型的方法問題，以景電工程中梯級泵站輸水管道為研究對象，運用附加質量法和直接耦合法原理，建立不同的流固耦合模型，對其進行固有模態特征提取，并將求解結果與SSI法模態辨識結果對比。結果表明：直接耦合法模型的結果與SSI法辨識結果吻合得較好，最大誤差為3.62%，同階次的計算精度均優于附加質量模型，頻率間隔小，彌補了附加質量模型出現的模態缺失現象；直接耦合模型的計算結果在模擬階數和精度方面都優于附加質量模型，能較好地反映管道結構的固有振動特性，可在復雜管系結構的動力特性分析中應用。

梯級泵站； 管道； 振動特性； 附加質量法； 直接耦合法； 模態參數辨識

引言

輸水管道在正常運行中，因受水流壓力脈動、泵站機組的動能傳遞、固-液間的耦合效應等因素影響而產生不同程度的振動，其中水體與管道結構間的相互耦合作用是引起管道系統振動的主要原因，長時間、無規律的流固耦合振動會導致管系及其附屬系統結構產生松動，嚴重時會造成災難性的破壞。

實際工程中常用于輸流管道振動特性分析的數值計算方法有特征線法、傳遞矩陣法、有限元法。其中，特征線法[1-2]僅限于單彎管之類的簡單管道模型，計算復雜管道流固耦合系統時，往往會因精度低而失真；傳遞矩陣法[3-4]則多應用在短直管道或低頻范圍內彎管管道的振動特性分析中；而有限元法[5-6]因具有適用范圍廣、計算精度高等優點被廣泛應用于求解各種復雜管道的流固耦合問題。運用有限元法進行輸流管道動力特性分析的關鍵是選取有效的固-液物理場處理方法。現有管系振動特性研究中進行固-液物理場處理的方法有附加質量法、順序耦合法和直接耦合法，不同物理場處理方法的實現過程及模擬精度有較大的差別，有待進一步研究。國內外學者采用不同的物理場處理方法從不同角度對輸流管道的動力特性進行了大量研究，并取得了一定的研究成果。MOUSSOU等[7]提出了采用附加流體質量法模型求解管道耦合動力特性的建議。馮衛民等[8]對不同約束條件下的流固耦合壓力管道模型進行了模態計算分析，結果表明流固耦合作用對輸流管道的運行有較大的影響，實際計算中不能忽略。李晨陽等[9]運用順序耦合法對考慮流固耦合效應的壓力管道動力特性及外聲場進行了仿真分析，為解決管道振動噪聲控制問題提供新的實現途徑。姬賀炯等[10]對比了直接耦合模型與附加質量法模型的分析結果，發現直接耦合法模型有新的振動形態出現，且有較高的計算精度。邱明星等[11]分析了不同影響因素下管道固有頻率的變化規律，建立了一種適用于航空發動機的充液管路固有頻率計算模型。

上述基于輸流管道振動問題的研究多數局限于短直或無岔管影響的簡單管式結構，對于有效的固-液物理場處理方法在復雜管式結構(變管徑、有岔管等)動力特性方面的應用研究卻很少。本文以景電工程二期三泵站2號管道為研究對象，對不同的流固耦合模型進行模態計算分析，并將計算結果與隨機子空間識別(Stochastic subspace identification，SSI)計算的模態參數對比，評判出適合復雜管式結構分析的流固耦合模型，以期為后續研究者選取合理的動力計算模型提供理論參考。

1 基本理論

1.1 附加質量法

附加質量法是一種考慮水體對結構作用的簡化動力分析計算方法，它將動水壓力等效為質量附加在結構上，達到等效的動力響應。由于方法簡單、計算方便，這種方法的應用十分廣泛，在大壩、橋梁、儲液罐等的有限元模擬中都有采用[12-14]。

管道結構的運動微分方程為

(1)

考慮水體對管道附加質量的系統振動有限元方程為

(2)

式中Ma、Ca、Ka——由水體作用引起的附加質量、附加阻尼、附加剛度矩陣

理想流體阻尼力比較小，可以忽略，如果同時忽略水體對于結構剛度的影響，即Ka=O(O為零矩陣)，式(2)可以簡化為

(3)

1.2 直接耦合法

假設液體是無粘、可壓縮的理想液體，沒有不規則流動，平均密度和壓力相同。液體的動量方程和連續性方程可以簡化為聲場波動方程

(4)

其中

式中C——流體介質中的聲速ρ0——流體平均密度k——流體的體積模量P——聲壓t——時間

通過Galerkin法對方程離散化就可以得到單元矩陣；在式(4)兩邊同乘一個聲壓變化值δP，然后在整個流體域內積分。根據假設，在界面法向上，流體聲壓梯度與結構的法向加速度和流體密度的乘積大小相同。再將上述關系代入積分式中得到

(5)

式中V——整個流體域S——流體與結構的交界面n——交界面的單位法向量L、LT——梯度和散度的矩陣

將式(5)對聲壓和結構的位移進行離散，并表示為

(6)

其中

為考慮流固交界面處的能量損耗，需在方程中加入一個損耗項，變為考慮交界面能量損耗的聲波離散方程，即

(7)

其中

在流固耦合問題中，將流固交界面的流體壓力荷載加入到結構有限元方程中，即

(8)

其中

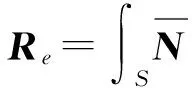
(9)

最后合并結構振動方程和流體波動方程可以得到[15]

(10)

其中

KPs=-Re

2 工程實例

2.1 工程概況

景泰川電力提灌工程(簡稱景電工程)是一項大型梯級泵站提水灌溉工程，具有高揚程、大流量等特點，整個工程共3部分組成：景電一期工程、景電二期工程及景電二期延伸工程。其中景電二期工程地跨甘肅省景泰、古浪兩縣，灌區內常年干旱、多風沙，嚴重制約當地農林經濟的發展。該工程總干渠長99.62 km，泵站13級，渠道建筑物總計達298座，提水設計流量18 m3/s，總揚程713 m，設計灌溉面積3.47×104hm2。

景電工程二期三泵站2號管道為多機單管布置形式，這種布置形式在大型泵站中較多采用，且2號管在運行過程中存在明顯的振動現象，并伴有較大的噪聲，因此以該管道為對象研究振動問題具有代表性和普遍性。2號管道的平面布置如圖1所示。

圖1 2號管道平面布置圖Fig.1 Plane layout of No.2 pipeline1.鎮墩 2、6.進水口 3.墻體 4、5.機組 7.出水口

2.2 原型管道模態參數辨識

以2號壓力管道為研究對象進行工作模態參數識別：試驗采用耐沖擊的DP型地震式低頻振動傳感器，該拾振器設有小速度、中速度、大速度和加速度4個擋位，具有體積小、質量輕、使用方便、動態范圍大和一機多用的特點，根據管道的工作振動特點，選用中速度擋位，該擋位下水平拾振器的靈敏度范圍在7.394～7.543 V·s/m之間，垂直拾振器的靈敏度范圍在6.729～6.920 V·s/m之間。 18個拾振器3個一組，分為6組，布置在管道的6個測點上，每個測點的3個拾振器分別沿管道的徑向、軸向和鉛垂方向布置，現場測點布置和壓力管道測點具體布置如圖2所示。

圖2 現場測試和測點平面布置圖Fig.2 Picture of field test and measuring point layout

圖3 測點13降噪前后信號時程圖Fig.3 Time history curves comparison of signal at point 13

以4號、5號機組正常運行為實測工況，測試采樣頻率204.8 Hz，采樣時間為1 500 s。基于數據驅動的隨機子空間算法是近年來常用的辨識精度較高的模態參數辨識方法[16-17]，采用該辨識方法對現場實測數據進行處理得到管道結構的動力特性。為提高模態辨識精度，減少虛假模態干擾，首先利用小波閾值-EMD聯合濾波[18]技術處理實測數據，凸顯結構振動特性，圖3為測點13降噪前后時程線，由圖3可知信號經濾波處理后，大部分強噪聲基本濾除；然后將降噪后的信號構造Hankel矩陣，利用奇異熵增量理論確定系統階次，如圖4所示，當奇異譜階次為12階時，對應的奇異熵增量開始逐漸趨于平穩，剔除系統非模態項和共軛項之后，得到管道系統有效振動階次為6階。

為避免某一時間段內數據計算結果的偶然性，對同工況下實測的1 500 s數據，每隔100 s選取50 s數據進行SSI辨識，共得10組模態辨識結果，每一組數據分別計算得到前6階模態頻率，利用穩定圖法[19]對這10組計算結果求每一階頻率均值。穩定圖橫坐標為頻率，縱坐標為試驗組數，在穩定圖中標記每一組模態識別得到的前6階頻率，將10組模態辨識結果依次標記完成，頻率穩定圖如圖5所示。根據圖5標記的10組試驗前6階頻率結果，計算每一階頻率均值作為管道結構最終結果。

圖4 奇異熵增量隨奇異譜階次變化曲線Fig.4 Curve between increment of singular entropy and order

圖5 管道模態頻率穩定圖Fig.5 Stabilization diagram of modal frequency of pipe

2.3 管道結構有限元建模

結合工程設計資料，采用附加質量原理和直接耦合法原理，建立了2種不同耦合形式的管道結構三維有限元模型，管道直接耦合法模型及不同水體耦合形式斷面圖如圖6、7所示。直接耦合法模型采用solid185三維實體單元模擬管道結構，內部流體介質則采用fluid30三維聲學流體單元模擬。考慮到直接耦合法固-液物理場處理方法的特殊性及計算的難易程度，流體模擬時需對fluid30單元屬性進行設置[20]：與管道內壁面直接接觸的耦合層單元(fluid30)屬性設為present，表示fluid30為8節點六面體單元，且每個節點有3個平移自由度和1個壓力自由度；不與實體結構接觸的流體單元屬性設為absent，則節點自由度的個數降為1，僅有壓力自由度。耦合計算時流固兩相介質間的相互作用需通過FSI耦合界面實現，使耦合面上單元(結構和流體)節點具有相同的位移和壓力。附加質量模型中管道結構的模擬方法與直接耦合法一致，水體耦合效應通過在管壁節點上添加mass21單元實現。為提高計算結果的精確度，流固耦合模型均采用掃略法和映射法進行網格劃分。直接耦合法模型共有44 516個單元，其中結構單元7 412個，流體單元37 104個；附加質量模型共有單元12 641個(結構單元6 040個，mass21單元6 601個)。

圖6 2號管道幾何模型Fig.6 Geometric model of No.2 pipeline

圖7 流固耦合模型斷面圖Fig.7 Sectional views of fluid-solid interaction model

邊界條件設置：管道原型設計中2個進口通過墻體與廠房內的泵機連接、出口一端伸入鎮墩(圖1)，模擬計算中均將其視為固定端約束。

模型參數選取：壓力鋼管密度為7 850 kg/m3，彈性模量206 GPa，泊松比0.25；管內三維聲學流體的聲波傳播速度為1 460 m/s，密度為1 000 kg/m3。

2.4 模態計算與試驗驗證分析

模態計算分析能夠有效地反映出結構的固有動力特性，其結果是結構安全評價的依據，也是結構動力分析的基礎。研究中依據不同耦合模型的耦合振動原理，運用不同的模態求解方法進行結構的固有模態參數提取。附加質量模型采用高精度、適用范圍廣、低耗時的分塊蘭索斯法，而直接耦合法模型則依據自身耦合振動特性采用運行程序簡單、運算量小、計算精度高的非對稱算法。不同模型的模態計算結果如表1所示。f0為空管模型的模態頻率，f1為含流體但不考慮流固耦合作用模型的模態頻率，f2為附加質量模型的模態頻率，f3為直接耦合法模型的模態頻率，f4為SSI方法識別的試驗模態頻率。δ1為附加質量模型頻率與實測頻率的誤差，δ2為直接耦合模型頻率與實測頻率的誤差。

由表1中可知：不考慮流固耦合作用時管道結構模態頻率與空管管道的模態頻率差別不大，且明顯都大于考慮流固耦合作用管道的模態頻率，研究結果與文獻[21]一致。考慮流固耦合后管道結構基頻降幅達到了50%左右，說明固-液物理場間的相互耦合作用對結構固振動特性有較大影響，仿真計算中若不予考慮則會降低模擬結果的可信度、精確度，實際工程動力特性分析中不能忽略。

表1 無水管道模型、附加質量模型、直接耦合法 模型模態頻率以及SSI分析頻率對比Tab.1 Comparison of vacuum pipeline model, additional mass model, direct coupling model and SSI

2種耦合模型采用不同的固-液物理場處理方法來反映水體對結構的作用，直接耦合法模型的計算結果與辨識結果吻合度高，且誤差精度也能滿足工程要求，而附加質量法模型的結果較實測值有較大偏差，說明直接耦合法能夠很好地解決固-液間的耦合效應，可在管道結構的動力特性分析中應用。

與SSI法模態辨識結果對比，附加質量法模型的頻率誤差為3.42%～13.43%；而直接耦合法的誤差為1.08%～3.62%，同階次誤差精度均比附加質量法高，最大誤差相差9.81個百分點。對不同結果進行誤差分析知：直接耦合法模型的計算精度更高，與辨識結果擬合得更好。

相比直接耦合法模型計算結果，附加質量模型出現了低階模態缺失現象，不利于管道結構正常運行工況下的健康評估。研究中模態缺失現象與文獻[10]的規律一致，驗證了固-液耦合模型的正確性。限于篇幅，僅分析了結構的前6階模態，更高階次的缺失現象不再給予說明。模態缺失的主要原因：附加質量法僅能模擬水體對結構的一階效應，不能真實反映流-固兩相介質之間的相互作用，且得出的各階固有頻率間隔較大，相鄰模態重疊較少。

直接耦合法和附加質量法管道模型的前6階振型如圖8所示。

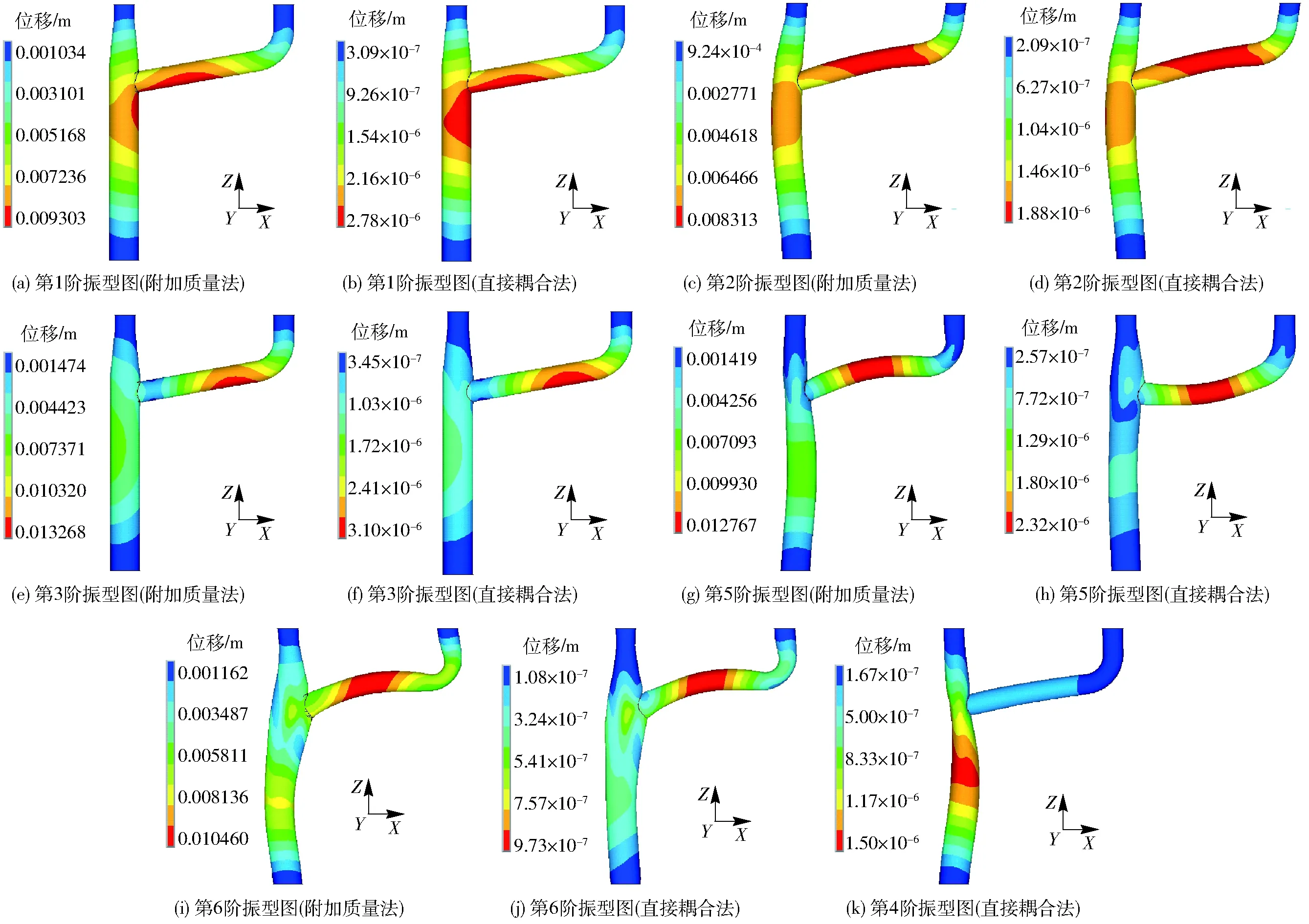
圖8 管道結構振型圖Fig.8 Model diagrams of pipe structure

對比不同耦合模型的振型圖知：

附加質量模型的振型形態與空管振型形態(限于篇幅，沒有列出)基本一致，該現象主要是因附加質量模型只是一種簡單的線性流固耦合模型，不能夠準確反映結構的振型形態；直接耦合法模型新增的第4階振型在管道主管段中部產生了水平方向振動，且振動形態與第2階類似，結構固有特性分析中應給予重視。

2號管道的振型主要以橫向振動為主，但相對于簡單直管的橫向振動復雜了許多。管道結構的主振區位于主支管交接的部位(第1階振型)，振幅最大，對結構的安全不利。實際工程中應在該處設置鎮墩來限制因管內水流突變所引起的振動和位移；但該管道主支管交接部位距離墻體較近，考慮溫度應力作用并沒有設置鎮墩，輸水期間需通過有效的減振措施保證管系結構的長久、安全運行，同時也為同類工程的減振設計提供理論參考。

3 結論

(1)與SSI法模態辨識試驗結果對比，附加質量法模型的頻率誤差為3.42%～13.43%；而直接耦合法的誤差為1.08%～3.62%，且同階次誤差精度均比附加質量法高，最大誤差相差9.81個百分點。對不同結果進行誤差分析知：直接耦合法模型的計算精度更高，與辨識結果擬合得更好。

(2)直接耦合法模型避免了固有動力特性分析中的模態缺失現象，能更精準地反映結構的固有振動特性。

1 楊超, 范士娟. 管材參數對輸液管流固耦合振動的影響[J]. 振動與沖擊, 2011, 30(7):210-213. YANG Chao, FAN Shijuan. Influence of pipe parameters on fluid-structure coupled vibration of a fluid-conveying pipe [J].Journal of Vibration and Shock, 2011, 30(7):210-213.(in Chinese)

2 KERAMAT A, TIJSSELING A S, HOU Q, et al. Fluid-structure interaction with pipe-wall viscoelasticity during water hammer[J]. Journal of Fluids & Structures, 2012, 28(1):434-455.

3 焦宗夏, 華清, 于凱. 傳輸管道流固耦合振動的模態分析[J]. 航空學報, 1999,20 (4):316-320. JIAO Zongxia, HUA Qing, YU Kai. Frequency domain analysis of vibrations in liquid-filled piping systems[J]. Acta Aeronauticaet Astronautica Sinica,1999, 20(4):316-320.(in Chinese)

4 張智勇, 沈榮瀛, 王強. 充液管道系統的模態分析[J]. 固體力學學報, 2001, 22(2):143-149. ZHANG Zhiyong, SHEN Rongying, WANG Qiang. The modal analysis of the liquid-filled pipe system[J].Chinese Journal of Solid Mechanics, 2001, 22(2):143-149.(in Chinese)

5 王世忠, 于石聲, 趙陽. 流體輸送管道的固-液耦合特性[J]. 哈爾濱工業大學學報, 2002, 34(2):241-244. WANG Shizhong, YU Shisheng, ZHAO Yang. Solid-liquid coupling characteristics of fluid-conveying pipes[J]. Journal of Harbin Institute of Technology, 2002, 34(2):241-244.(in Chinese)

6 葉紅玲, 邵沛澤, 陳寧,等. 流固耦合輸流管系統的動力學分析及參數影響[J]. 北京工業大學學報, 2015，41(2):167-173. YE Hongling, SHAO Peize, CHEN Ning, et al. Dynamic analysis and parameters’ influences on fluid-structure interaction in a fluid-filled pipes system [J].Journal of Beijing University of Technology, 2015，41(2):167-173.(in Chinese)

7 MOUSSOU P, VAUGRANTE P, GUIVARCH M, et al. Coupling effects in a two elbows piping system[C]∥Proceedings of the 7th International Conference on Flow Induced Vibrations, 2000:579-586.

8 馮衛民, 宋立, 肖光宇. 基于ADINA的壓力管道流固耦合分析[J]. 武漢大學學報：工學版, 2009, 42(2):264-267. FENG Weimin, SONG Li, XIAO Guangyu. Coupling analysis of fluid-structure interaction in pressure pipes based on ADINA[J].Engineering Journal of Wuhan University, 2009, 42(2):264-267.(in Chinese)

9 李晨陽, 李維嘉, 李鐵成. 流固耦合作用下液壓管道聲場數值仿真[J]. 艦船科學技術, 2011, 33(4):25-29. LI Chenyang, LI Weijia, LI Tiecheng. Numerical analysis of sound field of hydraulic pipe considering fluid-structure interaction[J]. Ship Science and Technology, 2011, 33(4):25-29.(in Chinese)

10 姬賀炯, 白長青, 韓省亮. 輸流管道耦合動力特性分析[J]. 噪聲與振動控制, 2013,33(5):10-14. JI Hejiong, BAI Changqing, HAN Shengliang. Analysis of dynamic characteristics of fluid-structure interaction in fluid-filled pipes[J]. Noise and Vibration Control, 2013,33(5):10-14.(in Chinese)

11 邱明星,陳志英,王建軍,等. 充液管路固有頻率試驗與計算分析[J].推進技術, 2013,34(11):1537-1542. QIU Mingxing, CHEN Zhiying, WANG Jianjun, et al. Experiment and numerical analysis of natural frequency for liquid-filled pipe[J]. Journal of Propulsion Technology,2013,34(11):1537-1542.(in Chinese)

12 劉煥忠, 李青, 莊茁,等. 發展附加質量模型應用于儲液罐的動力分析[J]. 工程力學, 2005,22(增刊1):161-171. LIU Huanzhong, LI Qing, ZHUANG Zhuo, et al. Development of added mass model and application to dynamic analysis of cylindrical tanks [J]. Engineering Mechanics, 2005,22(Supp.1):161-171.(in Chinese)

13 王銘明, 陳健云, 徐強,等. 不同高度重力壩動水壓力分析及Westergaard修正公式研究[J]. 工程力學, 2013，30(12):65-70. WANG Mingming, CHEN Jianyun, XU Qiang, et al. Study on different height gravity hydrodynamic pressure and Westergaard correction forumla[J]. Engineering Mechanics, 2013，30(12):65-70.(in Chinese)

14 張國明, 宋波. 動水壓力對深水橋梁性能設計的影響[J]. 北京科技大學學報, 2009, 31(9):1086-1094. ZHANG Guoming, SONG Bo. Effect of hydrodynamic pressure on performance-based design of a deepwater bridge[J]. Journal of University of Science and Technology Beijing, 2009, 31(9):1086-1094.(in Chinese)

15 白長青,周進雄,閆桂榮. 截錐型薄壁結構聲振耦合動力特性分析[J]. 應用力學學報,2010,27(1):28-32. BAI Changqing, ZHOU Jinxiong, YAN Guirong. Dynamic characteristics analysis of a truncated conical thin-walled shell with acoustic-structure coupling[J]. Chinese Journal of Applied Mechanics, 2010, 27(1): 28-32.(in Chinese)

16 張建偉,張翌娜,趙瑜.泄流激勵下水工結構應變模態參數時域識別研究[J].水力發電學報, 2012,31(3):199-203. ZHANG Jianwei，ZHANG Yi’na，ZHAO Yu. Study on strain modal parameters identification of hydraulic structure in time domain under discharge excitations[J]. Journal of Hydroelectric Engineering，2012，31(3)：199-203.(in Chinese)

17 常軍,張啟偉,孫利民. 穩定圖方法在隨機子空間識別模態參數中的應用[J]. 工程力學,2007,24(2):39-44. CHANG Jun, ZHANG Qiwei, SUN Limin. Application of stabilization diagram for modal parameter identification using stochastic subspace method[J]. Engineering Mechanics,2007,24(2):39-44.(in Chinese)

18 張建偉,江琦,朱良歡,等.基于改進HHT的泵站管道工作模態辨識[J].農業工程學報,2016,32(2):71-76. ZHANG Jianwei, JIANG Qi, ZHU Lianghuan, et al. Modal parameter identification for pipeline of pumping station based on improved Hilbert-Huang transform[J]. Transactions of the CSAE, 2016,32(2):71-76.(in Chinese)

19 張建偉,康迎賓,張翌娜,等. 基于泄流響應的高拱壩模態參數辨識與動態監測[J].振動與沖擊,2010,29(9):146-150. ZHANG Jianwei, KANG Yingbin, ZHANG Yi’na, et al. Modal parameter identification and dynamic monitoring of high arc dam under vibration response induced by flow discharge [J]. Journal of Vibration and Shock, 2010,29(9):146-150.(in Chinese)

20 姬賀炯, 白長青, 韓省亮. 輸流管道動力有限元建模及實驗研究[J]. 應用力學學報, 2013,30(3):422-427. JI Hejiong, BAI Changqing, HAN Shengliang. Dynamic finite element modeling and experimental research of the fluid-filled pipeline[J]. Chinese Journal of Applied Mechanics, 2013,30(3):422-427.(in Chinese)

21 俞樹榮,馬璐,余龍. 彎曲輸流管道流固耦合動力特性分析[J]. 噪聲與振動控制,2015,35(4):43-47. YU Shurong,MA Lu,YU Long. Analysis of dynamic characteristics of fluid-structure interaction in curved infusion pipelines[J]. Noise and Vibration Control,2015,35(4):43-47.(in Chinese)

Analysis of Water Pipeline Vibration Characteristics in Cascade Pumping Station Based on Fluid-Solid Coupling Interaction

ZHANG Jianwei WANG Tao CAO Kelei JIANG Qi QIAO Pengshuai XU Xinyong

(CollegeofWaterConservancy,NorthChinaUniversityofWaterConservancyandElectricPower,Zhengzhou450011,China)

As the basic carrier of long-distance inter-basin water conveyance project of pressure piping, pressure piping is an important part of agricultural engineering and water conservancy projects, which plays an important role in solving the uneven space-time distribution of water resources. The vibration during the operation is the critical problem in the design and safety evaluation of water pipeline. In order to solve the problem of how to improve the precision of the FSI (fluid-solid interaction) model in the natural vibration characteristics analysis of the piping, two different FSI models of a piping in cascade pumping station of Jingdian Project were built, by using the additional mass method and direct coupling method respectively. Then the modal characteristics of two FSI models which were obtained in the natural vibration characteristics analysis were compared with the modal characteristics of the prototype piping identified by stochastic subspace identification (SSI) method. The comparison results show that the simulation results of the model by using direct coupling method were in good agreement with the results identified by SSI method, and the maximum error was 3.62%. In the comparison of calculation accuracy of the same order, the model by using direct coupling method outperforms the model by using additional mass method, making up for the lack of the modes that the additional mass model can not work out. The results show that FSI affects the piping system modal frequency seriously and the model by using direct coupling method is superior to the additional mass model in terms of the order number and precision of the simulation, reflecting the real natural vibration characteristics of liquid conveying piping. This method can be used in the analysis of the dynamic characteristics of complicated pipe systems.

cascade pumping station; pipe; vibration characteristics; additional mass method; direct coupled method; modal parameter identification

10.6041/j.issn.1000-1298.2017.03.017

2016-07-14

2016-08-31

國家自然科學基金項目(51679091)和河南省高等學校青年骨干教師資助計劃項目(2012GGJS-101)

張建偉(1979—)，男，副教授，博士，主要從事水利水電工程研究，E-mail： zjwcivil@126.com

TV31

A

1000-1298(2017)03-0134-07