路網中位置不確定的二元反kNN查詢
徐 偉,李文根,張毅超,關佶紅
(同濟大學 計算機科學與技術系,上海 201804)
(*通信作者電子郵箱jhguan@tongji.edu.cn)
路網中位置不確定的二元反kNN查詢
徐 偉,李文根,張毅超,關佶紅*
(同濟大學 計算機科學與技術系,上海 201804)
(*通信作者電子郵箱jhguan@tongji.edu.cn)
針對路網限制和物體位置的不確定性,提出了路網中位置不確定的二元反kNN查詢(PBRkNN),旨在查找一組位置不確定的點,使得每個不確定點的kNN包含給定查詢點的概率大于一個閾值。為了解決該問題,首先提出一種基于Dijkstra進行剪枝處理的基本算法,即PE算法;接著在PE算法的基礎上通過預處理計算出每個點的kNN從而加快查詢速度,即PPE算法;而為了進一步減小PPE算法中范圍查詢的開銷,提出PPEE算法,利用網格索引來索引范圍查詢中要查詢的不確定空間點,從而提升算法的效率。最后,在北京和加州路網數據集上進行了大量實驗,結果表明通過一些預處理的策略確實可以有效地處理路網中位置不確定的二元反kNN查詢。
反kNN查詢;路網;Dijkstra算法;不確定性
0 引言
隨著空間定位技術和移動通信技術的發展,以及手機等智能設備的廣泛使用,各種基于位置的服務(Location Based Service, LBS)得到了越來越廣泛的應用。作為基于位置應用中重要的查詢之一,反kNN查詢(即尋找查詢點是哪些點的k最近鄰(k-Nearest Neighbor,kNN))[1]在現實生活中被廣泛用于諸如決策系統[1]、超市的選址、出租車的調度[2]和龍卷風預測[2]等領域。
已有的關于反kNN查詢的研究主要分為三類:基于歐氏距離的反kNN查詢[1,3-6]、基于路網距離的反kNN查詢[7-10]和不確定反kNN查詢[2,11-15]。不確定性的引入主要由于物體位置更新的時間間隔、網絡傳輸延遲、數據隱私保護和定位設備的誤差等因素會導致物體位置存在必然的不確定性。目前,不確定反kNN研究主要集中在歐氏空間。考慮到物體的移動受限于實際的路網,有必要進行路網中不確定性的反kNN查詢研究。
反kNN查詢可以分為兩類:一元反kNN查詢和二元反kNN查詢。其中一元反kNN查詢中的候選集合只有一種類型,查詢目標是計算查詢點是候選集中哪些點的kNN;二元反kNN查詢的查詢集合則分為兩類A和B,查詢點與其中一個候選集A類型相同,查詢目標是計算查詢點是候選集B中哪些元素的kNN,值得注意的是,對于B中每個元素的kNN是指A中離其最近的k個元素。二元反kNN查詢在實際生活中有著廣泛的應用,特別是結合路網和位置不確定性的二元反kNN更加符合現實生活。如在出租車的派單系統中,對于每個乘客的訂單派送選擇就可以看成是以乘客為查詢點的反kNN查詢;另外因為出租車一直運動,實時位置必然存在一定的不確定性。本文結合路網和位置的不確定性,旨在研究路網中位置不確定的二元反kNN查詢處理。
下面從歐氏空間中的反kNN查詢、路網中的反kNN查詢和不確定的反kNN查詢這三個方面介紹反kNN查詢的研究現狀。
1)歐氏空間中的反kNN查詢。現有的基于歐氏空間的反kNN查詢的算法主要分為三步:1)建立索引;2)在已構建好的索引結構的基礎上通過一些剪枝過濾策略,剪掉一些不可能的空間點;3)對剩下的候選點進行驗證,得到最終滿足條件的結果。具體地,索引主要有R樹、R+-樹和R*樹;剪枝策略則主要分為基于自身限制的剪枝[1,3]和基于其他元素限制的剪枝[4-6];候選點的驗證主要采用kNN查詢或者range-k查詢。但是這類查詢沒有考慮移動物體位置的不確定性。
2)路網中的反kNN查詢。Yiu等[7]第一次提出了基于路網的反kNN查詢,其處理流程與歐氏空間中的反kNN類似。不過,針對路網中的反kNN查詢的特點,索引方面主要采用泰森多邊形(Voronoi圖)[8]和鄰接表[9-10];剪枝則根據更近鄰原則[8]實現;驗證同樣使用kNN查詢。這類查詢雖然將反kNN查詢引入到路網中,但是沒有考慮到路網中移動物體的不確定性問題。
3)不確定的反kNN查詢。Lian等[11]第一次提出了基于位置不確定性的反kNN查詢。這類問題的主要難點在于位置不確定性的表示和基于這種表示的高效索引與剪枝。這類問題主要分為四步:1)不確定性的表示,主要有最小邊界圓[11]和最小邊界矩形[2,11-15];2)基于空間位置的剪枝,即不考慮它們的概率分布,主要是基于半分策略[12-14];3)基于概率的剪枝,主要是劃分圓[2,15];4)驗證采用kNN查詢。這類查詢雖然引入了移動物體位置的不確定性,但是并沒有考慮路網中位置不確定性的反kNN查詢。
綜上所述,已有的反kNN查詢算法沒有同時考慮路網限制和物體位置的不確定性,不能直接用于解決本文所提出的路網中位置不確定的反kNN查詢問題。
1 問題定義
首先給出路網和空間點的定義。
定義1 路網(Road Network)。路網本質上一個圖G=〈V,E〉。其中:V代表節點的集合,表示路網中道路的拐點或交叉點;E是邊的集合,每條邊連接兩個節點。
定義2 空間點(PointOnNetwork,PON)。一個空間點表示為p=〈e,pos〉。其中:e表示空間點所在的邊,pos表示空間點p到e的開始端的偏移。
在定義不確定空間點(UncertainPON,UPON)之前,先描述不確定空間點的表現形式。在歐氏空間中,物體的不確定位置表示為一個橢圓或多邊形。如圖1,物體在a處的不確定表示就是圍繞a點的橢圓。然而,在路網中,物體運動受限于路網。例如,圖1存在著實際路網bd和ce,歐氏空間中陰影的范圍在路網中的不確定性表示就是4個路段即ab、ac、ad和ae。因此,在路網中UPON位置由多個路段來表示。把組成不確定空間點的路段稱為不確定路段(UncertainSegment)。下面給出不確定路段和不確定空間點的定義。
定義3 不確定路段。不確定路段表示為us=〈edge,fromPos,toPos〉。其中:edge表示該不確定路段所在的邊,fromPos和toPos分別表示該確定性路段首尾位置。
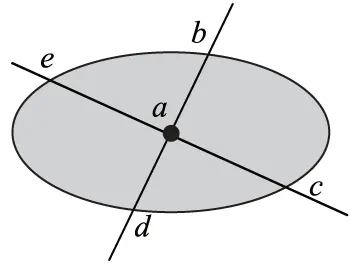
圖1 不確定區域
定義4 不確定空間點。一個不確定空間點表示為up=〈us0,us1,…,usm-1〉,其中usi表示物體可能出現不確定路段。
定義5 不確定空間點的范圍長度ul(UPONlength)。一個不確定空間點up=〈us0,us1,…,usm-1〉的范圍長度ul為:
ul(up)=∑len(usi)
(1)
其中len(usi)=toPosi-fromPosi。
下面給出路網中位置不確定的二元反kNN查詢的定義。
定義6 路網中位置不確定的二元反kNN查詢(Probabilistic Bichromatic Reverse-kNN query on road network, PBR-kNN)。給定路網G,空間點PON集合A={p0,p1,…,pn-1},不確定空間點UPON集合B={up0,up1,…,upm-1},一個概率閾值? 和一個查詢點q∈A,PBR-kNN查詢的目標是查找B的一個子集Bp,滿足:
Bp={up|P(q∈PkNN(up))≥?,up∈B}
(2)
其中P(q∈PkNN(up))表示q為up的kNN概率,即:
(3)
其中,{p|q∈kNN(p),p∈up}得到的點集合剛好可以組成若干個連續的路段。在PBR-kNN查詢中,集合A中的元素與查詢點q是競爭關系,所以A的元素與q一樣為PON。
2 PE算法
為了有效解決路網中位置不確定的二元反kNN查詢,首先設計了Probabilistic Eager(PE)算法,作為解決此問題的一個基本方法。PE算法的思想是基于Dijkstra算法加剪枝。
2.1 索引結構
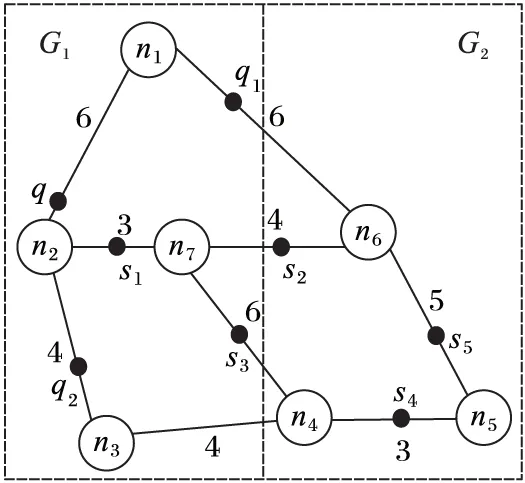
為了節省空間,便于每條邊上的PON和UPON的索引,PE算法采取類鄰接表的方法存儲路網。在鄰接表中每個節點都會有個鄰接節點表,本文采用另外獨立索引每條邊的方式將鄰接節點表變成鄰接邊表。如圖2所示路網建立索引,其中:q1和q2為興趣點,q為查詢點,s1n7、s2n7、s3n7組成up1,s4n5、s5n5組成up2,q1n1=2,q2n2=3,qn2=2,s1n7=1,s2n7=2,s3n7=3,s4n5=1,s5n5=2。假設邊n1n2、n1n6、n2n4和n2n7的ID分別為e1、e2、e3和e4,則n1、n2的鄰接表如圖3。
PE算法給每條邊編一個ID,每條邊會記錄這條邊兩端節點的編號。對于每條邊上的空間點,會有一個PONlist表按照距離邊起始端的距離排序。對于每條邊上的不確定路段,會有一個UncertainList表記錄在這個邊上出現過的不確定空間點。對于不確定空間點,用一個單獨的鏈表來索引每個不確定空間點的路段。圖2的索引結果如圖4所示。
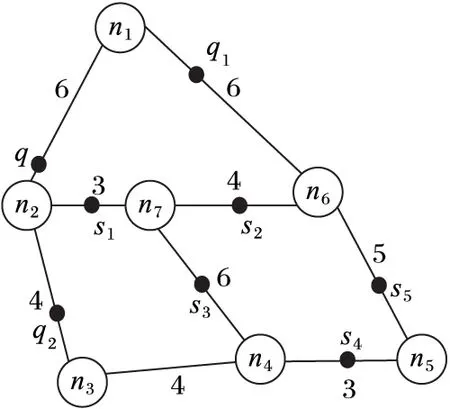
圖2 一個路網的例子
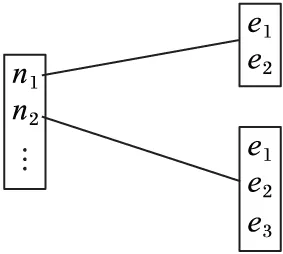
圖3 路網索引
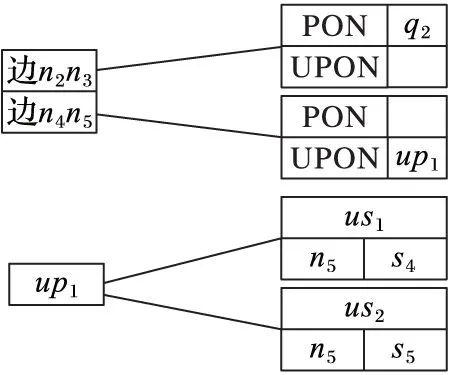
圖4 邊及不確定空間點索引
2.2 查詢算法
引理1 對于不確定路段us(edge〈n1,n2,length〉,fromPos,toPos)和查詢點q,如果n1?BRkNN(q),n2?BRkNN(q),則有:
P(us∈BRkNN(q))=0
(4)
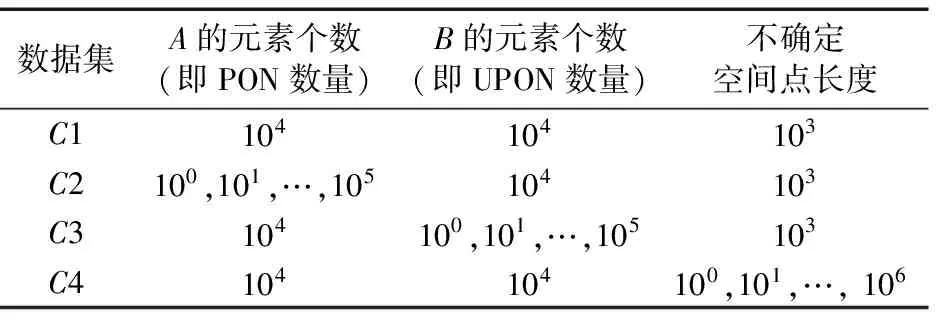
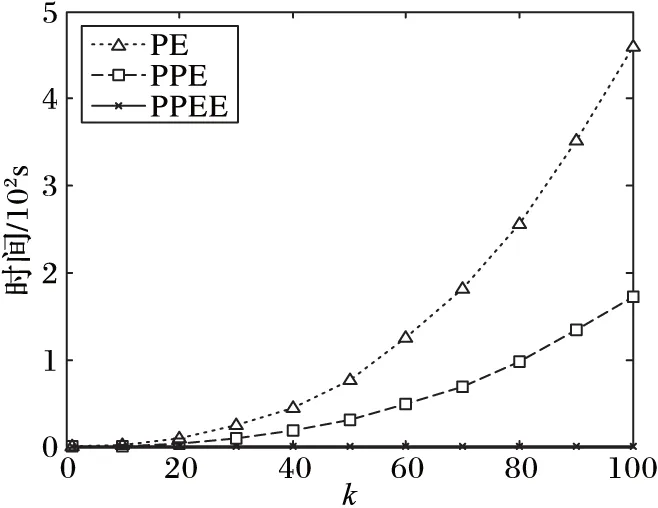
引理2 對于一條邊(edge〈n1,n2,length〉),所有滿足{p|q∈BRkNN(p),p∈edge}條件的PON構成的區域剛好是整個edge的所有范圍或者兩個分開的路段s1〈edge,fromPos1,toPos1〉,s2〈edge,fromPos2,toPos2〉滿足fromPos1=0,toPos2=length,并且toPos1 證明 反證法:假設存在一個路段s〈edge,fromPos,toPos〉包含所有滿足條件的PON點,且fromPos不等于0,toPos不等于length。假設d(q,n1) dist(p,p1)=min(dist(p,n1)+dist(n1,p1), dist(p,n2)+dist(n2,p1)) 情況一dist(p,p1)=dist(p,n1)+dist(n1,p1)。 dist(p,n1)+dist(n1,p1) dist(p,n1)=dist(p,p1)-dist(n1,p1)> dist(q,p1)-dist(n1,p1)=dist(q,n1) 所以n1也是滿足條件的點,與fromPos=0矛盾。 情況二dist(p,p1)=dist(p,n2)+dist(n2,p1)。 dist(p,n1)+dist(n1,p1)>dist(p,n2)+dist(n2,p1) dist(p,n1)>dist(p,p1)-dist(n1,p1)> dist(q,p1)-dist(n1,p1)=dist(q,n1) 所以n1也是滿足條件的點,與fromPos=0矛盾。 綜上所述,不存在這樣的路段s,所以問題得證。 推理1q為查詢點,n為路網節點,由文獻[7]中引理1和本文中引理1可以得到,如果存在k個空間點p0,p1,…,pk-1滿足d(n,pi) P(us∈BRkNN(q))=0 (5) 證明 因為n1和n2到q點的最短路徑都要經過n,由文獻[7]中引理1得n1?BRkNN(q),n2?BRkNN(q),由本文中的引理1得P(us∈BRkNN(q))=0。 PE算法的基本邏輯其實非常簡單,就是不停地在集合B中尋找可能是結果的upi,然后判斷P(q∈PkNN(upi))的值是否大于?。 1)尋找可能的upi。 最簡單的辦法就是根據距離q點的距離,由近及遠進行遍歷作為候選者upi,那么就可以使用Dijkstra算法進行擴展。但是由推理1,可以從節點n處剪枝掉很多不可能的節點,提高尋找候選者的效率。所以算法的主要流程如下: 1)初始化一個小頂堆。 2)將查詢點q〈edge,pos〉所在邊的兩個端點加入堆中,即〈n1,pos〉和〈n2,edge.length-pos〉。 3)驗證edge上是否有符合條件的不確定性路段。 4)基于Dijkstra算法對路網進行擴展,對符合推理1的節點進行剪枝。 假設訪問到了節點n: a)計算n的kNN(n)={p1,p2,…,pk}; b)對于pi驗證在range(n,q)范圍內的邊上是否有滿足條件的us(實際上是再次計算pi的kNN)。 c)如果q?kNN(n),根據推理1剪掉節點n,否則將n的鄰接節點加入到堆中。 說明:PE算法以不確定性路段作為最基本的單位分開計算每個路段成為q的RkNN的概率,一個不確定性空間點的所有不確定性路網都計算完,或者程序結束前,就會計算每個被訪問過的不確定空間點成為q的RkNN的概率,并篩選出概率值大于設定的概率閾值的。 2)驗證候選者upi。 如前面所說,對于候選者upi的驗證,先計算組成upi的usi0,usi1,…,usi(m-1)的概率,然后再驗證upi是否滿足要求。對于路網的同一條邊上可能會有多個us,而對于每個us的驗證都與該邊的兩個端點有關,所以對于同一條邊上的us,它們的驗證計算可能差不多。為了提高計算效率,PE算法先計算出us所在的邊edge上哪些區域段中的點是滿足為q點RkNN的,即 UAR={us|?p∈us,q∈BRkNN(p),us∈edge} 然后再計算usij中有多少包含在集合UAR中。假設計算的邊為edge〈n1,n2,len〉,計算UAR的算法主要包括以下步驟:計算kNN(n1)和kNN(n2);如果q不在kNN(n1)和kNN(n2)中,則返回空;根據引理2,UAR分成從n1起始的路段us1和從n2起始的路段us2計算;驗證us1和us2是否要合并,并返回結果。 3.1 PPE算法 PE算法包含大量兩個路網節點間的最短距離計算,而在路網上計算兩點距離的算法比歐氏空間中的距離計算復雜很多。為了提高PE算法的效率,采用文獻[7]的方法提前算出每個節點的kNN(這里的kNN是指k最近鄰的PON點),稱之為Pre-compute Probabilistic Eager (PPE)算法。這樣,PE算法中尋找可能upi的第4.a)步和驗證候選者upi的第4.b)步,每次計算節點的kNN就可以省去,能極大地提高算法效率。 在預處理中,k設為可能取到的最大值。在實際生活中,k一般取到20就可以了。為了實驗需求,本文k取100。 3.2 PPEE算法 在尋找候選upi的過程中,第4)步中的a)、b)可以同時計算,但是經過PPE算法的改進,b)還需要重新獨立地計算才能得到候選者。為此提出基于網格劃分索引的策略,從快速計算出候選者的角度來進一步提高查詢的效率,稱為Pre-computeProbabilisticEagerExternal(PPEE)算法。 3.2.1 數據索引 1)網格劃分。PPEE算法按照物體點的平面坐標劃分網格,這樣可以方便數據的管理和查詢,便于數據的網格定位和快速找到每個網格四周的網格。對于一個不確定性路段可能出現在多個網格中的情況,PPEE算法采取多冗余化簡便的辦法,在包含該不確定性路段的所有網格中都添加該不確定性路段。如圖5是圖2路網的一個網格劃分。 圖5 網格劃分 2)不確定性路段索引。因為一條邊上可能會出現多個不確定性路段,而且在處理不確定性路段時,同一條邊上的多個不確定性路段同時處理效率會更高,所以PPEE算法對不確定性路段的索引是對含有不確定性路段的邊進行索引。這樣既可以減小檢索塊的尺寸又可以提高索引查找的效率。使用圖5的劃分規則,得到的索引如圖6。 3)不確定性索引的更新。由于不確定性索引的更新可能會很快也可能很慢,為此PPEE算法采取類似于內存管理的策略。針對每一條邊,不確定性路段的更新包括以下四種情況: 1)該邊上增加了新的不確定性路段,但增加之前該邊上已有不確定性路段; 2)該邊上增加了新的不確定性路段,但是增加之前該邊上沒有不確定性路段; 3)該邊上減少了不確定性路段,但是減少之后該邊上還有不確定性路段; 4)該邊上減少了不確定性路段,減少之后該邊上就不存在不確定性路段了。 對于情況1)和3),索引不需要作任何改變;對于情況2),則需要把該邊添加到該邊所在網格的索引表中;對于情況4),本來應該從該邊所在網格的索引表中把該邊刪除,但是考慮到接下來可能還會有不確定性路段更新,因而采取延遲更新的策略,即在后來的查詢算法中查找到該邊時,如果該邊上沒有不確定性路段,就把它從索引表中刪除。 圖6 不確定性的索引 3.2.2 查詢算法 PPEE算法在PPE算法的基礎上對不確定性空間點作索引,它們的不同之處在于尋找候選不確定空間點集合。基于網格索引的尋找候選不確定空間點的算法如下: 輸入 節點n; 輸出 候選不確定空間點。 1)令d為kNN(n)中距離n點最遠的距離。 2)定位n所在的網格為gridn。 3)計算到gridn的四邊的距離小于等于d的所有網格集合Grids。 4)遍歷Grids中所有的grid。對于gridi,遍歷gridi索引中的每條邊edgei中索引的不確定路段作為候選者。對于edgei如果不包含不確定路段,則從索引表中刪除。 在PPEE算法中,每條邊和每個劃分網格都會記錄是否被訪問過,以防止重復訪問。 4.1 實驗數據 實驗采用北京和加州的路網,其中北京路網的節點和邊的數目分別為84 084和104 313;加州路網的節點和邊的數目分別為21 048和21 693。 1)北京路網PON和UPON生成:實驗采用北京出租車數據,包含11 716輛出租車2012年某個月的采樣數據。將給定時刻叫車的乘客作為PON空間點集合,此時刻的空出租車則作為UPON集合。生成規則如下:選取一個打車比較多的時間點t,如果出租車在t時刻前后30min內有載新乘客的動作,說明這個點有一個乘客,則將其加入到A集合;如果在這個時間點前后兩個采樣點都是空車的狀態,那就生成一個UPON,UPON的中心點就是距t最近的采樣點的位置,范圍為這兩個采樣點的距離。生成好之后就可以加入到UPON集合中。最終生成的空間點集合A共866個元素,不確定性區域集合B共3 994個元素,不確定性路段數為785 125。 2)加州路網上的PON和UPON生成:以加州路網為基礎,運用隨機函數根據一定的限制生成,生成方法則模擬前面北京路網真實數據的生成。首先,按照集合A要求的元素個數,對集合A中每個點p〈edge,pos〉,按照edgeId和pos隨機生成。然后,按照集合B要求的元素個數,先按照生成集合A的辦法,生成|B|個點p0,p1,…,p|B|-1;接著,按照平均不確定性長度ul,生成|B|個長度值ul0,ul1,…,ul|B|-1,使得它們的平均值為ul;最后,以pi為中心,不確定性長度為uli,按照前面真實數據的生成方法生成upi。該實驗數據集如表1所示。 表1 實驗數據集 實驗參數設置如表2所示。 表2 實驗參數設置 實驗運行于配置為IntelCorei7- 4790KCPU@ 4.00GHz16GBRAM的計算機,采用Java環境。實驗結果為100次實驗的平均值。 4.2 實驗結果分析 1)k值大小對算法查詢時間的影響:本組實驗分別在兩個數據集上進行。從圖7、8可以看出,當k較小時,三個算法的時間開銷差異很小。隨著k的增加,三種算法的時間開銷均在增加,PE算法進行的range查詢按照訪問節點的平方數增長,而PPE算法是線性增長的,所以這兩條線中PE算法曲線變化比PPE算法更明顯;而PPEE算法進行range查詢的花費為0,但隨著k的增加,訪問的grid數也隨訪問的節點數線性增長,而訪問grid的花費明顯比range查詢少很多,所以PPEE算法的曲線變化更小。在實際的生活中,k可能只會取到40,由圖7可以看出,在k<40時,最快的查詢算法即PPEE算法可以在100ms之內計算出結果。 2)PON數量對算法查詢時間的影響:本組實驗使用加州路網的數據集C2。由圖9可以看出,在PON數量(即集合A中元素的個數)比較小時,PON分布比較稀疏,這樣利用推理1進行剪枝的效果會比較差,仍然需要進行多次range查詢,所以PE算法和PPE算法的效果在A的個數小于100時并不明顯;但對于PPEE算法,因為不需要進行range查詢,所以影響不大。 3)UPON數量對算法查詢時間的影響:本組實驗使用加州路網的數據集C3。三種算法遍歷的路網節點的個數沒有變化,變化的只是需要驗證的邊的個數。由圖10可以看出,在UPON的數量(即集合B元素中元素的個數)大于10 000時,PPEE算法的花費明顯大于PPE,這是因為隨著B中元素個數的增加,PPEE算法需要驗證的UPON數量增長的速度比算法PE和PPE快很多。 注意:在圖9~11中為了更好地展示結果,橫軸都采用指數的形式來表示。 4)不確定路段范圍長度對查詢時間的影響:本組實驗使用加州路網的數據集C4。集合B中UPON平均長度的增加不會顯著影響三個算法訪問的節點個數,但是會增加待驗證的邊上不確定性路段的個數。從圖11可以看出,當平均區域長度大于100 000時,PPEE算法的時間曲線變化非常明顯,查詢時間比PE和PPE更長,這是因為PPEE算法采用劃分網格的策略尋找那些需要驗證的不確定性路段,這樣使得需要驗證的數量比另外兩種算法大幅增加。 圖7 北京路網數據集查詢時間與k的關系 圖8 加州路網數據集查詢時間與k的關系 圖9 集合A的個數與查詢時間的關系 圖10 集合B的個數與查詢時間的關系 圖11 UPON平均長度與查詢時間的關系 本文結合路網和物體位置的不確定性研究了路網中位置不確定的二元反kNN查詢問題。為了解決該問題,首先針對路網中位置不確定性提出了一個表示模型,并在此基礎上提出了一個基本的查詢處理算法即PE算法;在PE算法的基礎上,又進一步提出了兩種改進的處理算法,即PPE算法和PPEE算法。實驗結果表明,PE算法適合處理k值較小的查詢,因為它的時間開銷隨著k的增加呈現指數增長;PPE算法的時間開銷則隨著k的增加線性增長,適合處理具有較大k值的查詢;PPEE算法性能最好,隨著k的增加,它的時間開銷增長非常緩慢,算法總的處理時間小于100 ms,能夠很好地滿足實時查詢的要求。 References) [1] KORN F, MUTHUKRISHNAN S.Influence sets based on reverse nearest neighbor queries[J].ACM Sigmod Record, 2000, 29(2): 201-212. [2] NIEDERMAYER J, ZüFLE A, EMRICH T, et al.Probabilistic nearest neighbor queries on uncertain moving object trajectories [J].Proceedings of the VLDB Endowment, 2013, 7(3): 205-216. [3] LU J, LU Y, CONG G.Reverse spatial and textualknearest neighbor search [C]// SIGMOD 2011: Proceedings of the 2011 ACM SIGMOD International Conference on Management of Data.New York: ACM, 2011: 349-360. [4] YANG S, CHEEMA M A, LIN X, et al.SLICE: reviving regions-based pruning for reverseknearest neighbors queries [C]// ICDE 2014: Proceedings of the 2014 IEEE 30th International Conference on Data Engineering.Washington, DC: IEEE Computer Society, 2014: 760-771. [5] WU W, YANG F, CHAN C-Y, et al.FINCH: evaluating reversek-nearest-neighbor queries on location data [J].Proceedings of the VLDB Endowment, 2008, 1(1): 1056-1067. [6] CHEEMA M A, LIN X, ZHANG W, et al.Influence zone: Efficiently processing reverseknearest neighbors queries [C]// Proceedings of the 2011 IEEE 27th International Conference on Data Engineering.Washington, DC: IEEE Computer Society, 2011: 577-588. [7] YIU M L, PAPADIAS D, MAMOULIS N, et al.Reverse nearest neighbors in large graphs [J].IEEE Transactions on Knowledge & Data Engineering, 2006, 18(4): 540-553. [8] SAFAR M, IBRAHIMI D, TANIAR D.Voronoi-based reverse nearest neighbor query processing on spatial networks [J].Multimedia Systems, 2009, 15(15): 295-308. [9] BORUTTA F, NASCIMENTO M A, NIEDERMAYER J, et al.Monochromatic RkNN queries in time-dependent road networks [C]// MobiGIS ’14: Proceedings of the 2014 ACM SIGSPATIAL International Workshop.New York: ACM, 2014: 26-33. [10] GAO Y, QIN X, ZHENG B, et al.Efficient reverse top-k boolean spatial keyword queries on road networks [J].IEEE Transactions on Knowledge & Data Engineering, 2015, 27(5):1205-1218. [11] LIAN X, CHEN L.Efficient processing of probabilistic reverse nearest neighbor queries over uncertain data [J].The VLDB Journal, 2009, 18(3): 787-808. [12] BERNECKER T, EMRICH T, KRIEGEL H-P, et al.Efficient probabilistic reverse nearest neighbor query processing on uncertain data [J].Proceedings of the VLDB Endowment, 2011, 4(10): 669-680. [13] YU G, GU Y, QIAO J, et al.Interval reverse nearest neighbor queries on uncertain data with Markov correlations [C]// ICDE ’13: Proceedings of the 2013 IEEE International Conference on Data Engineering.Washington, DC: IEEE Computer Society, 2013: 170-181. [14] EMRICH T, KRIEGEL H-P, MAMOULIS N, et al.Reverse-nearest neighbor queries on uncertain moving object trajectories [M]// DASFAA 2014: Proceedings of the 19th International Conference on Database Systems for Advanced Applications, LNCS 8422.Berlin: Springer-Verlag, 2014: 92-107. [15] JAMPANI R, XU F, WU M, et al.MCDB: a Monte Carlo approach to managing uncertain data[C]// SIGMOD ’08: Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data.New York: ACM, 2008: 687-700. This work is partially supported by the National Natural Science Foundation of China (61373036), the Program of Shanghai Subject Chief Scientist (15XD1503600). XU Wei, born in 1991, M.S.candidate.His research interests include spatial keyword query, data mining, LI Wengen, born in 1987, Ph.D.candidate.His research interests include spatial database, data mining. ZHANG Yichao, born in 1982, Ph.D., assistant professor.His research interests include complex network, data mining. GUAN Jihong, born in 1969, Ph.D., professor.Her research interests include spatial database, data mining. Probabilistic bichromatic reverse-kNN query on road network XU Wei, LI Wengen, ZHANG Yichao, GUAN Jihong* (DepartmentofComputerScienceandTechnology,TongjiUniversity,Shanghai201804,China) Considering the road network constraint and the uncertainty of moving object location, a new reverse-kNN query on road network termed Probabilistic Bichromatic Reverse-kNN (PBRkNN) was proposed to find a set of uncertain points and make the probability which thekNN of each uncertain point contains the given query point be greater than a specified threshold.Firstly, a basic algorithm called Probabilistic Eager (PE) was proposed, which used Dijkstra algorithm for pruning.Then, the Pre-compute Probabilistic Eager (PPE) algorithm which pre-computes thekNN for each point was proposed to improve the query efficiency.In addition, for further improving the query efficiency, the Pre-compute Probabilistic Eager External (PPEE) algorithm which used grid index to accelerate range query was proposed.The experimental results on the road networks of Beijing and California show that the proposed pre-computation strategies can help to efficiently process probabilistic bichromatic reverse-kNN queries on road networks. reverse-kNN query; road network; Dijkstra algorithm; uncertainty 2016- 08- 12; 2016- 09- 13。 國家自然科學基金資助項目(61373036);上海市優秀學術帶頭人計劃項目(15XD1503600)。 徐偉(1991—),男,江蘇淮安人,碩士研究生,CCF會員,主要研究方向:空間關鍵詞查詢、數據挖掘; 李文根(1987—),男,四川南充人,博士研究生,CCF會員,主要研究方向:空間數據庫、數據挖掘; 張毅超(1982—),男,上海人,助理教授,博士,CCF會員,主要研究方向:復雜網絡、數據挖掘; 關佶紅(1969—),女,遼寧開原人,教授,博士生導師,博士,CCF高級會員,主要研究方向:空間數據庫、數據挖掘。 1001- 9081(2017)02- 0341- 06 10.11772/j.issn.1001- 9081.2017.02.0341 TP311.13; TP392 A3 PPE算法和PPEE算法
4 實驗結果與分析

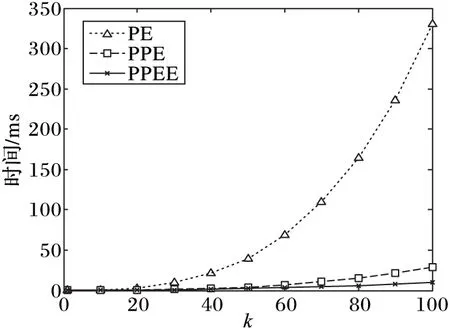

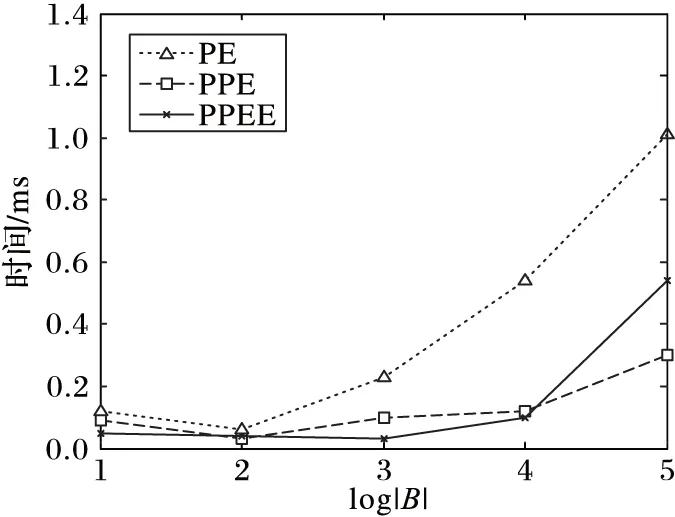
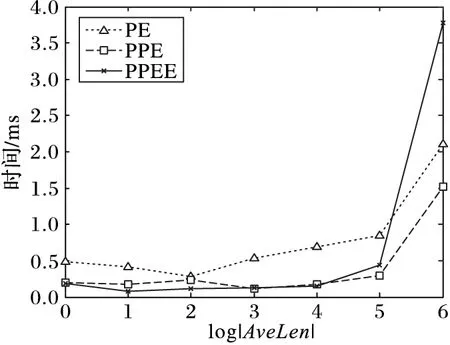
5 結語

