考慮軋制界面粗糙形貌的軋機輥系非線性振動特性研究

孫韻韻， 肖會芳， 徐金梧

(北京科技大學 鋼鐵共性技術協同創新中心，北京 100083)

考慮軋制界面粗糙形貌的軋機輥系非線性振動特性研究

孫韻韻， 肖會芳， 徐金梧

(北京科技大學 鋼鐵共性技術協同創新中心，北京 100083)

軋制界面的粗糙形貌可導致界面行為的根本變化，極大地影響著軋機輥系的動力學響應行為。考慮軋制界面粗糙形貌的影響，建立了軋機輥系系統的非線性垂直振動動力學模型，計算了具有不同粗糙形貌軋制界面的軋機輥系系統非線性剛度特性和固有頻率特性，并與采用Duffing振子描述界面剛度的傳統軋機模型進行了對比。采用多尺度法求解了考慮界面粗糙形貌影響的軋機系統主共振幅頻特性方程，并推導了系統受迫振動響應的跳躍頻率和跳躍幅值表達式，分析了軋制界面粗糙形貌、激勵載荷、非線性剛度率和阻尼對軋機輥系系統動力學響應特性的影響，為抑制軋機振動提供有效的理論參考。

軋機；垂直振動；粗糙形貌；非線性

高速軋機普遍存在振動，軋機振動不僅直接影響帶鋼產品表面質量，降低產品的成材率，嚴重時甚至引發軋機的顫振，導致斷帶等生產事故[1]。軋輥與帶鋼形成的軋制界面作為軋制過程的工作界面，其動力學特性對軋機振動有決定性影響。

近年來，許多學者將軋制界面特性與軋機振動之間的機理關系作為研究的重點。YOUNES等[2]將軋件等效為具有線性剛度的彈性零件，建立了軋機系統線性垂直振動模型。由于在高速軋制過程中，軋制界面接觸剛度、阻尼的非線性特征客觀存在，簡化的線性接觸剛度和阻尼模型難以真實準確地描述軋制界面的非線性動力學特征[3-6]。JOHNSON等[7]在軋制顫振模型中首次考慮了工作輥-支承輥界面的接觸非線性因素對動力學特性的影響，指出非線性可以產生高頻諧波振動。軋制時輥縫內高壓、高溫、高速的惡劣工作條件極易引起軋輥表面磨損而產生凹坑、麻點等缺陷，導致軋制界面有不同程度的粗糙形貌，軋制界面粗糙形貌特征的變化可使軋機系統動力學特性變化。目前，軋制界面的非線性剛度特性通常采用Duffing振子模型進行描述[8-9]。但是基于Duffing振子非線性剛度特性建立的軋機系統動力學模型，沒有考慮軋制界面粗糙形貌等小尺度特征參數對界面動力學行為的影響，尚不能準確地描述軋機系統動力學特性。

本文考慮無潤滑軋制界面粗糙形貌的影響，建立了軋機輥系非線性垂直振動動力學模型，計算了具有不同粗糙形貌軋制界面的軋機輥系系統的非線性剛度特性和固有頻率特性，并與采用Duffing振子描述界面剛度的傳統軋機模型進行對比。采用多尺度法求解了軋機輥系幅頻響應特性方程，并計算跳躍頻率和幅值，分析了軋制界面粗糙形貌和系統參數對軋機輥系主共振幅頻曲線的影響特性，為改善板帶表面質量，抑制軋機垂直振動提供基礎。

1 考慮軋制界面粗糙形貌的軋機輥系非線性動力學模型

1.1 動力學模型描述

軋機輥系主要由機架、工作輥、支撐輥和軋件等組成，將工作輥和支撐輥簡化為一個集中質量塊m，建立的軋機輥系垂直振動動力學模型，如圖1所示。其中，c1和k1分別為輥系與機架間的等效線性阻尼和剛度，vr為軋輥轉速，r為軋輥半徑。軋制過程中，由于板厚變化、張力波動等因素的影響，軋輥受到周期性外部擾動Ecos(ωt)。其中，E為簡諧外激勵幅值，ω為外激勵角頻率。

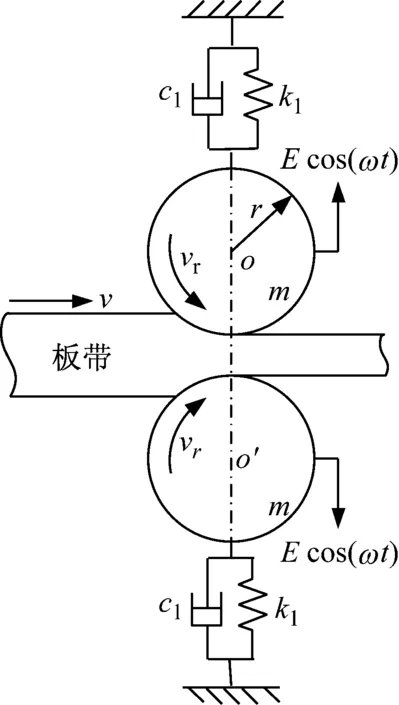
圖1 軋機系統垂直振動示意圖

由于軋機輥系上、下結構具有基本對稱性且輥系垂直方向的振動中出現較多的是對稱振動形式，因此，其動力學模型可以采用上軋輥-軋制界面或下軋輥-軋制界面進行描述[10-11]。本文以上軋輥-軋制界面為研究對象，將軋制過程中軋輥與軋件的相互作用等效為彈性體與剛性平面間的接觸振動，考慮軋制界面粗糙形貌對接觸剛度的影響，并假設軋制界面阻尼為線性粘彈性模型[11-14]，建立的軋機輥系非線性動力學模型，如圖2所示。其中，坐標原點為軋輥處于靜平衡位置，c2為軋制界面等效線性阻尼，zs為系統處于平衡位置時彈簧的變形量，z為軋機輥系相對于靜平衡位置的位移。

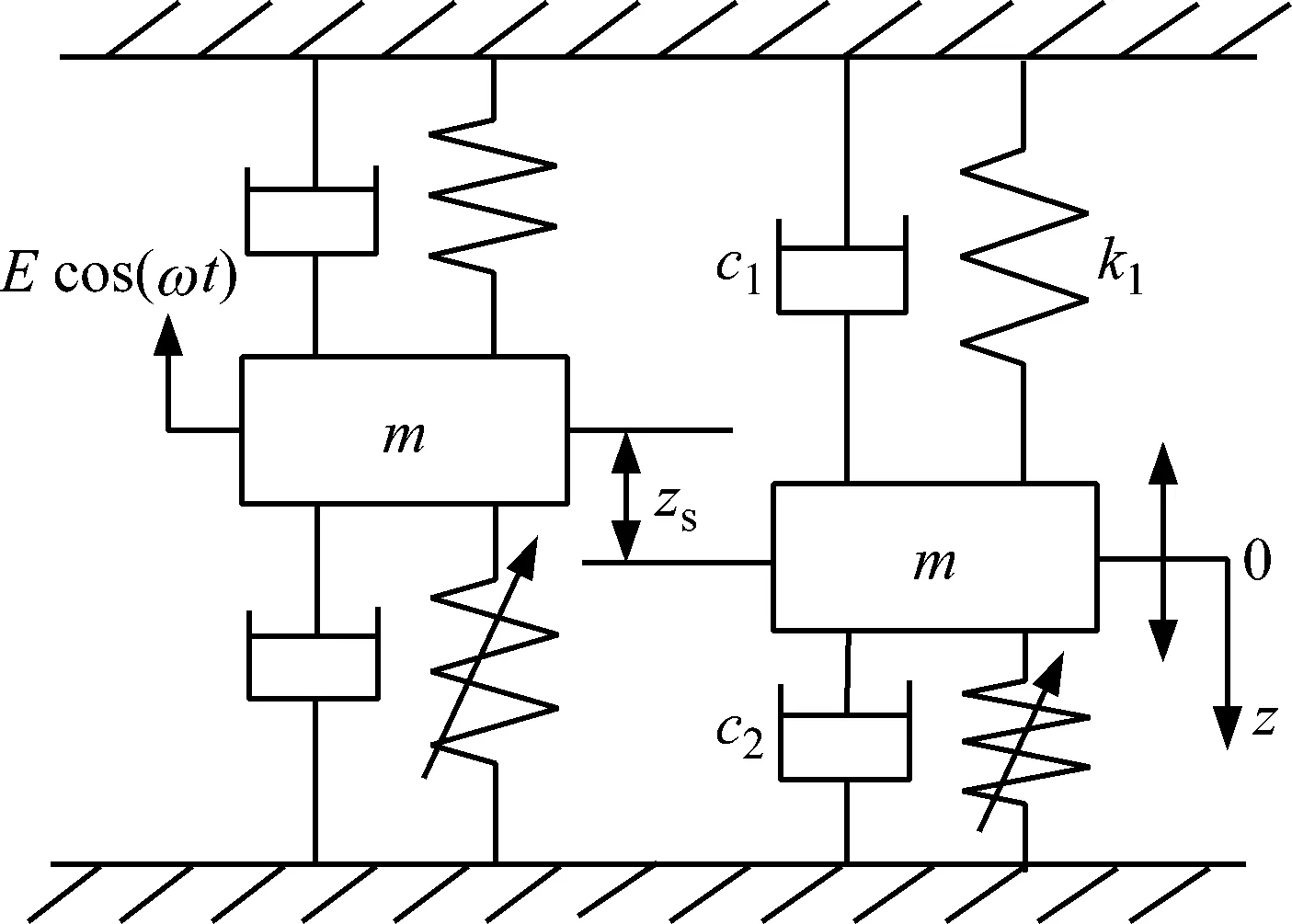
圖2 軋機系統非線性動力學模型

圖2所示的考慮軋制界面粗糙形貌的軋機輥系非線性動力學模型，在其靜平衡位置附近的垂直振動動力學方程可以表示為

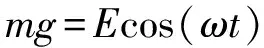
(1)

其中，fn(z,zs)表示粗糙軋制界面的非線性彈性回復力。

1.2 粗糙界面非線性彈性回復力

為了獲得軋機輥系的動力學響應特性，需要首先確定粗糙軋制界面的非線性彈性回復力fn(z,zs)。通常，軋制界面的粗糙形貌可以采用統計學參數進行表征和描述，如表面高度的標準偏差Rq、傾斜度Sk和峭度K，但是這些統計學參數依賴于樣本的尺寸和測試儀器精度，具有尺度依賴性。與統計學參數模型相比，基于分形幾何理論的表面分形模型具有自相似和尺度獨立的特性，克服了統計學模型尺度依賴性的缺陷，更能從本質上描述粗糙表面的特征[15-19]。軋制界面的三維分形表面采用修正的兩參數Weierstrass-Mandelbrot函數描述，其表達式為

(2)

式中，軋制界面粗糙形貌由尺度獨立的分形參數D和G控制。表面分形維數D，其物理意義是粗糙表面所占據的空間程度大小，D值越大對應于越密集的表面形態(更光滑的表面形貌)；表面分形粗糙度G是高度尺度參數，G值越大對應越粗糙的表面形貌。采用式(2)生成的軋輥各向同性三維分形表面，如圖3所示。對磨削加工得到的軋輥表面，其表面粗糙度一般為0.2～1.6 μm。

基于式(2)的粗糙表面分形模型獲得的粗糙界面接觸力和變形之間的關系為[20]

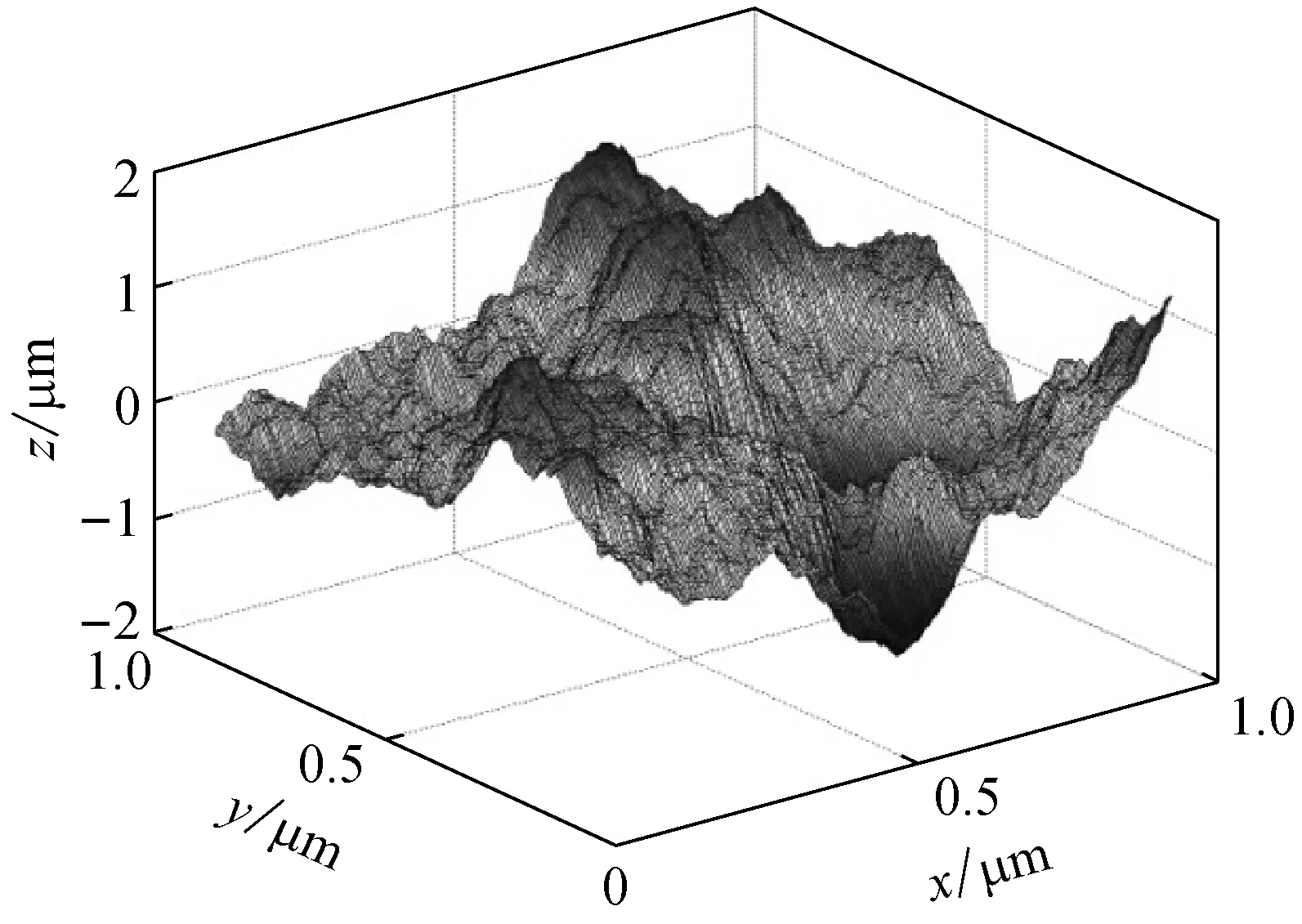
圖3 軋輥的三維分形粗糙表面示意圖

Fig.3 Three-dimensional Weierstrass-Mandelbrot fractal surfaces of roller

(3)

式中，δ表示變形量，系數k2和n取決于表面粗糙度和材料特性，剛度指數n的取值范圍一般為n=[1.0,2.7]。軋制界面粗糙形貌不同時，剛度指數n不同且n值隨軋制界面粗糙程度的增大而增大。當n=1.0時，式(3)的彈性回復力為線性，對應的動力系統為線性系統；當n=1.5時，式(3)對應于Hertz彈性接觸的回復力關系[21]。

1.3 軋機輥系非線性振動動力學方程

將獲得的粗糙軋制界面彈性回復力表達式(3)代入軋機系統垂直振動動力學方程式(1)，可得

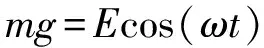
(4)

由于式(4)的非線性彈性回復力含有任意指數n，難以獲得其精確的解析解，而對軋制界面的垂直振動而言，通常情況是軋輥在靜平衡位置附近振動，為了獲得其振動響應的解析表達式，將軋制界面的彈性回復力fn(z,zs)在靜態平衡點z=0附近作三階泰勒展開，忽略高階項，獲得的近似非線性動力學方程可以表示為

(5)

并引入時間尺度τ=ωst，則式(5)對應的無量綱形式可表示為

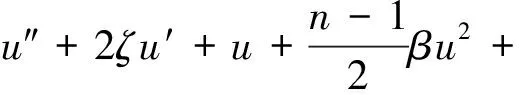
(6)

其中，β定義為非線性剛度率，其表達式為

(7)

式(7)顯示，非線性剛度率β反映了由軋制界面粗糙形貌引起的非線性剛度占系統總剛度的比例，0<β<1。在無接觸分離發生的初始位移范圍內，u≥-1。

2 考慮軋制界面粗糙形貌的軋機輥系固有頻率特性分析

軋機非線性振動系統的彈性回復力和無阻尼固有頻率特性隨軋制界面粗糙形貌的變化而變化。與式(6)對應的軋機輥系無阻尼自由振動方程為

(8)

其無量綱彈性回復力為

(9)

對式(8)所示的系統，采用多尺度方法(MMS)求解固有頻率。假設一個小參量ε，定義不同尺度的時間變量Tn=εnt，n=0,1,2,…，有

(10)

假設式(8)的解為

(11)

將式(10)和式(11)代入式(8)，并令ε，ε2和ε3項系數相等，可得

(12)

(13)

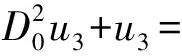
(14)

設式(12)的解為

(15)

將式(15)代入式(13)，可得

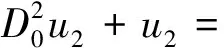
(16)

其中cc表示共軛，式(16)的解可以表示為

(17)

將式(15)和式(17)分別獲得的u1和u2代入式(14)，并消除久期項，得

(18)

假設

(19)

其中a和φ是關于T2的函數，將式(19)代入式(18)，并分離實部和虛部，可得

(20)

其中，φ0是常數。將式(15)，式(17)，式(19)和式(20)代入式(11)，得

(21)

其中

(22)

當無量綱初始條件為u(0)=U0，u′(0)=0時，φ0=0，得

(23)

將式(23)代入(22)，獲得的固有頻率表達式為

(24)

為了顯示軋制界面粗糙形貌對系統剛度和固有頻率的影響，選取不同的剛度指數，分別為n=nmin=1.0，n=1.5和n=nmax=2.7，計算軋機輥系系統彈性回復力和無阻尼固有頻率，并與Duffing振子描述的彈性回復力f(u)=u+1/3βu3和對應的系統固有頻率進行對比。無量綱彈性回復力-變形關系曲線，如圖4所示。圖4顯示，對于Duffing振子模型，當位移遞增時，系統剛度隨變形增大而增大，具有漸硬非線性，且彈性回復力-變形關系與軋制界面粗糙度無關；對于考慮界面粗糙形貌影響的軋機輥系系統，其無量綱彈性回復力-變形曲線的非線性度隨軋制界面粗糙度的增大而增大。圖4同時顯示，對于考慮軋制界面粗糙形貌的軋機輥系系統，由于其彈性回復力具有二次指數項，系統相對于靜平衡位置u=0具有非對稱特性：當位移向正方向遞增時，剛度隨變形增大而增大，系統為漸硬非線性；反之，當位移向負方向遞增時，剛度隨變形增大而減小，系統為漸軟非線性。而對Duffing振子描述的彈性回復力而言，系統相對于靜平衡位置u=0是對稱的：位移向正方向或負方向遞增時，系統剛度均增大，系統具有漸硬的非線性特性。

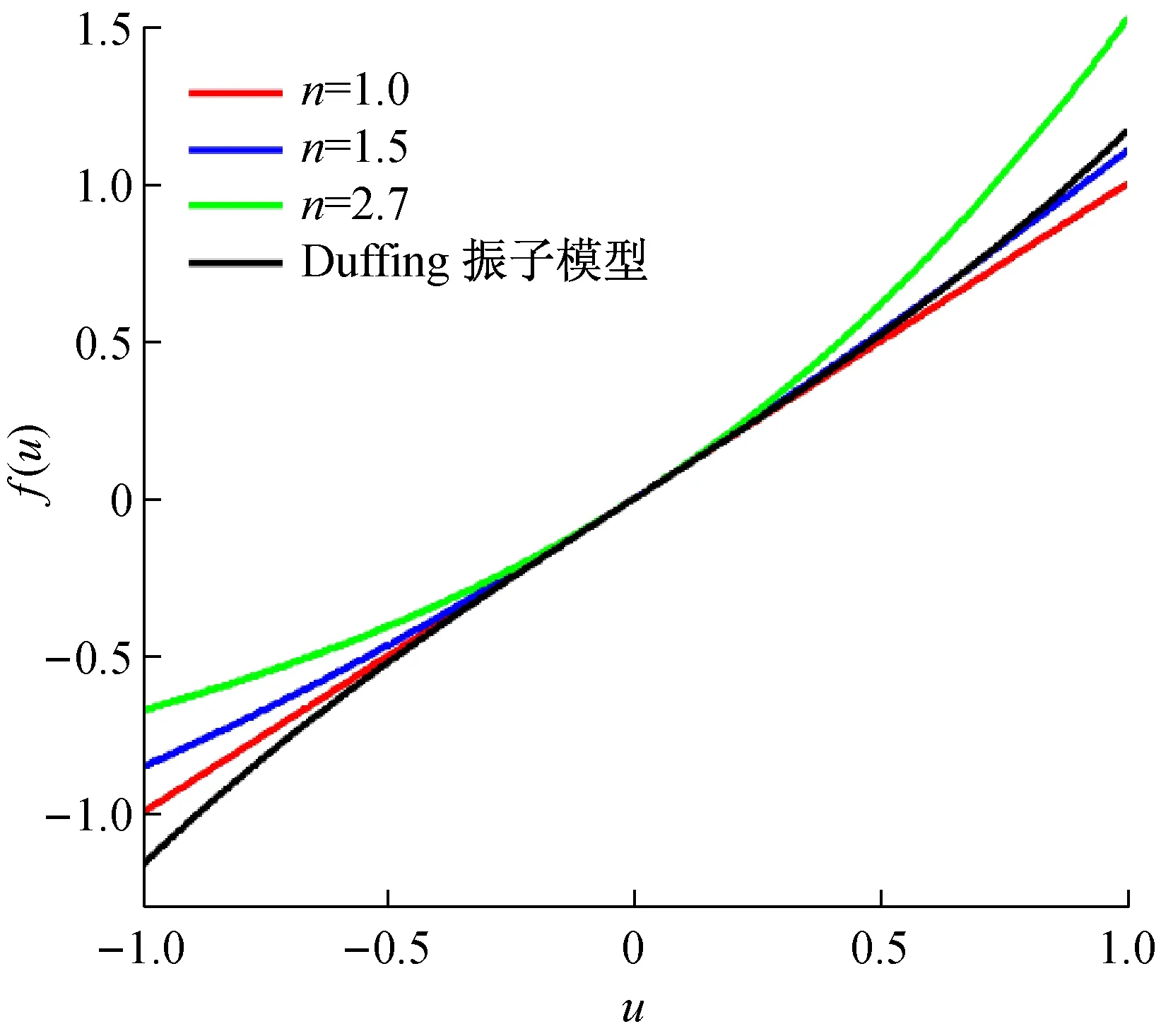
圖4 無量綱彈性回復力-變形關系曲線

對具有不同粗糙形貌軋制界面的軋機輥系系統，其固有頻率隨初始位移的變化關系曲線，如圖5所示。對于Duffing振子模型描述的軋機系統，最小固有頻率出現在靜平衡位置U0=0，由于系統剛度具有漸硬非線性特性，系統的固有頻率隨初始位移的增大而增大，即振動幅值越大，周期越短，且剛度指數n的變化對系統固有頻率特性無影響，Duffing振子模型描述的軋機系統的固有頻率與軋制界面粗糙形貌無關，因此用Duffing振子描述界面剛度的傳統軋機模型不能為生產實際提供準確的理論指導。對于考慮軋制界面粗糙形貌影響的軋機輥系系統，最大固有頻率出現在靜平衡位置U0=0，且固有頻率隨初始位移的增大而減小，即二次非線性和三次非線性項的疊加使系統非線性特性表現為漸軟非線性，振幅越大，周期越長。圖5同時顯示，對于n=1的線性系統，系統固有頻率為恒定值Ω0=1，與初始條件無關。當剛度指數n>1.0時，隨著初始位移向正方向或負方向偏離靜平衡位置，固有頻率均減小(Ω0<1)：對剛度指數n=1.5，固有頻率的最大減小量約為2%；對最大剛度指數n=nmax=2.7，固有頻率的最大減小量約為3%，因此固有頻率的變化量隨非線性剛度指數的增大而增大，表明固有頻率的變化量隨軋制界面粗糙程度的增大而增大。

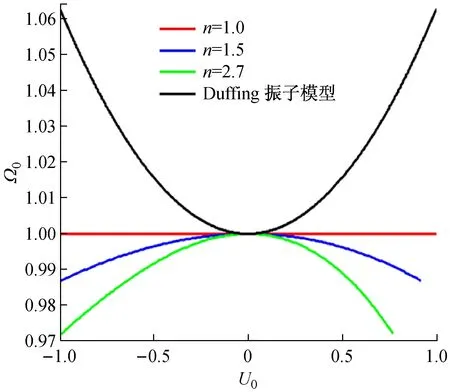
圖5 無阻尼自由振動系統固有頻率隨初始位移變化曲線

Fig.5 The normalized natural frequency as a function of the initial amplitude

3 軋機輥系非線性動力學響應特性分析

對于考慮軋制界面粗糙形貌影響的軋機輥系系統，其彈性回復力和固有頻率特性表明，系統具有漸軟非對稱的非線性特性。當軋機輥系系統受簡諧激勵作用時，采用多尺度法求解系統主共振的幅頻響應方程，假設式(6)所示系統的解為

(25)

軋機系統主共振時激勵頻率接近于系統固有頻率，令

(26)

將式(25)和式(26)代入式(6)，并令相應的ε0，ε1和ε2項系數相等，得

(27)

(28)

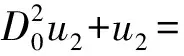
(29)

設式(27)的解為

(30)

將式(30)代入式(28)，可得

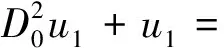
(31)

消除式(31)中的久期項，其解為

(32)

將式(30)和式(32)分別獲得的u0和u1代入式(29)，并消除久期項，得

(33)

令A=1/2U1exp(iφ)，代入式(33)，并分離實部和虛部， 得到系統主共振時響應幅值與激勵頻率之間的關系表達式為

(34)

由于系統具有非線性特性，因此外擾力頻率緩慢變化時系統存在振幅跳躍現象。為了保證式(34)的幅頻響應具有解，需滿足

(35)

當振幅U1到達峰值時式(35)等號成立，因此振幅向下跳躍點的幅值為

(36)

對應的向下跳躍頻率可以確定為

(37)

由于向上跳躍頻率Ωu與阻尼無關[22-23]，在式(34)中令ζ=0，可得

(38)

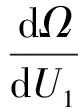
(39)

對應的向上跳躍頻率可以確定為

(40)

軋制界面的剛度指數分別為n=nmin=1.0，n=1.5和n=nmax=2.7時，系統主共振響應幅值U1與激勵頻率Ω之間的關系曲線，如圖6所示。其中，激勵幅值為F=0.01，阻尼比為ζ=0.005，非線性剛度率為β=0.5。圖6顯示，非線性剛度指數n增大，即軋制界面粗糙程度增大，幅頻響應曲線的非線性度增大，系統共振區域增大，該計算結果與通過實驗觀測獲得的帶鋼表面缺陷率隨軋制界面粗糙程度增大而增大的結論一致[24-25]。當剛度指數n=1.0時，系統為線性接觸振動系統，其幅頻響應曲線為單值曲線，曲線無彎曲，系統響應無突變。對剛度指數為n=1.5和n=nmax=2.7的非線性振動系統，由于系統具有漸軟非線性特性，其主共振幅頻響應曲線向左側彎曲，在同一激勵頻率下系統響應具有多值性，而多值解中的不穩定解(AC段、EG段)將會引起系統的響應幅值跳躍突變。當激勵頻率增大時，響應幅值突變跳躍到較大的值；當頻率減小時，響應幅值突變跳躍到較小的值。對剛度指數為n=2.7(n=1.5)的軋機非線性振動系統，當激勵頻率逐漸增加時，響應幅值從點A突變跳躍到點B(點E突變到點F)；當激勵頻率逐漸減小時，響應幅值從點C突變到點D(點G突變到點H)。

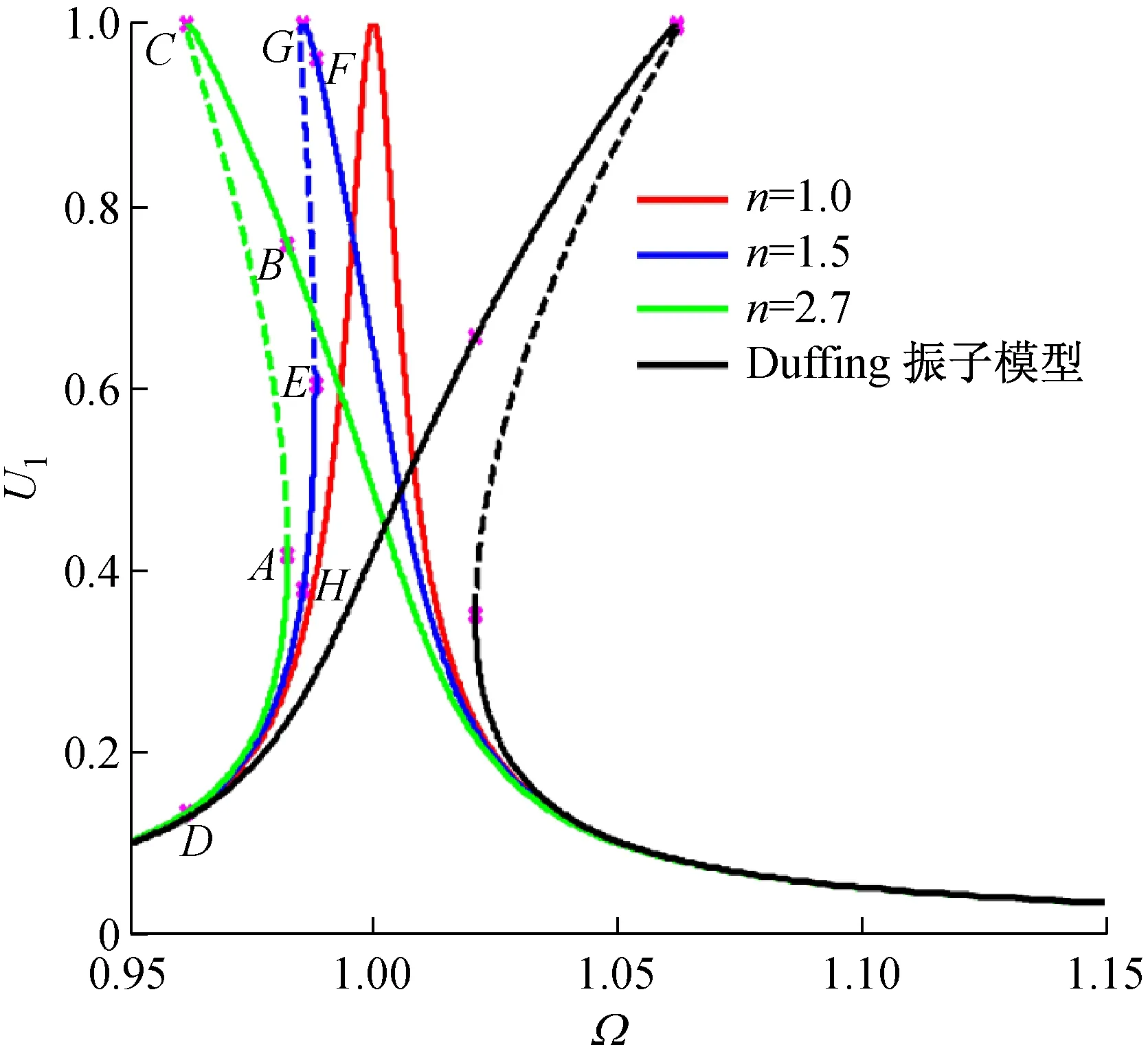
圖6 軋制界面粗糙形貌變化時主共振幅頻曲線

圖6同時顯示，幅頻響應曲線向左側彎曲的程度隨軋制界面非線性剛度指數n的增大而增大，振幅跳躍點對應頻率隨非線性剛度指數n的增大而減小，但振動幅值的峰值無變化。由于剛度指數n值隨軋制界面粗糙程度的增大而增大，因此軋制界面粗糙程度較大時，系統幅值跳躍頻率較小，達到穩定狀態時的振動幅值也較小。與考慮軋制界面粗糙形貌的軋機輥系系統相反，當軋制界面接觸剛度采用Duffing振子描述時，由于系統具有漸硬非線性，其幅頻曲線向右彎曲：當激勵頻率增大時，系統響應會出現向下跳躍的現象，振幅突變減小；當激勵頻率減小時，系統響應出現向上跳躍，振幅突變增大。

3.1 激勵載荷F對系統振動響應特性影響

式(34)所示的幅頻響應表達式顯示，系統的響應不僅與軋制界面粗糙形貌相關，而且與激勵載荷F、非線性剛度率β和阻尼比ζ相關。

對具有不同粗糙形貌軋制界面的軋機輥系系統，當激勵載荷F變化時，其主共振幅頻響應曲線，如圖7所示。其中，非線性剛度率為β=0.5，阻尼比為ζ=0.005。不同粗糙形貌的軋制界面對應的剛度指數為n=nmin=1.0，n=1.5和n=nmax=2.7，外部激勵載荷為F=0.01，F=0.02，F=0.03。圖7顯示，激勵載荷F的大小影響軋機系統的主共振激烈程度和非線性度：當F增大時，系統主共振的幅值增加，振幅跳躍幅值范圍增大，跳躍頻率減小，主共振區域增大，減小外擾力F可有效降低主共振的影響。圖7同時顯示，激勵載荷對系統響應的影響與軋制界面粗糙形貌有關，當剛度指數n=1.0時，系統始終表現線性特性，其幅頻響應曲線為單值曲線，曲線無彎曲，系統響應無突變；當界面粗糙度增大，即n>1.0時，系統幅頻響應曲線的非線性度增大，振幅跳躍頻率減小，主共振區域增大。

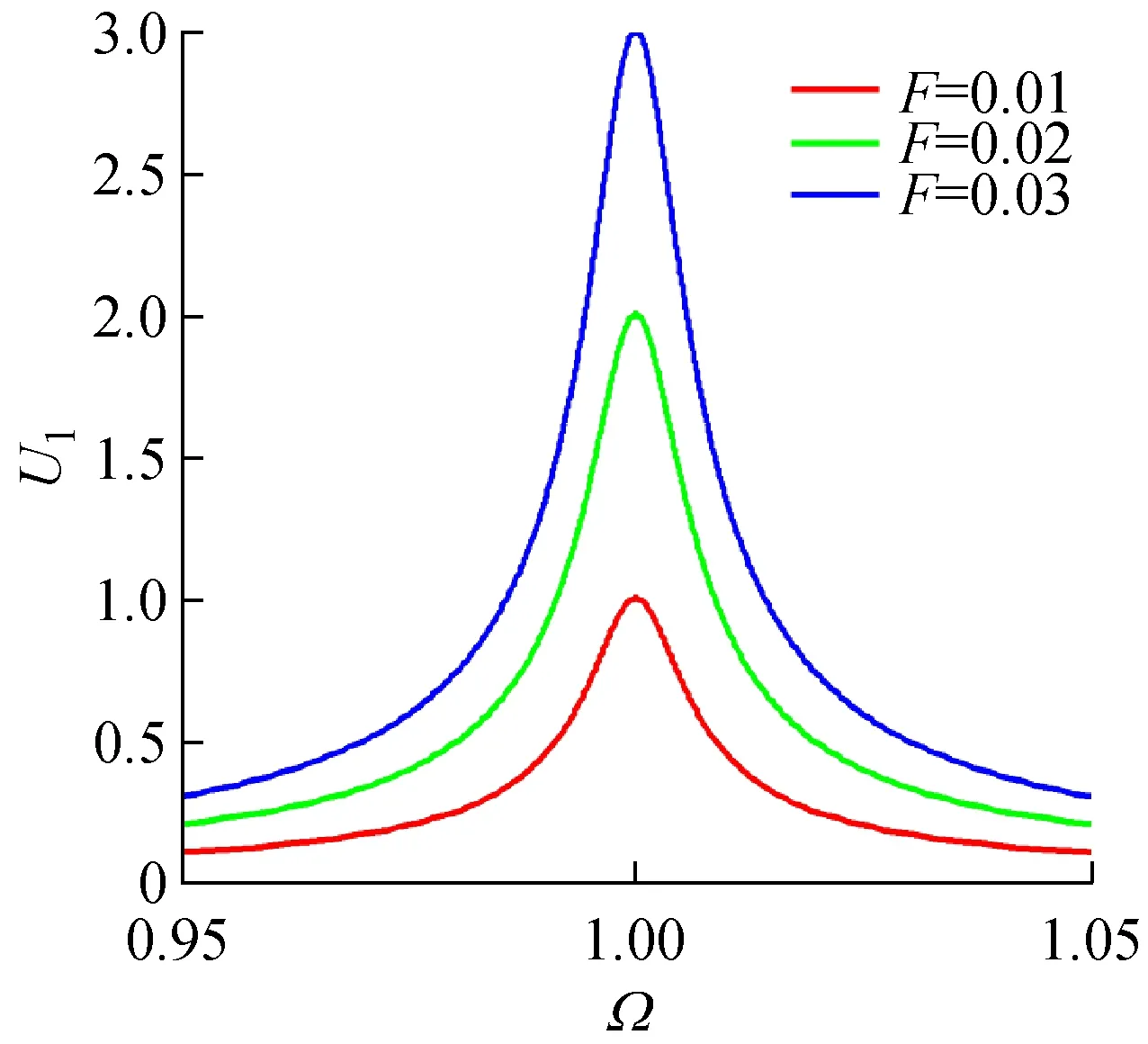
(a)n=1.0

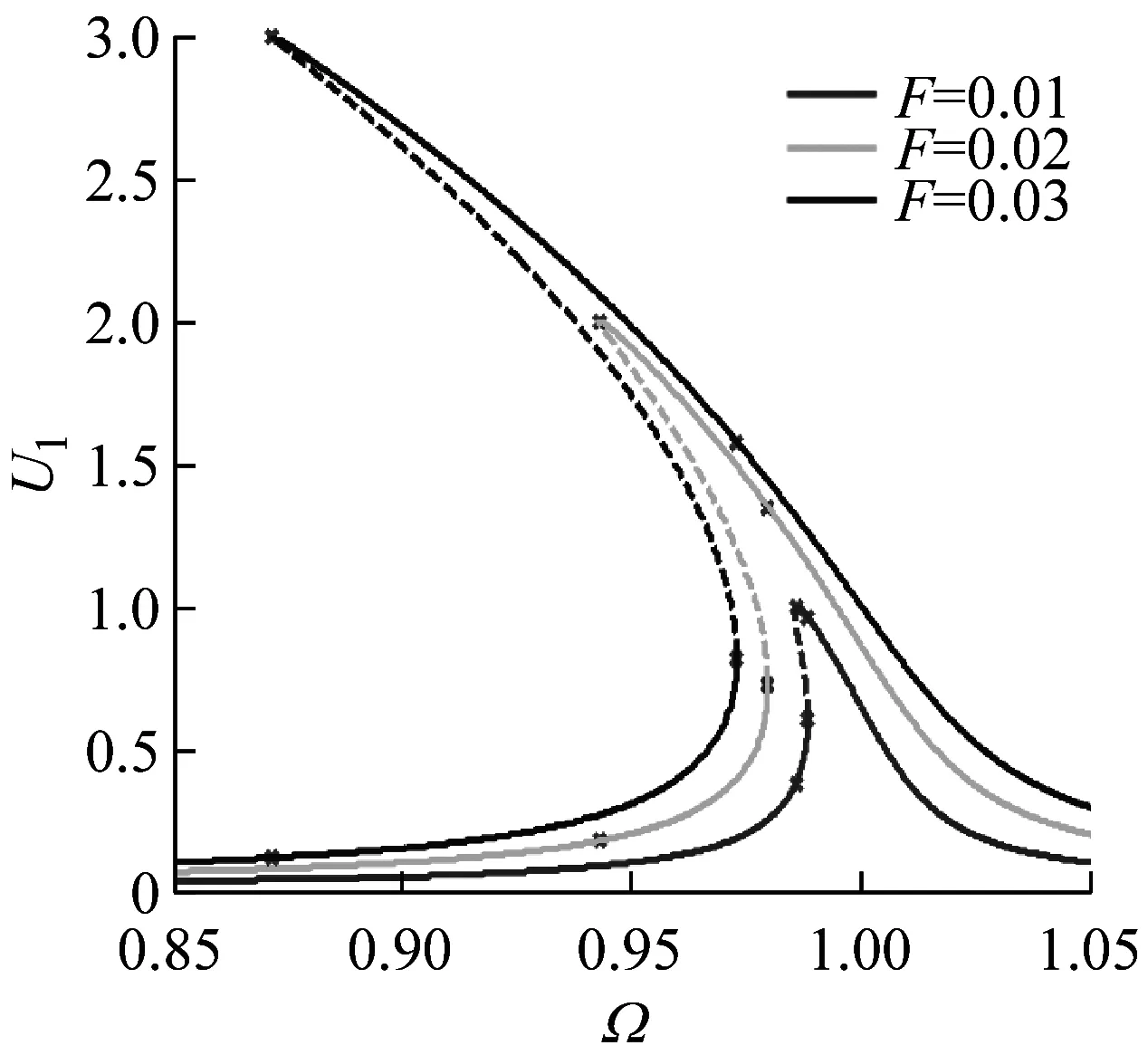
(b)n=1.5

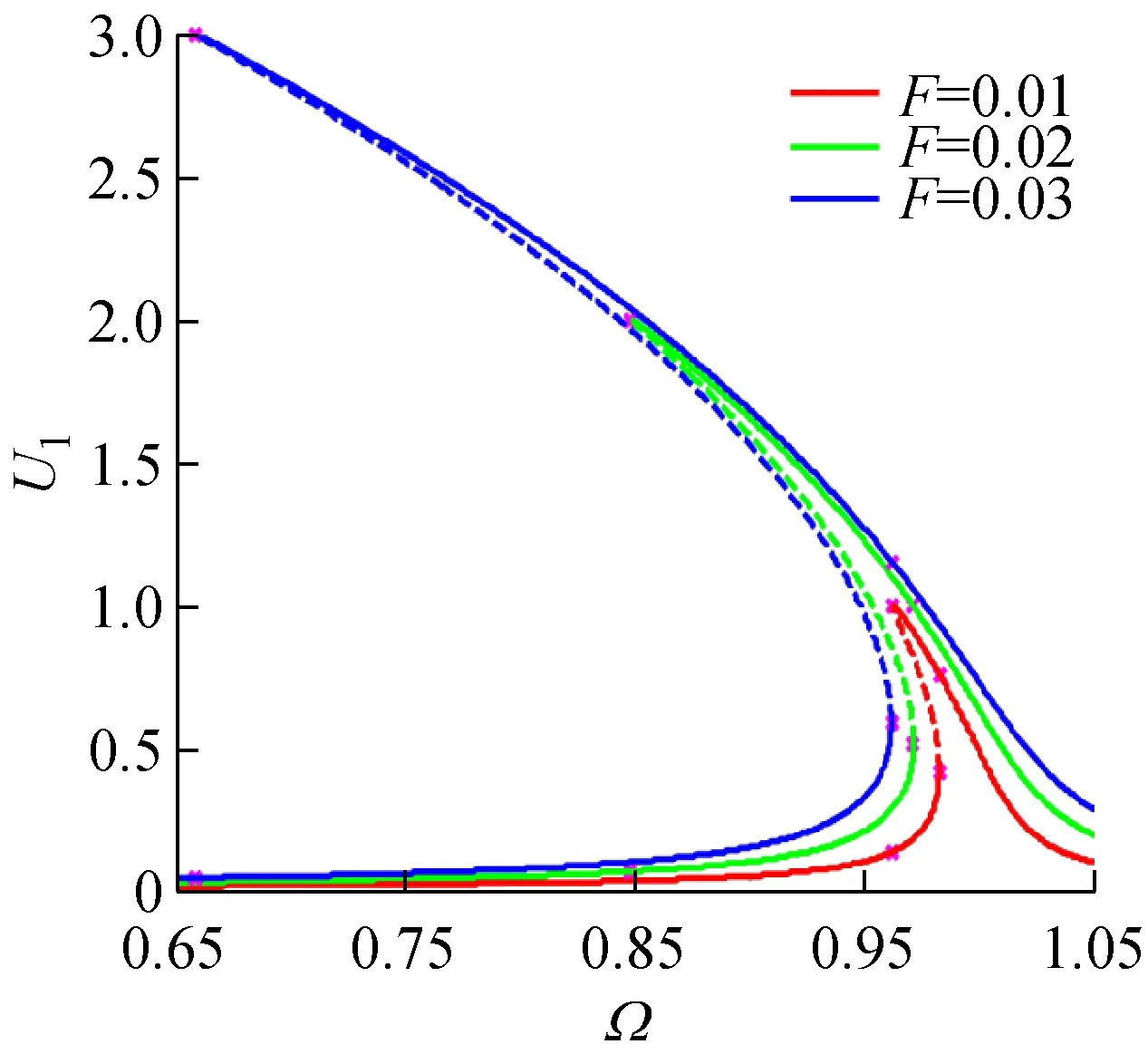
(c)n=2.7

3.2 非線性剛度率β對系統振動響應特性影響

對具有不同粗糙形貌軋制界面的軋機輥系系統，當非線性剛度率β變化時，其主共振幅頻響應曲線，如圖8所示。其中，激勵載荷幅值為F=0.01，系統線性阻尼比為ζ=0.005。圖8顯示，非線性剛度率β直接影響軋機輥系系統的非線性度:β=0時，軋機系統主共振無幅值跳躍，系統具有線性響應特性，隨著β的增大且n不為1時，共振曲線向左發生彎曲，系統幅頻響應曲線非線性度增大，振幅跳躍頻率減小，共振區域增大，但共振峰值始終不變。圖8同時顯示，系統非線性剛度率β對振動響應的影響與軋制界面粗糙程度有關，當剛度指數n=1.0時，系統始終表現線性特性；當界面粗糙度增大，即n>1.0時，主共振幅頻響應曲線的非線性度增大，系統振幅跳躍頻率減小，共振區域增大。

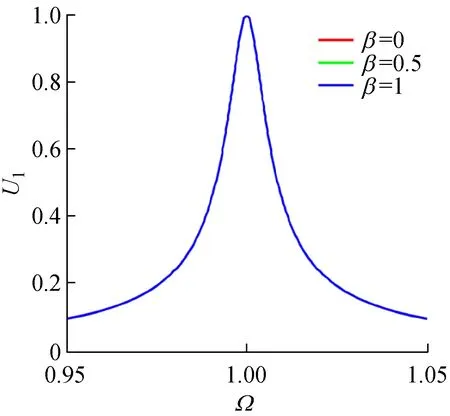
(a)n=1.0

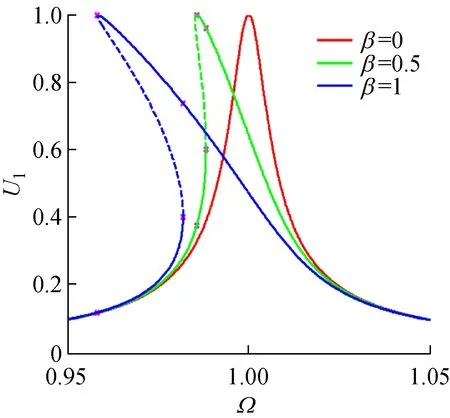
(b)n=1.5

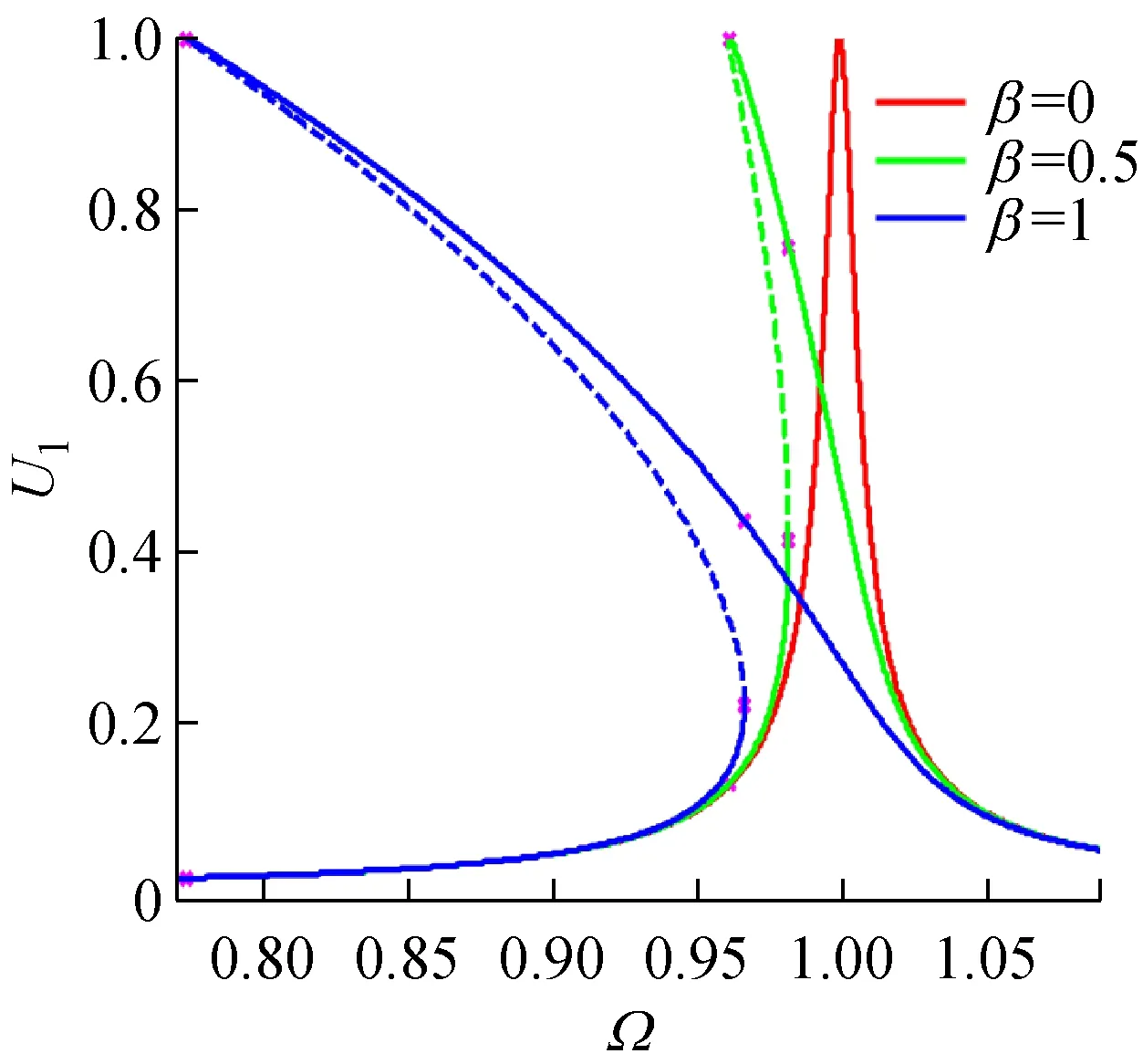
(c)n=2.7

3.3 阻尼比ζ對系統振動響應特性影響

對具有不同粗糙形貌軋制界面的軋機輥系系統，當系統線性阻尼變化時，其主共振的幅頻響應曲線，如圖9所示。其中，激勵載荷幅值為F=0.01，非線性剛度率為β=0.5。不同粗糙形貌軋制界面對應的剛度指數為n=nmin=1.0，n=1.5和n=nmax=2.7，系統阻尼比為ζ=0.003，ζ=0.004，ζ=0.005。圖9顯示，系統線性阻尼也影響軋機系統的主共振激烈程度和非線性度：當ζ增大時，系統主共振的振動峰值減小，振幅跳躍幅值范圍減小，幅頻響應曲線非線性度減小，主共振區域也減小，因此控制ζ的大小能有效地控制外擾對系統共振幅值的影響。圖9同時顯示，軋機輥系系統阻尼對振動響應的影響與軋制界面粗糙形貌有關：當剛度指數n=1.0時，系統始終表現線性特性；當軋制界面粗糙度增大，即n>1.0時，幅頻響應曲線的非線性度增大，跳躍頻率減小，主共振區域增大。

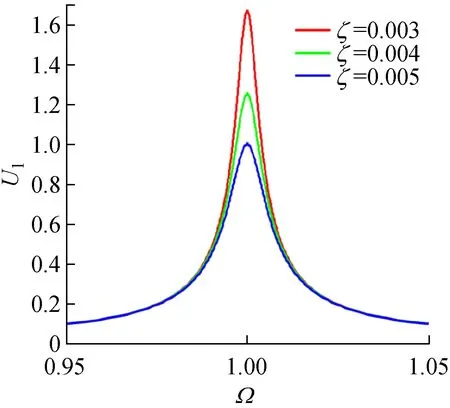
(a)n=1.0

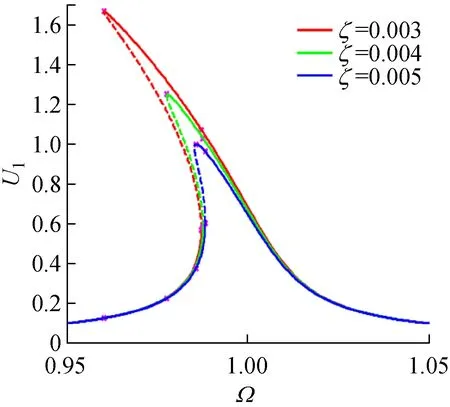
(b)n=1.5

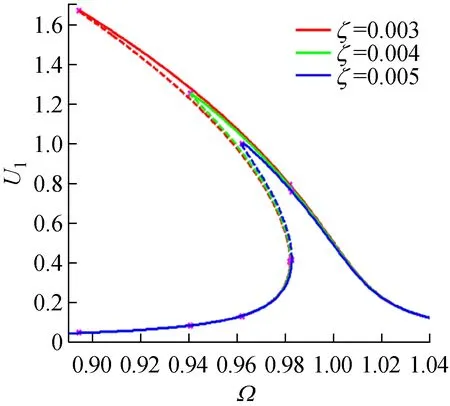
(c)n=2.7

4 結 論

本文通過建立考慮軋制界面粗糙形貌的軋機輥系系統非線性垂直振動模型，計算了具有不同粗糙形貌軋制界面的軋機輥系系統非線性剛度特性和固有頻率特性，并獲得了不同粗糙形貌軋制界面的軋機輥系系統跳躍頻率和幅值，分析了界面粗糙程度和系統主要參數對軋機輥系系統動力學響應特性的影響，結果顯示本文建立模型獲得的軋機輥系振動特性隨軋制界面粗糙形貌的變化規律符合實際生產情況。主要結論如下：

(1)對不同粗糙形貌的軋制界面，軋機輥系非線性振動系統的彈性回復力和無阻尼固有頻率特性隨軋制界面粗糙形貌的變化而變化，系統具有漸軟非線性特性。

(2)軋制界面粗糙形貌影響軋機系統主共振響應特性，激勵頻率增大時，振動響應幅值向上跳躍；當激勵頻率減小時，系統響應幅值向下跳躍。軋制界面粗糙程度較小的軋機輥系系統非線性度小，振幅跳躍頻率大，主共振區域小。

(3)軋制過程中激勵載荷波動較小、非線性剛度率較小、阻尼較大的軋機輥系系統，其主共振幅頻響應曲線非線性度小，振動幅值跳躍頻率大，主共振區域小。

[1] 鐘掘，唐華平. 高速軋機若干振動問題—復雜機電系統耦合動力學研究[J]. 振動、測試與診斷，2002, 22(1): l-8.

ZHONG Jue, TANG Huaping. High speed rolling mill vibration problems of complex mechanical and electrical system coupling dynamics[J]. Vibration, Measurement and Diagnosis, 2002, 22(1): l-8.

[2] YOUNES M A, SHAHTOUT M, DAMIR M N. A parameters design approach to improve product quality and equipment performance in hot rolling[J]. Journal of Materials Processing Technology, 2006, 171(1): 83-92．

[3] NIZIOL J, SWIATONIOWSKI A. Numerical analysis of the vertical vibration of rolling mill and their negative effect on the sheet quality[J]. Journal of Materials Processing Technology, 2005, 162(20): 546-550．

[4] YARITA I, FURUKAWA K, SEINO Y. An analysis of chattering in cold rolling of ultra thin gauge steel strip[J]. Transctions ISIJ, 1978, 19(1): 1-10.

[5] TAMIYA T, FURUI K, LIDA H. Analysis of chattering Phenomenon in cold Rolling[C]//Proceedings of the International Conference on Steel Rolling. Tokyo, 1980: 1191-1202.

[6] TLUSTY J, CHANDRA G, CRITCHLEY S, et al. Chatter in cold rolling[J]. CIRP Annals-Manufacturing Technology,1982,31(1):195-199.

[7] JOHNSON R E, QI Q. Chatter dynamics in sheet rolling[J]. International Journal of Mechanical Sciences,1994,36(7): 617-630.

[8] 楊旭，李江昀，童朝南. 冷軋機垂向輥系非線性振動建模與穩定性分析[J].振動、測試與診斷，2013,33(2):303-307.

YANG Xu, LI Jiangyun, TONG Chaonan. Modeling and stability analysis of nonlinear vibration of vertical roll system of cold rolling mill[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(2): 303-307.

[9] 陳勇輝，史鐵林，楊叔子. 四輥冷帶軋機非線性參激振動的研究[J]. 機械工程學報，2003,39(4):56-60.

CHEN Yonghui, SHI Tielin, YANG Shuzi. Study on parametrically excited nonlinear vibrations on 4-h cold rolling mills[J]. Chinese Journal of Mechanical Engineering,2003,39(4):56-60.

[10] TAMIYA T, FURUI K, LIDA H,et al. Analysis of chattering phenomenon in cold rolling[C]//International Conference on Steel Rolling, Vol. II, Science and Technology of Flat Rolled Products. Tokyo, 1980：1191-1202.

[11] SWIATONIOWSKI A, BAR A. Parametrical excitement vibration in tandem mills—Mathematical model and its analysis[J]. Journal of Materials Processing Technology, 2009, 134(2)：214-224.

[13] 侯東曉，劉彬，時培明，等. 分段非線性軋機輥系系統的分岔行為研究[J]. 振動與沖擊，2010，29(12)：132-135.

HOU Dongxiao，LIU Bin，SHI Peiming，et al. Bifurcation of piecewise nonlinear roll system of rolling mill[J].Journal of Vibration and Shock，2010，29(12)：132-135.

[14] 劉浩然，劉飛，侯東曉，等. 多非線性彈性約束下軋機輥系振動特性[J]. 機械工程學報，2012，48(9)：89-94.

LIU Haoran，LIU Fei，HOU Dongxiao，et al. Vibration characteristics of mill rolls under multi-segment nonlinear elastic constraints[J]. Journal of Mechanical Engineering，2012，48(9)：89-94.

[15] YAN W, KOMVOPOULOS K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics,1998,84(7):3617-3624.

[16] MAJUMDAR A, TIEN C L. Fractal characterization and simulation of rough surfaces[J]. Wear, 1990, 136(90): 313-327.

[17] BERRY M V, LEWIS Z V. On the Weierstrass-Mandelbrot fractal function[J]. Proceedings of the Royal Society A: Mathematical Physical & Engineering Sciences, 1980, 370(1743): 459-484.

[18] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces[J]. ASME Journal of Tribology, 1991, 113: 1-11.

[19] BLACKMORE D, ZHOU J G. Fractal analysis of height distributions of anisotropic rough surfaces[J]. Fractals, 1998, 6(1): 43-58.

[20] XIAO H F, SHAO Y M, BRENNAN M J. On the contact stiffness and nonlinear vibration of an elastic body with a rough surface in contact with a rigid flat surface[J]. European Journal of Mechanics A/Solids, 2015, 49:321-328.

[21] JOHNSON K L. Contact Mechanics[M]. Cambridge: Cambridge University Press, 1985.

[22] MALATKAR P, NAYFEH A H. Calculation of the jump frequencies in the response of sdof non-linear systems[J]. Journal of Sound and Vibration, 2002, 254(5): 1005-1011.

[23] BRENNAN M J, KOVACIC I, CARRELLA A,et al. On the jump-up and jump-down frequencies of the Duffing oscillator[J]. Journal of Sound and Vibration, 2008, 318(4/5): 1250-1261.

[24] 陳金山,李長生,曹勇.軋輥粗糙度對不銹鋼板帶表面和工藝參數的影響[J].機械工程學報, 2013, 49(4): 25-29.

CHEN Jinshan, LI Changsheng, CAO Yong. Effects of roll roughness on surface and process parameters for stainless-steel strip[J]. Chinese Journal of Mechanical Engineering, 2013,49(4):25-29.

[25] LENARD J G. The effect of roll roughness on the rolling parameters during cold rolling of an aluminium alloy[J].Journal of Materials Processing Technology, 2004,152(2)：144-153.

Nonlinear vibration characteristics of a rolling mill systemconsidering the roughness of rolling interface

SUN Yunyun, XIAO Huifang, XU Jinwu

(Collaborative Innovation Center of Steel Technology, Beijing University of Science and Technology, Beijing 100083, China)

The surface topography of the rolling interface can change the interface dynamics, and influences the dynamic response of a rolling mill system. Considering the roughness of the rolling interface, the nonlinear dynamic model of the rolling mill system was established. The nonlinear stiffness and natural frequency characteristics of the rolling system with different rough surface topography were calculated and compared with the traditional rolling mill model using Duffing oscillator to describe the interface stiffness. The main resonance amplitude-frequency characteristics of the rolling mill system were solved by using the method of multiple scales, and the expression of the jump frequency and the corresponding amplitude of the forced vibration response were derived. The influence of the rolling surface roughness, excitation load, nonlinear stiffness ratio and damping on the dynamic response characteristics of the rolling mill was analyzed. The results provide theoretical reference for suppressing rolling mill vibration.

rolling mill; vertical vibration; rough interface; nonlinear

國家自然科學基金青年基金項目(51304019);國家“十二五”科技支撐計劃項目(2015BAF30B01)

2015-12-21 修改稿收到日期：2016-03-24

孫韻韻 女，博士生，1993年6月生

肖會芳 女，博士，講師，1984年12月生

TH113

A

10.13465/j.cnki.jvs.2017.08.018