一類碰撞振動系統(tǒng)的激變和擬周期-擬周期陣發(fā)性
樂 源, 繆鵬程
(西南交通大學(xué) 力學(xué)與工程學(xué)院 應(yīng)用力學(xué)與結(jié)構(gòu)安全四川省重點(diǎn)實(shí)驗(yàn)室, 成都 610031)
一類碰撞振動系統(tǒng)的激變和擬周期-擬周期陣發(fā)性
樂 源, 繆鵬程
(西南交通大學(xué) 力學(xué)與工程學(xué)院 應(yīng)用力學(xué)與結(jié)構(gòu)安全四川省重點(diǎn)實(shí)驗(yàn)室, 成都 610031)
研究了一類三自由度碰撞振動系統(tǒng)的激變和陣發(fā)性。六維龐加萊(Poincaré)映射能夠表示成另外一個不對稱映射的二次迭代,這表明系統(tǒng)具有對稱性。該系統(tǒng)普遍存在發(fā)生Hopf分岔后得到的一對共軛擬周期運(yùn)動。根據(jù)動力系統(tǒng)的極限集理論,討論了極限集的對稱性,得到系統(tǒng)發(fā)生激變的條件,并引入一個距離函數(shù)判定對稱性恢復(fù)和激變臨界點(diǎn)。當(dāng)共軛混沌吸引子和不穩(wěn)定對稱不動點(diǎn)的最小距離等于0時,一對共軛混沌吸引子將會與不穩(wěn)定的對稱不動點(diǎn)在其吸引域邊界發(fā)生碰撞,從而導(dǎo)致激變。通過數(shù)值模擬,揭示了激變之后的一種新的陣發(fā)性動力學(xué)現(xiàn)象:擬周期-擬周期陣發(fā)性。其分岔機(jī)制是:兩個共軛擬周期吸引子→兩個共軛擬周期吸引子倍化→兩個共軛帶狀混沌吸引子→一個對稱混沌吸引子→一個對稱擬周期引子,通過對稱極限集理論來區(qū)分對稱吸引子和共軛吸引子,同時采用QR法計算Lyapunov指數(shù)并用來確定吸引子的類型。激變導(dǎo)致的擬周期-擬周期陣發(fā)性,對于多自由度碰撞振動系統(tǒng)的動力學(xué)研究及優(yōu)化設(shè)計具有重要意義。
碰撞振動系統(tǒng);擬周期運(yùn)動;激變;陣發(fā)性
具有對稱性的映射動力系統(tǒng)普遍存在對稱性恢復(fù)分岔,即:兩個或多個混沌吸引子融合并形成一個對稱混沌吸引子[1]。當(dāng)參數(shù)穿過激變臨界值時,兩個吸引子同時接觸吸引域的邊界。這意味著兩個吸引子與不穩(wěn)定鞍型軌道在吸引域邊界發(fā)生碰撞[2]。激變之后,系統(tǒng)的動力學(xué)行為展示出陣發(fā)性特征。激變誘發(fā)的陣發(fā)性這一概念用于描述動力系統(tǒng)在激變后出現(xiàn)的特殊動力學(xué)現(xiàn)象。文獻(xiàn)[3]的研究結(jié)果表明,所謂的對稱性破缺以及對稱性增長導(dǎo)致的吸引子的碰撞和爆發(fā),本質(zhì)都是共軛吸引子與對稱極限集之間發(fā)生碰撞的結(jié)果。然而,上述文獻(xiàn)關(guān)于激變之后誘發(fā)的陣發(fā)性動力學(xué)現(xiàn)象僅僅針對混沌-混沌陣發(fā)性,目前尚未見關(guān)于擬周期運(yùn)動的陣發(fā)性的研究和報道。通過研究一類具有對稱性的三自由度碰撞振動系統(tǒng)的激變和陣發(fā)性,首次揭示了激變之后的一種新的陣發(fā)性動力學(xué)現(xiàn)象:擬周期-擬周期陣發(fā)性。
碰撞振動現(xiàn)象廣泛存在于實(shí)際工程領(lǐng)域,例如齒輪的拍擊、引擎的錘擊、存在止擋沖撞的機(jī)械系統(tǒng)、船舶和浮體在波浪作用下的沖擊振動、機(jī)器人操作器與環(huán)境接觸和脫離引起的碰撞、航天器伸展系統(tǒng)由于關(guān)節(jié)間隙而發(fā)生沖擊等。由于存在碰撞,碰撞振動系統(tǒng)具有強(qiáng)非線性和非光滑性。研究碰撞振動系統(tǒng)的動力學(xué)行為對于機(jī)械系統(tǒng)的優(yōu)化設(shè)計和噪聲控制具有重要意義。非線性動力學(xué)的分岔和混沌的研究是近十幾年來非線性科學(xué)領(lǐng)域十分活躍的研究前沿[4-5]。隨著非線性動力系統(tǒng)理論、動態(tài)測試技術(shù)和計算機(jī)技術(shù)的迅速發(fā)展,碰撞振動系統(tǒng)的研究進(jìn)入了全新的階段。HOLMES等[6-7]考慮單自由度碰撞振動系統(tǒng),研究了周期運(yùn)動的存在性和穩(wěn)定性、分岔和混沌行為。對于多自由度碰撞振動系統(tǒng),在分岔點(diǎn)處可能同時存在兩種類型的分岔,這就導(dǎo)致了余維二分岔。各種分岔之間相互作用,對碰撞振動系統(tǒng)的局部動力學(xué)具有重要的影響。文獻(xiàn)[8-11]采用中心流型—范式理論和數(shù)值模擬的方法研究了各種余維二分岔,包括Hopf-flip分岔、Hopf-Hopf分岔以及各種強(qiáng)共振情況下的Hopf分岔。ZHANG等[12]對振動篩系統(tǒng)的兩類余維三分岔進(jìn)行了研究。當(dāng)系統(tǒng)某一參數(shù)穿過某個臨界值時,碰撞振動系統(tǒng)的振子將會以零速度與剛性約束發(fā)生碰撞。這種現(xiàn)象在碰撞振動系統(tǒng)中被稱為“擦邊”。在擦切點(diǎn)處,系統(tǒng)的龐加萊映射是不連續(xù)的,并且會產(chǎn)生由這樣的非光滑因素誘發(fā)的一些非典型的分岔[13-14]。近年來其他關(guān)于碰撞振動系統(tǒng)力學(xué)的研究參見文獻(xiàn)[15-17]。然而目前還未見關(guān)于碰撞振動系統(tǒng)的對稱性恢復(fù)和激變的研究報道。
文獻(xiàn)[18-19]的研究結(jié)果表明,具有對稱性的碰撞振動系統(tǒng)普遍存在一對共軛吸引子,并引入一個虛擬的隱式映射來捕獲這對共軛吸引子。通過研究三自由度碰撞振動系統(tǒng)的激變和陣發(fā)性動力學(xué)現(xiàn)象,引入一個距離函數(shù)判定激變臨界點(diǎn)。當(dāng)共軛混沌吸引子和不穩(wěn)定對稱不動點(diǎn)的最小距離接近0時,一對共軛混沌吸引子將會與不穩(wěn)定對稱不動點(diǎn)在其吸引域邊界發(fā)生碰撞,從而導(dǎo)致對稱性恢復(fù)和激變。數(shù)值結(jié)果表明,當(dāng)控制參數(shù)在一定區(qū)間變化時,共軛擬周期運(yùn)動將會恢復(fù)對稱性,并出現(xiàn)激變誘發(fā)的陣發(fā)性動力學(xué)現(xiàn)象。通過對稱極限集的概念來區(qū)分對稱吸引子和共軛吸引子,同時采用QR法計算Lyapunov指數(shù)并用來確定吸引子的類型。
1 力學(xué)模型,對稱性和Lyapunov指數(shù)
圖1表示一類軸向振動系統(tǒng)的力學(xué)模型。該系統(tǒng)有三個質(zhì)量塊M1,M2,M3,其中M2上在M3兩邊分別有一個剛性約束,因此是具有雙側(cè)剛性約束的三自由度碰撞振動系統(tǒng)。M2通過剛度為K2的線性彈簧與阻尼為C2的線性阻尼器與剛性平面相連。M1通過剛度為K1的線性彈簧,阻尼為C1的線性阻尼器與M2相連。M3通過剛度為K3的線性彈簧,阻尼為C3的線性阻尼與M2相連。質(zhì)量塊Mi(i=1,2,3)上作用振幅為Pi的簡諧激勵力。當(dāng)激勵力振幅很小時,系統(tǒng)做強(qiáng)迫振動,是一個線性系統(tǒng)。當(dāng)激勵力振幅增加到一定值時,M3會依次與M2上的兩個剛性約束發(fā)生碰撞,系統(tǒng)變成強(qiáng)非線性系統(tǒng)。碰撞以一個恢復(fù)系數(shù)R來描述。假設(shè)碰撞的時間很短,與激勵力的周期相比可以忽略不計。假定C1,C2,C3為比例阻尼。
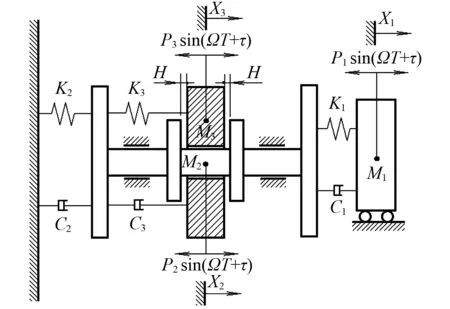
圖1 具有對稱剛性約束的三自由度碰撞振動系統(tǒng)Fig. 1 Three-degree-of-freedom vibro-impact system with symmetry
在任意兩次連續(xù)碰撞之間, 無量綱化的運(yùn)動微分方程為
(1)
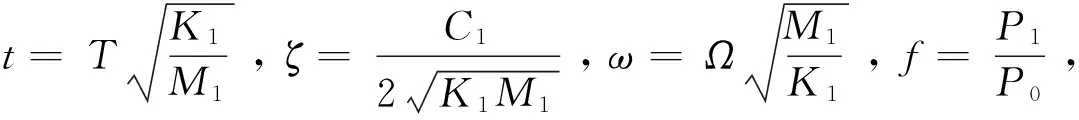
y2+=δ11y2-+δ12y3-,y3+=δ21y2-+δ22y3-
(2)

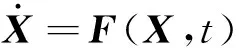
(3)
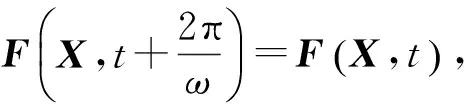
碰撞振動系統(tǒng)的相空間為
(4)
式中,S1為單位圓。把Poincaré截面選在與左邊剛性約束碰撞后的瞬時,即
(5)
定義變換
(6)
Poincaré映射P是由四個子映射組成的:①P1映射,質(zhì)量塊M3與左邊擋板碰撞后的瞬時運(yùn)動到到與右邊擋板碰撞前的瞬時所確定的映射;②P2映射,質(zhì)量塊M3與右邊擋板碰撞的過程;③P3映射,M3質(zhì)量塊與右邊擋板碰撞后的瞬時運(yùn)動到與左邊擋板碰撞前的瞬時所確定的映射;④P4映射,質(zhì)量塊M3與左邊擋板碰撞的過程。因此,Poincaré映射可以表示為
P=P4·P3·P2·P1
(7)
Poincaré映射的Jacobi矩陣為
DP=DP4(P3·P2·P1(X0))·DP3(P2·P1(X0))×
DP2(P1(X0))·DP1(X0)
(8)
令
Q=R-1Q1
(9)
式中,Q1為與左邊擋板碰撞后的瞬時運(yùn)動到與右邊擋板碰撞前的瞬時所確定的映射。則Poincaré映射可以寫為
P=Q2
(10)
式中,Poincaré映射P是映射Q的二次迭代。令TP(x*)=Dx*P為Poincaré映射在初始點(diǎn)x*處的Jacobi矩陣。則
(11)
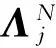
(12)
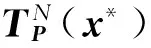
2 對稱不動點(diǎn)與對稱極限集
如果X*滿足P(X*)=X*,那么X*為Poincaré映射P的不動點(diǎn),對應(yīng)于系統(tǒng)的周期運(yùn)動。采用符號“(n,p)”來表示對稱碰撞系統(tǒng)的周期運(yùn)動。其中p為碰撞次數(shù),n為激勵力的周期數(shù)。因此,對稱周期(n,2)(n為奇數(shù))運(yùn)動表示n個激勵周期發(fā)生左右兩次對稱碰撞。對稱碰撞是指質(zhì)量塊M3與左右兩個擋板發(fā)生碰撞后,系統(tǒng)相應(yīng)的坐標(biāo)絕對值相等,方向相反。
定義1 (對稱不動點(diǎn))如果不動點(diǎn)X*滿足
X*=Q(X*)
(13)
則X*為Poincaré映射P的一個對稱(周期(n,2))不動點(diǎn),對應(yīng)于系統(tǒng)相應(yīng)的對稱周期(n,2)運(yùn)動。
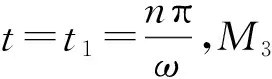
(14a)
(14b)
則存在對稱不動點(diǎn)。
定義2 (對稱極限集)如果X的ω極限集滿足
ωP(X)=ωP(Q(X))
(15)
則ωP(X)為對稱極限集。
引理1 如果ωP(X)是吸引子或者是周期解(不一定是吸引的),且滿足ωP(X)與ωP(Q(X))(即ωQ2k(X)與ωQ2k+1(X))的交集為非空,則ωP(X)是對稱ω極限集。
引理1表明,一對共軛吸引子ωQ2k(X)與ωQ2k+1(X)發(fā)生碰撞會產(chǎn)生一個單一的對稱吸引子。一對共軛吸引子互相碰撞意味著它們同時與不穩(wěn)定鞍形軌道(即不穩(wěn)定對稱不動點(diǎn))在吸引域的邊界發(fā)生碰撞。激變導(dǎo)致的陣發(fā)性是指吸引子尺寸突然變大并互相融合后產(chǎn)生的一種特殊動力學(xué)行為。在激變臨界點(diǎn)處,兩個共軛吸引子同時接觸吸引域的邊界。
3 對稱不動點(diǎn)的解析解和對稱性激變
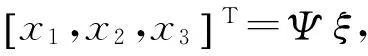
(16)
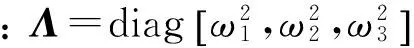
令φkj為矩陣Ψ中的元素,式(1)的解為
(17)
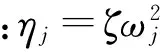
將式(17)代入式(14)得τ0,aj,bj的解為
(18a)
aj=Eajcosτ0+Fajsinτ0
(18b)
bj=Ibja1+Jbja2+Kbja3
(18c)
式中,Vc,Uc,Eaj,F(xiàn)aj,Ibj,Jbj,Kbj為系統(tǒng)參數(shù)確定的常數(shù)。將t=0和τ0,aj,bj代入式(17)得到對稱不動點(diǎn)的解X*=(x*1,y*1,x*2,y*2,x*3,y*3)。
這里不考慮Poincaré映射的擦邊分岔產(chǎn)生的奇異性。因此假定映射Q1,Q,P都是連續(xù)的和可逆的。相點(diǎn)X在P映射下的ω極限集為ωP(X),在Q映射下的ω極限集為ωQ(X)。極限集可以是吸引和排斥
的,定義吸引子為漸近穩(wěn)定的ω極限集。因?yàn)閄和Q(X)是一對共軛的映射點(diǎn),由X和Q(X)產(chǎn)生的ω極限集即ωP(X)和ωQ(X)稱為一對共軛的ω極限集。
點(diǎn)X在映射Q下的軌道為:X,Q(X),Q2(X),Q3(X),Q2k(X),Q2k+1(X),…由于映射P是映射Q的二次迭代,則有
Q2k(X)=Pk(X)
(19)
Q2k+1(X)=Pk(Q(X))
(20)
即映射Q的偶數(shù)次迭代即為點(diǎn)X在映射P下的軌道;而映射Q的奇數(shù)次迭代即為點(diǎn)Q(X)在映射P下的軌道。因此式(20)和式(21)隱含了ωQ2k(X)=ωP(X)和ωQ2k+1(X)=ωP(Q(X)),則有
ωQ(X)=ωP(X)∪ωP(Q(X))
(21)
又因?yàn)?/p>
Q(Pk(X))=Q2k+1(X)=Pk(Q(X))
(22)
則
(23)
即
Q(ωP(X))=ωP(Q(X))
(24)
式(15)等價于ωQ2k(X)=ωQ2k+1(X)。也就是說,如果X的ω極限等于它的共軛極限集,那么ωP(X)是對稱極限集。根據(jù)式(21),如果P和Q有相同的極限集,即ωP(X)=ωQ(X),那么它就是一個對稱的ω極限集。此外根據(jù)式(24),如果ωP(X)通過Q映射到自身,即Q(ωP(X))=ωP(X),則它是對稱ω極限集。
此處Poincaré映射P本身不能表現(xiàn)出對稱性,但是由式(15)可知非對稱映射Q能夠得到一對共存的共軛ω極限集,這表示碰撞振動系統(tǒng)具有對稱性。
為了找到發(fā)生激變的臨界點(diǎn),在兩個共軛吸引子與不穩(wěn)定對稱不動點(diǎn)X*(表示不穩(wěn)定對稱周期軌道)之間定義一個距離函數(shù)
(25)
式中:(x*1,y*1,x*2,y*2,x*3,y*3)為不穩(wěn)定對稱不動點(diǎn)的坐標(biāo);(x10,y10,x20,y20,x30,y30)為吸引子中點(diǎn)的坐標(biāo)。Dmin=0表示ωQ2k(X)與ωQ2k+1(Q(X))有非空交集,因此是激變的臨界點(diǎn)。
4 擬周期運(yùn)動的對稱性恢復(fù)和激變
4.1 擬周期吸引子的演變
考慮碰撞振動系統(tǒng)的系統(tǒng)參數(shù):n=1,ζ=0.008 6,R=0.85,h=0.06,um3=0.6,um2=2.8,um1=1,uk3=0.8,uk2=0.2,uk1=1,uf3=0.4,uf2= 0.5,uf1=1。取系統(tǒng)激勵力的頻率ω為控制參數(shù)。當(dāng)ω=3.05時,有兩個共軛擬周期吸引子,在相空間中表示兩個共軛的環(huán)面(見如圖2(a))。為了獲得一對共軛擬周期吸引子,需要給不穩(wěn)定對稱不動點(diǎn)X*(根據(jù)第3節(jié)計算)施加一個ΔX的擾動,并且通過映射Q對初始相點(diǎn)X=X*+ΔX進(jìn)行迭代。當(dāng)ω=3.05時,首先得到兩個不穩(wěn)定的共軛映射點(diǎn),然后分別在Poincaré截面上收斂到一對共軛的擬周期吸引子(在相空間中表示為一對共軛環(huán)面),見圖2(b)。當(dāng)控制參數(shù)增加到ω=2.985時,有一個單一的擬周期吸引子,見圖3。由于ωQ2k(X)=ωQ2k+1(X),所以圖3所示的擬周期吸引子是對稱的,映射點(diǎn)首先進(jìn)入對稱擬周期吸引子上部區(qū)域并停留一段時間,然后進(jìn)入下部區(qū)域并停留一段時間,如此循環(huán)。這種在對稱擬周期吸引子的兩部分無限交替的過程叫做激變誘導(dǎo)的擬周期運(yùn)動陣發(fā)性。這種擬周期運(yùn)動的陣發(fā)性現(xiàn)象只存在于多自由度對稱碰撞振動系統(tǒng)中,目前尚未見相關(guān)報道。圖2所示的一對共軛擬周期吸引子是如何演變成如圖3所示的單一的對稱擬周期吸引子的?這個問題的解答需要以吸引子的對稱性恢復(fù)分岔理論為基礎(chǔ)。
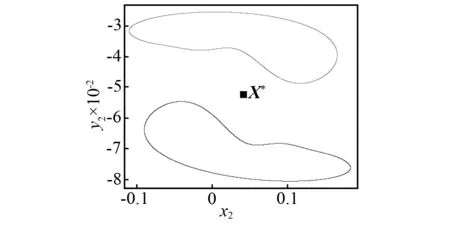
(a)一個不穩(wěn)定對稱不動點(diǎn)和一對共軛擬周期吸引子(迭代160 000次截取最后60 000個點(diǎn))
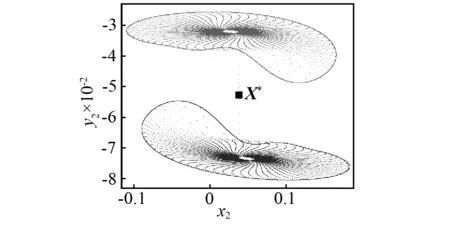
(b)從初始點(diǎn)X*+ΔX開始的整個收斂過程

圖3 一個對稱擬周期吸引子:ω=2.985(迭代160 000次截取最后60 000個點(diǎn))Fig.3 A symmetric quasi-periodic attractor:ω=2.985(plot the last 60 000 points after 160 000 iterations)
圖2所示的一對共軛吸引子有各自的吸引域,以通過不穩(wěn)定對稱不動點(diǎn)X*的吸引域邊界分開。
4.2 擬周期吸引子的激變和對稱性恢復(fù)分岔
當(dāng)ω增加到激變點(diǎn)ωc時,這對共軛吸引子就會擴(kuò)大和合并,最終產(chǎn)生一個單一的對稱吸引子。激變可以通過共軛吸引子與不穩(wěn)定對稱不動點(diǎn)的最小距離來檢測,這一距離函數(shù)由式(25)定義。當(dāng)ω=3.004 2時,由式(25)計算的距離D見圖4。結(jié)果表明當(dāng)參數(shù)ω=3.004 2時,最小距離為Dmin≈4×10-4,這一距離非常接近0。因此得出結(jié)論,在ω=3.004 2附近將發(fā)生激變。

圖4 擬周期吸引子與不穩(wěn)定對稱不動點(diǎn)之間的距離ω=3.004 2;Dmin≈4×10-4Fig.4 The distance between the quasi-periodic attractors and the unstable symmetric fixed point ω=3.004 2;Dmin≈4×10-4
當(dāng)控制參數(shù)ω減小時,Poincaré截面的投影相圖如圖5所示。當(dāng)ω=3.018時,首先發(fā)生環(huán)面倍化,產(chǎn)生一個如圖5(a)所示的2T環(huán)面。當(dāng)ω=3.016時,通過第二次環(huán)面倍化產(chǎn)生一個4T環(huán)面,如圖5(b)所示。當(dāng)ω=3.013時,將不會有環(huán)面倍化分岔,但是將會產(chǎn)生如圖5(c)所示的一對共軛的帶狀混沌吸引子。當(dāng)ω=3.01時,兩個共軛的帶狀混沌吸引子將會分別演化成一個帶狀混沌吸引子。如圖5(d)所示,看起來非常接近不穩(wěn)定不動點(diǎn)X*。當(dāng)ω=3.005時,共軛混沌吸引子將會大幅度擴(kuò)大并且會相互重疊,如圖5(e)所示。看起來它們已經(jīng)和不穩(wěn)定對稱不動點(diǎn)X*發(fā)生了碰撞。然而此時共軛吸引子與不穩(wěn)定對稱不動點(diǎn)的最小距離為Dmin≈8.5×10-3,這表明碰撞還沒有發(fā)生。在Poincaré截面的投影相圖上,這對共軛吸引子的重疊不能判斷它們之間的碰撞是否已經(jīng)發(fā)生,因?yàn)槿鐖D5所示的二維相圖僅僅是六維相空間的投影。當(dāng)ω=3.004 2時,類似的情況如圖5(f)所示。然而,在這種情況下,最小距離Dmin≈4×10-4(見圖4),這一距離非常接近0。當(dāng)ω=3.004 1時,兩個共軛的混沌吸引子已經(jīng)與不穩(wěn)定對稱不動點(diǎn)X*發(fā)生了碰撞,并且形成了一個單一的更大的混沌吸引子,如圖5(g)所示。這一結(jié)果再次證實(shí)了ωc=3.004 2是吸引子碰撞的臨界點(diǎn)。當(dāng)ω減小時,例如取ω=2.985,對稱混沌吸引子將會變成一個對稱擬周期吸引子,如圖5(h)所示。因此,擬周期運(yùn)動的對稱性恢復(fù)的路徑是:兩個共軛擬周期吸引子→兩個共軛擬周期吸引子倍化→兩個共軛帶狀混沌吸引子→一個對稱混沌吸引子→一個對稱擬周期吸引子。
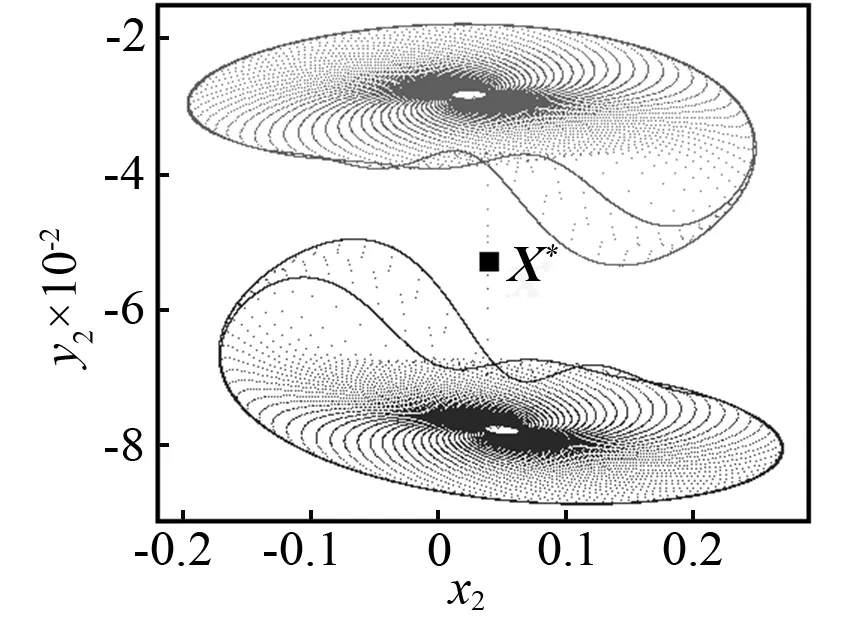
(a)ω=3.018
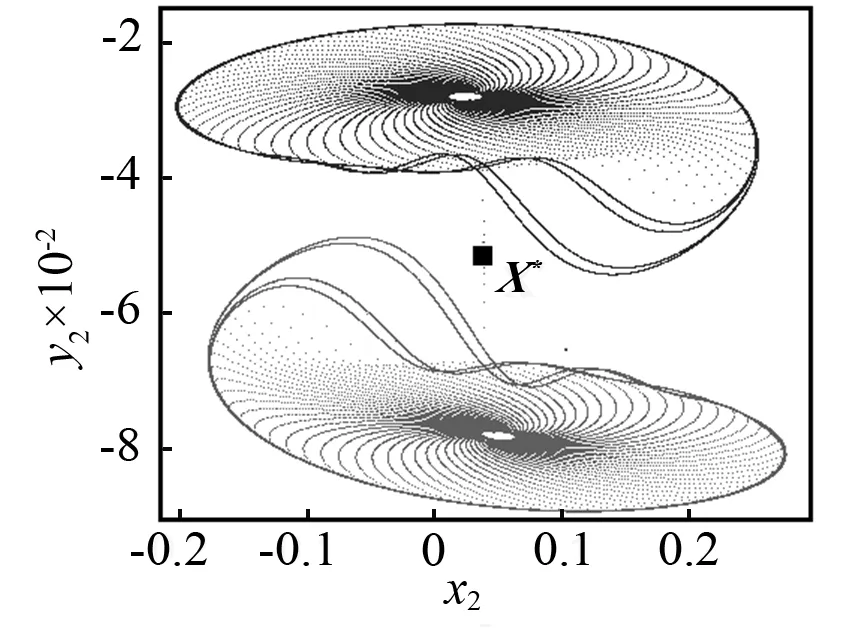
(b)ω=3.016
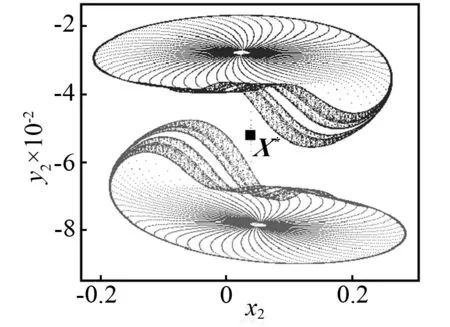
(c)ω=3.013
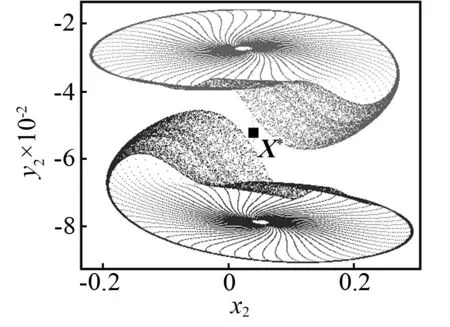
(d)ω=3.01
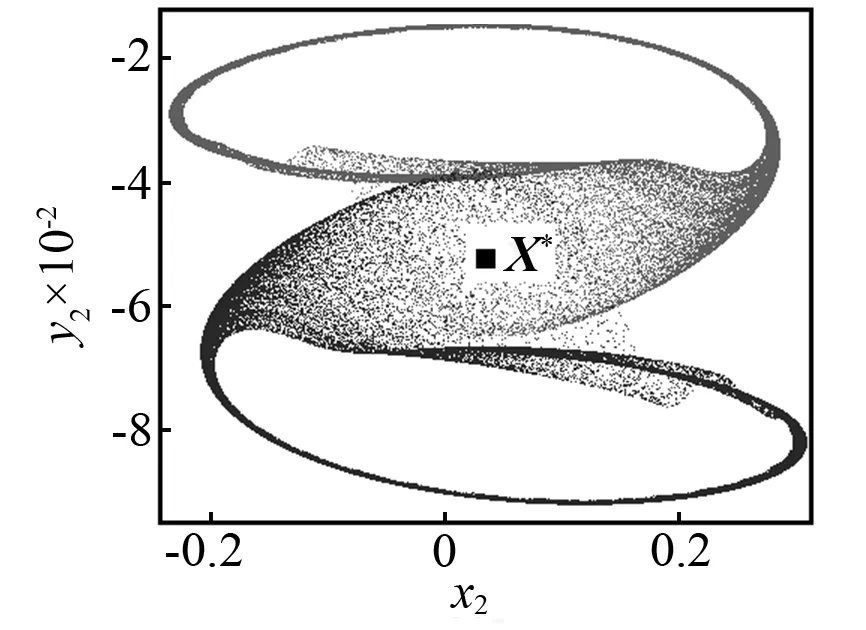
(e)ω=3.005
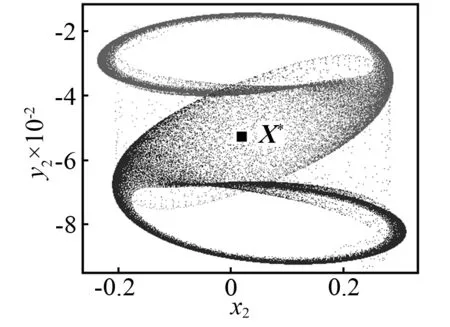
(f)ω=3.004 2
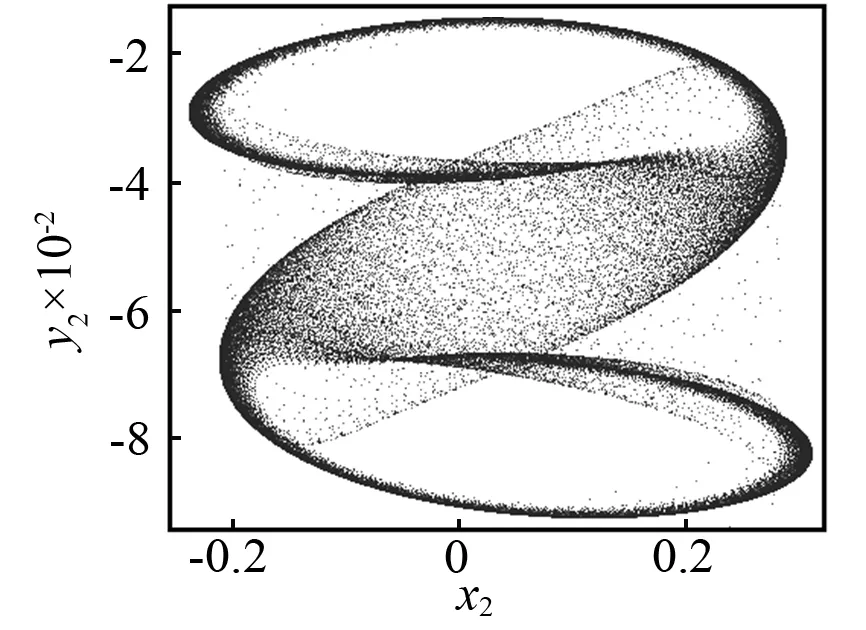
(g)ω=3.004 1
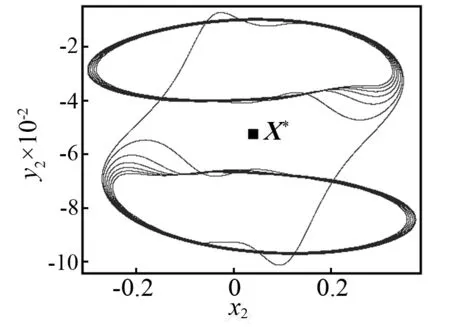
(h)ω=2.985
4.3 擬周期吸引子激變誘發(fā)的陣發(fā)性
由圖6可觀察到激變后誘發(fā)的陣發(fā)性。當(dāng)ω=3.004 1時,兩個共軛混沌吸引子同時與對稱不動點(diǎn)接觸,此時已經(jīng)發(fā)生激變,并導(dǎo)致混沌-混沌的陣發(fā)性,如圖6(a)所示。當(dāng)ω=2.985時,混沌-混沌陣發(fā)性轉(zhuǎn)變?yōu)閿M周期-擬周期陣發(fā)性,如圖6(b)所示。
以“2”節(jié)介紹的對稱極限集理論為基礎(chǔ),通過投影相圖可以區(qū)分對稱吸引子和共軛吸引子。很顯然,如圖5(a)~圖5(d)所示的兩個吸引子,因?yàn)棣豎2k(X)≠ωQ2k+1(X),所以這兩個吸引子是共軛的;因?yàn)棣豎2k(X)=ωQ2k+1(X),所以如圖圖5(f)和5(g)所示的兩個吸引子是對稱的。但是在Poincaré截面投影出現(xiàn)相互重疊的情況時,需要進(jìn)一步的判斷。例如,如圖5(e)和圖5(f)所示的吸引子,盡管兩個吸引子在某些區(qū)域內(nèi)重疊,但是它們并不是分布在整個區(qū)域,這就表示ωQ2k(X)≠ωQ2k+1(X),因此,吸引子在這兩種情況下是共軛的,但不是對稱的。
Lyapunov指數(shù)是一種判斷吸引子類型的有效工具,并采用第二節(jié)介紹的方法來計算。對于擬周期吸引子,至少有一個Lyapunov指數(shù)等于0。對于混沌吸引子,至少有一個Lyapunov指數(shù)大于0。可以通過如表1所示的Lyapunov指數(shù)來判斷吸引子的類型。結(jié)果表明,混沌吸引子產(chǎn)生于吸引子碰撞激變之后,且最大的Lyapunov指數(shù)總是大于0。

(a)ω=3.004 1
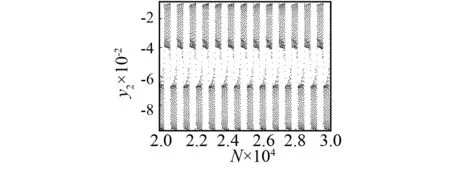
(b)ω=2.985

圖號λ1λ2λ3λ4λ5λ6吸引子的類型圖2(a)0.0000-0.0035-0.0487-0.0615-0.2307-0.4786擬周期圖5(c)0.00220.0000-0.0470-0.0636-0.2390-0.4756混沌圖5(e)0.00830.0000-0.0450-0.0666-0.2518-0.4671混沌圖5(g)0.00990.0000-0.0461-0.0655-0.2570-0.4653混沌圖3(a)0.0000-0.0013-0.0442-0.0442-0.2845-0.4255擬周期
5 結(jié) 論
對于對稱碰撞振動系統(tǒng),數(shù)值結(jié)果表明一對共軛擬周期運(yùn)動能夠轉(zhuǎn)變成單個對稱的擬周期運(yùn)動,并且在發(fā)生激變之后會出現(xiàn)擬周期運(yùn)動的陣發(fā)性現(xiàn)象。對稱性恢復(fù)和激變在這個轉(zhuǎn)換過程中具有關(guān)鍵作用。本文定義一個距離函數(shù)來確定激變臨界點(diǎn)。當(dāng)共軛吸引子與不穩(wěn)定對稱不動點(diǎn)在Poincaré截面上的最小距離為零時,一對共軛混沌吸引子將會同時與不穩(wěn)定不動點(diǎn)在吸引域邊界發(fā)生碰撞,這將會引起吸引子擴(kuò)大和合并。擬周期運(yùn)動的對稱性恢復(fù)機(jī)制是:兩個共軛擬周期吸引子→兩個共軛擬周期吸引子倍化 → 兩個共軛帶狀混沌吸引子 → 一個對稱混沌吸引子 → 一個對稱擬周期吸引子。
基于六維Poincaré映射能夠表示成另外一個非對稱映射的二次迭代,定義對稱極限集來區(qū)分對稱吸引子和共軛吸引子。QR法是一種連續(xù)正交化的手段,可以用于計算Lyapunov指數(shù),進(jìn)而判別吸引子的類型。
目前關(guān)于激變誘導(dǎo)的陣發(fā)性的研究,都集中在混沌-混沌陣發(fā)性,以及周期-周期陣發(fā)性[21-24]。本文揭示了碰撞振動系統(tǒng)中由于激變導(dǎo)致的擬周期-擬周期陣發(fā)性現(xiàn)象,這對于高維非線性動力系統(tǒng)吸引子的分岔研究以及碰撞振動系統(tǒng)的優(yōu)化設(shè)計,均具有一定的理論和實(shí)踐意義。
[ 1 ] CHOSSAT P, GOLUBITSKY M.Symmetry-increasing bifurcation of chaotic attractors[J]. Physica D Nonlinear Phenomena, 1988,32(3): 423-436.
[ 2 ] GREBOGI C, OTT E, YORKE J A.Chaotic attractors in crisis[J].Physical Review Letters, 1982,48(22): 1507-1510.
[ 3 ] BEN-TAL A. Symmetry restoration in a class of forced oscillators[J].Physica D Nonlinear Phenomena,2002,171(4):236-248.
[ 4 ] 王曉東, 陳予恕.一類電力系統(tǒng)的分岔和奇異性分析[J].振動與沖擊, 2014, 33(4): 1-6. WANG Xiaodong, CHEN Yushu. Bifurcation and singularity analysis for a class of power system[J]. Journal of Vibration and Shock, 2014, 33(4): 1-6.
[ 5 ] 于海,陳予恕,曹慶杰. 多自由度裂紋轉(zhuǎn)子系統(tǒng)非線性動力學(xué)特性分析[J].振動與沖擊, 2014, 33(7): 92-98. YU Hai, CHEN Yushu, CAO Qingjie. Bifurcation analysis for a nonlinear cracked multi-degree-of-freedom rotor system[J]. Journal of Vibration and Shock, 2014, 33(7): 92-98.
[ 6 ] HOLMES P J.The dynamics of repeated impacts with asinusoidally vibrating table[J].Journal of Sound and Vibration, 1982,84(2): 173-189.
[ 7 ] SHAW S W.Forced vibrations of a beam with one-sided amplitude constraint: theory and experiment[J].Journal of Sound and Vibration, 1985,99(2):199-212.
[ 8 ] LUO G W, XIE J H.Hopf bifurcation and chaos of a two-degree-of-freedom vibro-impact system in two strong resonance cases[J].International Journal of Non-Linear Mechanics,2002,37: 19-34.
[ 9 ] XIE J H, DING W C. Hopf-Hopf bifurcation and invariant torus of a vibro-impact system[J].International Journal of Non-Linear Mechanics,2005,40(4):531-543.
[10] DING W C, XIE J H.Dynamical analysis of a two-parameter family for a vibro-impact system in resonance cases[J].Journal of Sound and Vibration, 2005,287(1/2): 101-115.
[11] YUE Y, XIE J H.Neimark-sacker-pitchfork bifurcation of the symmetric period fixed point of the poincaré map in a three-degree-of-freedom vibro-impact system[J].International Journal of Nonlinear Mechanics,2013,48(2): 51-58.
[12] ZHANG Y X, KONG G Q, YIN J N. Two codimensin-3 bifurcations and non-typical routes to chaos of a shaker system[J]. Acta Physica Sinica,2008,57(10): 6182-6187.
[13] NORDMARK A B.Non-periodic motion caused by grazing incidence in an impact oscillator[J].Journal of Sound and Vibration,1991,145(2):279-297.
[14] MEHRAN K, ZAHAWI B, GIAOURIS D. Investigation of the near-grazing behavior in hard-impact oscillators using model-based TS fuzzy approach[J]. Nonlinear Dynamics, 2012, 69(3):1293-1309.
[15] 馮進(jìn)鈐, 徐偉. 碰撞振動系統(tǒng)中周期軌擦邊誘導(dǎo)的混沌激變[J]. 力學(xué)學(xué)報, 2013, 45:(1)30-36. FENG Jinqian, XU Wei. Grazing-induced chaostic crisis for periodic orbits in vibro-impact systems[J]. Chinese Journal of Theoretic and Applied Mechanics, 2013, 45(1): 30-36.
[16] GENDELMAN O V.Analytic treatment of a system with a vibro-impact nonlinear energy sink[J].Journal of Sound and Vibrations,2012, 331(21):4599-4608.
[17] 李飛, 丁旺才. 多約束碰撞振動系統(tǒng)的黏滯運(yùn)動分析[J]. 振動與沖擊, 2010, 29(5): 150-156.LI Fei, DING Wangcai.Analysis of the sticking motion in vibro-impact system with multiple constraints[J].Journal of Vibration and Shock, 2010, 29(5): 150-156.
[18] YUE Y, XIE J H, GAO X J.Capturing the symmetry of attractors and the transition to symmetric chaos in a vibro-impact system[J].International Journal of Bifurcation and Chaos,2012,22(5): 56-64.
[19] YUE Y, XIE J H, YUE Y.Lyapunov exponents and coexistense of attractors in vibro-impact systems with symmetric two-sided constraints[J].Physics Letters A, 2009, 373(23):2041-2046.
[20] ECKMANN J P, RUELLE D.Ergodic theory of chaos and strange attractors[J].Reviews of Modern Physics, 1985, 57(4):273-312.
[21] MANFFRA E F, CALDAS I L,VIANA R L, et al. Type-Ⅰintermittency and crisis-induced intermittency in a semiconductor laser under injection current modulation[J]. Nonlinear Dynamics, 2002,27(2):185-195.
[22] WERNER J P,STEMLER T, BENNER H. Crisis and stochastic resonance in Shinrili’scircuit[J]. Physica D Nonlinear Phenomena, 2008, 237(6):859-865.
[23] CHIAN A C L, REMPEL E L, ROGERS C. Complex economic dynamics: chaotic saddle, crisis and intermittency[J]. Chaos Solitons & Fractals, 2006, 29(5):1194-1218.
[24] TCHISTIAKOV V. Detecting symmetry breaking bifurcations in the system describing the dynamics of coupled arrays of josephson junctions[J].Physical D Nonlinear Phenomena, 1996, 91(1/2):67-85.
Crisis and quasiperiod-quasiperiod intermittency in a vibro-impact system
YUE Yuan, MIAO Pengcheng
(Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031,China)
Crisis and quasiperiod-quasiperiod intermittency in a 3-DOF vibro-impact system with symmetry were studied. The system’s 6-dimensional Poincaré map was expressed as the second iteration of another unsymmetric map, it implied that the system has a symmetry.Two conjugate quasi-periodic motions, coming from two conjugate periodic motions after Hopf bifurcation coexisted widely in such a dynamic system. According to the limit set theory of dynamic systems and the symmetry of the limit set, a distance function was introduced to detect the crisis of symmetry increasing. It was shown that when the minimum distance between a pair of conjugate chaotic attractors and an unstable symmetric fixed point is close to zero, a pair of conjugate chaotic attractors do not collide with the unstable symmetric fixed point on the attracting field boundary, to lead to a crisis. Numerical simulations revealed that a new intermittency behavior named the quasiperiod-quasiperiod intermittency occurs; the mechanism of symmetry restoring of quasi-periodic motion is two conjugate tori (quasi-periodic) → doubling of two conjugate tori → two conjugate band chaos attractors → a pair of symmetric chaos attractors → one symmetric torus (quasi-periodic); the symmetric limit set is introduced to distinguish symmetric attractors from conjugate ones; Lyapunov exponent spectrum computed with QR method is used to determine the type of attractors; the quasiperiod-quasiperiod intermittency is of importance for the optimization design of vibro-impact systems.
vibro-impact system; quasi-periodic motion; crisis; intermittency
國家自然科學(xué)基金資助(11672249;11272268;11172246)
2015-11-25 修改稿收到日期:2016-03-07
樂源 男,博士,教授,1974年2月生
O322
A
10.13465/j.cnki.jvs.2017.07.001

