非線性能量阱剛度優化計算與振動臺試驗

劉中坡， 呂西林， 王 棟， 烏建中

(1.同濟大學 機械與能源工程學院，上海 201804；2.同濟大學 土木工程防災國家重點實驗室,上海 200092)

非線性能量阱剛度優化計算與振動臺試驗

劉中坡1， 呂西林2， 王 棟2， 烏建中1

(1.同濟大學 機械與能源工程學院，上海 201804；2.同濟大學 土木工程防災國家重點實驗室,上海 200092)

介紹了一種通過幾何非線性產生非線性回復力的NES，并對它的寬頻控制特性進行了研究。通過解析方式求得1∶1共振下頻率與能量之間的關系并繪制頻率能量圖，頻率能量圖直觀的表達了當NES與線性振子連接到一起的時候，其相對于線性振子的振動頻率與系統中能量水平有著直接關系。在多自由度振動系統的模態空間中使用解析法將NES剛度與線性振子的能量、頻率與振型建立相關的表達式。由表達式得到振動系統在一定能量水平下，NES達到較優控制效果所需的非線性剛度。根據較優剛度計算方法，設計了NES振動控制試驗并進行振動臺試驗。為了試驗NES寬頻控制特性，振動臺臺面輸入采用了針對頻域測試的Chirp信號，試驗過程中通過改變NES的彈簧剛度與增加被控框架質量來改變框架動力學特性的方法以檢驗NES寬頻控制的效果。試驗結果表明NES有較好的寬頻控制效果，即使其剛度偏離優化值或被控對象動力學特性發生一定改變，NES依然能發揮較好的振動控制作用。

非線性能量阱；振動控制；振動臺試驗；非線性振動

振動控制裝置被廣泛用于航天、汽車、機械與建筑工程中，目前大多數振動控制裝置都是基于線性吸振器。隨著對非線性振動研究的深入，非線性吸振器由于其寬頻控制的特性引起了相關研究者們的廣泛關注。ROBERSON[1]最早提出了采用非線性振子作為吸振器進行振動控制,VAKAKIS等[2]將一個非線性振子與一個線性振子相連接,研究了系統在沖擊載荷下1∶1的共振響應，并提出非線性靶向能量傳遞現象，將該類剛度近似為立方剛度用于振動控制的非線性振子命名為“非線性能量阱”(Nonlinear Engergy Sink，NES)[3]。GOURDON等[4]通過數值方法驗證了該現象并指出NES優于傳統的線性調頻類吸振裝置。PANAGOPOULOS等[5]研究了具有多個自由度的線性振動系統與NES振子相連并發生1∶1共振時的共振頻率作用范圍的問題。GENDELMAN等[6]利用非線性分叉理論對NES的動力學特性進行分析，從而揭示了單自由度主振動系統連接NES后的各個分叉枝，為NES的減振機理研究提供了分析基礎；LEE等[7]采用經驗模態分解法對動力響應時程進行分解，繪制了頻率能量圖，這幾位研究者的成果為研究NES的振動控制提供了有效的工具。國內學者張也弛等[8-9]對引發最優靶向能量傳遞的條件與NES的參數優化做了研究，孔憲仁等[10]對兩自由度NES在簡諧荷載下的力學特性與振動控制效果使用數值方法進行了研究。陳勇等[11]使用數值仿真方法研究了NES在高聳結構振動控制中的應用。通過解析方式對試驗用框架在一定外界載荷作用下NES的剛度進行優化計算，求得較優的NES剛度后進行試驗驗證。在頻域中考查NES，并在較優與偏離優化值的剛度參數下獲得振動控制效果，通過改變試驗框架的質量來改變框架的動力學特性并考查NES的寬頻控制效果。

1 NES及其特性

1.1 NES結構與動力方程

NES由非線性回復力裝置、質量塊和阻尼器構成。利用線性彈簧，通過構造幾何非線性使其提供非線性的回復力(見圖1)。

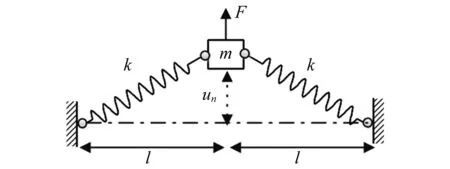
圖1 非線性振子實現方式Fig.1 Structure of nonlinear oscillator

質量塊m在平衡位置時由兩根剛度相同且等長的彈簧拉住，當彈簧受力沿中垂線移動到平衡位置，可以得到回復力與位移關系的表達式

(1)

式中：F為沿中垂線方向作用到質量塊的力；k為線性彈簧的剛度；un為質量塊相對絕對坐標系沿中線垂直方向的位移;l為彈簧被拉伸的長度。使用麥克勞林級數將式(1)展開得到式(2)

(2)

式中：l0為彈簧未受拉力下的原始長度，在質量塊m處于水平平衡位置，彈簧處于不受力的狀態時，l0=l；將l0=l代入式(2)得到質量塊m回復力近似表達式

(3)

式中：kn=k/l2；當質量塊位移un的絕對值在l長度40%以內時，式(3)的誤差在5%以內[12]。

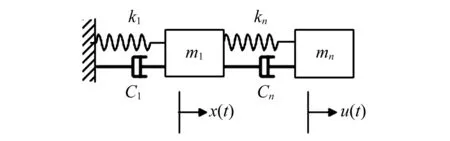
圖2 單自由度線性振子與NESFig.2 SDOF linear oscillator and NES

把NES與單自由度線性振子連接到一起，系統的動力學方程為

(4)

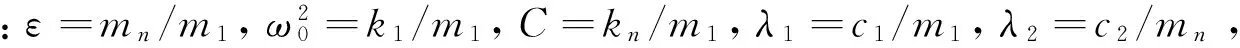
(5)

1.2NES連接到線性振動系統的動力學特性

NES在與線性系統連接到一起時，對線性系統的振動控制主要通過與線性振子發生內共振的方式實現的，內共振形式有：主共振、亞諧波共振和非線性拍振，這些共振形式并不是同時出現，而是隨系統能量水平的不同被激發，但其中起主要作用的是主共振。在目前的研究中大多數學者一般通過頻率能量圖描述NES的振動控制特性，本文對這種相對于以往非線性振動分析中常用的幅頻、相頻圖較新的工具使用解析的方法進行介紹，并使用頻率能量圖描述NES振動控制中起主要作用的1∶1主共振，由此來說明使用NES振動控制的時候，NES振動頻率與被控對象能量相關的聯系。這里的1∶1主共振指的是式(4)所定義的非線性微分方程在式(6)所定義的初始狀態下

x(-T/4)=u(-T/4)=0

(6)

式中，T為非線性微分方程式(4)周期解的周期值，滿足式(7)條件且半周期一致的周期解[13]。

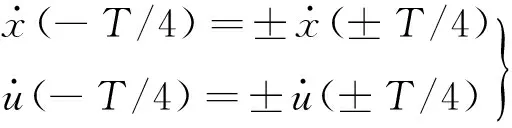
(7)

使用復化平均法來求解單自由度線性振子與NES連接到一起時候的1∶1共振[14]，定義復變量

(8)

由式(8)可以得到使用定義的復變量來表示的NES與線性振子的位移與加速度

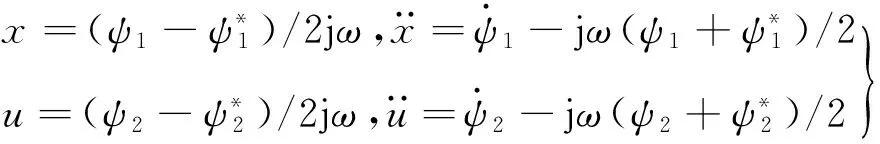
(9)

式(9)中*表示復變量的共軛關系，定義的復變量可以使用式(10)進行近似表達

ψ1(t)=φ1(t)ejωt,ψ2(t)=φ2(t)ejωt

(10)

將式(9)與式(10)代入式(5)可得到

(11)

根據復化平均法對式(11)消除快變頻率高于ω的項(e2jωt，e3jωt，…)，整理可得到

(12)

引入極坐標變換

φ1=Aejα,φ2=Bjβ

(13)

式中：A與B為實幅值；α與β為實相位。將式(13)代入式(12)之后，兩個方程的實部與虛部各自為0，得到4個方程。定義相位α=β與對時間t的微分為0，將4個方程整理得到方程組

(14)

整理式(14)中的第一個方程并積分可以得到

A2+εB2=N2

(15)

式中，N為積分常數，式(15)為保守系統中的全部動能。對式(14)方程組第二、第三個方程求解可以得到A、B的表達式，將其代入式(13)、式(10)與式(9)中的x與u的表達式，根據歐拉公式可以得到

(16)

根據式(16)可以得到保守系統的勢能與頻率之間的關系為

(17)

由式(17)得到的關系式，即可以在FEP(Frequency Energy Picture)中繪制S11±脊線的曲線。

1.3 頻率能量圖算例

考慮由式(4)定義并去掉阻尼項的一個保守系統的例子，令參數ε=0.05,C=1,ω∈[0.01～2]，并根據表達式(17)與式(16)在MATLAB中進行求解，由求解結果繪制NES的頻率與能量相關的曲線(見圖3)。

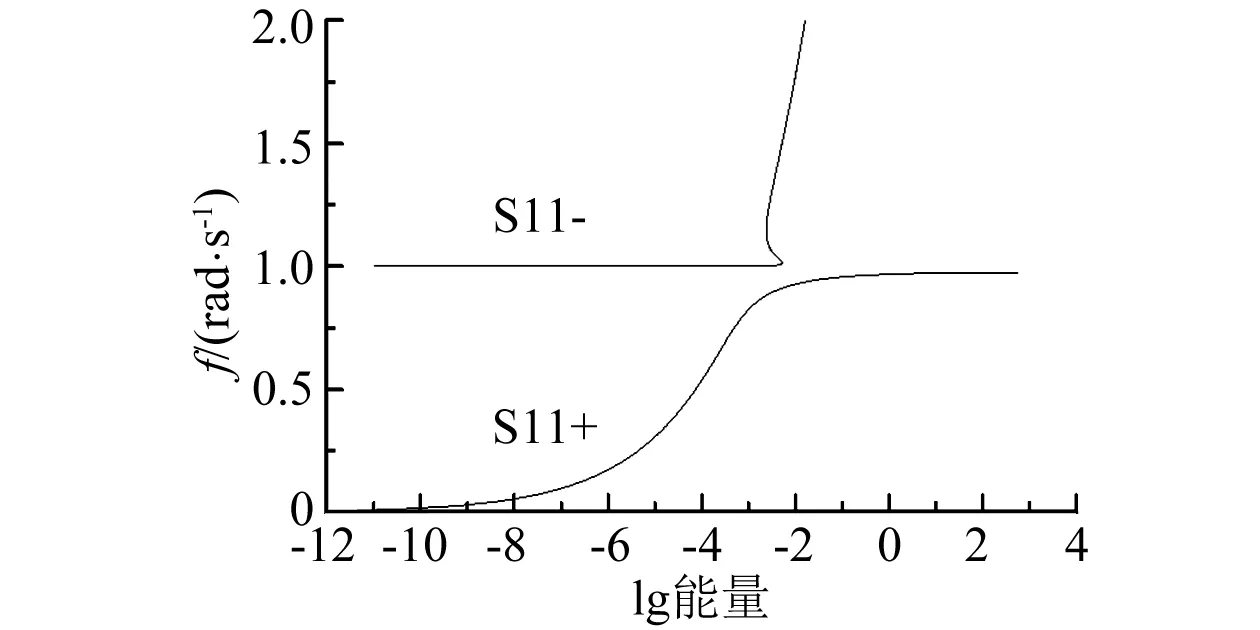
圖3 S11±脊線的頻率能量圖Fig.3 FEP of backbone branch S11±

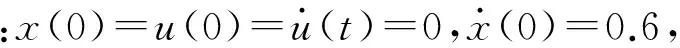
在時程數據中計算u-v，將得到的相對位移時程數據在MATLAB中進行小波變換，得到分解的各個振動頻率、頻率的幅值和時間序列，將這些數據通過時間序列與振動時程中系統總體的能量建立關系，得到圖5。圖5與中x軸為系統的動能與勢能之和，y軸為小波變換后分解得到的振動頻率，z軸為各個分解頻率能量。對照圖5可知，各個頻率的能量峰值對應系統能量的坐標值與S11+脊線所描述的關系基本一致，可以從圖5觀察出NES這種寬頻振動的特性。由此算例說明FEP，相對傳統的幅頻響應圖和相頻響應圖可以更為形象的描述非線性振動中頻率變化與系統能量變化的關系。且從圖5的分析結果，使用NES對被控目標特定頻率范圍的振動進行控制需要根據振動系統的能量水平來設計NES的參數。

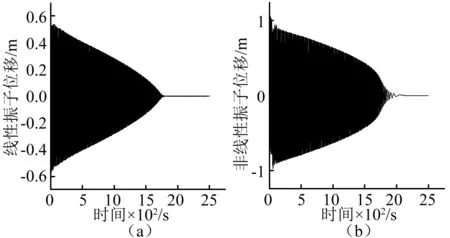
圖4 線性振子與NES的位移時程Fig.4 Displacement time history of linear oscillator and NES

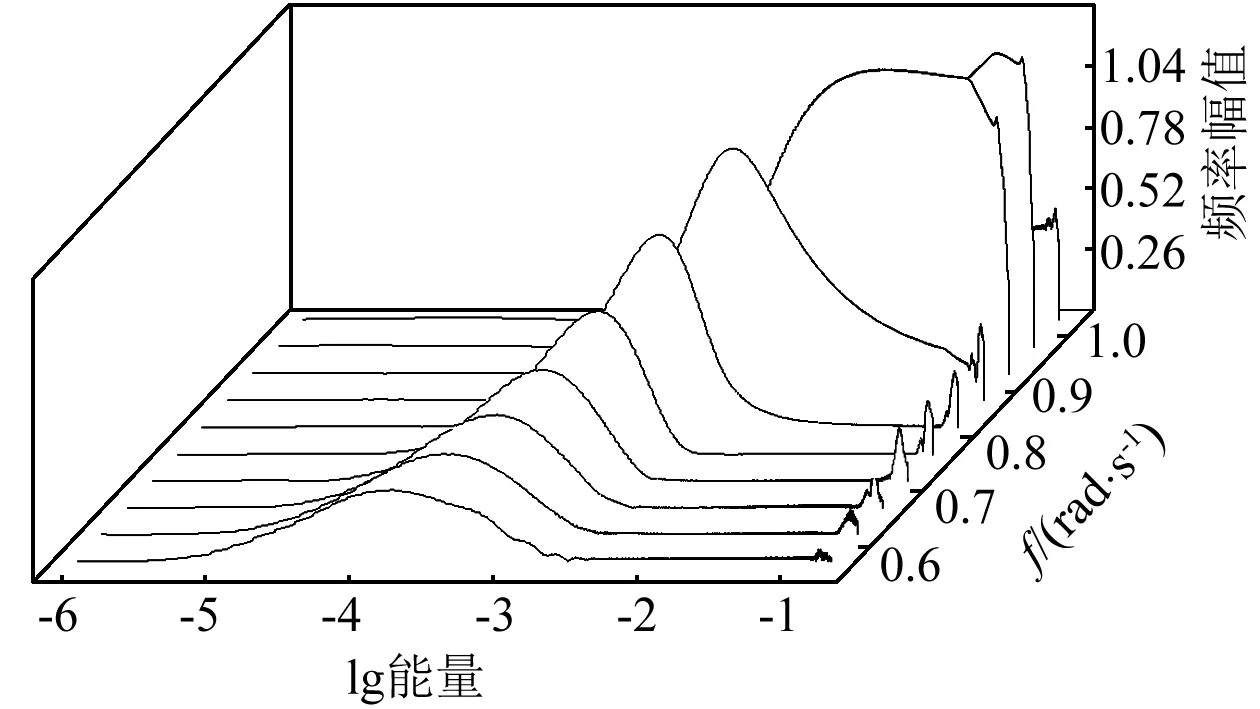
圖5 小波變換后各個頻率幅值與系統振動能量關系Fig.5 Variation of frequency amplitude with the variation of the system’s energy

2 NES剛度優化與仿真計算

2.1 NES剛度優化理論

從上述分析可以得出結論在使用NES進行振動控制時，需要針對線性振子的能量水平來設計NES的參數,不少文獻都涉及到NES參數優化的內容，在這里對NES的剛度優化推導過程做簡要介紹。為了優化單NES對多自由度線性振動系統的振動控制效果，需要建立起線性振子頻率、能量與NES剛度之間的聯系。除此之外，與其他被動振動控制裝置類似，為了獲得較好的振動控制效果，還需要結合被控系統的振型設計NES的安裝位置。

為了方便進行分析，將式(4)表達的動力學模型轉到集中質量多自由度振動系統的模態空間中。定義X=φq，φ為多自由度線性系統的模態振型矩陣，q為模態坐標向量。在本文中關注的是NES對試驗對象一階模態振動的控制，所以通過該式將方程轉換到一階模態空間之中， 如式(18)

(18)

式中：M*1,C*1,K*1分別為多自由度系統一階模態質量、阻尼與剛度；φn,1為歸一化之后一階模態振型在集中質量n處的值；q1為一階模態坐標；mn，u，kn和cn分別為NES的質量、位移、非線性剛度與阻尼。定義mn/M*1=ε，cn/M*1=ελn，kn/M*1=εΩω*40，C*1/M*1=ελ*和K*1/M*1=ω*0，代入式(18)中，并通過式(19)進行坐標變換

(19)

得到式(18)經過變換之后的近似表達式

(20)

使用式(8)與式(10)定義的復變量對s,vn進行替換，并使用式(21)定義的多尺度進行展開

(21)

展開之后消除久期項，并使用式(22)定義的極坐標變量替換復變量

(22)

得到方程

(23)

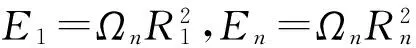
(24)

得到式(24)，通過該式將被控的線性振子能量水平與NES的參數：質量、剛度與阻尼聯系到一起，方便了對NES振動控制性能的研究。將式(24)的第二式兩側對En求偏導，得到E1和En的解析表達式

(25)

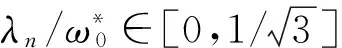
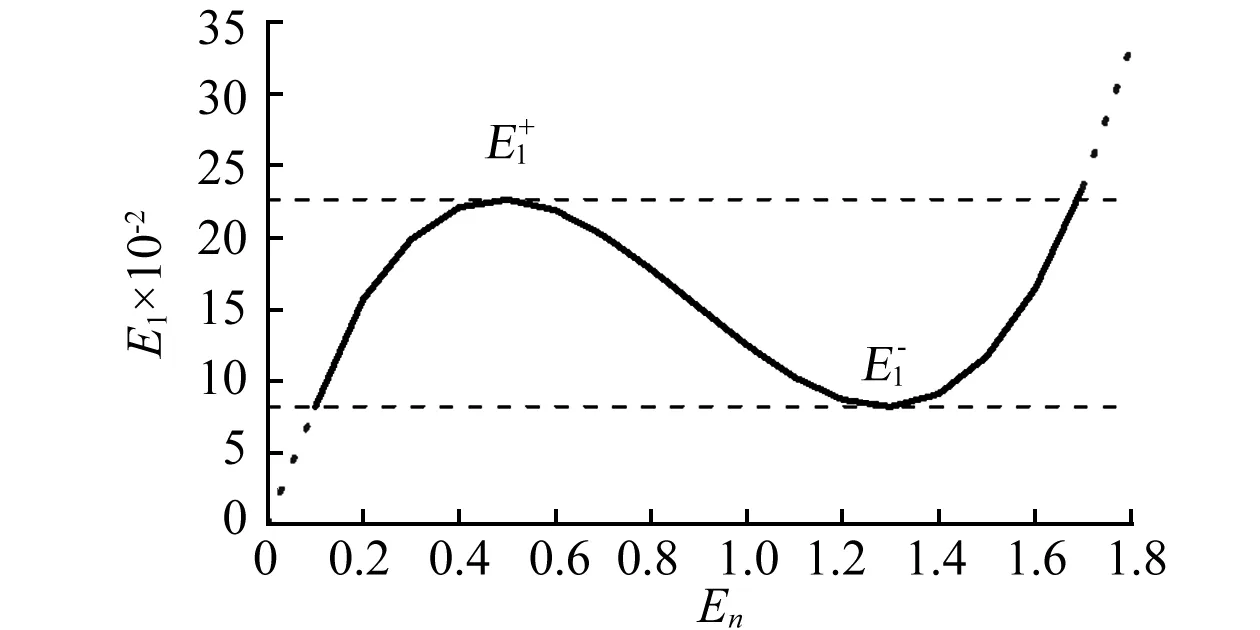
圖6 E1與En多重解關系Fig.6 Multiplicity solution between E1 and En

為了簡化極值點的表達式，定義以下變量

(26)

E1極值與對應En的值表達式為

(27)

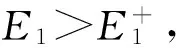
(28)

式(27)與式(28)建立關系，求得當滿足這個條件時的NES剛度表達式為

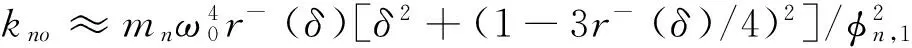
(29)

通過以上推導過程，得到了NES對一定能量水平的線性振子進行較優振動控制所需的剛度，為后面試驗設計提供了計算依據。

2.2 基于試驗對象的較優剛度參數仿真計算

由于在試驗過程中無法直接測得框架頂層的速度，而NES剛度優化計算又與線性振子的速度有關，所以采用數值仿真計算的方法來求得被控框架的速度。仿真計算的對象為試驗中使用的小型兩層框架，每層高度0.3 m、寬度0.25 m、質量4 kg，立柱為高0.6 m、寬0.15 m、厚1.2 mm的65Mn彈簧鋼板。試驗過程中使用振動測試系統中常用的Chirp信號對振動臺臺面進行基于位移的激勵，設定信號的幅值2 mm，頻率范圍為1～15 Hz。從振動臺控制系統中獲取到如圖7所示Chirp信號激勵下振動臺臺面實際的位移時程作為計算用的外部激勵，使用有限元軟件計算得到框架弱軸向的剛度陣和質量陣作為仿真計算用模型的參數，將這些數值帶入兩自由度線性振子動力學方程并在MATLAB中編寫方程積分計算的程序，計算程序中動力學微分方程的積分求解使用四階龍格-庫塔法?？蚣茉谙碌目湛蚣芩俣葧r程見圖8。

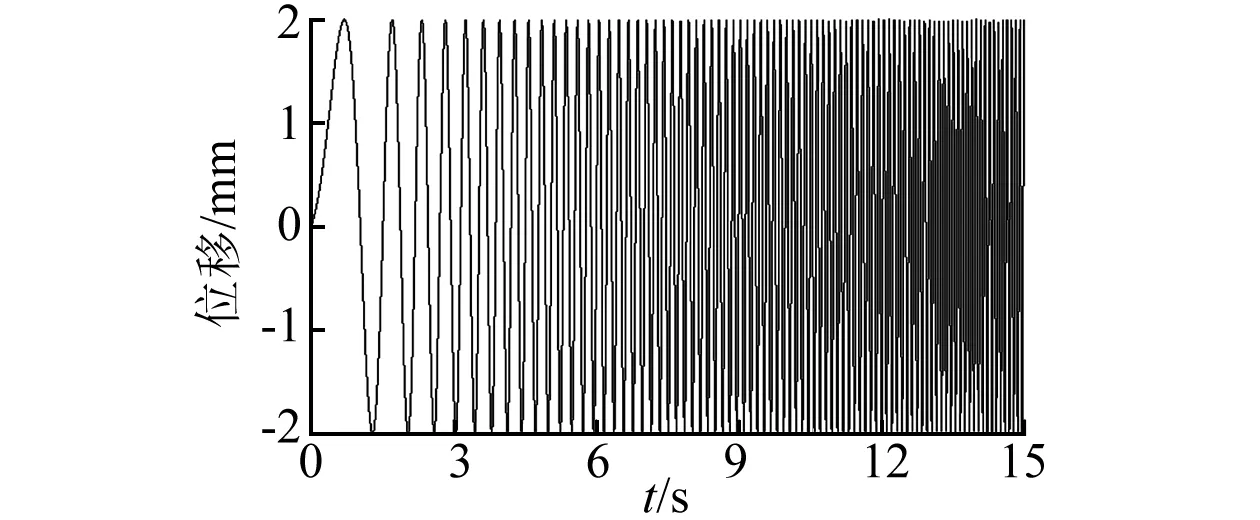
圖7 Chirp信號Fig.7 Chirp signal

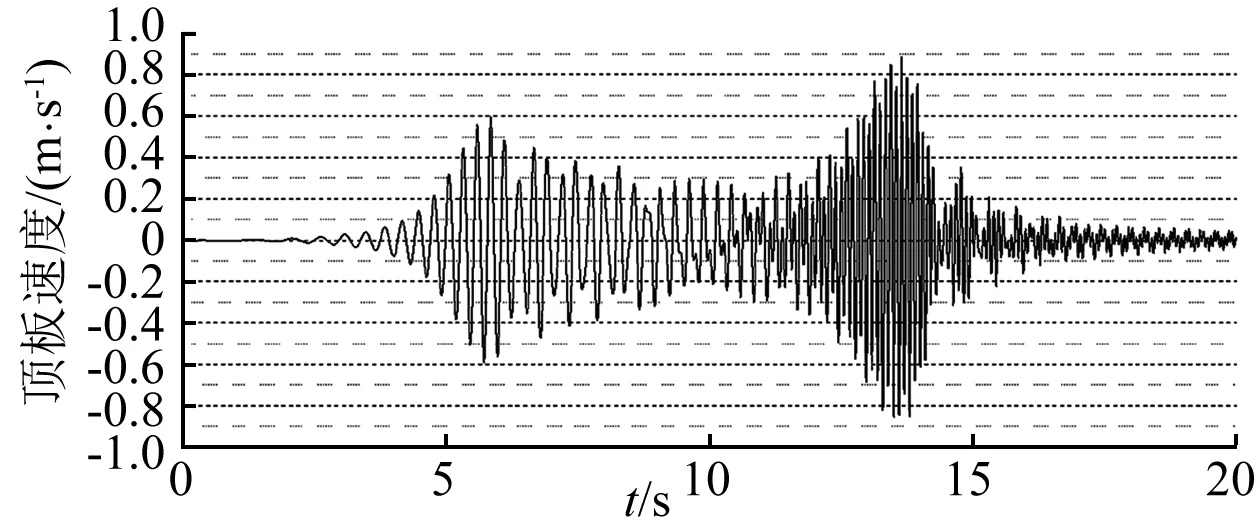
圖8 仿真得到框架頂層的速度時程Fig.8 Velocity time history at roof of the frame

3 NES振動控制的振動臺試驗

3.1 試驗對象與設備

試驗對象為一個小型二層鋼框架，框架詳細尺寸信息與“2.2”節中仿真對象的尺寸一致。經過掃頻測試，框架一階頻率為3.8 Hz、二階頻率為10.6 Hz。使用Shake Table II型振動臺，振動臺與框架的安裝狀態如圖9(a)所示。框架每層安裝一個IEPE型加速度計用來記錄框架動力反應信息，加速度信號經過信號調理后輸入數據采集卡。數據采集設備使用9125型16位四通道同步采集卡，試驗過程中采樣頻率200 Hz。

NES質量塊為一通過直線軸承在光軸上滑動的鋼塊，鋼塊兩側使用線性彈簧與框架的頂板連接，結構如圖9(b)所示。NES的質量與“2.2”節中計算取值一致，為130 g。張也馳等指出NES相對被控結構質量比≥5.6%是觸發最優靶向能量傳遞的條件，在試驗方案設計的時候考慮到在應用中NES的質量較輕的話利于實施，同時參考了結構振動中線性調頻質量阻尼器的質量比設定范圍，將其設定為一階模態質量的2.5%。該質量比雖然不能滿足動力學模型中最優的完全能量傳遞，但在試驗中還是發揮了較好的振動控制作用。

(a) 框架安裝在臺面上 (b) NES結構

3.2 試驗過程

振動臺臺面的輸入使用本文“2.2”節介紹過的Chirp信號，起始與截至頻率為1～15 Hz，幅值2 mm。在試驗中除了驗證仿真計算得到NES的彈簧剛度對試驗用框架加速度的控制，還改變NES彈簧的剛度試驗不同剛度對框架的振動控制效果的影響，所采用的彈簧見表1所列。另外為了考察NES對振動控制的魯棒性，在試驗過程中保持NES參數不變，改變框架的動力特性以考察其控制的寬頻特性。由于改變框架的剛度比較難，試驗中通過給框架頂板添加附加質量塊來改變框架的振動頻率。共有4個附加質量塊，每塊質量為0.4 kg，試驗過程中每次遞加一個，附加質量塊與框架的安裝見圖10。

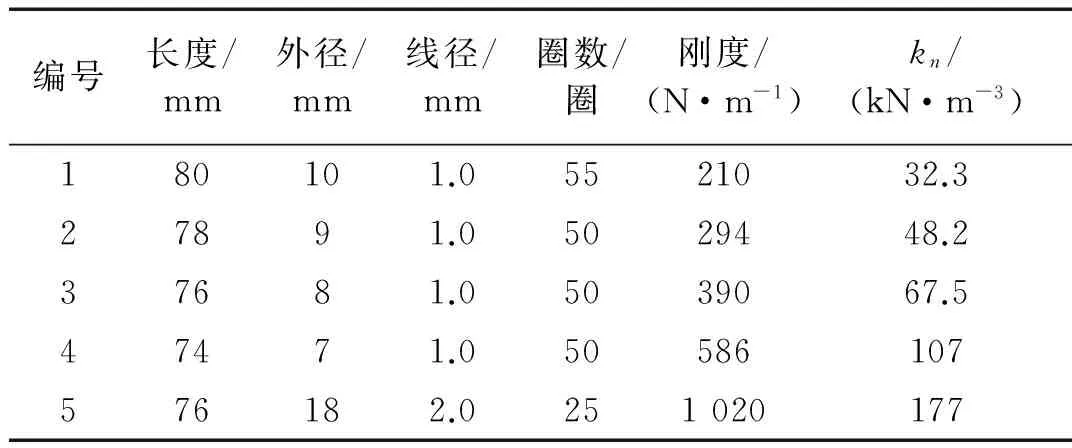
表1 試驗中使用的彈簧

圖10 附加質量塊Fig.10 Attached mass of the frame

3.3 試驗結果

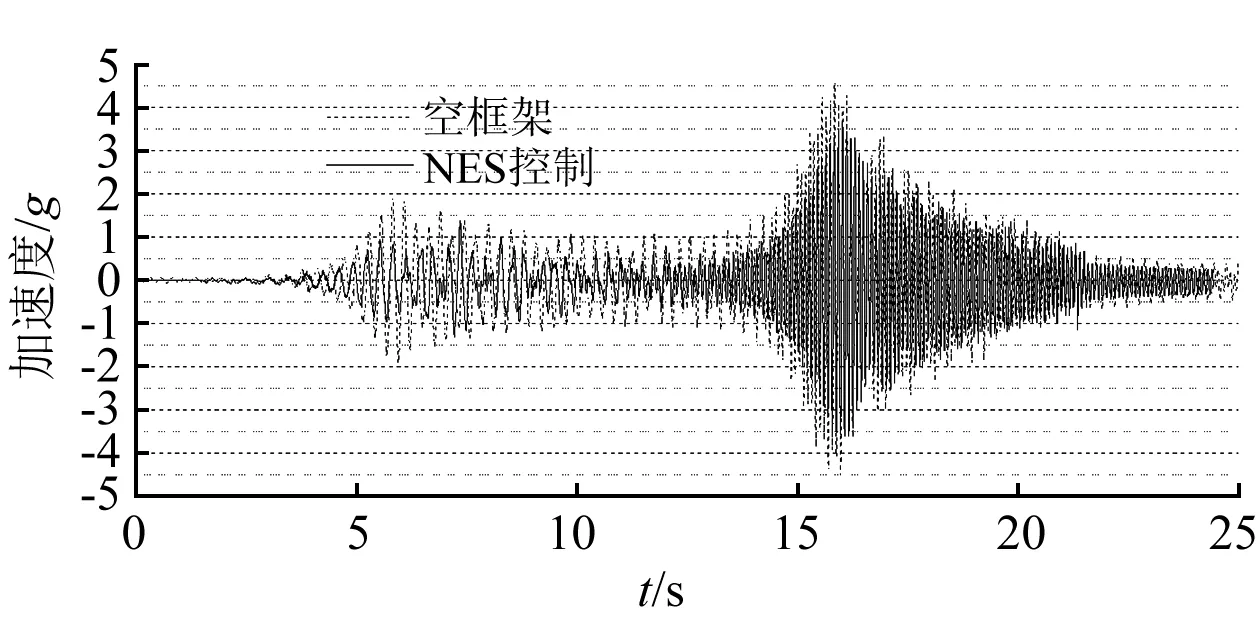
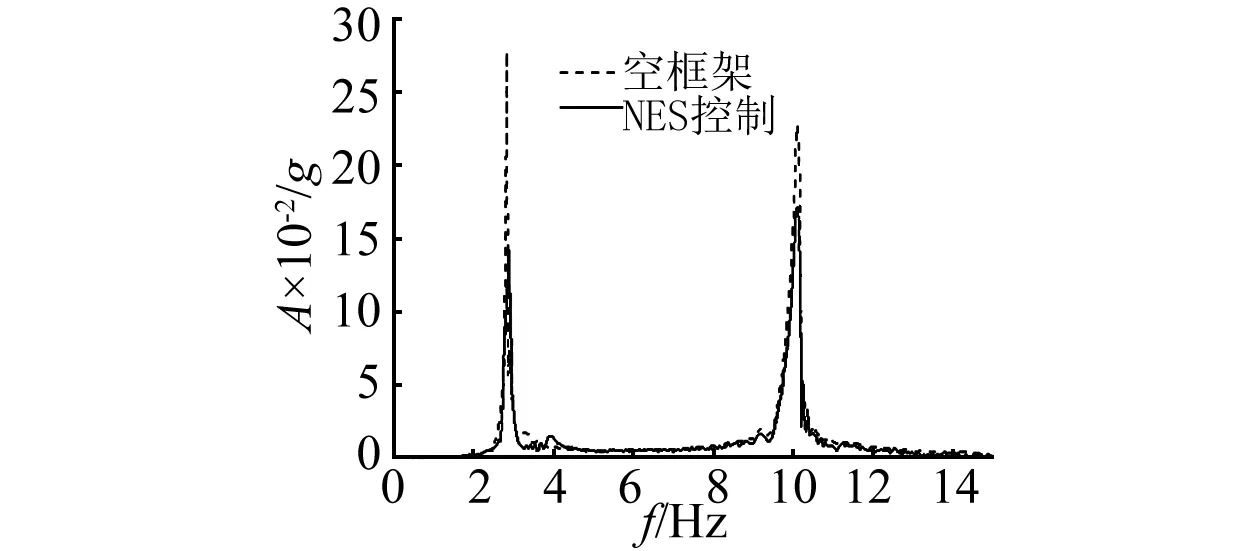
NES彈簧使用表1中編號1的彈簧來近似得到仿真計算中求得的較優剛度216 N/m，無附加質量空框架和NES控制下框架頂層加速度的時程與加速度響應譜對比分別如圖11(a)和圖11(b)所示。

(a) 框架頂層加速度時程對比

(b) 框架頂層加速度響應譜對比

由圖11(a)所示框架頂層加速度的時程曲線可以看出：在Chirp信號作用的起始階段的5～13 s內，振動臺臺面振動的頻率接近框架一階模態頻率。在該范圍內框架頂層的加速度得到了較好的控制，最大加速度由1.9g降低至0.79g。在13 s之后，振動臺加載的頻率接近框架的二階頻率，框架振動以二階頻率為主。此時從圖11(a)中加速度時程曲線可以觀察到，相對無控狀態，NES控制下框架頂層加速度雖然有一定量的削弱但是從加速度減小的比例上不如13 s之前。對兩個加速度時程分別計算其均方根，空框架的為0.913，NES控制下的為0.761相對空框架減少17%。

將頂層加速度時程數據進行FFT變換，轉到頻域范圍內進行分析，得到頂層加速度的反應譜如圖11(b)所示。從圖11(b)中可以觀察到一階頻率3.8 Hz下加速的響應譜幅值從0.39減小到0.11，降低了70%。二階頻率10.8 Hz下響應譜的幅值并無變化，這個與剛度優化計算中對一階模態振動控制的目標是一致的。另外在頂層加速度的時程曲線中，在振動臺激勵頻率接近框架二階模態頻率范圍內的時候，NES控制下的頂層加速度相對于無控下的也有減小，這種現象由頻域分析的結果可以得出結論：這個階段NES還是削弱振動中一階振動的部分。

表1中其他不同剛度的彈簧對試驗用框架振動控制的頻域效果對比如圖12所示,從圖中結果可以得到：①當NES使用比優化計算值大50%，剛度為300 N/m的彈簧時，響應譜中一階模態頻率的峰值為0.15g。與空框架的峰值0.39g相比還是降低了61%，這個試驗工況通過將彈簧剛度偏移優化值，對比空框架的動力響應，說明了NES對振動控制的寬頻特性。②隨著剛度的增加，NES對一階模態的振動控制開始減弱，對二階模態的振動控制開始加強。這個與剛度優化計算公式中所體現的隨著被控頻率的增加，需要同時增加NES剛度的關系是一致的。需要指出的是，雖然振動控制的效果在趨向二階模態振動控制的同時，一階模態的振動還是在一定程度上被削弱，這體現了NES的寬頻振動控制的優點。另外，由于Chirp信號激勵的特點，在接近二階頻率時候振動臺輸入的能量相對一階頻率時候要高，使得試驗框架頂板振動的速度值相對較大，同時在NES剛度優化計算中隨著被控結構能量水平越高反而需要相對低能量水平時更低的彈簧剛度。這樣造成了試驗中隨著彈簧剛度的增加，剛度越來越趨近較高速度條件下對頂板二階振動控制所需的較優的NES剛度，試驗中出現了對頂板二階振動控制效果開始明顯提升的現象。

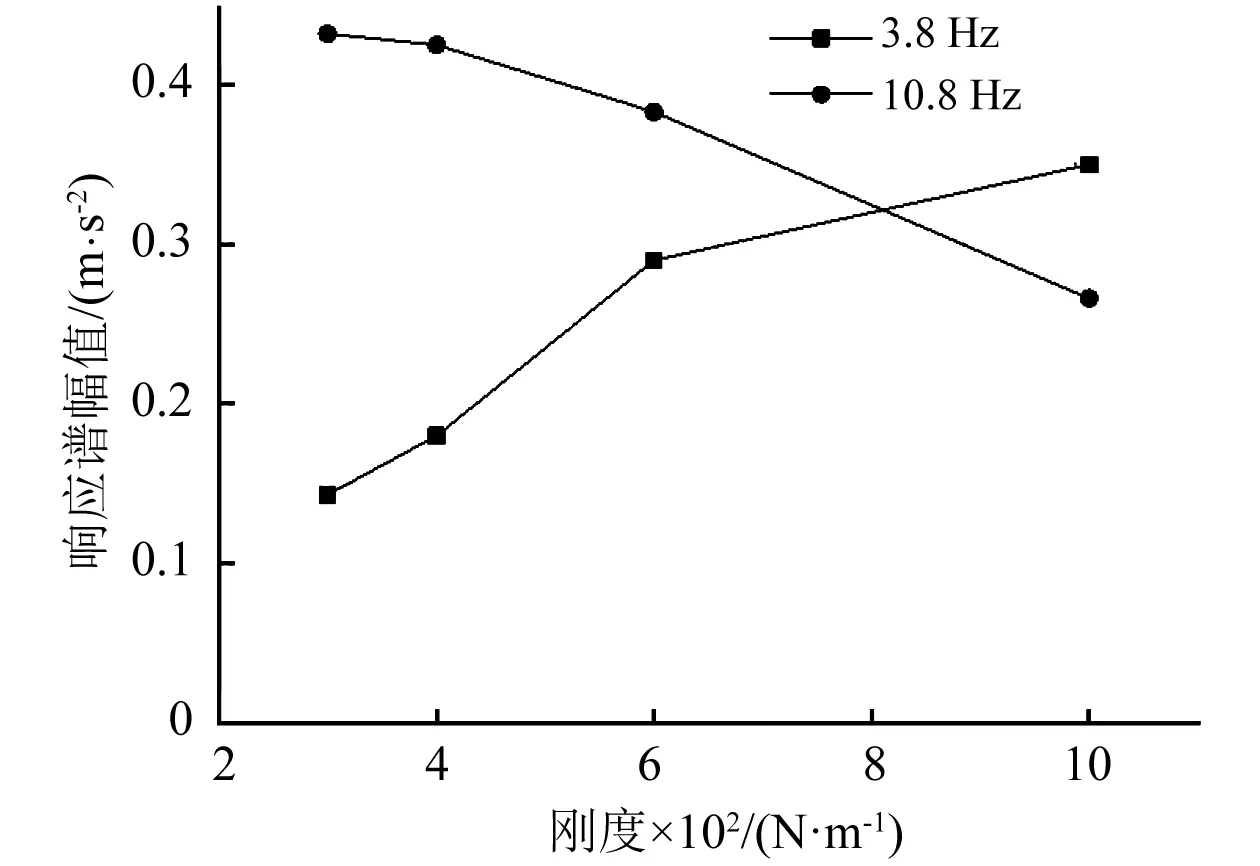
圖12 不同剛度彈簧控制效果對比Fig.12 Comparison of control effect between different stiffness of NES spring

在通過改變試驗框架的動力特性來考察NES寬頻控制效果試驗中，將4個質量塊同時附加在框架頂板上的時候，同時保持NES的質量130 g與剛度參數210 N/m不變。對附加質量的框架在無控與NES控制下分別進行試驗，外界激勵依然使用與之前試驗相同的Chirp信號，無控與有控下頂層加速度時程、響應譜對比分別見圖13(a)和圖13 (b)。對圖13(a)所示的兩個加速度時程分別統計其均方根，無控下為0.507，NES控制下為0.411相對無控下降低了19%。從圖13(b)可以觀察到，在給框架增加了1.6 kg的附加質量后一階頻率變為2.8 Hz。盡管一階頻率改變較大，但是從響應譜對比可以看出NES對框架的一階振動還是起到了較好的控制效果，將框架的一階頻率對應的加速度響應譜最大幅值從0.27降至0.15，減少44%。由于附加質量安裝在框架的頂部，框架的二階頻率改變并不大，僅降低為10 Hz，但是由于附加質量對框架振型的改變，NES對框架的二階振動也有了一定的控制效果，響應譜幅值從0.23降至0.17，減少26%。除此之外，從框架頂層的加速度時程可以看出，由于附加質量對框架的動力學特性做了較大的改變，頂板的加速度值也低于未附加的。在振動臺臺面激勵不變的前提下，可以判斷頂板的速度也低于未附加質量的框架。在該試驗工況中，相對剛度優化計算中設定的條件，兩方面較為顯著的不同：①框架動力學特性不同；②優化對象的速度不同。在這兩個實際條件顯著偏移優化計算設定的參數下，對比空框架與附加質量的框架分別在無控與有控下加速度的時域與頻域的對比結果，NES依然對一階振動有著較好的控制作用，可以說明NES在振動控制中有較高的魯棒性。

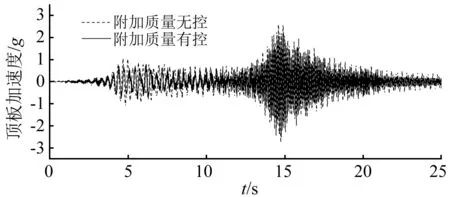
(a) 加速度時程

(b) 加速度響應譜

4 結 論

本文對被動式NES進行了研究，使用頻率能量圖說明了NES與線性振子連接到一起時候的動力學特性，介紹了一種解析的方式將單個NES剛度與多自由度線性振子能量水平、頻率、振型建立起關系，并依此關系對剛度進行優化計算的方法。

根據優化計算表達式與試驗對象的動力學特征，設計并開展了NES振動控制試驗，著重從頻域中考查NES的寬頻控制特性，從試驗結果得到如下結論：

(1)剛度優化計算公式是有效的，根據精確的參數進行優化計算得到的剛度來設計NES，可以有效控制優化計算中指定的目標模態振動，但是對其他模態振動并無明顯的控制作用。由于公式中體現了多自由度線性振子的振型、頻率和NES安裝位置，優化公式本身并不能體現NES寬頻控制的特性。

(2)對彈簧剛度改變試驗結果證明了NES的寬頻控制特性，在剛度超出優化計算值50%得時候，對目標模態振動的控制效果還較為明顯。這說明，在使用NES時候因其自身剛度參數精確度對控制效果造成負面影響的敏感性并不高，可以減少制作、實施的難度與工作量。

(3)改變試驗框架頂板質量的試驗結果同樣說明了NES的寬頻控制特性與魯棒性，在被控目標實際動力參數偏移計算參數范圍不大的情況下，NES依舊可以發揮振動控制作用。這使NES在類似精密設備機柜、運輸載具這類工作中質量常常不能精準確定，而又希望有消振措施的設備中有著良好應用場所。

目前關于NES在振動控制中的研究和應用還較少，考慮到其寬頻與較為魯棒的控制特性,這一類結構振動控制設備具有較大的研究與應用空間。

[ 1 ] ROBERSON R E. Synthesis of a nonlinear dynamic vibration absorber [J]. Journal of the Franklin Institute, 1952, 254(3): 205-220.

[ 2 ] VAKAKIS A F, GENDELMAN O. Energy pumping in nonlinear mechanical oscillators, Part Ⅱ: resonance capture [J]. Journal of Applied Mechanics, 2001, 68(1): 42-48.

[ 3 ] VAKAKIS A F. Inducing passive nonlinear energy sinks in vibrating systems [J]. Transactions-American Society of Mechanical Engineers Journal of Vibration and Acoustics, 2001, 123(3): 324-332.

[ 4 ] GOURDON E, LAMARQUE C H. Energy pumping with various nonlinear structures: numerical evidences [J].Nonlinear Dynamics, 2005, 40(3): 281-307.

[ 5 ] PANAGOPOULOS P N, VAKAKIS A F, TSAKIRTZIS S. Transient resonant interactions of finite linear chains with essentially nonlinear end attachments leading to passive energy pumping [J]. International Journal of Solids and Structures, 2004, 41(22): 6505-6528.

[ 6 ] GENDELMAN O, MANEVITCH L, VAKAKIS A F, et al. A degenerate bifurcation structure in the dynamics of coupled oscillators with essential stiffness nonlinearities [J]. Nonlinear Dynamics, 2003, 33(1): 1-10.

[ 7 ] LEE Y S, KERSCHEN G, VAKAKIS A F, et al. Complicated dynamics of a linear oscillator with a light, essentially nonlinear attachment [J]. Physica D Nonlinear Phenomena, 2005, 204(1):41-69.

[ 8 ] 張也弛,孔憲仁,楊正賢,等.非線性吸振器的靶能量傳遞及參數設計[J].振動工程學報,2011, 34(2):111-117. ZHANG Yechi, KONG Xianren, YANG Zhengxian, et al. Targeted energy transfer and parameter design of a nonlinear vibration absorber [J]. Journal of Vibration Engineering, 2011, 34(2):111-117.

[ 9 ] 張也弛,孔憲仁，張紅亮. 非線性耦合振子間的靶能量傳遞研究:保守系統中的完全能量傳遞[J].振動與沖擊,2012, 31(1):150-155. ZHANG Yechi, KONG Xianren, ZHANG Hongliang. Targeted energy transfer among coupled nonlinear oscillators:complete energy exchange in a conservative system [J]. Journal of Vibration and Shock, 2012, 31(1):150-155.

[10] 孔憲仁,張也弛.兩自由度非線性吸振器在簡諧激勵下的振動抑制[J].航空學報, 2012, 33(6):1020-1029. KONG Xianren, ZHANG Yechi. Vibration suppression of a two-degree-of-freedom nonlinear energy sink under harmonic excitation[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6):1020-1029.

[11] 陳勇，徐羿. 基于非線性能量吸振器的高聳結構減振分析[J].振動與沖擊,2014, 33(9):27-32. CHEN Yong, XU Yi. Vibration suppression analysis for a tall structure attached with a nonlinear energy sink absorber [J]. Journal of Vibration and Shock, 2014, 33(9):27-32.

[12] CARRELLA A, BRENNAN M J, WATERS T P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic [J]. Journal of Sound and Vibration, 2007, 301(3/4/5):678-689.

[13] KERSCHEN G, LEE Y S, VAKAKIS A F, et al. Irreversible passive energy transfer in coupled oscillators with essential nonlinearity [J]. SIAM Journal on Applied Mathematics, 2005, 66(2):648-679.

[14] MANEVITCH L, GOURDON E, LAMARQUE C H. Towards the design of an optimal energetic sink in a strongly inhomogeneous two degree of freedom system [J]. Journal of Applied Mechanics, 2007, 74(6):1078-1086.

[15] KERSCHEN G, PEETERS M, GOLINVAL J C, et al. Nonlinear normal modes, Part I: a useful framework for the structural dynamicist [J]. Mechanical Systems and Signal Processing, 2009, 23(1):170-194.

[16] PILIPCHUN V N. Transient mode localization in coupled strongly nonlinear exactly solvable oscillators [J]. Nonlinear Dynamics, 2008, 51(1): 245-258.

[17] GENDELMAN O, STAROSVETSKY Y, FELDMAN M. Attractors of harmonically forced linear oscillator with attached nonlinear energy sink I: description of response regimes [J]. Nonlinear Dynamics, 2008, 51(1/2):31-46.

[18] 熊懷,孔憲仁,劉源.阻尼對耦合非線性能量阱系統影響研究[J].振動與沖擊,2015, 34(11):116-121. XIONG Huai，KONG Xianren，LIU Yuan. Influence of structural damping on a system with nonlinear energy sinks [J]. Journal of Vibration and Shock, 2015, 34(11):116-121.

[19] VAURIGAUD B, SAVADKOOHI A T, LAMARQUE C H. Efficient targeted energy transfer with parallel nonlinear energy sinks: theory and experiment [J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(4):1-10.

Stiffness optimization and shaking table tests for nonlinear energy sink

LIU Zhongpo1, Lü Xilin2, WANG Dong2, WU Jianzhong1

(1.School of Mechanical Engineering, Tongji University, Shanghai 201804, China; 2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Nonlinear energy sink (NES) was proposed and its main feature to mitigate vibrations in a broad frequency band range was explored here. Firstly, the expressions for the relation between frequency and energy under 1∶1 resonance were derived using the analytical method. According to the expressions, the frequency-energy plot was drawn. This plot intuitively revealed that when a NES is attached to a linear oscillator, its vibration frequency relative to the linear oscillator has a direct relation to the energy level of the system. Then, the formulas for the relationships among the stiffness of NES and energy, frequencies and modal shapes of linear oscillators were derived with the analytical method in the model space of a multi-DOF vibration system. The optimal solution to NES stiffness was calculated with these formulas under a certain energy level of the vibration system. Based on the optimal stiffness calculation method, the NES vibration control test was designed and the corresponding shaking table tests were conducted. To test the wide frequency vibration control features of NES, a set of springs with different stiffness were employed and dynamic properties of the controlled frame were changed through adding the mass of the frame. The test results demonstrated that NES has a good broad frequency band vibration control effect, it can work well even though its stiffness deviates from the optimal value or there are some changes in dynamic features of the controlled target.

nonlinear energy sink; vibration control; shaking table test; nonlinear vibration

國家自然科學基金重大研究計劃重點國際合作項目(51261120377)；國家自然科學基金重大研究計劃集成項目(91315301-4)

2015-10-28 修改稿收到日期：2016-02-25

劉中坡 男，博士生，1980年生

呂西林 男，教授，博士生導師，1955年生

TB123；TU317.1

A

10.13465/j.cnki.jvs.2017.07.005