基于ASTFA和PMMFE的齒輪故障診斷方法

李寶慶　程軍圣　吳占濤　楊宇

摘要：提出一種新的反映信號復雜度或非線性度的方法——多尺度模糊熵偏均值（PMMFE），PMMFE是在多尺度模糊熵的基礎上提出的。多尺度模糊熵雖然包含不同尺度上的時間模式信息，反映了信號的內在特征，但是對于特征相近的信號，其在絕大部分尺度上的表征并不理想。PMMFE綜合考慮多個尺度的模糊熵值，利用不同尺度上模糊熵值的偏態分布特性來定量表征信號的復雜度或非線性度，更加準確地反映信號的特征。但是齒輪箱中的齒輪故障振動信號是多源振動信號，需將齒輪振動本源信號分離出來才能進行特征提取。自適應最稀疏時頻分析方法（ASTFA）根據齒輪嚙合頻率確定初始相位函數就可以有效分離齒輪故障振動本源信號。將ASTFA和PMMFE相結合用于齒輪故障診斷，首先采用ASTFA分離齒輪箱中的齒輪故障振動信號，其次計算該信號的多尺度模糊熵，再根據多尺度模糊熵計算PMMFE。實驗分析結果表明該方法能夠有效判別齒輪箱中的齒輪故障及其類型。

關鍵詞：故障診斷；自適應最稀疏時頻分析；齒輪；多尺度模糊熵；多尺度模糊熵偏均值

引言

基于振動的機械設備故障診斷的主要任務是從故障振動信號中提取故障特征信息，其中：準確分離故障振動信號是前提條件，提取故障特征信息是根本目的。工程上，齒輪傳動一般以齒輪箱的形式存在，當齒輪發生故障時，其故障振動信號在齒輪箱內任意傳遞。而在進行振動信號采集時，由于傳感器一般安裝于箱體上，因此采集到的齒輪故障振動信號極易受到傳遞路徑上的主軸、滾動軸承等元件及其噪聲的干擾，最終采集得到的振動加速度信號包含了多重振源。從而，對于齒輪故障診斷來講，首先需采用合適的信號處理方法將齒輪故障振動的本源信號分離出來，然后再對分離后的信號進行故障特征提取。

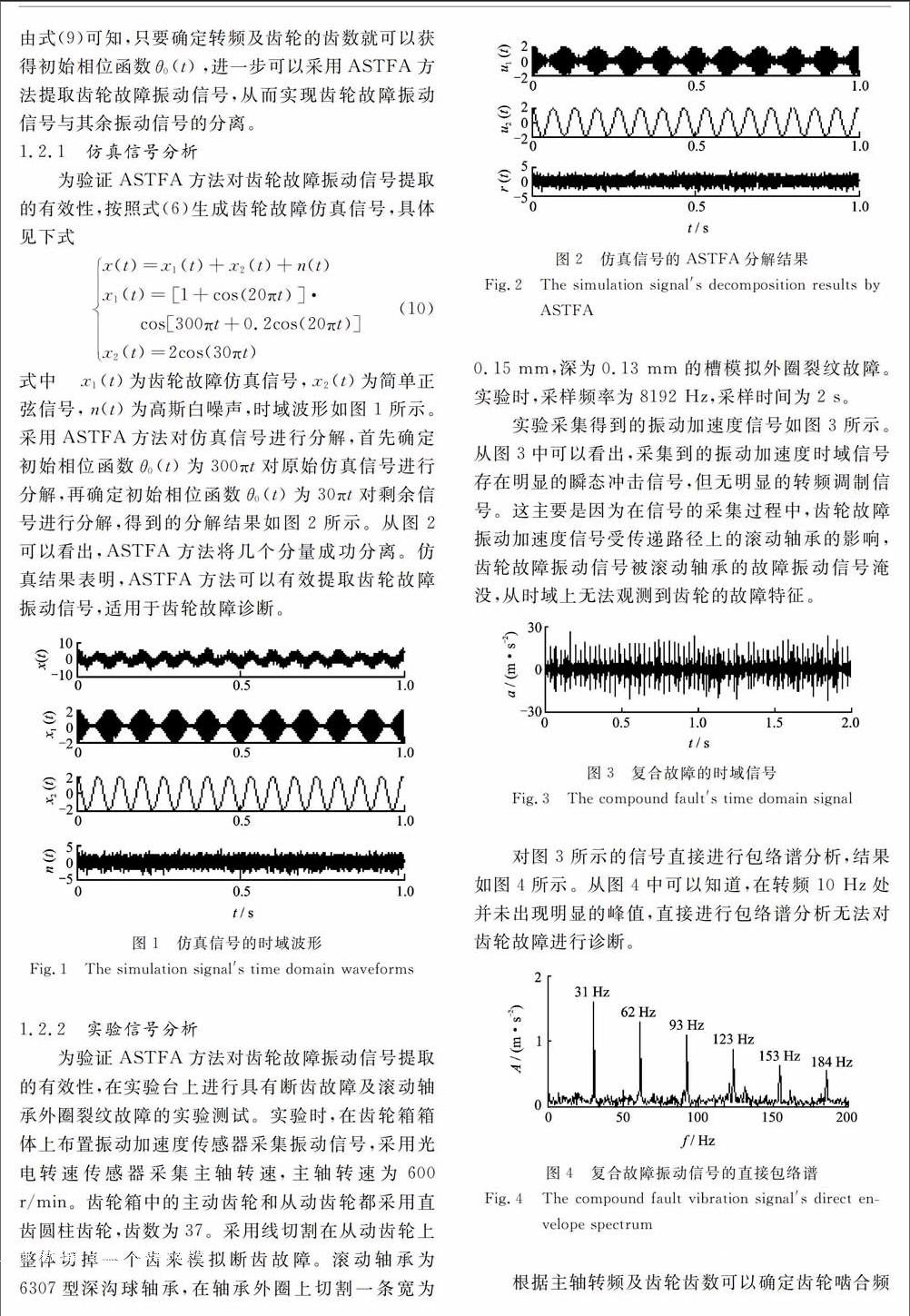
對于齒輪故障振動本源信號的分離，目前主要使用的方法有：總體平均經驗模態分解（Ensemble Empirical Mode Decomposition，EEMD）、形態分量分析（Morphological component Analysis，MCA）、盲源分離等。但是這些方法都存在一定的問題，EEMD方法的計算量大，添加的白噪聲不能被完全中和，分解結果的偽分量較多；MCA方法過分依賴于合適的字典庫，自適應性下降，另外小波系數閥值的選取對MCA方法的分解效果有很大的影響，而且閥值的選擇存在難度且具有較強的主觀性；盲源分離方法具有多解性，得到的分離信號具有不確定性，尤其是為保證正定性，需對源信號的個數進行估計，但目前的一些方法在估計結果的準確性上還存在欠缺。受壓縮感知理論（compressive Sensing，CS）及EMD方法的啟發，THOMAS Y HOU和Zuoqiang SHI于2011年提出了ASTFA方法，主要思想是通過尋找原信號的最稀疏表示將信號分解問題轉化為非線性優化問題，通過解決非線性優化問題實現信號的分解。AsTFA分解信號時，相位函數優先滿足收斂要求，則所對應的信號優先分解。當齒輪發生故障時，其故障振動信號的載波相位函數由嚙合頻率決定且滿足AsTFA的收斂要求，因此可采用ASTFA實現齒輪故障振動本源信號的分離。

對于故障特征的提取，由于齒輪故障振動信號具有非平穩、非線性特征，而熵是一種有效的表征時間序列復雜性的非線性動力學方法，因此可用熵來表示齒輪故障特征。模糊熵是在樣本熵的基礎上發展的一種衡量時間序列復雜性的方法，已廣泛應用于機械設備故障診斷。為更加有效地表征故障特征，文獻在模糊熵的基礎上引入尺度因子，提出了多尺度模糊熵（Multi-scale Fuzzy Entropy，MFE），但是多尺度模糊熵無法準確分辨故障特征較為相近的不同類型故障。文獻的研究指出，綜合考慮多個尺度上的熵值可以更準確地衡量時間序列的復雜性。因此本文綜合考慮多個尺度的模糊熵值，在多尺度模糊熵的基礎上提出多尺度模糊熵偏均值（Partial Mean MFE，PMMFE）。多尺度模糊熵偏均值相比多尺度模糊熵可以更準確地分辨特征相近的不同類型故障。

本文結合ASTFA和多尺度模糊熵偏均值的優點，提出基于ASTFA和多尺度模糊熵偏均值的齒輪故障診斷方法，首先采用ASTFA將齒輪箱中的齒輪故障振動本源信號分離出來，其次計算分離信號的多尺度模糊熵，再根據多尺度模糊熵計算多尺度模糊熵偏均值，通過多尺度模糊熵偏均值來表征不同類型的齒輪故障。實驗分析結果表明基于ASTFA和多尺度模糊熵偏均值的故障診斷方法能夠有效判別齒輪箱中的齒輪故障及其類型。