一階連續(xù)可微復(fù)值函數(shù)的開映射定理

董新漢，劉宗盛

(湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，中國(guó) 長(zhǎng)沙 410081)

一階連續(xù)可微復(fù)值函數(shù)的開映射定理

董新漢，劉宗盛

(湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，中國(guó) 長(zhǎng)沙 410081)

將解析函數(shù)的保區(qū)域定理、最大模定理和惟一性定理推廣至一階連續(xù)可微的復(fù)值函數(shù).并進(jìn)一步將其拓展到高維空間.對(duì)解析函數(shù)根點(diǎn)的重?cái)?shù)、曲線的index和拓?fù)涠冗M(jìn)行了討論和展望.

保區(qū)域定理；最大模定理；惟一性定理

在普通本科院校數(shù)學(xué)系的復(fù)變函數(shù)教材里[1-4]，介紹了解析函數(shù)f的保域性定理，即f是一個(gè)開映射.這個(gè)性質(zhì)隱含解析函數(shù)的最大模定理.圍繞該定理的研究很多[5-7]，但大都超越本科生的知識(shí)范圍.本文僅在數(shù)學(xué)分析的水平上給出一個(gè)推廣，因此本科生亦可接受.通過推廣這個(gè)定理，可加深對(duì)隱函數(shù)存在定理、二元函數(shù)極值定理有關(guān)知識(shí)的學(xué)習(xí).在此基礎(chǔ)上通過延伸討論，可開拓視野.先介紹簡(jiǎn)單而特殊的情形.

1 保域性定理與最大模定理

定理1(保域性定理) 設(shè)Ω?是一個(gè)區(qū)域，f(z)=φ(x,y)+iψ(x,y)∈C1(Ω)且判別點(diǎn)集(或奇點(diǎn)集)Z={z:Jf(z)=0}是Ω中的離散集，其中是Jacobi行列式，則f(Ω)是一區(qū)域.

注 應(yīng)該注意，非常數(shù)的解析函數(shù)f,它的判別點(diǎn)集(或奇點(diǎn)集)Z={z:Jf(z)=0}是一離散集.在定理1中，Z={z:Jf(z)=0}是Ω中的離散集的條件是不可去掉的，例如f(x,y)=u(x,y)+ic,其像落在水平線v=c上.

由于區(qū)域是連通的開集，并且連通集的連續(xù)像是連通的，那么對(duì)定理1只需要證明f(Ω)是一開集，這個(gè)證明由引理1和引理2構(gòu)成.為此首先證明:

引理1 設(shè)Ω?是一個(gè)區(qū)域，f(z)=φ(x,y)+iψ(x,y)∈C1(Ω).如果z0∈Ω,w0=f(z0)=u0+iv0,Jf(z0)≠0,則存在ρ>0使得C(w0,ρ)?f(Ω).

證 設(shè)z0=x0+iy0,P0=(u0,v0,x0,y0),a=φx(x0,y0),b=φy(x0,y0),c=ψx(x0,y0),d=ψy(x0,y0).考慮

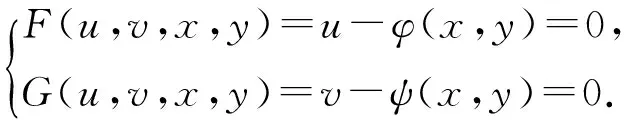
由隱含數(shù)存在定理，在P0的某鄰域D?×Ω內(nèi)由F=0，G=0確定唯一一組函數(shù)

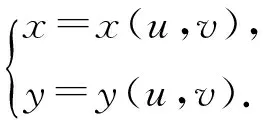
它們被定義在w0=u0+iv0的某鄰域C(w0,ρ)內(nèi)，有連續(xù)偏導(dǎo)數(shù)且x0=x(u0,v0),y0=y(u0,v0),(x0,y0)∈Ω.我們可選ρ>0很小，使得在C(w0,ρ)上通過上述方程組定義的(x,y)所對(duì)應(yīng)的值域E?Ω.此表明f(E)=C(w0,ρ)?f(Ω).

引理2 設(shè)Ω?是一個(gè)區(qū)域，f(z)=φ(x,y)+iψ(x,y)∈C1(Ω),Z={z:Jf(z)=0}是Ω中的離散集.若z0∈Ω滿足Jf(z0)=0,則存在ρ>0使得C(w0,ρ)?f(Ω),其中w0=f(z0).

證 因?yàn)閆是離散的，我們可找δ>0滿足

(1)

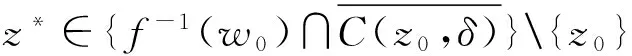
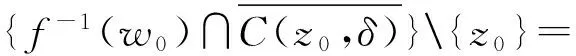
{f(0<|z-z0|≤δ)}∩{f(z0)}=?.

(2)

由(1)和引理1，我們知道D:={f(0<|z-z0|<δ)}是一連通開集，因此是一連通區(qū)域.由f的連續(xù)性和(2)，D的邊界點(diǎn)落在{w0}∪{f(|z-z0|=δ)}上，則w0=f(z0)必須是D的孤立邊界點(diǎn)，因此D∪{w0}是一區(qū)域.此表明存在ρ>0使得C(w0,ρ)?f(Ω).

由引理1和引理2得到定理1.由定理1立即得到

定理2(最大模定理) 設(shè)Ω?是一個(gè)區(qū)域，f(z)=φ(x,y)+iψ(x,y)∈C1(Ω)且Z={z:Jf(z)=0}是Ω中的離散集，則|f(z)|在Ω內(nèi)不能達(dá)到最大.

由上面的證明可知，以上結(jié)論完全可推廣到高維空間.

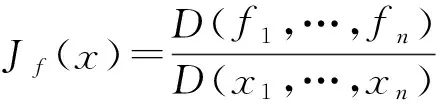
2 零點(diǎn)的孤立性定理

下面在定理1的條件下，介紹零點(diǎn)的孤立性定理.該定理的證明可利用引理1的隱函數(shù)定理的局部同胚性質(zhì)直接得到，若有意使用下面的證明，它與數(shù)學(xué)分析二元函數(shù)極值的判定定理的證明相同.

定理4(零點(diǎn)的孤立性定理) 設(shè)Ω?是一個(gè)區(qū)域，w=f(z)=φ(x,y)+iψ(x,y)∈C1(Ω),z0∈Ω,Jf(z0)≠0,則存在δ0>0使得f(z)-f(z0)在0<|z-z0|≤δ0內(nèi)沒有零點(diǎn).

證 設(shè)a=φx(x0,y0),b=φy(x0,y0),c=ψx(x0,y0),d=ψy(x0,y0),有

Jf(z0)=ad-bc≠0.

(3)

由一階連續(xù)可微條件可得到

f(z)-f(z0)=(a+o(1))(x-x0)+(b+o(1))(y-y0)+

i((c+o(1))(x-x0)+(d+o(1))(y-y0))=

(a+ic)(x-x0)+(b+id)(y-y0)+o(1).

假設(shè)x-x0=ρcosθ,y-y0-ρsinθ,上式可以簡(jiǎn)化為

f(z)-f(z0)=ρ(h(θ)+o(1)),

(4)

這里h(θ)=acosθ+bsinθ+i(ccosθ+dsinθ)和

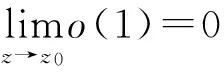
(5)

注意到

|h(θ)|2=(acosθ+bsinθ)2+(ccosθ+dsinθ)2=

(a2+c2)cos2θ+(b2+d2)sin2θ+2(ab+cd)cosθsinθ.

觀察實(shí)對(duì)稱二次型F(x,y)=(a2+c2)x2+(b2+d2)y2+2(ab+cd)xy,由(3)可知它的順序主子式P1=a2+c2>0和

P2=(a2+c2)(b2+d2)-(ab+cd)2=(ad-bc)2=|Jf(z0)|2>0,

因此F(x,y)是正定二次型.設(shè)m=minθF(cosθ,sinθ)=min|z|=1F(z)=minθ|h(θ)|2.由正定性有m>0.由(4)和(5)，得到存在δ0>0使得當(dāng)0<|z-z0|=ρ≤δ0時(shí)

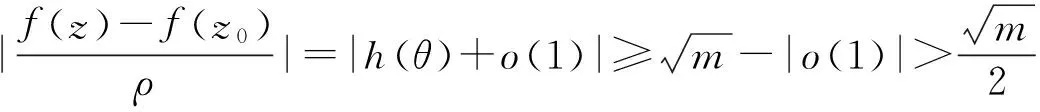
因此f(z)-f(z0)在0<|z-z0|≤δ0內(nèi)沒有零點(diǎn).

毫無疑問，上面的定理也可以推廣到高維空間.

3 零點(diǎn)重?cái)?shù)及有關(guān)展望

當(dāng)Jf(z0)=0時(shí)，在C1的情形下我們沒有函數(shù)的太勒展開，因此沒有m階零點(diǎn)和根點(diǎn)的重?cái)?shù)概念.為了定義重?cái)?shù)，需要引入新的概念，例如引入degree或曲線的index等概念[8-13]，這樣可將研究對(duì)象進(jìn)一步拓展到連續(xù)函數(shù)，這方面的研究將另文展開，本文不涉及.下面證明一個(gè)有限重?cái)?shù)的結(jié)論，先要引進(jìn)一個(gè)概念.

定義[8]假設(shè)X和Y是兩個(gè)拓?fù)淇臻g，f是X→Y的連續(xù)映照，對(duì)每個(gè)緊集E?Y,均有f-1(E)也是緊的，則稱f是逆緊映射(proper mapping).

命題1 設(shè)Ω?是一個(gè)區(qū)域，f(z)=φ(x,y)+iψ(x,y)∈C1(Ω)是逆緊的.設(shè)Z={z:Jf(z)=0}和w0?f(Z),則f-1(w0)是一有限點(diǎn)集.

證 由逆緊的定義，f-1(w0)是一緊集.任取z∈f-1(w0),則z?Z.再由定理1知，存在δz>0滿足|f(ξ)-w0|>0,0<|ξ-z|<δz.換言之{ξ:0<|ξ-z|<δz}∩f-1(w0)=?.因此f-1(w0)是一離散緊集，而離散緊集必須是一有限集.

對(duì)于解析函數(shù)，有以下關(guān)于零點(diǎn)重?cái)?shù)的定理.

定理A[14-15]設(shè)Ω,G是復(fù)平面上的區(qū)域，f是Ω到G的全純逆緊映射(analytic proper mapping),則存在正整數(shù)k(稱degree)滿足nf(w,Ω)≡k,?w∈G,這里nf(w,Ω)表示方程f(z)=w在Ω內(nèi)根的個(gè)數(shù)(計(jì)重?cái)?shù)).

將定理A進(jìn)行推廣，去掉逆緊的概念，得到如下的定理B.

定理B[11-12]設(shè)f在Ω?上解析且連續(xù)到邊界，假設(shè)f(Ω)f(?Ω)=∪i≥0Wi是連通分支分解.則存在正整數(shù)ki使得nf(w,Ω)≡ki,?w∈Wi.

注 在定理B中，存在一個(gè)極端的情況[16]，即存在f滿足f(Ω)f(?Ω)=?.

Riemann-Hurwitz公式[15，17]設(shè)Ω是W復(fù)平面上的區(qū)域，它們的連通數(shù)分別是c(Ω),c(W)<∞.又設(shè)f是Ω到W的全純逆緊映射具有W=f(Ω),設(shè)f的degree為k,奇點(diǎn)集Z={z:f′(z)=0}的個(gè)數(shù)為v(按重?cái)?shù)計(jì))，則c(Ω)-2=k(c(W)-2)+v.

在C1條件下可以推廣根點(diǎn)的重?cái)?shù)的定義[13]，此時(shí)可以考慮上面的定理B以及Riemann-Hurwitz公式.這些是很有研究?jī)r(jià)值的問題.

[1] 鐘玉泉.復(fù)變函數(shù)論[M].北京：高等教育出版社，2004.

[2] 獲利莉，何成奇.復(fù)變函數(shù)論[M].上海：上海科學(xué)技術(shù)出版社，1987.

[3] 鄭建華.復(fù)變函數(shù)[M].北京：清華大學(xué)出版社，2005.

[4] 庹克平，李鳳友.函數(shù)方法論[M].天津：天津大學(xué)出版亮度，1980.

[5] 董新漢，伍海華.關(guān)于多值解析函數(shù)的教學(xué)研究[J].大學(xué)數(shù)學(xué), 2013,29(1):87-91.

[6] 伍海華，董新漢.單位圓盤上全純逆緊映射的像區(qū)域[J].湖南師范大學(xué)自然科學(xué)學(xué)報(bào), 2009,32(4):7-9.

[7] 董新漢.關(guān)于De Branges定理的一個(gè)注記[J].湖南師范大學(xué)自然科學(xué)學(xué)報(bào), 1991,14(3):193-197.

[8] BEARDON A F. Complex analysis:the argument principle in analysis and topology[M].Chichester: John Wiley, 1979.

[9] DONG X H, LAU K S. Cauchy transforms of self-similar measures: the Laurent coefficients[J]. J Funct Anal, 2003,202(1):67-97.

[10] DONG X H, LAU K S. An integral related to the Cauchy transform on the Sierpinski gasket[J]. Exp Math, 2004,13(4):415-419.

[11] DONG X H, LAU K S. Cantor boundary behavior of analytic functions. Recent Development in Fractals and Relatd Fields[M]. New York: Springer-Verlag, 2010.

[12] DONG X H, LAU K S, LIU J C. Cantor boundary behavior of analytic functions[J]. Adv Math, 2013,232(2):543-570.

[13] TEMME N M. Nonlinear analysis[M]. Amsterdam: Mathematisch Centrum, 1976.

[14] RUDIN W. Function theory in the unit ball ofn[M]. New York: Springer-Verlag, 1980.

[15] TEINMETZ N S. The formula of Riemann-Hurwitz and iteration of rational functions[J]. Complex Variables Theory Appl, 1993,22(2):203-206.

[16] CHURCH P. Boundary image of Meromorphic fucntions[J]. Trans Amer Math Soc, 1964,110(1):52-78.

[17] BEARDON A F. Iteration of rational functions, complex analytic dynamical systems[M]. New York: Springer-Verlag, 1991.

(編輯 CXM)

On Open Mapping Theorem of Complex Valued Functions withC1Condition

DONGXin-han,LIUZong-sheng*

(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

The open mapping theorem, the maximum modulus theorem and the uniqueness theorem are generalized from analytic functions to complex valued functions withC1condition. Furthermore, the same results in high-dimensional space are established, the applications of the multiplicity of root, index and degree are discussed.

open mapping theorem; maximum modulus theorem; uniqueness theorem

10.7612/j.issn.1000-2537.2017.02.013

2016-11-14

國(guó)家自然科學(xué)基金資助項(xiàng)目(11571099);高等學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金資助項(xiàng)目(20134306110003);湖南省教育廳教改項(xiàng)目(湘教通[2010]243號(hào))和科研資助項(xiàng)目(14K057)

G420；O174.5

A

1000-2537(2017)02-0081-04

*通訊作者,E-mail：lzsheng1992@163.com