深度挖掘
——新的統計方法幫助人們更有效地了解過程、建立模型

深度挖掘
——新的統計方法幫助人們更有效地了解過程、建立模型

編者按

一種新的統計方法可用來研究過程，即觀察、檢查、分配、回歸和自然選擇法（5個單詞的首字母縮寫為LEARN）；該方法結合了成熟的工具，在不需要高等數學的情況下，能夠打造強大而且簡單的模型；LEARN方法可以通過查找和應用增值信息將數據結構化為線性擬合。這種新的統計方法幫助人們“深度挖掘”。

隨著對數據的日益重視以及數據實用性的提高，人們對有意義的且可用的分析充滿了更多期待。如今的決策者越來越需要從所有的數據中提取價值。單個系統及多個系統中的過程都應被清晰地描述，并易于理解，從而實現回歸分析，并對來自穩定過程的歷史行為進行建模，從而最好地預測未來的績效表現。

有了如此多的現成數據，我們可能會產生錯覺，認為所有準確的數據都唾手可得。可一旦預測變量和響應變量之間幾乎沒有任何關系，或數據缺乏重要參數時，都會使數據決策者對模型的預測能力包括主觀評價感到不滿意或不解。

這樣的情景聽起來是不是感到很耳熟？你的老板有理由不接受這樣的分析。他期待一個簡單有用的模型來提供對未來績效的洞察和分析，但得到的卻是一個輸入與輸出之間缺乏足夠相關性的回歸分析。這就意味著預測能力值得懷疑，因此他對未來的分析也就會更多地包含警告而不是聲明。

“你讓我拿這些數據怎么辦？這也不比使用平均值好多少啊。”老板如此尖刻的批評迫使分析師又加入了更多輸入，以此提高模型的可決系數。幾番來回，在一段緊張的日子后，模型最終演化成了復雜而繁瑣的東西，充滿了高階、非線性和多重共線性。

當你解釋邏輯回歸時，老板的眼睛只會呆滯地轉上兩分鐘。這并不是說高階、非線性或邏輯回歸的方法不好，而是這些東西出現的時間和地點不對。它們會讓人備受打擊。雖然分析師制作了詳盡的、由現有數據支撐的統計評估，但老板要求的卻更多。分析師的內心在暗暗尖叫，“如果我能做得更好，那我早就做了！”

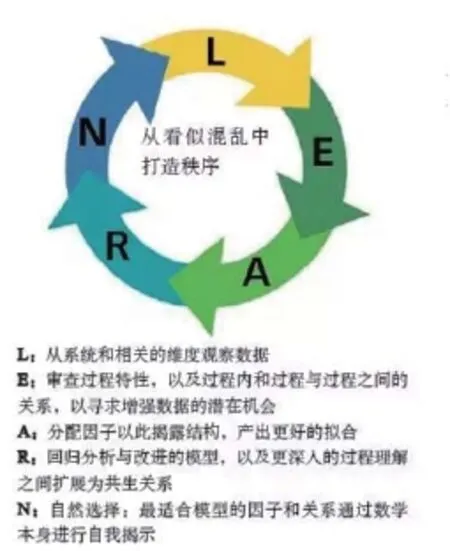
圖1 LEARN方法

數據信息越好，分析成功的程度也會越高。即使高等統計的數據也是與表示過程的數據相關聯的。幸運的是，穩定的過程通常已包含有助于減少變異的特性。

如圖1所示，觀察、檢查、分配、回歸和自然選擇法（LEARN方法）與經過驗證的工具相結合，能夠產生出功能強大而簡單的模型，而無需高等數學。通過制定更豐富的輸入產生分析輸出，LEARN方法可以幫助你滿足老板不斷增長的期望。那些擁有大量數據、數據易于獲得、范圍較嚴格的項目（如優化機器設置），最好運用DMAIC方法（即定義、測量、分析、改進和控制），以及可靠而直接的六西格瑪方法。

但不幸的是，通常只有當領導們表示出對模型的不滿意且沒有其他可用數據能讓一切好起來時，回歸分析才會暴露出數據的種種局限。LEARN方法可被當作事后的補充方法，以充實現有的信息。

在過程中應用LEARN方法。例如，某公司副總裁負責監管11個部門，而且要為一個新的項目估算人工小時數。員工雖有一些流失，但基本沒有太大損耗，所以她的組織在過去5年里相當穩定。根據圖2中的評估，她得出結論：她需要更好的預測性。

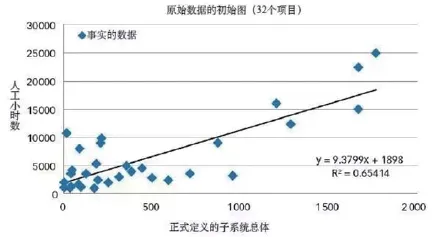
圖2 初始圖缺少期待的可預測性

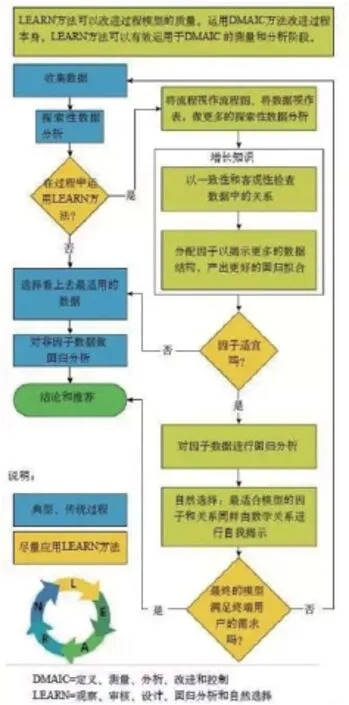
圖3 將LEARN方法與傳統過程流融合

她認為模型總的來說和數據匹配，但她懷疑所在組織（也稱為過程或系統）不可預測。其實，她所在組織可能并不是真的不可預測，而是選出來代表組織的數據不可預測罷了。

雖然副總裁估算的必要精度已經超出了圖2的能力范圍，但數據就是數據。圖3延伸了選擇數據、分析流程的傳統，而將LEARN方法引入其中。圖3最終可能會倒退到初始評估。本文的其余部分將會通過圖3來假設數據的不足。

LEARN方法的目的是產生足夠多的數據（甚至可能比足夠還要多），以消除投機或編造的信息，并進一步地剖析數據，以揭示更深的過程特性。

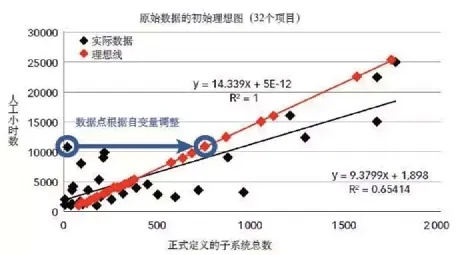
圖4 一個可能實現的理想擬合圖

從全新視角進行觀察

觀察階段始于定位合適的主題專家（SME），而不是單個分析者，以此來豐富擴充信息、用于額外的分析。主題專家為初步的統計評估增加了系統工程要素。

最適合支持LEARN方法的主題專家通常是熟悉系統級交互的高層人員以及老練的流程負責人。專家團隊通過系統地組合數據，或更常見地分解現有數據來豐富信息。我們希望團隊能夠順利走過團隊融合及會議管理的各個階段，即形成期、震蕩期、規范期和執行成長期，還希望多學科的主題專家們能在過程中相互理解、互相幫助、成長共生。

觀察階段的任務是全面了解與過程相關的過程和數據。這種了解使我們能夠對數據輸入的要素進行后續討論，從而對過程產生更加深入的理解。而且比起當前的輸入，這樣的做法會為模型帶來更多價值。

觀察階段首先是繪制流程圖，簡單組織初始的數據，如表1中的前兩列數據，并以團隊的形式對數據進行討論。這些數據本身并不能提供回歸分析以外的潛力，這遠遠低于副總裁的既定目標。這些數據所創造出的是以事實為基礎的分析，但卻不能用來進行創造性的推測。

系統地討論現有數據，如它如何反映過程、過程如何產生數據以及過程為什么會產生其所產生的數據。了解表格中的關系：行內的信息表示系統內的行為，而列內的信息表示系統間的行為。通過查看散點圖、箱線圖和帕累托圖來繼續對數據進行探索，還可以開展更簡單的線性回歸，以此涵蓋不同的變量并挑選出其中最好的變量。以上所有活動都要以團隊的形式進行展開，團隊應該在觀察階段結束前做好充分準備，以討論增強數據的各種方法。

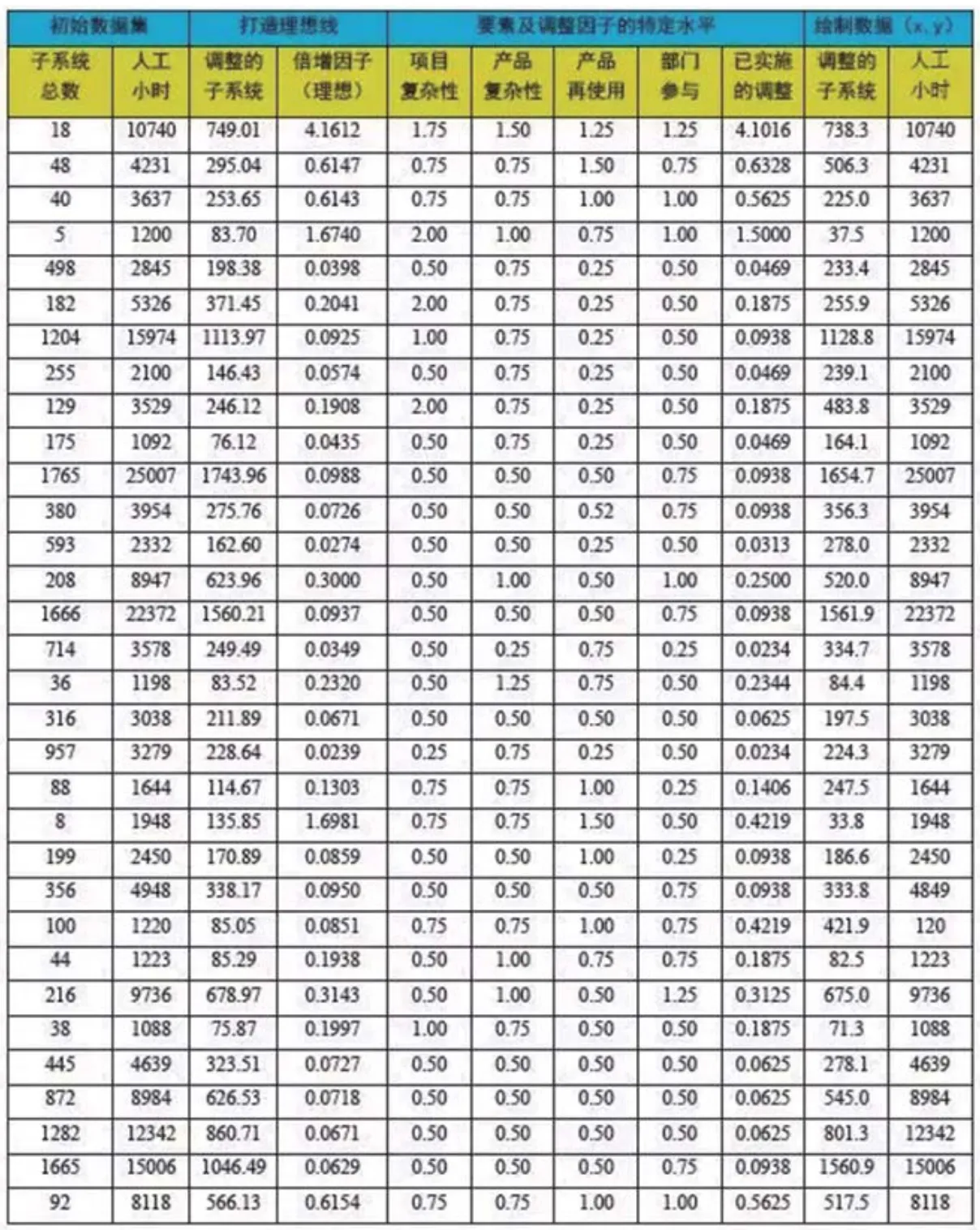
表1 案例中的關鍵數據

檢查過程，而不僅僅是數據這個階段的任務是從混亂中創造秩序。現在團隊已經開始熟悉起來，并做好了進一步描述過程特點的準備，在此過程中他們很可能經歷震蕩階段。

在初始數據集里，改進模型所必需的特性很不明顯。如果明顯的話，它們會被用于原始分析。通過在觀察階段用心地應用獲得的知識，這些特征得以展示或被進一步加工。檢查階段有兩個主要目標：

1.計算產生理想回歸線所需的每個初始數據點的倍增因子（即R2=1）。原始數據顯示在表2的第3和第4列中。圖4將R2=1作為改進模型的起點。這個理想圖并不是最終目的。它既不是預定義的，也不是具體的，而僅僅是模型開始演變的總體方向。

2.我們要確定使數據點指向理想線的過程特性，同時不損害對過程或模型的完整理解。這個過程并不是要對一些對過程毫無意義的數據產生幻覺，誤以為模型良好而有活力，而是要揭開合理的特性，特別是穩定過程的特性，從而減少數據點與理想曲線之間的差距。

過程特性通常包括獨立變量。這意味著沿x軸的調整，如圖4所示，這種做法非常有意義。因為表1中的人工小時數是具體的，而預測變量（即總數內部的影響關系）是不確定的，需要更多細節來解釋范圍和水平上的細微差別。

通過進一步找出x軸上獨立變量的特性來產出理想圖，還需要額外的數學步驟，因為斜率是由Δx/ Δy來決定。從傳統的點斜率公式開始入手：將截距排除不計，由此產生理想模型的方程式為強制截距通過原點，需要正當的理由，應證明如下：

?截距項在理想圖的回歸分析中不顯著。

?理想圖對零刺激的響應為零。

國有林場半專業化勞務派遣森林消防隊是國有林場撲救森林火災的應急補充力量，是縣、鄉專業森林消防隊伍的得力助手。在今后的工作中，要進一步探索國有林場半專業化勞務派遣森林消防隊建設管理新路子，從人員管理、培訓教育、制度建設、物資保障、實戰考核等方面入手，強化組織管理，建設一支素質高效，作風過硬，紀律嚴明，英勇善戰，在撲救森林火災中起到重要作用的新型國有林場半專業化森林消防隊伍。

?斜率在所有點都相同。

將表2里的總子系統設為y，人工小時數設為x，則Δx/Δy為0.06974。項目1的理想點為：

然后，計算每個項目理想的倍增因子：

其中分母中的常數10調節了改進擬合所需的總倍增因子的值。

此信息為每個項目分配因子提供了指導。

表2 檢查階段識別的要素以及項目1的分類水平

圖5 因子圖——簡單可預測

分配因子

分配階段的任務是按照檢查階段得來的指導原則，為過程添加結構，并產生更好的回歸分析。團隊現在進入到規范和執行階段，并通過討論和數學計算，進一步理解和完善了每個數據點。一些改進得到了認可，而另一些被否定，相關討論有助于進一步理清過程、加深理解。

理想圖提供了一個框架，用于定義和量化數據中的區別。每個理想的倍增因子被分解為如表2第5至第8列中的要素。這些要素提供了靈活性，并為每一行數據提供了確定適當范圍和粒度的單個總調整因子的方法。雖然主題專家在早期階段就熟悉了相關知識，但定義要素時還是包含了一些試驗和錯誤。

每個要素的分類水平、同等增量的水平都比較理想，如從0.25增至2的增量為0.25。不推薦不相等的增量，因為用它們來定位初始模型的特定數據點，效果雖然可能還行，但對于后續數據，它們卻具有相反效果，或被認為是強制產生解決方案或是操縱數據。

倍增水平——在0到2范圍內的所有要素，實質上都可以增加或減少數據點上的最終調整因子。調整回歸方程4中的理想倍增因子，可以給最終調整因子成為理想因子的機會。分類水平的例證請參考圖5。

就項目1來說，表1第1行中的分類水平產生了總調整因子，即1.75×1.50×1.25×1.25=4.1016。這個值接近理想的倍增因子：4.1612。與理想圖相比，這個初始數據點的位置相當低，這就促使大家進行深入討論，以解釋差異和不符。項目內和項目之間所定義的要素和分配的因子非常合理，在過程中也得到了有效體現。這些要素和因子還改進了回歸擬合，同時為每個要素的分類水平提供了定義。

回歸分析

回歸分析是一個強大的分析工具，也是迄今為止使用最廣泛的建模方法。該方法用于將過程輸出與一組輸入相關聯。

回歸分析階段的任務是當標準回歸分析沒有對過程進行充分建模時，產出一個簡單（易于理解和溝通）的線性模型。這個目標并不是通過多重回歸（即包含多個輸入的回歸）來完成的，而是通過簡單的線性回歸完成。為實現這一目標，檢查階段和分配階段完成了大量幕后工作。

當LEARN方法能夠正確實施時，運用回歸分析其實就成為一種形式。即使不熟悉回歸分析的決策者也會很容易理解表現為基本方程和散點圖的輸出形式。

團隊對表2中標為“繪制數據”的最后兩列進行了回歸分析。經過有效的討論，團隊改善了回歸擬合，以此證明了要素以其準確性和完整性改進了過程描述。圖5顯示了預測模型的巨大改進以及繪圖的簡單性。

要素不僅代表歷史數據，而且有助于更好地描述和理解未來的項目。通過運用本項目的過程知識來定制新項目，該模型就會對預期人工小時數產出更精準的估算。

雖然數據報告的讀者可能不熟悉“置信區間”術語，但通常我們還需要預測區間，也稱為用于預測的置信區間。95%的置信區間包含了樣本95%的平均輸出范圍。

由于副總裁對下一個項目規劃感興趣（即下一個單次觀測），所以進行區間預測是適當的。根據參數情況，可能會有多個預測區間方程。由于總體均值和總體方差未知，樣本量n=32支持假設的正態性，所以預測區間方程為：

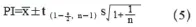
置信區間公式考慮了用于預測平均值的樣本變異性：

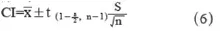
預測區間也考慮了預測單個響應相對于平均響應的不確定性，因此區間更寬。

請注意，決策者可能會設定雙重標準，又喜歡R2較高，但又不喜歡由此產生的緊密區間。

最后這個階段對于鞏固理解和展示交流至關重要，并不是畫蛇添足，這個階段是工作的可信性成敗的關鍵。大多數終端用戶都與過程相關，而不是與數學相關，因為要素反映過程，所以要素必須具備吸引終端用戶的常識。

這與要素如何以數學方式影響輸入是有區別的。分配的分類水平必須能夠滿足項目內部和項目之間進行比較的問題，識別適當的要素可能不那么容易或者不明顯。許多要素也可以改善模型的擬合，但卻并不適用于最后這一階段，因為它們在過程方面沒有任何意義和作為。

通過扎實的工程及數學計算，團隊確定了與過程相關及有影響力的方面。團隊將這些特點（即要素）挑選出來代表該過程，而其他較不重要的則放棄。最終的模型可放心應用。記錄每個項目的要素水平及選擇的理由，分享各自的理解，并增強工作的持久性和可信度。

在描繪了32個項目的特點之后，過程變得更好理解也更加穩定。隨著時間的推移，LEARN方法更加關注于維系易于理解的要素，并對新的項目進行回歸分析。而副總裁的期望僅僅是對未來計劃做出快速而準確的估計。

最終，異常數據點不再對因子模型的輸出造成威脅，而是可以促進指明原因的調查，例如團隊在發現某項目數據點較低后，將4個部門的工作進行了外包。

最后需要注意的是，初始數據集實際上是描述資源如何有效地為項目服務。分析中的主觀性——即初始模型中未能解釋的方差，是由于低效率（如不可預見的任務、學習曲線或倦怠）造成的。用于預測未來項目的實際人工小時數中也包含了這些低效行為。團隊認為，這些低效是過程中所固有的。

LEARN方法既無法鑒別也難以量化具體的低效來源，而是通過綜合人工小時數，以及投入、要素和因子的自然選擇，在最終的回歸階段對其進行解釋。

房間里的大象

過去，因為必要的數據不容易拿到而終止分析是可以接受甚至是可以預見的，但這種日子一去不復返了。“失敗再加上一個好借口”式的以營銷論英雄的日子也被取代了。如果問題容易的話，其他人早就解決了，而高級管理人員也不必再給專家打電話。雖然傳統評估看起來擁有廣泛現成的數據，但LEARN方法卻更深入探索了數據中的有效關系，同時還不影響分析的完整性。

持不同觀點的人會將本方法描述為一種強制形成解決方案，并使數據曲意迎合的方法。而事實上，LEARN方法并不強制形成解決方案，而是通過發現和應用增值信息將數據結構化為線性擬合。

是否可以通過這種方法來強制運用數學關系，使模型更好地實現擬合數據，并不反映過程實際，從而進行作弊呢？這取決于實際操作者。多種形式的描述型數學都有可能用來作弊。《如何運用統計數據作弊》一書自1954年出版以來，仍在銷售。

自然選擇過程中強加了制約和平衡，以確保基本因子富含信息，更重要的是使其適用于正在研究的過程。基本因子影響所有的數據點，而不僅僅是任何單個數據點，而且只有當實際數據和模型之間的差異總和變小時，模型才能得以改進。

LEARN方法通過模型擬合變好或變壞來對因子的相關性、有效性及其水平做出直接反饋。從根本上說，該方法并不總是有意識地去記錄，而是通過發現正在研究的過程特征來定位模型和過程，以最好地解釋兩者之間的關系。