仿鲹科機器魚雙體耦合波動推進動力學特性研究

薛文奎，謝 鷗

（1.常州機電職業技術學院 電氣工程學院，常州 213164；2.蘇州科技大學 機械工程學院，蘇州 215009）

仿鲹科機器魚雙體耦合波動推進動力學特性研究

薛文奎1，謝 鷗2

（1.常州機電職業技術學院 電氣工程學院，常州 213164；2.蘇州科技大學 機械工程學院，蘇州 215009）

采用數值模擬方法仿真分析了仿鲹科機器魚在不同波動頻率、波動幅度和初始相位差下的雙體耦合波動推進動力學特性，重點研究了同相和反向波動時的阻力和升力系數。實驗測試表明：雙體機器魚反相波動耦合推進速度比同相波動高，且游動更穩定。研究結果對仿生水下機器人的研制具有指導意義。

仿鲹科機器魚；波動推進；耦合；動力學特性

0 引言

魚類歷經數億年的自然進化，形成了獨具特色的游動能力，以適應復雜的海洋環境。受魚類優越的水下推進機制啟發，工程技術人員研發了各種仿生水下航行器[1,2]。此外，生物學家觀測發現，80%的魚類具有群游特性，尤其是小型魚類，幾乎是100%具有群游特性。眾所周知，在自然界，單條魚的力量很弱小，游動動作也很簡單，但作為一個群體，魚類在獵取食餌、逃避敵害和集群洄游等方面表現出驚人的力量。研究表明，魚類的集群游動蘊含著豐富的流體動力學原理。基于計算流體動力學方法（CFD），研究人員對串行排列的兩條仿生機器魚的游動情況進行了一系列數值模擬分析，結果發現，下游的魚能從上游魚產生的尾渦中吸收能量來提高推進效率[3～5]。然而，對于魚類并行游動的研究卻很少見報道，本文將以仿鲹科機器魚為研究對象，采用數值模擬和實驗研究的方法揭示并行排列的仿鲹科機器魚雙體耦合波動推進的動力學特性。

1 問題描述

按照產生周期性游動的生物推進器類型、部位和原理不同，魚類游動推進模式可分為兩大類：身體-尾鰭模式（Body and Caudal Fin, BCF）和中央鰭/對鰭模式（Median and/or Paired Fin, MPF）[6]。鲹科魚類是典型的BCF游動模式，其通過身體的后半部分在橫向方向往復地作扭曲擺動，以橫波的方式由前向后傳播以獲得推進力。如圖1所示，并行游動的兩條鲹科魚類，其尾鰭在波動過程中將通過流體互相耦合從而影響其推進性能。根據波動姿態的不同，本文重點研究同相和反相波動時的流體動力學特性。

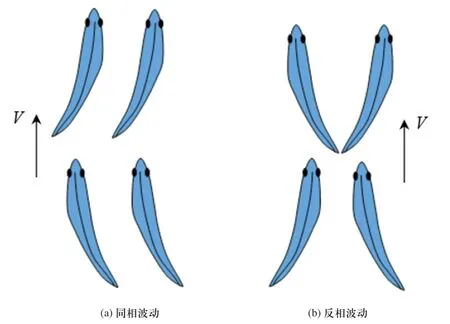
圖1 鲹科魚類并行游動耦合推進示意圖

2 動力學數值模擬分析

2.1 仿真建模

如圖2所示，在Fluent軟件中建立仿鲹科機器魚雙體耦合波動推進的仿真模型，每個機器魚由頭部和尾鰭兩部分組成，采用三角形非結構自適應網格對計算區域進行劃分，計算域的左邊界為速度入口，初始速度設為v=0.5m/s。采用動網格技術對機器魚的運動過程進行網格更新，仿鲹科機器魚的尾鰭運動可采用Lighthill提出的魚體波動方程進行描述[7]：

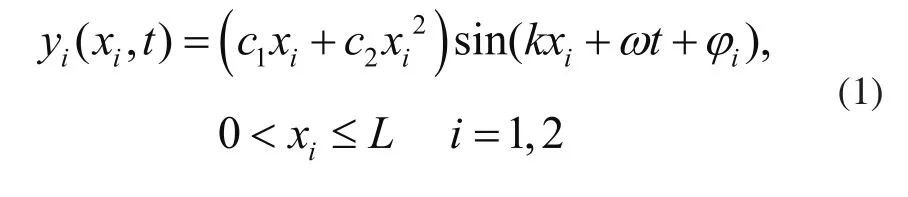
式中：yt(xi,t)表示第i條機器魚的橫向位移；c1，c2為波幅包絡線系數；xi為第i條機器魚的x軸坐標值；k為機器魚的體波波數；ω為機器魚的體波頻率；?i為第i條機器魚的初始相位差；L為機器魚的尾鰭長度。

本文設兩條機器魚的波動方程參數c1，c2，k和ω為相同的值，按下式控制尾鰭的初始相位差，實現同相和反向波動。

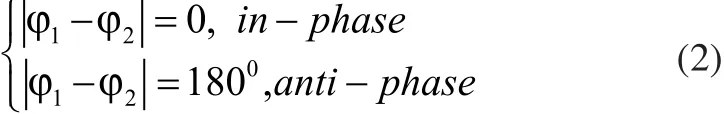
定義仿生推進器沿x軸負方向游動，游動過程的阻力系數Cd和升力系數Cl計算如下：

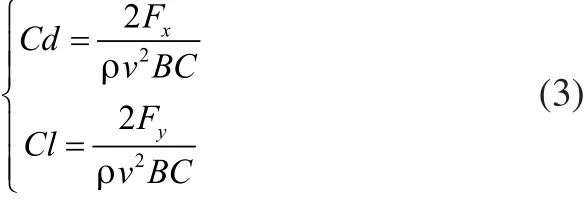
式中：Fx為x軸方向的流體阻力（也即推進力）；Fy為y軸方向的側向力；ρ為流體密度；B為尾鰭末端的擺幅；B為尾鰭特征弦長；v為來流速度。

Cd表明了機器魚產生的推進力大小，Cl決定了機器魚產生的無用功大小。本文采用Cd和Cl兩個參數分析仿鲹科機器魚雙體耦合波動推進的動力學特性。

2.2 仿真結果分析

圖2 鯵科機器魚雙體耦合推進仿真模型

如圖3所示為仿鲹科機器魚雙體耦合波動推進在一個運動周期內的壓力云圖。由圖3(a)可知，反相波動時，在兩個機器魚尾鰭張開階段T/4，會在尾鰭中部產生一個低壓區，同時在各尾鰭的根部會形成一個高壓中心，隨著尾鰭張開角度變大，高壓中心向尾鰭末端移動最后從尾鰭脫落。在尾鰭收合階段會在尾鰭中部形成高壓中心，隨著尾鰭的波動，高壓中心最后也從尾鰭末端脫落。由圖3(b)可知，同相波動時，在兩個機器魚尾鰭上擺過程T/4，上方機器魚尾鰭的上方會形成一個高壓中心，而在下方會形成一個低壓中心，隨著波動運動的進行，高壓和低壓中心同時向尾鰭末端移動，最后從尾鰭脫落。尾鰭下擺過程與上擺過程一致，只是高壓和低壓中心會在下方機器魚尾鰭上形成。

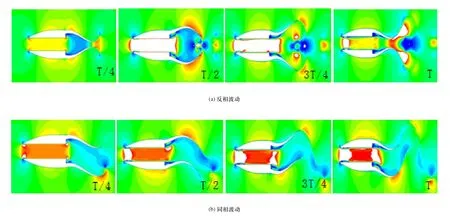
圖3 壓力云圖

如圖4所示為阻力系數和升力系數的時變曲線，由圖4(a)可知，同相波動的阻力系數曲線呈類正弦變化，且曲線的頻率是波動頻率的兩倍。反相波動的阻力曲線在一個波動周期內會出現一個尖峰脈沖，對應于兩個機器魚尾鰭收合到一起的時刻。由圖4(b)可知，同相波動的升力曲線也呈類正弦變化，曲線的頻率與波動頻率一致。反相波動的升力曲線則以0為中心呈無規則的波動，且在兩個機器魚尾鰭收合到一起的時刻出現大幅度的抖動。綜合對比可知，同相波動能產生平穩的持續推進力，而反相波動能提供瞬時的大推進力。在波動周期的大部分時間里，反相波動產生的升力要小于同相波動，其主要原因是反相波動時兩個機器魚各自尾鰭產生的升力大小基本一致而方向相反，故互相抵消。

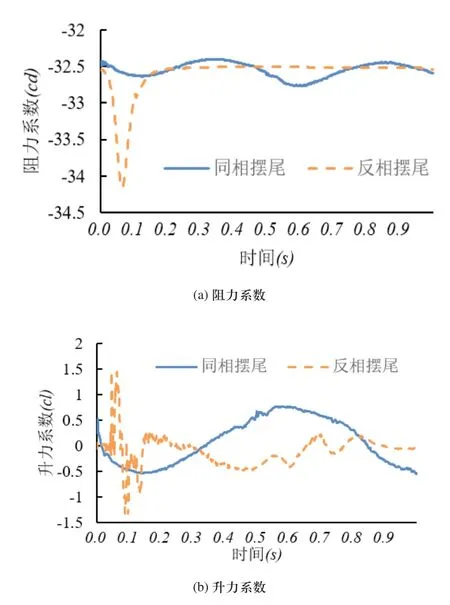
圖4 兩種波動模式下的時變阻力和升力系數曲線（主要參數：擺角30°，頻率1Hz，尾鰭間距200mm）

如圖5所示為尾鰭擺幅對阻力和升力系數的影響關系曲線。由圖5(a)可知，同相波動時，平均阻力系數的絕對值隨擺角增大呈線性緩慢增大趨勢。反相波動時，平均阻力系數曲線存在一個轉折擺角為20°。當擺角小于20°時，平均阻力系數的絕對值隨擺角增大而緩慢增大；當擺角大于20°時，平均阻力系數的絕對值隨擺角快速增大，其主要原因是：當擺角增大到一定值時，兩個機器魚尾鰭的耦合效應快速增大，從而產生了大的推進力。由圖5(b)可知，同相和反相波動的平均升力系數曲線都以0為中心呈無規則的波動，且同相波動的平均升力系數曲線的波動幅值明顯比反相波動大，表明同相波動將消耗更多的無用功，效率低。

如圖6所示為尾鰭波動頻率對平均阻力和升力系數的影響關系曲線。由圖6(a)可知，同相和反相波動的平均阻力系數的絕對值都隨頻率增大而增大，且反相波動的增長速度大于同相波動。由圖6(b)可知，同相波動和反相波動的平均升力系數的絕對值隨頻率的變化也呈無規則的波動。

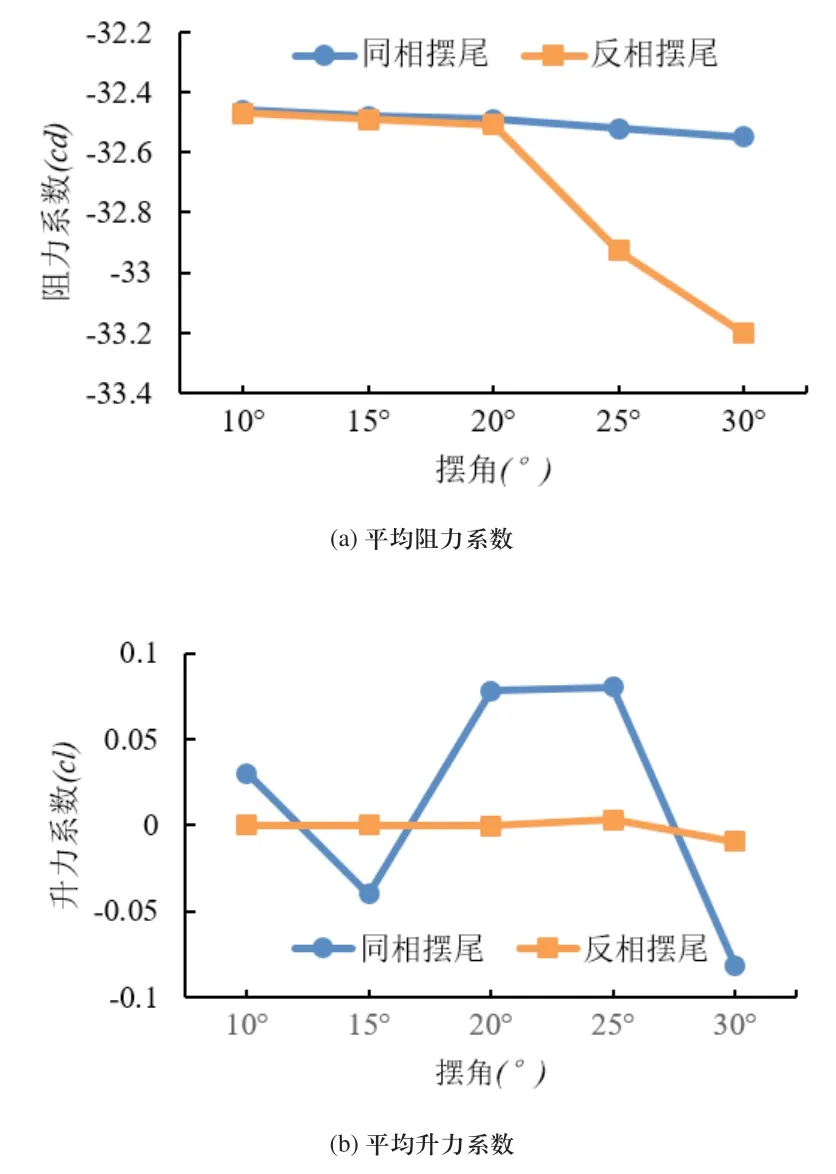
圖5 平均阻力和升力系數隨擺角幅度的變化關系曲線（主要參數：擺頻1Hz，尾鰭間距200mm）

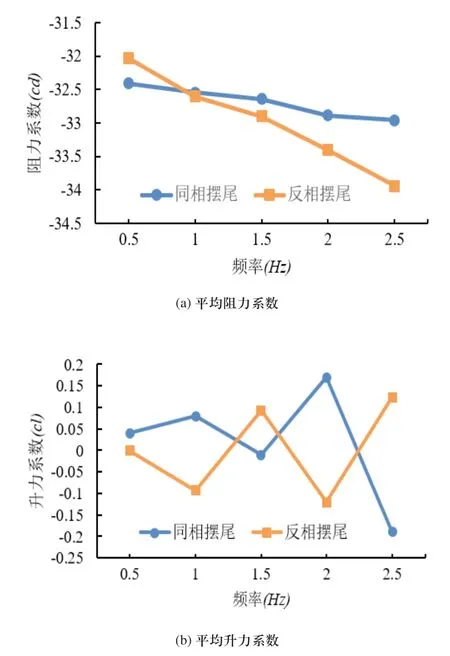
圖6 平均阻力和升力系數隨波動頻率的變化關系曲線（主要參數：擺幅30°，尾鰭間距200mm）

如圖7所示為兩個機器魚尾鰭的擺動相位差對平均阻力和升力系數的影響關系曲線。由圖7(a)可知，相位差以30°的增量從0°向180°變化時，平均阻力系數的絕對值呈遞增趨勢，且增長速率開始時較小，當相位差大于120°時增長速度變大。由圖7(b)可知，平均升力系數的絕對值在相位差為60°到90°之間時較小，而在其他情況下較大。

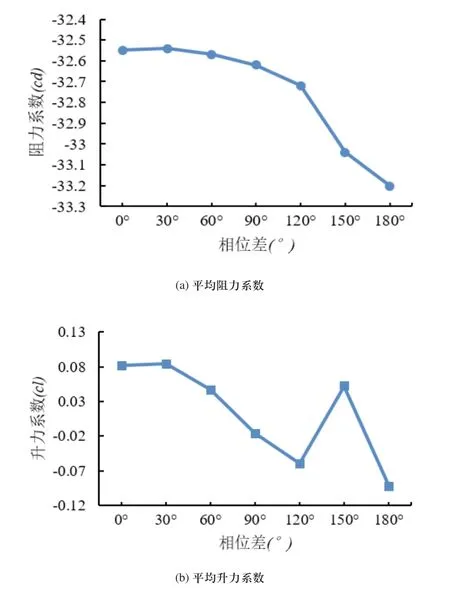
圖7 平均阻力和升力系數隨擺動相位差的變化關系曲線（主要參數：擺幅30°，擺頻1Hz，尾鰭間距200mm）

如圖8所示為兩個機器魚在不同間距下的同相和反相波動阻力系數曲線。由圖8(a)可知，反相波動時，減小尾鰭間距，阻力系數曲線將產生一個大的尖峰脈沖，尤其是間距為150mm時效果很明顯，表明兩個尾鰭之間產生了強烈的流場耦合效應。相比于反相波動，由圖8(b)可知，同相波動時，尾鰭間距對阻力系數的影響甚小。

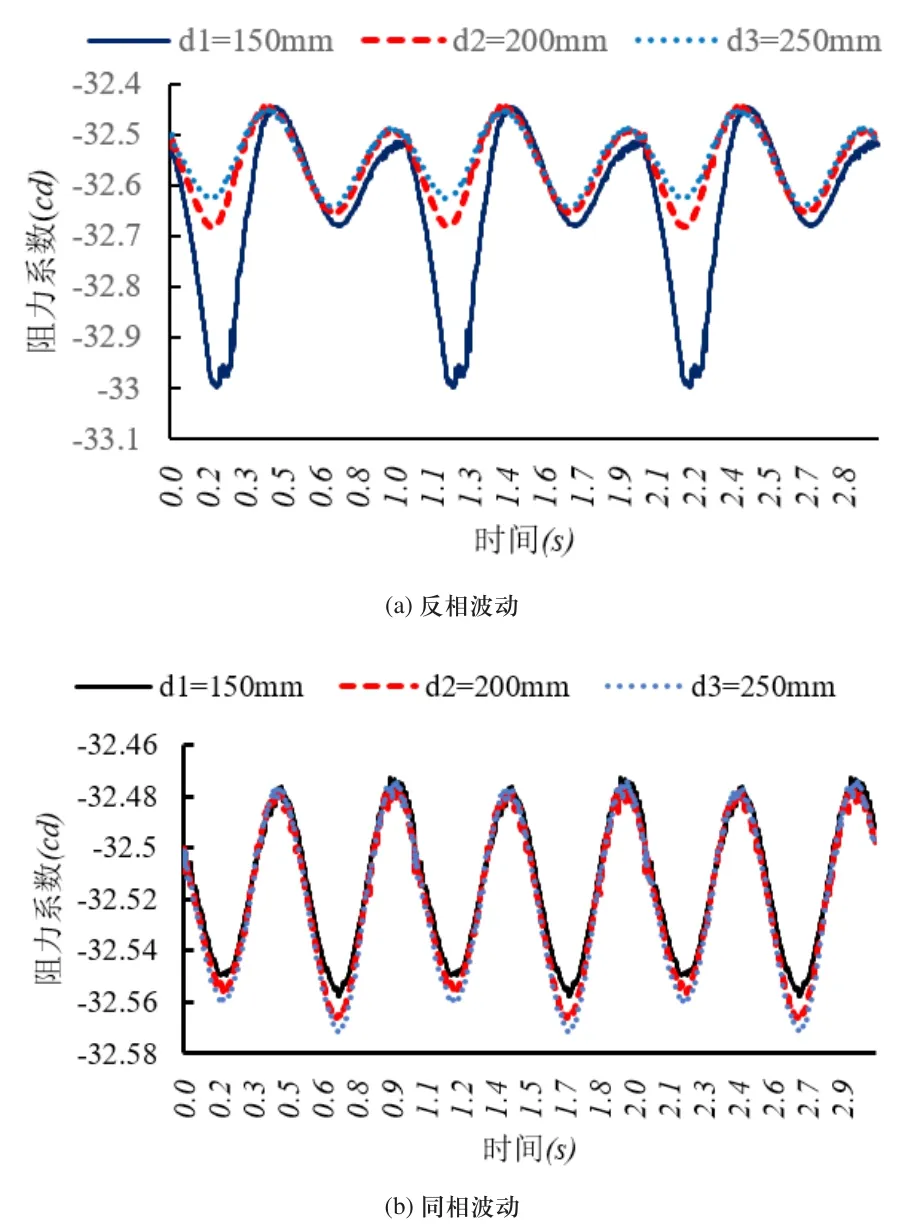
圖8 尾鰭間距對反相和同相波動阻力系數的影響（主要參數：擺角20°，擺頻1Hz）

圖9 仿鲹科機器魚雙體耦合推進視頻截圖

3 實驗研究

3.1 實驗過程

為了驗證仿鲹科機器魚雙體耦合波動推進的效果，本文采用自主設計的兩條獨立的三關節仿鲹科機器魚通過連桿支架組裝為雙體耦合推進裝置。如圖9所示，控制機器魚尾鰭的初始相位差可實現同相和反相波動推進。采用高速攝影機對機器魚游動過程進行錄像，記錄機器魚游動的距離和時間。將機器魚游動距離除以游動時間便可獲得游動速度，每組實驗重復三次取平均值。

3.2 實驗結果分析

如圖10所示為波動參數對仿鲹科機器魚雙體耦合波動推進速度的影響關系曲線。由圖10(a)可知，兩種波動方式下，推進速度都隨波動頻率增大而增大。相同波動頻率下，反相波動的速度明顯大于同相波動的速度。由圖10(b)可知，同相波動時，推進速度隨擺幅增大而緩慢增大。反相波動時，推進速度先隨擺幅增大而增大，當擺幅大于11cm時，推進速度呈下降趨勢。由圖9(c)可知，相位差從0°變化到180°時，推進速度呈上升趨勢。

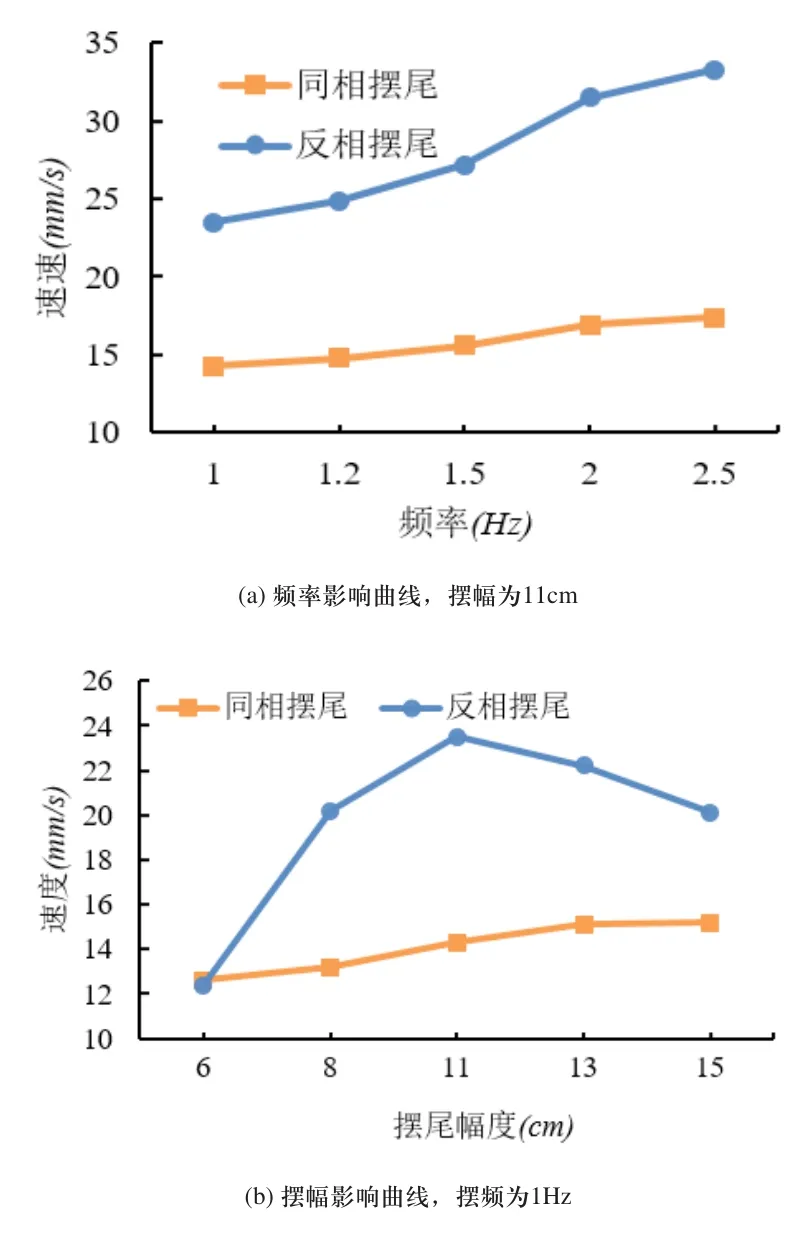
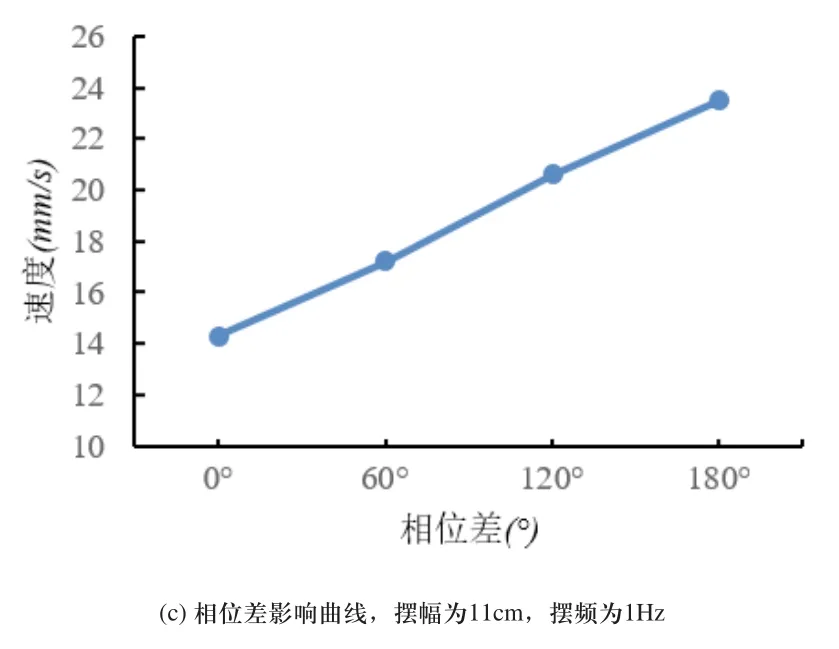
圖10 波動參數對仿鲹科機器魚雙體耦合推進速度的影響關系曲線

4 結論

針對鲹科魚類群游現象，采用CFD方法數值模擬了不同運動參數下仿鲹科機器魚雙體耦合波動推進的動力學特性，并利用自主研發的實驗裝置對仿鲹科機器魚雙體耦合波動推進的速度進行了測試。結果表明，并行游動的仿鲹科機器魚，尾鰭之間存在顯著流體耦合效應，改變尾鰭的運動參數可對耦合推進力和推進速度進行調節。

[1] 王安憶,劉貴杰,王新寶,等.身體/尾鰭推進模式仿生機器魚研究的進展與分析[J].機械工程學報,2016,52(17):137-146.

[2] 王揚威,于凱,閆勇程.BCF推進模式仿生機器魚的研究現狀與發展趨勢[J].微特電機,2016,44(1):75-80.

[3] Gopalkrishnan R, Triantafyllou M, TriaI1tafyllou G, et a1. Active vorticity control in a shear flow using a flapping foil[J].J Fluid Mech,1994,274(1):1-21.

[4] Deng J, Shao X M, Yu Z S. Hydrodynamic studies on two traveling wavy foils in tandem arrangement[J].Phys Fluids,2007, 19:104-113.

[5] 王亮,毛科峰,陳希,等.魚游尾跡中射流分布特征的數值模擬研究[J].中國科學,2013,43(9):1097-1104.

[6] C. M. Breder.The Locomotion of Fishes[J]. Zoologica,1926, 4: 159-297.

[7] M. J. Lighthill, Note on the swimming of slender fi sh[J].Journal of Fluids Mechanics,1960,9: 305-317.

Study on dynamic characteristics of two carangiform robotic fish coupling undulation propulsion

XUE Wen-kui1, XIE Ou2

TP242

A

1009-0134(2017)04-0143-05

2017-02-15

國家自然科學基金（51305287）；江蘇省自然科學基金（BK20130264）；江蘇高校品牌專業建設工程資助項目（TAPP）（PPZY2015C238）

薛文奎（1979 -），男，河南駐馬店人，講師，碩士，研究方向為計算流體動力學分析和機器人技術。