基于BA無標度網絡的WSNs拓撲優化模型
路智靜, 黃 如, 孫俊峰, 張 磊(華東理工大學信息科學與工程學院,上海 200237)
基于BA無標度網絡的WSNs拓撲優化模型
路智靜, 黃 如, 孫俊峰, 張 磊
(華東理工大學信息科學與工程學院,上海 200237)
由于無線傳感器能量受限,最大化網絡生命周期成為優化網絡拓撲首要考慮的問題。基于BA無標度理論,提出了一種WSNs拓撲優化模型(WTOM)。在網絡中引入超級節點,結合粒子群算法合理地劃分整個網絡;在節點間建立多因素為導向的虛擬力場,利用虛擬力調整超級節點的部署位置,實現網絡能量的均衡消耗,通過對關鍵節點的保護,提高網絡的抗毀魯棒性。經理論分析和實驗證明,該網絡不僅繼承了BA無標度網絡的特征還具有小世界特性;同時該動態拓撲延長了網絡的生命周期,提高了網絡面向數據收集的節能性。
無線傳感網絡; BA無標度網絡; 拓撲優化; 超級節點
隨著微電子技術、通信技術和計算機技術的飛速發展,無線傳感網路(WSNs)在軍事和民用各個領域都得到廣泛應用[1],然而無線傳感器節點受到部署環境限制,其能量不能得到及時補充。合理、高效的拓撲優化能夠實現網絡能量的均衡消耗和延長網絡的生命周期。而復雜網絡理論為建立可靠、高效的無線網絡拓撲模型提供了一種新的研究思路和方法。Wang等[2]通過對度分布熵的優化來調整無標度網絡結構,提升無標度網絡抗隨意性攻擊能力進而優化網絡的生命周期,但該拓撲模型沒有考慮能量消耗不均衡問題。文獻[3]在構建網絡拓撲時通過控制網絡節點飽和度和剩余能量等因素,提高了WSNs的抗毀性,延長了網絡生命周期,但是在拓撲模型構建時沒有考慮節點負載量,負載量高的節點會因耗能過快造成過早死亡,縮短網絡生命周期。Tao等[4]統計自同構群的對稱網絡軌道,提出通過優化網絡拓撲對稱,使網絡更趨于同步,該方法更側重對網絡模型同步性的研究,且沒有用到復雜網絡理論。文獻[5]在 BA無標度網絡基礎上提出了新的 WSNs拓撲結構演化模型,該模型對節點的隨機故障及失效具有較高的魯棒性,但對網絡模型具體特征沒有作出分析。文獻[6]利用小世界模型的聚類特性和邊界數的概念對 WSNs 進行拓撲優化,并在此基礎上引入了閾值機制,使網絡優化之后具有較高的聚類系數、較明顯的簇群結構,但平均路徑長度變化不大。文獻[7]在復雜網絡理論的基礎上,提出了一種新的加權局域 WSNs 演化模型在沙漠治理維護中的應用研究,推導出其度分布、強度分布、邊權重分布均滿足冪率分布特征,但沒有考慮到網絡拓撲的動態變化。文獻[8-10]在復雜網絡模型演化的過程中考慮了節點剩余能量對網絡增長的影響,但對網絡模型的抗毀性沒有作出分析。Zhu等[11]基于局域網世界(Local world)模型,分別提出了兩種無標度網絡模型(EAEM模型和EBEM模型)。在EAEM模型中,新節點優先連接能量高的節點;而在EBEM模型中,除考慮剩余能量以外,新節點優先連接度較高的節點,但沒考慮網絡拓撲的變化。本文提出了一種基于BA無標度理論的WSNs拓撲優化模型,以最大化網絡生命周期為目標,在網絡初始演化的過程中構造節點適應度函數,考慮了網絡剩余能量和節點度的共同影響。在網絡拓撲動態優化的過程中,通過粒子群算法合理分區處理,利用節點度、節點剩余能量、節點密度多因素主導的虛擬力對超級節點的移動和部署進行優化,提高網絡能量均衡消耗能力,實現關鍵節點的目標性保護。實驗證明該網絡還具有BA無標度特征和小世界特性的雙重特點。
1 系統模型
1.1 概述
無線傳感器網絡中普通節點易受到環境的限制無法充電,某些節點由于能量的過度消耗而過早死亡,影響了網絡的性能和生命周期。在網絡中可以嘗試添加能量高、儲存容量大、數據通信能力強的超級節點來改善網絡的拓撲特性。圖1示出了WSNs拓撲優化模型(WTOM)示意圖,如圖所示,普通節點分布在超級節點的周圍,按照WTOM模型初始化生成算法形成類似于蜘蛛網狀的結構。模型中sink節點是路由信息的目的地,超級節點具有較大的通信半徑。由于普通節點通信半徑的限制,遠離sink節點的普通節點最優選擇通過超級節點將信息傳遞給sink節點。本模型中超級節點與普通節點按照一定比例加入網絡中,網絡中超級節點的個數將直接影響網絡的整體性能。超級節點因為其自身的優勢會更優先連接網絡新加入的節點,同時超級節點也會影響其鄰居節點與新加入節點的連接。超級節點類似于小世界效應,現實網絡中都有這種現象。以文獻檢索為例,新的手稿往往引用本領域的經典文獻,曾引用過本領域經典文獻的文章,更容易受到新手稿的引用。
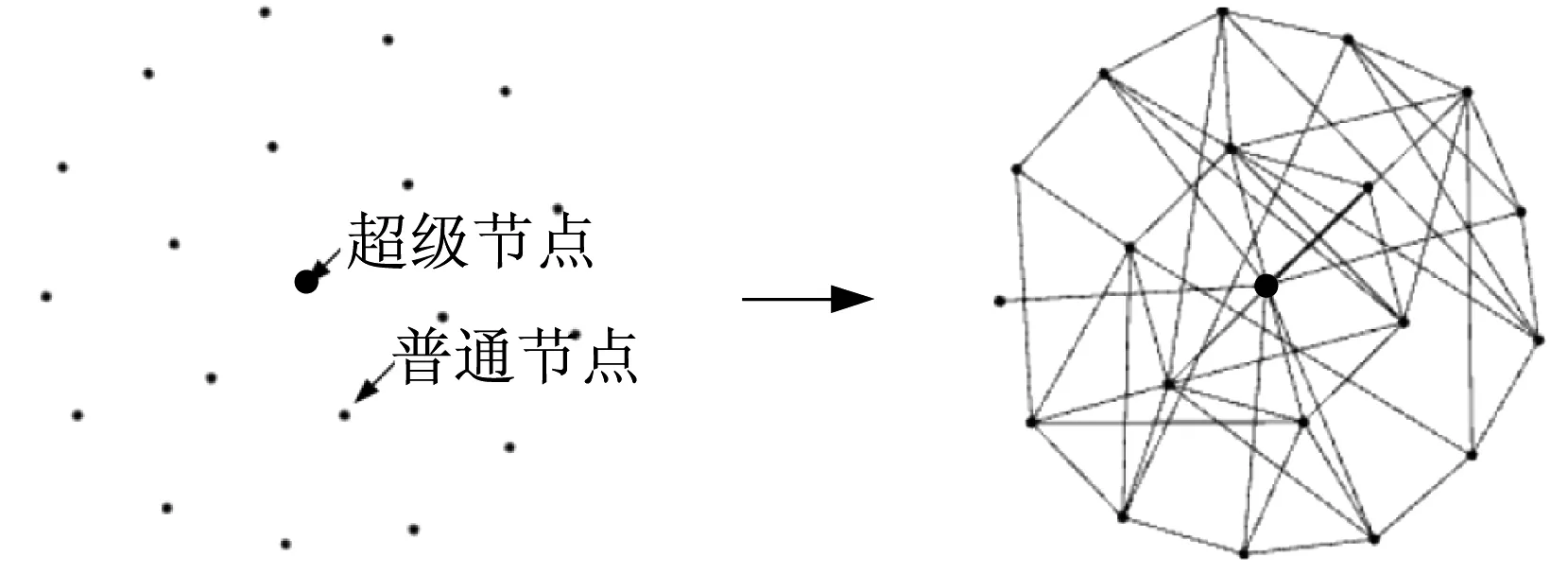
圖1 WTOM模型圖
1.2 模型前提假設
假設WSNs中隨機分散著N個節點,它們具備如下特點:
(1) 傳感器節點具有全局唯一的標識符ID。
(2) 普通傳感器節點部署到目標區域內不具有移動能力,隨機分布在正方形區域;超級節點具有移動能力;sink節點不具有移動能力,位于全局的中心。
(3) 在部署時,普通節點具有相同的能量;超級節點擁有幾倍于普通節點的等同能量,且它們的能量均不能得到補充;sink節點的能量足夠。
(4) 傳感器節點不能獲取地理位置信息,但能夠根據信號的強度計算發送節點到本節點的相對距離。
1.3 相關定義
(1) 度ki與度分布p(k)。節點i的度ki定義為與i相連的節點的數目。網絡中所有節點的度ki的平均值稱為網絡節點的平均度,記為
(1)
式中N為整個網絡節點數。節點度分布用分布函數p(k)表示,p(k)表示在網絡中隨機選定的節點的度恰好是k的概率。
(2) 平均路徑長度L。用L表示無線傳感網絡中所有節點發送數據到匯聚節點距離的平均跳數,Dj表示普通節點i到匯聚節點最短路徑的跳數。
(2)
(3) 聚類系數C。聚類系數定義為i的ki個鄰居間實際存在的連接數Ei除以節點i的鄰居間完全連接的總連接數,表示與i相連的點中任意兩點間相互連接的概率。
(3)
(4) 節點剩余能量與被選中連接關系f(E)。定義E表示剩余能量,f(E)表示節點剩余能量與被選中連接關系,節點的剩余能量越大,f(E)越大。當節點i為超級節點時,f(E)=nE,其中1 (5) WSNs生命周期。WSNs生命周期定義為網絡中能量耗盡或失效節點超過總節點數一半之前正常通信的周期數。 1.4 網絡拓撲動態優化機制 1.4.1 基于粒子群算法的網絡分區 利用粒子群算法將整個網絡中N個傳感器節點分成a個區,其中a表示超級節點的個數,則每個區中含有N/a個節點。首先確定一條網絡區域分割線,將網絡分割成兩個區域,兩個區域內節點數目相同。分割線形式如下: (4) 式中:x,y分別為為位于分割線上點的橫縱坐標;θ為分割線與x軸的夾角。 定義fitness函數如下: fitness=(d1-f1N)2+(d2-f2N)2 (5) 其中:di(i=1,2)為區域i中的節點數目;fi=ai/a(i=1,2),ai為期待超級節點的數目,即期待通過分割使得該區域保留多少個超級節點數。 (1) 對參數x,y,θ隨機賦值,由式(4)確定區域分割線,至此整個區域被分成2個不同的子區域,把兩個子區域節點的個數帶入式(5)。 (2) 確定多個不同的fitness值,與上次搜索得到的最小fitness值進行比較并取最小值,與其對應的粒子作為全局極值Pgd;同理,比較單個粒子得到的fitness值取最小的作為個體極值Pid,令α分別取值為x,y,θ,然后通過式(6)更新x,y,θ。 (6) 其中:Xxid,Xyid為粒子的位置;Xθid為分割線的傾角;vxid,vyid,vθid為粒子在x,y,θ3個維度上的搜索速度,由式(7)確定。 (7) 其中:c1,c2為學習因子;w為權重因子。 (3) 粒子得到合適的x,y,θ后,代入式(4)轉入步驟(1)的搜索,直到找到fitness值等于0或者近似0為止,此時,可以將整個區域分成節點數相等的兩個部分。 (4) 將區域首次分割之后,對兩個子區域繼續分割,直到分成a個規模相等的區域結束。 1.4.2 以虛擬力為導向的超級節點部署調整 當節點i為超級節點時,為各超級節點找到鄰近的子目標區域并調整其在子目標區域內的目標部署位置,在節點之間引入虛擬力,使超級節點在多因素影響的虛擬力作用下調整自身的部署位置。其中,各作用力取正數值時表示引力,取負數值時為斥力。 (1) 超級節點與同區域普通節點的作用力 (2) 子區域邊界對超級節點的作用力 其中:Dj表示超級節點對應目標子區域的邊界;|pi-Dj|是超級節點i距離重心Dj的距離;kbj是與兩子區域相互位置關系相關的一個參數;kd是一個反映節點密度的增益系數,反映相鄰子區域的節點密度與期望節點密度的關系;sn表示超級節點是否在目標區域內,若超級節點在目標區域sn取0,否則取1。 (3) 其他超級節點對超級節點i的作用力 其中:|pi-pj|為超級節點i,j之間的距離;d是一個固定值,為超級節點通信半徑的1.71倍;kij是一個增益系數。 本文模型采用基于改進BA模型網絡節點演化模型生成機制,并考慮到超級節點的影響,進而優化WSNs的網絡拓撲。 (1) 起始設定。假設網絡最初有m0個普通孤立節點,各普通節點儲能量相同。 (2) 增長性。每個時間間隔加入一個新的節點v,新加入的節點v為超級節點的概率為p,為普通節點的概率為(1-p),其中0≤p≤0.1,每次加入的節點v新增的度為m(m (3) 確定局域世界。距節點v最短時間加入的M(M≥m)個節點作為節點v的局域世界,其中M是隨時間增長的量,這M個節點均在節點v的通信范圍之內。 (4) 擇優連接。 若新增加的節點v與局域世界M已存在的節點i進行連接時,其連接概率為 (8) 其中:βi服從(0~1)分布表示超級節點的影響,如果網絡中新增節點與網絡中存在的超級節點或者超級節點的鄰居節點相連,則βi=1,否則βi=0。 (5) 重復步驟(2)~(4),達到要求的網絡規模N為止。 (6) 按照1.3節中網絡拓撲優化機制實現網絡的動態更新。 算法流程如圖2所示。 WTOM模型初始化完畢,在網絡動態優化的過程中,只有少量超級節點發生微小移動,因此并不影響網絡的整體拓撲。無標度網絡模型的動態特性可以用連續場理論進行分析論證[13]。考慮到連續性能更詳細地刻畫所提出模型的性質并預測其度分度,因此,運用連續場理論的方法進行數學論證。模型中任何一個節點的度隨時間變化的演化關系,可用連續場近似的方法求得。 當M≥m時,用ki表示節點i的度,并假設ki連續,則在每一個時間步中,節點i的度ki按照式(9)的比率增加。 圖2 WTOM模型初始化算法流程圖 (9) 式(9)的初始條件為:節點i在ti時刻進入系統,其度數ki(t)=m,且t>0,解微分方程可得 (10) t→+∞時,網絡的平均節點度為 (11) 由于時間t服從均勻分布,所以 (12) 由此可得,t→+∞時,節點的度分布趨于 (13) (14) 因為輸入超級節點的概率0≤p<0.1,故2 4.1 實驗參數設置 運用Matlab仿真工具和Gephi網絡構建工具,分析關鍵參數對WTOM模型的影響,并將WTOM模型與原始的BA模型在模型特點、平均路徑長度、聚類系數、能耗和生命周期方面進行對比。表1列出了實驗參數表,采用文獻[14]的通信模型模擬網絡能量的消耗,其中超級節點最大傳輸半徑為普通節點最大傳輸半徑的2倍,節點發射功率可調。 表1 仿真實驗參數設置 4.2 WTOM模型和BA模型比較 仿真實驗共分為兩組,第1組為按照WTOM模型擇優概率形成的模型,第2組為按照BA模型生成算法形成的模型,其中p=0.05。圖3(a)和圖3(b)為兩組模型圖。表2列出了兩組模型相同編號節點對應度的變化。圖3(a)中的編號節點為WTOM模型中的超級節點,圖3(b)中的編號節點為BA模型與圖3(a)中超級節點對應的相同編號節點。 由圖3(a)和圖3(b)及表2可知,WTOM模型中超級節點比BA模型中對應相同編號的節點連接的邊多,即度大。這是因為在WTOM模型中超級節點具有較高的能量,這樣有利于網絡能量的均衡消耗。 表2 WTOM模型和BA模型相同編號節點對應度的變化 圖3 WTOM模型(a)及BA模型(b) (N=100,p=0.05) 4.3 WTOM模型和BA模型度分布比較以及重要參數對WTOM模型度的影響 本文研究了WTOM模型和BA模型度分布的特征以及各關鍵參數對WTOM模型度分布的影響。圖4為p=0.05時WTOM模型和BA模型的實際度分布以及理想的度分布圖。p=0時,網絡中無超級節點,此時WTOM模型和BA模型完全相同。圖5為n取不同值時WTOM模型的度分布圖。 從圖4可知,WTOM模型和BA模型都具有度大的節點分布概率小、度小的節點分布概率大的特點。WTOM模型中,度在一段范圍內出現平坦的狀況,但從網絡整體度分布看,網絡具有無標度性;由于網絡中超級節點的存在,其度分布的冪指數變大,度較高的節點數目降低,這有利于降低網絡中某些節點因度過大消耗較多的能量,導致過早死亡。從圖5可知,適當地增加超級節點的能量也可以降低節點因過度消耗能量導致的失效,從而達到均衡網絡能量消耗,增加網絡穩定性的效果。 圖4 WTOM模型和BA模型度分布 圖5 超級節點能量對WTOM模型度分布的影響 4.4 WTOM模型和BA模型平均路徑比較以及重要參數對WTOM模型平均路徑的影響 圖6示出了WTOM模型和BA模型平均路徑分布圖。圖6表明添加超級節點可以有效地降低網絡的平均路徑,降低信息在網絡傳遞過程中的跳數;增加超級節點的能量對平均路徑幾乎沒有影響。圖7示出了超級節點個數對WTOM模型平均路徑的影響。圖7表明適當增加超級節點個數可以降低網絡的平均路徑,但達到一定數目時,網絡的平均路徑幾乎不再發生變化。 4.5 WTOM模型和BA模型聚類系數比較以及重要參數對WTOM模型聚類系數的影響 圖8示出了WTOM模型和BA模型的聚類特性。圖8表明WTOM模型具有較大的聚類特性,大的聚類系數使得局部網絡節點間連接具有更高的穩健性,增加超級節點的能量,聚類系數有所增加。圖9示出了超級節點個數對 WTOM模型聚類系數的影響。圖9表明增加超級節點個數,WTOW模型的聚類系數沒有規律地變化。 圖6 WTOM模型和BA模型平均路徑 圖7 超級節點個數對WTOM模型平均路徑影響 圖8 WTOM模型和BA模型的聚類系數 4.6 WTOM模型和BA模型抗毀魯棒性比較 為比較WTOM模型(p=0.1)和BA模型的抗毀魯棒性,表3中統計了WTOM模型(p=0.1)和BA模型最大連通分支上的節點數隨周期數r的變化結果。 圖9 超級節點個數對 WTOM模型聚類系數的影響 由表3可以看出,在通信過程中,WTOM模型比BA模型具有較好的抗毀魯棒性。這是因為WSNs節點的失效很大程度上是由能量耗盡引起的,而WTOM模型在拓撲構建的過程中考慮了剩余能量和度的影響,拓撲優化過程中考慮了對關鍵節點的保護,有利于維持網絡的連通性,從而提高了網絡的抗毀魯棒性。 4.7 WTOM模型和BA模型生命周期比較以及能量消耗分析 實驗采用SEP路由算法,實驗參數見表1。圖10(a)示出了存活節點數與周期數的關系;圖10(b)示出了能量消耗率與周期數的關系,均在N=100,p=0.1,n=2條件下進行實驗。 圖10(a)表明BA模型在進行300多個周期時節點開始死亡,而WTOM模型中節點到400多個周期時節點才開始死亡;超過310個周期后WTOM模型比BA模型存活的節點數多;除此之外WTOM模型比BA模型延長了整個網絡的生命周期。圖10(b)顯示BA模型節點能量消耗率高于WTOM模型的能量消耗率,WTOM模型有利于提高能量的利用效率,從而提高網絡的生命周期。 表3 最大連通分支上的節點數隨周期數的變化 圖10 WTOM模型和BA模型中存活節點數和能量消耗率的比較 本文基于BA無標度網絡理論,提出了一種拓撲優化模型。通過引入超級節點并結合粒子群算法將網絡合理地劃分區域;在節點間建立虛擬力場,利用虛擬力調整超級節點目的性的移動,實現網絡中關鍵節點的保護,均衡網絡節點的能量消耗。實驗結果表明與原始的BA模型相比該模型更具有小世界特性、延長網絡生命周期的特點。 [1]YICK J,MUKHERJEE B,GHOSAL D.Wireless sensor network survey[J].Computer Networks,2008,52(12):2292-2330. [2]WANG Bing,TANG Huanwen,GUO Chonghui,etal.Entropy optimization of scale-free networks robustness to random failures [J] .Physica A,2006,363(2):591-596. [3]ZHENNG Gengzhong,LIU Qiumei.Scale-free topology evolution for wireless sensor networks [J].Computers & Electrical Engineering,2013,39(6):1779-1788. [4]TAO Shaohua,YAN Jingfeng.Synchronization enhance on scale-free network[C]// 2011 3rd International Workshop on Intelligent Systems and Applications (ISA).USA:IEEE,2011:1-4. [5]ZHENG G,LIU S,QI X.Scale——Free topology evolution for wireless sensor networks with reconstruction mechanism[J] . Computers & Electrical Engineering,2012,38(3):643 -651. [6]李曉誠.基于小世界模型的無線傳感器網絡由算法的研究 [D].南京:南京郵電大學,2012. [7]姚洪興,周飛.基于復雜網絡的無線傳感器網絡在沙漠治理維護中的研究[J] .計算機應用研究,2014,31(10):3033-3036. [8]GUIDONI D L,MINI R A,LOUREIRO A A.Applying the small world concepts in the design of heterogeneous wireless sensor networks[J].IEEE Communications Letters,2012,16(7):953-955. [9]WANG D,LIU E,ZHANG Z,etal.A flow-weighted scale-free topology for wireless sensor networks[J].IEEE Communications Letters,2015,19 (2):235-238. [10]JIAN Y,LIU E,ZHANGN Z,etal.Percolation and scale-free connectivity for wireless sensor networks[J] .IEEE Communications Letters,2015,19(4):625-628. [11]ZHU H,LUO H,PENG H,etal.Complex networks-based energy-efficient evolution model for woreless sensor networks[J].Chaos Solitons & Fractals,2009,41(4):1828-1835. [12]劉軍,于耕,張慧鵬.基于節點控制的空間信息網絡拓撲重構算法[J].電子學報,2011,39(8):1837-1844. [13]CHEN Hongbin,TSE Chi K,FENG Jiuchao.Impact of topology on performance and energy efficiency in wireless sensor networks for source extraction[J].IEEE Transactions on Parallel and Distributed Systems,2009,20(6):886-897. [14]REN J,ZHANG Y,ZHANG K,etal.Lifetime and energy hole evolution analysis in data-gathering wireless sensor networks[J].IEEE Transactions on Industrial Informatics,2015,12(2):788-800. WSNs Topology Optimization Model Based on BA Scale-Free Network LU Zhi-jing, HUANG Ru, SUN Jun-feng, ZHANG Lei (School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237,China) Due to the limited energy of wireless sensor nodes, the maximization of the network lifetime has become one of the most important problemsin the optimization of the network topology.This paper presents a wireless sensor networks topology optimization model (WTOM) based on BA scale free network. Some super nodes are introduced into the network that is divided reasonably by using particle swarm algorithm. The virtual force field driven by multiple factors is established between nodes and the deployment position of super nodes is adjusted by the virtual force. Thus, the nodes' energy consumption is balanced and the robustness of invulnerability is improved by protecting key nodes. Both the theoretical analysis and experimental results demonstrate that the obtained network model not only keep the characteristics of BA scale free network, but also has the characteristics of small world. Moreover, the proposed model can extend the network life cycle and raise the network energy saving in data collection. WSNs; BA scale free network; topological optimization; super nodes 1006-3080(2017)02-0234-07 10.14135/j.cnki.1006-3080.2017.02.013 2016-06-20 國家自然科學基金(61501187,61365005);教育部基本科研業務基金(WH1315009);國際級大學生創新實踐基金(201410251044,201310251052) 路智靜(1989-),女,河南濮陽人,碩士生,主要從事物聯網研究。E-mail:nicylzj@163.com 黃 如,E-mail:huangrabbit@163.com TP391 A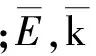
2 WTOM模型的生成機制
3 WTOM演化模型的數學分析
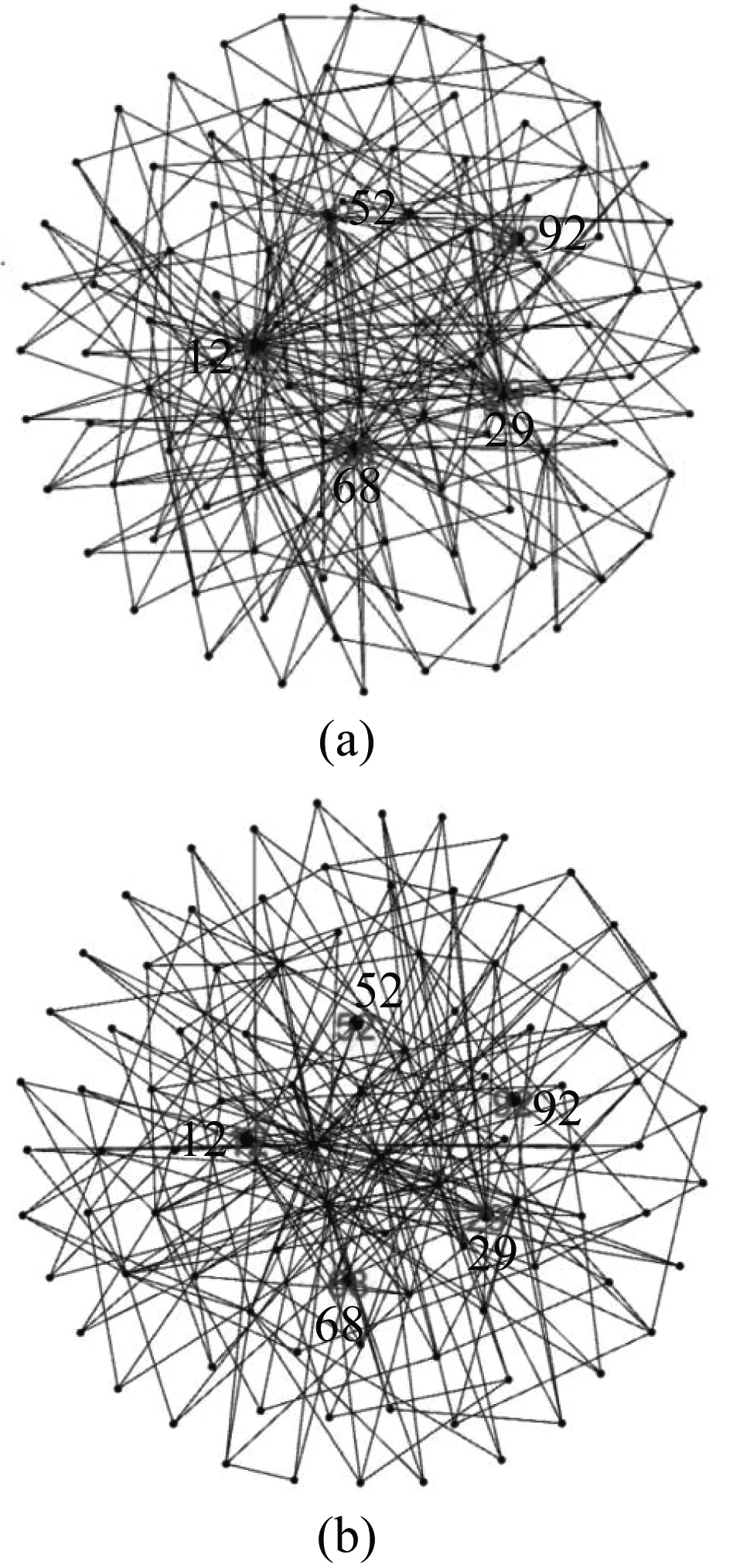
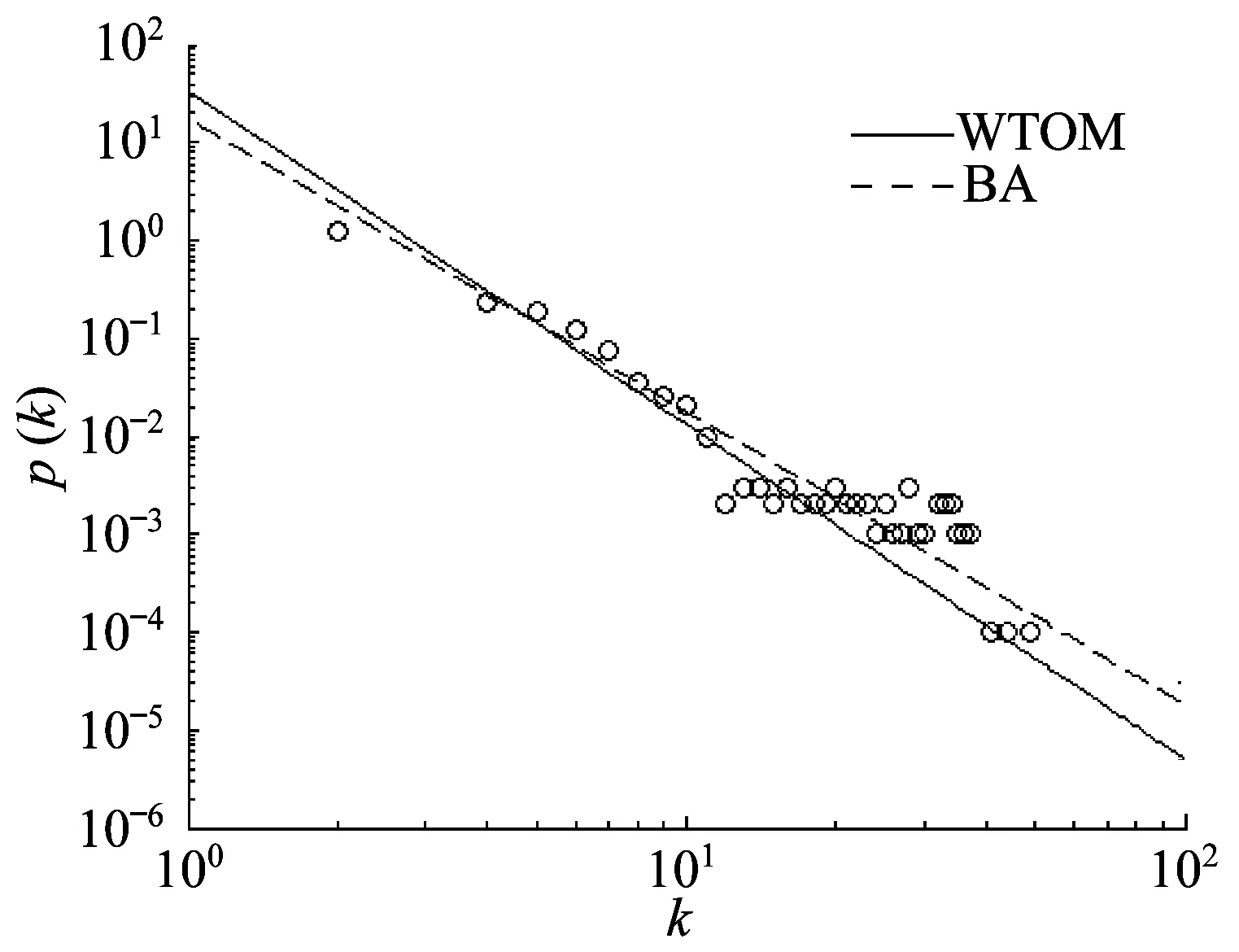
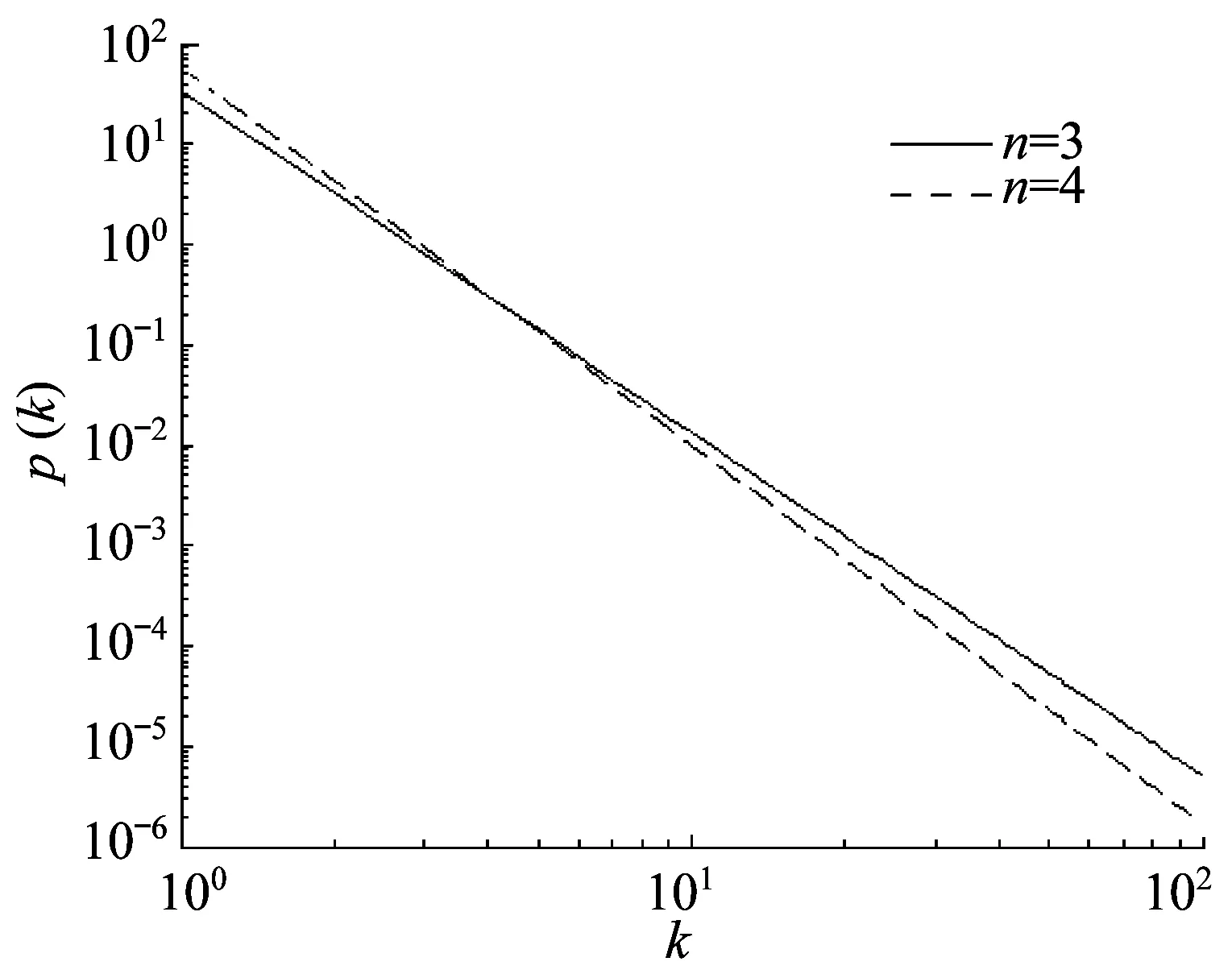
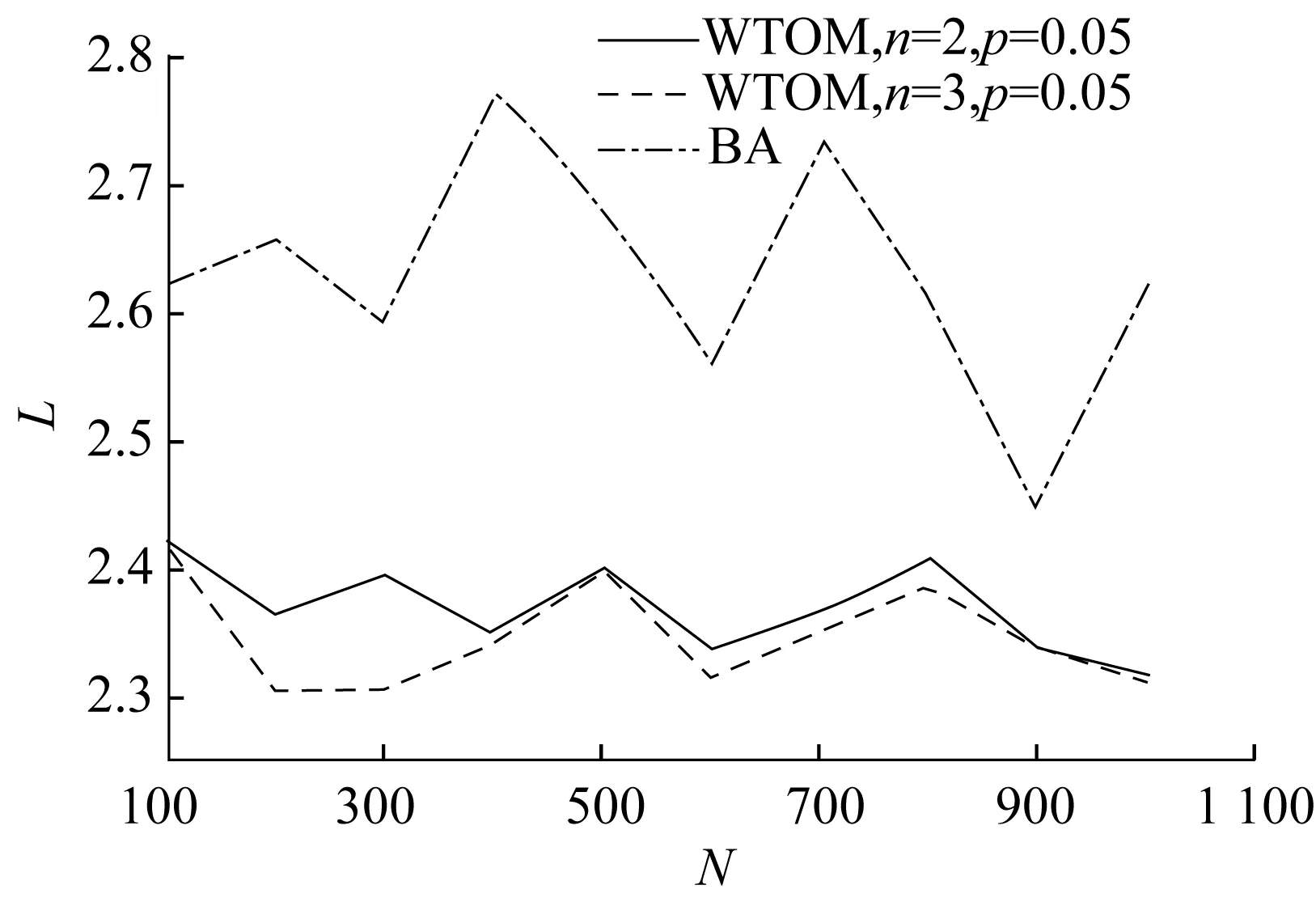
4 實驗仿真與結果分析

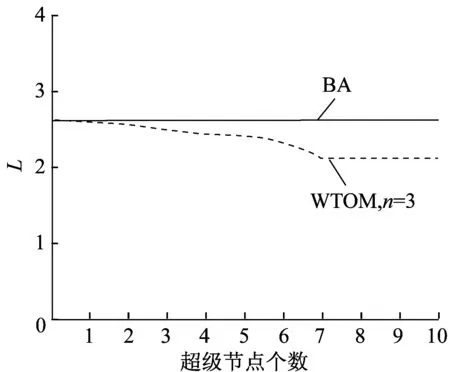
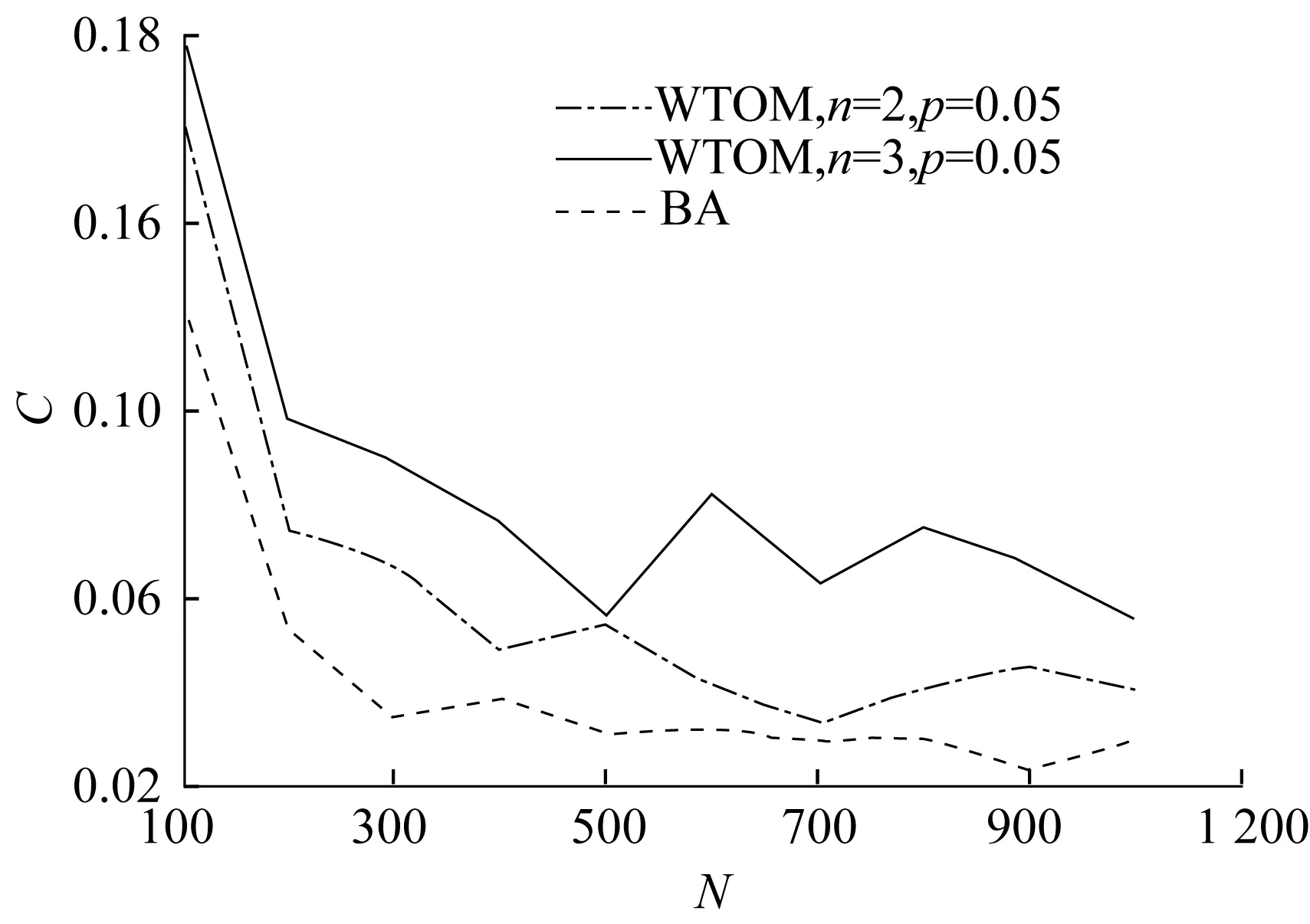
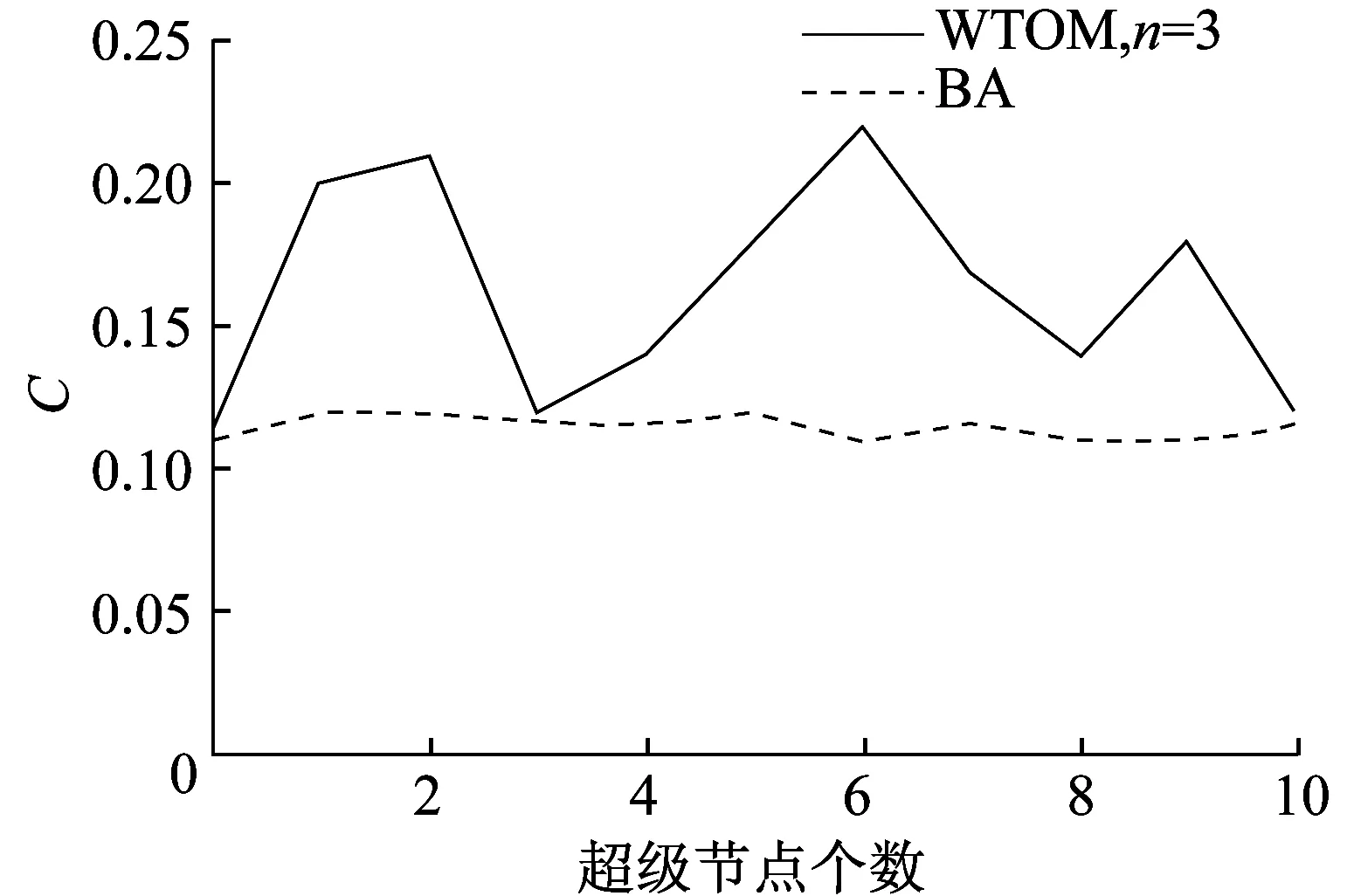

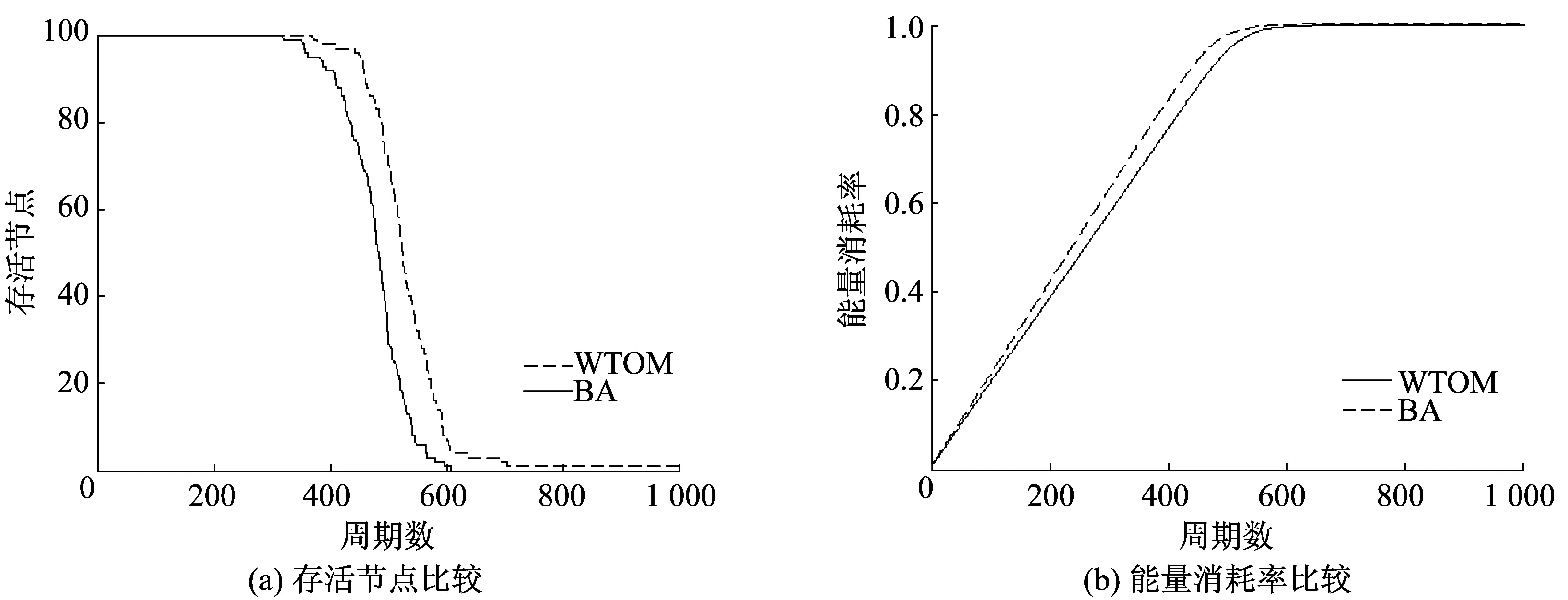
5 結束語

