沉降徐變的耦合受力性能分析

樊天望

同濟大學橋梁工程系

沉降徐變的耦合受力性能分析

樊天望

同濟大學橋梁工程系

在橋梁設計時，沉降一般認為是瞬時發生的，而對于粘性土來說，達到最終沉降的時間很長，因此研究沉降的時變特性是有重要意義的。本文以一座兩跨連續梁為例，進行考慮沉降時變特性和不考慮沉降時變特性的結構內力的理論上的推導，對沉降和收縮徐變耦合作用下的結構受力性能進行研究分析，并提出對基礎不均勻沉降作用的折減系數。

沉降；徐變；耦合；理論推導；受力性能；影響因素

0 前言

橋梁結構由于上部結構、橋梁墩柱以及承臺等的存在，對土會產生附加壓力，造成一定數值的沉降，這在橋梁設計中體現為基礎變位作用。在橋梁設計中，一般認為基礎變位是瞬時發生的。對于砂性土而言，可認為這基本符合實際情況，但對于黏性土來說，達到最終沉降的時間很長，有時候能達到數十年，在這種情況之下，在橋梁設計時，能否簡單地認為支座沉降是瞬時發生，而不考慮其長期時變效應，有待研究。此外，在沉降過程中，對于混凝土橋梁而言材料的收縮徐變也在發生，若考慮在沉降發生時收縮徐變同時發生，沉降對于橋梁結構的內力影響如何，更是有待分析。若考慮沉降時變效應下的收縮徐變作用，會影響結構的最不利受力，這將對結構的設計優化、材料節省及結構的準確分析等，產生積極有益的影響。因此本文以一座跨度為 和 的兩跨連續梁為例，進行考慮沉降時變特性和不考慮沉降時變特性的結構內力的理論上的推導，對沉降和收縮徐變耦合作用下的結構受力性能進行研究分析，并提出對基礎不均勻沉降作用的折減系數。橋梁結構示意圖如圖1所示：

假定此橋為一次落架，且假定此橋成橋內力為0，主梁剛度為EI，沉降時變規律為：，且不考慮收縮產生的內力及變形。

以下計算基于以上的假定。

1 不考慮沉降時變時的結構內力

在不考慮沉降時變特性時，可認為沉降為瞬時發生，之后再在此初始內力的基礎上發生收縮徐變。因此可分為以下兩部分進行計算：

1.1 瞬時沉降產生的結構內力

計算結構在瞬時沉降作用下產生的結構內力。此為超靜定結構，取中間支座處的彎矩為未知量，基本結構如圖2：

由相對轉角為0可得力法方程為：

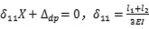
由幾何關系可知，中間支座沉降Δ0時，有：

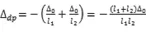
將以上兩式代入力法方程中，可得：

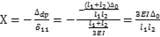
1.2 t1時刻的結構內力

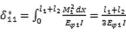
其中Eφ1為換算彈性模量Eφ1=γ (t1,τ0)E=

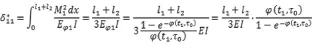
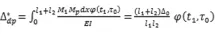
代入力法方程中，可得：

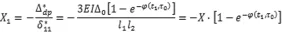
此即為徐變內力。可知徐變次內力和沉降產生的結構內力方向相反。同時徐變次內力和沉降產生的初始彈性內力成正相關。

根據以上計算，可知t1時刻中間支座處的內力為：

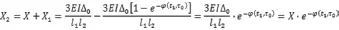
可知，t1時刻的內力為，為初始內力的，且內力一直變小，這與我們的理論知識相符合。

2 考慮沉降時變時的結構內力

考慮沉降時變特性時，認為沉降時變規律和徐變規律一致，假定最終沉降為Δ0，則t時刻值其沉降值為：

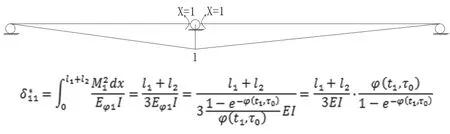
同上，取中間支座處的彎矩值為基本未知量，如圖3所示：

圖1

圖2

圖3

根據換算彈性模量法以及力法的基本概念，可建立相應的力法方程：

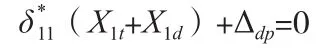
其中，X1d為在t時刻中間支座處由于支座沉降產生的彈性內力，而X1t為t時刻的徐變次內力。而t時刻內力之和為=X1t+X1d，因此力法方程可寫為：

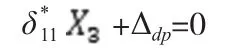
Δdp為支座沉降產生的相對轉角，由幾何關系可知：

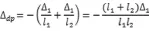
將以上兩式代入力法方程中，可得：

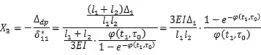
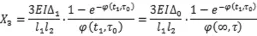
由上式可知，t1時刻的中間支座處的內力可知隨著時間的推移結構內力越來越大。

3 內力比較

由以上兩種情況下的結構內力理論計算可知，不考慮沉降時變特性時t1時刻中間支座處的內力為，考慮沉降時變特性時t1時刻中間支座處的內力為，兩者之間的比值為：

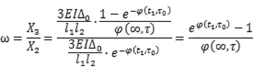
由比值可以看出，開始一段時間的同一時刻考慮沉降時變特性的內力要比不考慮沉降時變特性的內力要小，一段時間之后，同一時刻時考慮沉降時變特性的內力要比不考慮沉降時變特性的內力大。這是符合理論情況的，因為最初不考慮沉降時變特性時認為沉降終極值是瞬時發生的，相比較考慮時變特性的沉降產生的內力自然是要大的，因此最初一段時間考慮沉降時變特性的內力要比不考慮沉降時變特性的內力要小，過了一定時間之后，隨著考慮時變特性的沉降大部分完成，沉降產生的彈性內力相差不大；同時初內力較大時徐變內力也同樣較大，因此不考慮時變特性時徐變次內力要比同一時刻考慮沉降時變特性的內力大，對沉降產生的彈性內力減小的更多，因此后期同一時刻考慮沉降時變特性的內力要比不考慮沉降時變特性的內力大。

同時可以看出，兩者之間的比值只取決于徐變系數的變化規律以及徐變系數終極值，與終極沉降值的大小、跨徑的大小以及兩跨連續梁的相對大小無關，影響兩者比值的因素只取決于徐變系數，也即取決于影響徐變系數的因素。

當然，跨徑以及終極沉降值不影響兩種情況下的比值，卻都會對結構的內力值產生一定的影響。跨徑減小時，線剛度變大，因此同樣沉降值情況下內力變大；而沉降值越大內力也越大，從以上兩個結構內力的公式也可以印證這一結論的正確性。