電網歷史數據缺失及補錄研究

謝翹楚, 姚毅

(1.四川理工學院自動化與信息工程學院, 四川自貢643000;2.人工智能四川省重點實驗室, 四川自貢643000)

電網歷史數據缺失及補錄研究

謝翹楚1,2, 姚毅1,2

(1.四川理工學院自動化與信息工程學院, 四川自貢643000;2.人工智能四川省重點實驗室, 四川自貢643000)

電網歷史數據是智能電網信息化發展的基礎，確保歷史數據的完整非常必要。在分析電網數據采集與傳輸過程中產生數據缺失原因的基礎上，對缺失數據進行了類型劃分，并給出了發現和判定數據缺失的方法。根據數據缺失類型，采用缺失數據清潔法和缺失數據補錄法處理規律缺失數據和不規律缺失數據，使用SPSS驗證上述方法，結果表明補錄準確度高達90%；運用隨機森林算法處理不完全規律缺失數據，以均方根誤差和填補準確度為評判指標，實驗結果證明了該方法的準確性和有效性。用這些方法處理電網的數據缺失問題，能有效地提高電網歷史數據的質量，使現有的數據得到最大程度的利用。

電網歷史數據；數據缺失；數據補錄；隨機森林

引言

近年來，隨著全球智能電網的飛速發展，國家電網公司為我國的智能電網建設提出了新的要求，發展高速、高效的智能電網系統變得勢在必行[1]。

智能電網技術就是實現信息化、自動化、互動化，構建以特高壓為骨干網架、各級電網協調發展的統一。電網的歷史數據就是智能電網信息化建設的數據基礎。然而在實際中，各個變電站的數據在提取和傳輸時，會產生海量的雜亂無章的數據，其數量級別是呈指數級增長的，這些數據在傳輸和使用的過程中，有相當一部分數據因為人為因素或客觀因素發生了缺失的現象，對智能電網的信息化建設帶來了很大的不便。為了提高電網數據的質量，保障數據的完整性，為智能電網的發展掃清障礙，解決電網數據缺失是很有必要的。

本文闡述了智能電網變電站監控系統所產生的數據傳輸過程，并針對在傳輸過程中所產生的數據缺失問題，提出了處理數據缺失的方法。

1數據缺失的產生原因及類型

電網的監控平臺可以管理一部分區域內的所有變電站，并將其產生的海量數據進行數據挖掘分析，獲取其中有用的數據，尋找到一定的規律，對智能電網建設起到積極作用[2]。

整個電網系統中，數據的傳輸大致可分為單向流傳輸與雙向傳輸，本文主要研究單向流傳輸的數據缺失。傳輸過程為：個體變電站→數據集控站→縣級調度→市級調度→省級調度。

數據在傳輸過程中，會產生很多的缺失，產生缺失的原因大致可分為兩類，主觀原因和客觀原因。人為因素所導致的數據采集或傳輸造成的數據缺失可稱為主觀原因，如錄入數據失誤、工作失職或有意偽造數據所造成的數據缺失。設備故障、路線中斷等客觀原因所造成的數據缺失可稱為客觀原因，如數據存儲失敗、變電站機械故障、數據傳輸路線截斷等。

盡管變電站的歷史數據屬性眾多且繁雜，但是根據數據產生缺失的原因，大致可以把數據缺失情況歸為三類：無規律缺失、規律缺失、不完全規律缺失[3]。

無規律缺失是指該數據是完全隨機的，其數據類型不能由已知的數據類型來判斷。規律缺失是指該數據是有規律可循的，其數據類型可以由已知的數據來補充或推斷。不完全規律缺失是指該數據中既有無規律缺失數據，也有規律缺失數據。

2數據缺失的發現

數據缺失問題在基于傳感器采集數據的發電廠普遍存在，嚴重阻礙了電力科學與工程數據分析及挖掘在變電站優化領域的發展。

變電站數據采集、存儲系統組成復雜，測點工作環境惡劣等多方原因能夠造成數據的缺失，主要分為: 傳感器故障、數據傳輸故障、數據存儲故障、人的主觀因素等。數據的不完整性給數據挖掘過程、數據分析和研究帶來了重重困難，這些不完整的數據會導致分析結果發生偏置，建立錯誤的數據挖掘模型，導致不準確的挖掘結果，甚至會誤導用戶的決策，導致經濟損失[4-7]。

依據數據類型的重要程度來劃分數據的級別，例如首先將變壓器(油中溶解氣體、局部放電等)，高壓斷路器(氣體成分)，高壓母線(溫度)設定為優先級較高的數據，其次對各級別的數據依照以往的正常數據量設定相應的閾值，如果數據量低于閾值，即可判斷數據發生了缺失，再次根據即時數值與閾值的差距，對數據的缺失情況進行評級[8]。在對數據進行檢測時，若發生數據缺失，系統會根據數據的優先級別和閾值來一一判斷數據在哪個部位發生了缺失。

不同類型的數據缺失情況，應該有相應的缺失發現機制。

(1)規律缺失數據的發現

若數據缺失是呈規律性或遵循函數而發生的，系統會將其判定為規律缺失數據。

(2)不規律缺失數據的發現

若數據缺失是呈無規律性或隨機發生的，系統會將其判定為不規律缺失數據。

(3)不完全規律缺失數據的發現

若數據缺失即存在規律數據缺失又存在不規律數據缺失，系統會將其判定為不完全規律缺失數據。

3數據缺失的處理

傳輸中產生數據缺失會對整個電網監控平臺的實際效果產生巨大的負面影響，因此，對這些缺失的數據進行處理變得勢在必行。根據現在大數據處理技術對于數據缺失的處理辦法，可以對電網產生的數據缺失使用缺失數據清理法和缺失數據補錄法。在數據量較大時，普通的人工補錄效率會十分低下，而一般的基于統計學原理的補錄方法(如采樣法、回歸預測法、EM算法等)會出現較大的偏差，這就需要設計更加適合的補錄決策。

3.1缺失數據清潔法

缺失數據清潔法主要分為刪除法和權重法。

刪除法是處理缺失數據最簡單的方法，就是將缺失的個體直接刪除。如果直接刪除掉一部分個體數據就可以達到預期數據的目標，這個方法是最有效的。

權重法即當缺失值的類型為規律缺失時，通過對整體的數據加權來降低整體數據的偏差。把數據缺損的個體分別記錄后，用線性回歸法求得缺損數據各個部分的權重，然后將整體的數據個體給予有差異的權重。假如個體數據類型中存在對權重估計起決定性因素的變量，那該方法可以降低數據的缺損程度。假如個體數據類型中的變量和權重并不相關，那它并不能降低數據缺損程度。所以針對多個數據類型缺失的情況，就需要對不同類型的缺失組合給予有差異的權重，這將會加大數據處理的工作量，使預期結果發生偏移[9]。

缺失數據清潔法可運用于電網監控系統中表現較為良好的設備所產生的數據，但當數據類型比較復雜或設備產生的問題較多時，此類方法將會加大決策人員工作量，導致不能精確分析問題產生的原因，降低電網數據分析效率等。

3.2缺失數據補錄法

大數據處理技術的背景下，當海量數據出現一定的缺失情況時，如果單純地使用數據清潔法，會造成許多有用數據的遺失，這會對之后的數據挖掘和分析產生巨大的負面影響。因此，對缺失數據進行預估和補錄的對策(數據補錄法)應運而生。

根據規律缺失數據和無規律缺失數據和不完全規律缺失數據，采用相應的方法解決。

3.2.1規律缺失數據補錄

針對規律缺失數據，運用系統已形成的規律數據，建立相應的線性回歸方程式和決策樹，對缺失的數據進行預估，形成相應的預測數據，使用相應的預測數據對缺失的數據進行替換，此方法的準確程度將會隨著數據庫中線性回歸方程式和決策樹的準確度的提升而提升[10]。

采用最小二乘法計算線性回歸方程：

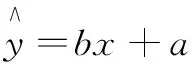
(1)

(2)

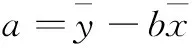
(3)

當式(1)中a、b取得最小值時，則稱式(1)為該數據的線性回歸方程，式(2)與式(3)為求解線性回歸方程的方式。

這里采用SPSS的數據缺失處理進行規律缺失數據的實證。數據庫為1978-2005年的電量使用率。首先使用SPSS的數據缺失值替換功能(圖1與圖2)；然后發現缺失值(圖3)；再對缺失值進行補錄(圖4)。

圖1SPSS選擇替換缺失值

圖2智能選擇替換方法

圖3發現缺失值

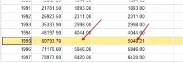
圖4對缺失值進行補錄

如圖4所示，根據以上的原理，系統對缺失的數據生成了一個新的補錄值5048，而1995年該變電站的實際電量使用量為5429，準確度超過90%，證明此方法在實際工作中有效，能有效提升電網歷史數據質量。

另外還可以采用就近補齊法和多重補錄法應對不同程度數據缺失情況的補錄。其中，就近補齊法是在之前未發生缺失的相近數據中找到與缺失值最為相似的一個值來補錄，但相對需要的人工時間較多，適用于對于相對重要的數據缺失的補錄；多重補錄法是通過記錄之前所有缺失的數據所形成的一個數據庫來匹配相應的缺失數據，根據缺失值的規律特征從數據庫里調出匹配度最高的數據來進行補錄。

3.2.2無規律缺失數據補錄

針對無規律缺失數據，目前采用平均值補錄最為有效，即將這些無規律的數據類型進行分類，取與該缺失數據屬性相近的數據平均值與該類數據進行替換[11]。

3.2.3不完全規律缺失數據補錄

在數據量特別大且數據類型多為不完全規律缺失數據時，如何對數據缺失的類型進行分類和處理，就要運用到大數據處理中的隨機森林原理。

如文獻[12]所述，隨機森林顧名思義，是用隨機的方式建立一個森林，森林里面由很多的決策樹組成，決策樹相互之間是沒有關聯的。在得到森林之后，當有一個新的輸入樣本進入的時候，就讓森林中的每一棵決策樹分別進行判斷，判斷這個樣本應該屬于哪一類，然后判斷哪一類被選擇最多，就預測這個樣本為哪一類。

通過總結之前發生數據缺失的數據特征，形成相應的決策樹，通過這些決策樹群對新的數據缺失樣本進行分類。

按這種算法得到的隨機森林中的每一棵都是很弱的，但是決策樹的數量多了就會對決策結果準確率產生較強的正面影響。總之，在隨機森林算法中，每一棵決策樹就是一個精通于某一個窄領域的“專家”，這樣在隨機森林中就有了很多個精通不同領域的“專家”，對一個新的問題(新的輸入數據)，可以用不同的角度去看待它，最終由各個“專家”，投票得到結果。這樣可以較為準確的對已知數據樣本的類型進行智能的分類[13]。

隨機森林中的每一棵分類樹為二叉樹，其生成遵循自頂向下的遞歸分裂原則，即從根節點開始依次對訓練集進行劃分；在二叉樹中，根節點包含全部訓練數據，按照節點純度最小原則，分裂為左節點和右節點，它們分別包含訓練數據的一個子集，按照同樣的規則節點繼續分裂，直到滿足分支停止規則而停止生長。若節點n上的分類數據全部來自于同一類別，則此節點的純度I(n)=0，純度度量方法是Gini準則，即假設P(Xj)是節點n上屬于Xj類樣本個數占訓練。

具體實現過程如下：

(1) 原始訓練集為N，應用bootstrap法有放回地隨機抽取k個新的自助樣本集，并由此構建k棵分類樹，每次未被抽到的樣本組成了k個袋外數據。

(2) 設有n個變量，則在每一棵樹的每個節點處隨機抽取m個變量，然后在m中選擇一個最具有分類能力的變量，變量分類的閾值由通過檢查每一個分類點確定。

(3) 每棵樹最大限度地生長,不做任何修剪。

(4) 將生成的多棵分類樹組成隨機森林，用隨機森林分類器對新的數據進行判別與分類，分類結果按樹分類器的投票多少而定[13]。

這里采取均方根誤差(RootMeanSquareError，RMSE)和填補準確度(Accuracy)評價算法的優越性。均方根誤差ERMSE是缺失值填補研究中應用最廣泛的評價標準:

(4)

式中：xr為真實值；xi為算法的填補值；n為缺失值的數目；ERMSE值越小說明算法填補質量越高[14]。

填補準確度A評價函數能夠計算出填補值中符合容忍度要求的值所占的比例：

(5)

式中：n為缺失值數量；nT為正確估計值數量。填補值在真實值的±10%以內都可被視為在容忍度范圍之內，即為正確估計值[15]。

將隨機森林算法與當前填補效果較好的SVR-OCSFCM算法[16](即支持向量回歸與遺傳算法優化的模糊聚類填補算法)進行比較，取某變電站的油紙絕緣中局部放電量、油中火花放電量及油中電弧為數據集，以油中電弧為填補量，對這兩種算法得到的均分根方差和填補準確度進行分析比較。根據分析得的結果如圖5與圖6所示。

圖5填補結果的均方根誤差

圖6填補結果的準確率

由圖5與圖6對均方根誤差與填補準確率分析可知，隨著缺失率的提升，隨機森林算法在均方根誤差和填補結果準確率上都要優于SVR-OCSFCM算法。

4結束語

將這些數據缺失處理方法應用于電網數據處理中，大大提升了數據的可用性，提高了電網各類數據的挖掘分析效率，將有效推動我國智能電網的建設與發展。

[1] 李佳瑋,郝悍勇,李寧輝.電網企業大數據技術應用研究[J].電力信息與通信技術,2014,12(12):20-25.

[2] 于存水.基于智能電網調度系統的調度監控平臺的設計與實現[D].長春:吉林大學,2013.

[3] 李麗.數據缺失及處理方法探析[J].湖南城市學院學報:自然科學版,2016,25(1):118-119.

[4] DRISCOLL M.Duke Energy's data modeling & analytics initiative[R].2014.

[5] 武森,馮小東,單志廣.基于不完備數據聚類的缺失數據填補方法[J].計算機學報,2012,35(8):1726-1738.

[6] 韋鋼,王飛,張永健,等.負荷預測中歷史數據缺損處理[J].電力科學與工程,2004,20(1):16-19.

[7] DONG L J,LIU X,ZHANG Q,et al.Design and implementation of metering abnormal and online diagnosis system of new generation intelligent substation[J].Applied Mechanics & Materials,2014,678:343-351.

[8] 侯廣松.變電站故障數據處理與分析系統研究與開發[D].濟南:山東大學,2014.

[9] 葉素靜,唐文清,張敏強,等.追蹤研究中缺失數據處理方法及應用現狀分析[J].心理科學進展,2014,22(12):1985-1994.

[10] 吳劉倉,張家茂,邱貽濤.缺失偏態數據下線性回歸模型的統計推斷[J].統計與信息論壇,2013,28(9):22-26.

[11] 趙志文,何靜花,楊慧超.Rayleigh分布總體參數的均值填補估計和檢驗[J].佳木斯大學學報:自然科學版,2016,34(2):285-288.

[12] AURET L,ALDRICH C.Change point detection in time series data with random forests[J].Control Engineering Practice,2010,18(8):990-1002.

[13] 曹正鳳.隨機森林算法優化研究[D].北京:首都經濟貿易大學,2014.

[14] 卜范玉,陳志奎,張清辰.基于聚類和自動編碼機的缺失數據填充算法[J].計算機工程與應用,2015,51(18):13-17.

[15] 李建強,趙凱,潘文凱,等.電站歷史數據缺失值填補策略研究[J].電力科學與工程,2017,33(1):43-48.

[16] 唐闊,胡國圣,車喜龍,等.基于遺傳算法優化支持向量回歸機的網格負載預測模型[J].吉林大學學報:理學版,2010,48(2):251-255.

Research on the Data Missing and Data Completion of Power Grid

XIEQiaochu1, 2,YAOYi1, 2

(1.School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China; 2.Artificial Intelligence Key Laboratory of Sichuan Province, Zigong 643000, China)

The completion of data is needed in the development of smart grid, so it is necessary to improve the data quality of smart grid. The transmitting procedure of the smart grid’s big data is introduced and the reasons of the data missing and the type of missing data in the process of data transmission are analyzed. According to the analysis of the missing data cleaning and the missing data collection, the problems of irregular missing data and missing data patterns are solved. Then SPSS is used to validate the methods. The results show that the accuracy rate is as high as 90%. The random forest algorithm is introduced to deal with the incomplete data. And the accuracy and effectiveness of the above methods are proved by the experiments. The methods to the data missing problems of smart grid above will effectively improve the quality of the smart grid data and get the most use of existing data.

smart grid; data missing; data completion; random forest

2016-12-12

四川理工學院研究生創新基金項目(20141210)

謝翹楚(1991-),男,四川自貢人,碩士生,主要從事大數據處理方面的研究,(E-mail)luckyxc1991@163.com

1673-1549(2017)02-0021-05

10.11863/j.suse.2017.02.05

TP274

A