一種高泛化能力的神經網絡氣動力降階模型

尹明朗, 寇家慶, 張偉偉,*

(1. 西北工業大學 翼型葉柵空氣動力學國家重點實驗室, 陜西 西安 710072; 2. 布朗大學 工程學院, 美國 普羅文登 02906)

?

一種高泛化能力的神經網絡氣動力降階模型

尹明朗1,2, 寇家慶1, 張偉偉1,*

(1. 西北工業大學 翼型葉柵空氣動力學國家重點實驗室, 陜西 西安 710072; 2. 布朗大學 工程學院, 美國 普羅文登 02906)

神經網絡模型的泛化能力是指模型對于新樣本的適應能力，而當前基于神經網絡的非線性氣動力模型往往泛化能力不足。針對這一局限，發展了一種基于計算流體力學的帶驗證信號氣動力降階模型，用于跨聲速氣動力預測。采用遞歸徑向基函數神經網絡，通過引入差分進化算法，對模型中隱含層神經元寬度進行優化，優化目標為驗證信號的均方根誤差最小。訓練信號采用結構大幅振蕩的位移和氣動力響應，用小擾動下微幅運動的信號作為驗證信號。算例表明建立的降階模型不僅具有比全階數值模擬更短的計算時長，并且由于采用了小幅運動的驗證信號，使模型在不同頻率和振幅下的泛化能力得到增強。

非定常氣動力；降階模型；神經網絡；泛化能力；驗證信號

0 引 言

20世紀90年代后期， 受NASA與美國空軍資助的一些氣動彈性專家，如Dowell[1]與Silva[2]等，提出了基于CFD數值模型構造流場降階模型(Reduced-Order Model, ROM)的理論，有效地降低了計算時間并保證了計算精度。ROM是一種在保證計算精度與降低計算時間的條件下，將流場全階模型通過降階的模型進行替代的方法。

目前流固耦合系統中非定常流場的ROM主要有兩類[3]：基于本征正交分解[4]的ROM與基于系統辨識方法的ROM(Volterra級數[5]、帶外輸入的自回歸[6]模型、遞歸結構的代理模型[7]、神經網絡模型[8])。此外還有一種非線性氣動力的諧波平衡方法[9](Harmonic Balance, HB)被用于氣動力求解。其中，因為系統辨識方法中的神經網絡模型具有主動學習、容錯性強和具有強大的預測非線性系統的能力等優勢，所以一批學者針對神經網絡建模進行了深入的研究。例如Lindhorst[10]通過使用徑向基函數(Radial Basis Function, RBF)神經網絡并結合POD與Markov鏈與對兩自由度的氣動彈性系統建模，但并不能預測大幅迎角升力系數以及力矩系數；Ghoreyshi[11]等基于RBF神經網絡，運用Euler與N-S方程的氣動力響應同時進行模型訓練，提高了預測精度，但只是針對低速情況；史志偉[12]等基于兩步回歸參數辨識法，建立了兩步線性回歸的狀態空間模型，并預測了某飛機三角翼在俯仰與偏航運動時的氣動參數。但該模型有其自身結構的局限性，不能準確地預測更為復雜的運動情況，且模型精度有待提高；Zhang[13]等與王博斌[14]等通過引入RBF神經網絡的輸出反饋，可以有效模擬非定常流場中的遲滯現象，構建的基于遞歸向基函數(Recursive Radial Basis Function, RRBF)神經網絡的氣動力模型，分別預測了升力系數、力矩系數以及極限環顫振響應。但從文獻[13]的分叉點預測結果可見，模型對不同振幅的泛化能力仍然不理想。綜上，神經網絡氣動力建模存在的問題總結起來可以歸結于兩點：計算精度不足與模型泛化能力不足。

前人也對提高神經網絡建模精度以及模型泛化能力做出了一系列研究。針對模型精度的提高，Du[15]等提出了在同一染色體中編碼結點、輸入和中心與寬度，用遺傳算法進行全局尋優，但尋優過程復雜，不容易實現；Kurkova[16]等提出通過核方法來提高RBF模型的泛化能力，但是高階Volterra核難于計算；寇家慶等[17]提出用ARX模型預測線性部分輸出、用神經網絡模型預測非線性部分輸出來增強模型來增強模型的泛化能力，但是寬度的選取通過試錯法，效率較低。對于RBF神經網絡模型預測氣動力最主要的影響因素之一就是神經元中心寬度，所以針對每個神經元找到其所對應的最優寬度是RBF神經網絡模型精度與泛化能力的關鍵。

為解決寬度的選擇問題，以保證更好的泛化能力，本文發展了一種使用差分進化算法優化與引入小幅高頻驗證信號計算非線性氣動力的RRBF模型，采用固定的神經元位置，針對每一個神經元的寬度用差分進化算法進行尋優，并且引入驗證信號作為優化目標，在避免過擬合的情況下增強模型泛化能力。

1 氣動力建模

本文發展了帶驗證信號的差分進化算法優化遞歸徑向基函數神經網絡(Differential Evolution-Recursive Radial Basis Function Neural Network, DE-RRBFNN)，此模型是一種基于CFD的神經網絡氣動力模型，屬于基于系統辨識的降階模型。

1.1 遞歸徑向基函數神經網絡

RRBF神經網絡是將靜態RBF神經網絡引入動態延遲而來，前者繼承了RBF神經網絡的結構。如圖1(a)，RBF神經網絡可實現映射X→Y,X∈Rq,Y∈Rl,l>1，(X是一個q維的輸入向量，Y是對目標輸出函數的逼近，為l維向量)。Y表達式為：

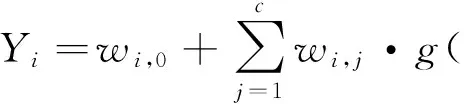
該神經網絡模型有c個隱含層神經元，wi,0為神經網絡偏移，wi,j為第i個輸出對第j個隱含層神經元的權重，g為高斯基函數。

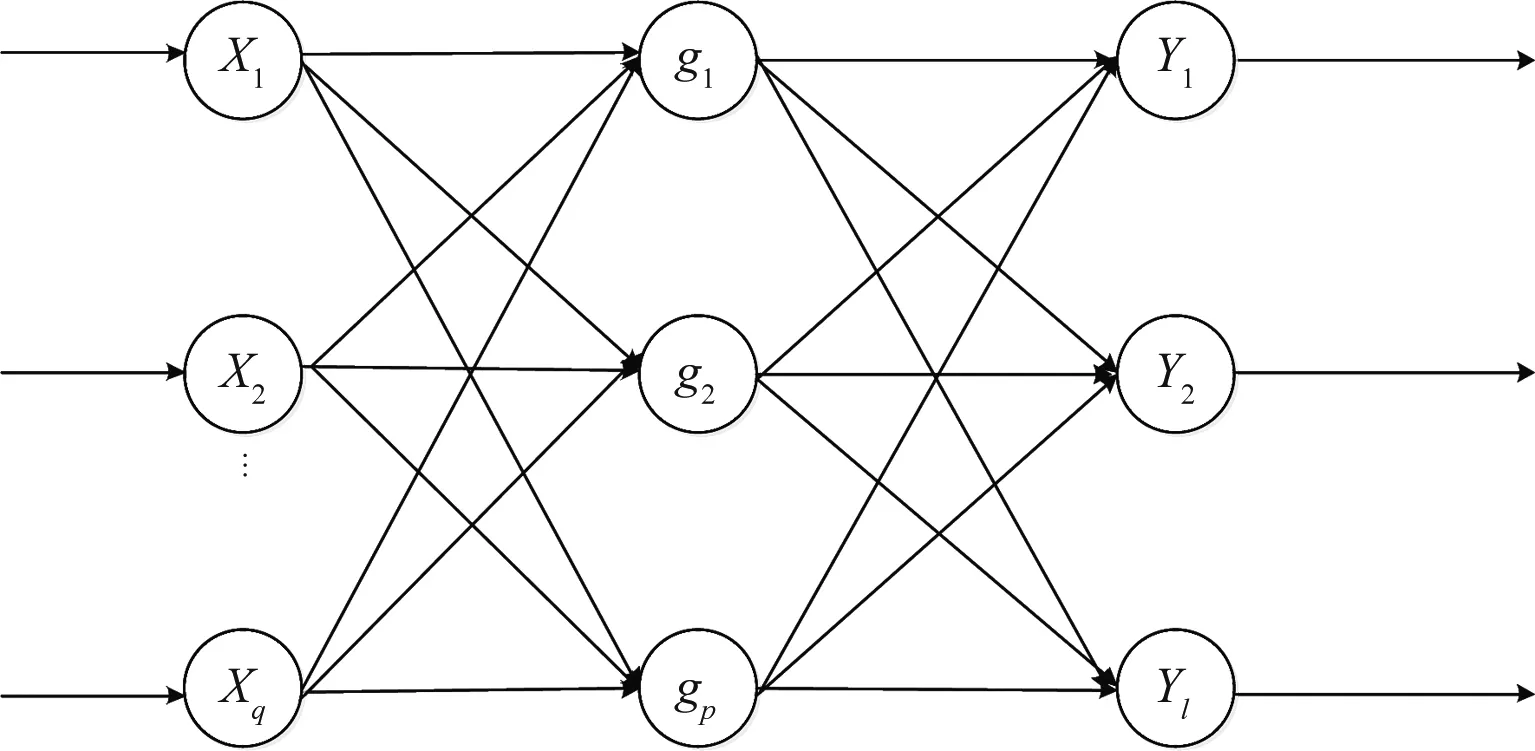
(a) RBF神經網絡結構

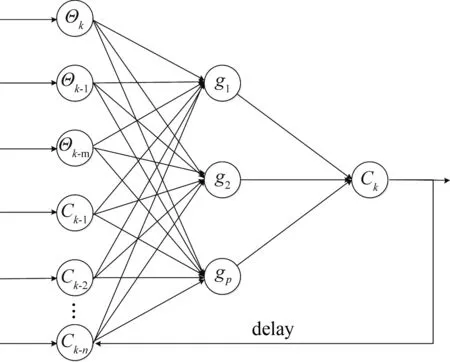
(b) 遞歸神經網絡結構

在計算遲滯效應很強的非定常氣動力時，RBF神經網絡由于不帶反饋，便出現了自身的局限性。RBF神經網絡從本質上來講是一個準定常模型，所以計算定常流場時的結果精度較高。但是對于計算非定常效應十分明顯的流場時，模型的結果將具有很大誤差。若提高模型的非定常流場計算能力，還需改變其固有屬性，即通過引入輸出反饋體現非定常效應。

此模型依托的RRBF神經網絡是一種三層遞歸式網絡，分別為輸入層、隱含層和輸出層。輸入層由神經元結點組成，如圖1(b)。作為外輸入的每一個神經元結點通過非線性函數映射，映射至隱含層的每一個神經元中，并構成隱含層。最后，隱含層通過線性映射(與各個神經元權重相乘)到輸出層并在輸出層中反饋部分信號至輸入層[13]。

RRBF模型是一種有效的改變RBF神經網絡模型準定常屬性的新模型。該模型在輸入端引入了部分輸出層的輸出，即升力系數和力矩系數。計算升力時，模型的輸入如下式：

計算力矩系數時，模型的輸入如下式：

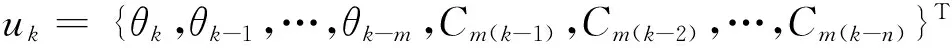
(4)

在計算k時刻結果時引入了k-1至k-n時刻的結果，也就是k時刻結果是基于k-1至k-n時刻結果得來的(n為延遲階數，也就是引入輸出層結果至輸入層的個數)。這樣就增強了所計算結果與之前結果的關聯性，也就是增強了預測非定常流動之間的遲滯效應的能力，所以RRBF模型更加適合計算非定常氣動力。

RRBF模型工作流程如下：如圖1(b)，通過CFD求解器計算機翼俯仰運動下的升力系數、力矩系數。隨后，將俯仰位移作為RRBF模型輸入，經過高斯基函數映射至隱含層，然后再經線性映射至輸出層，得出升力系數與力矩系數。之后再將升力系數與力矩系數帶回至輸入層，與下一時刻位移輸入一同組成該時刻的輸入。

1.2 寬度的影響

寬度是高斯基函數作用范圍的表征。由式(2)可以看出，寬度的不同可以使隱含層輸出有所不同。相同的輸入下，寬度越大，隱含層輸出越小。同時寬度的調整也關乎最后模型的準確性，不同中心寬度的模型具有不同的精度，最優的參數也能使模型獲得最優精度。寇家慶[18]等通過研究寬度對模型精度的影響，發現對RRBF神經網絡氣動力模型采用不同寬度可能跟大程度影響模型的泛化能力。以往的模型設定的是神經元之間同一寬度。但是實際上，由于非線性輸入的存在，使得神經元之間的距離不一致。這樣的不準確的寬度設置導致了很大的預測誤差。所以為了提升精度，該模型使用差分進化算法對隱含層神經元的寬度進行調整，以增強該模型的泛化能力。

1.3 差分進化算法

差分進化(Differential Evolution, DE)算法實際上是一種并行導向性搜索方法，可以通過NP個向量xi,G,i=1,2,…,NP搜索多代進行尋優[19]。該算法簡單易用、穩健性好、有強大的全局搜索能力、待定參數少、不易陷入局部最優、收斂速度快。上述優點使得差分進化算法十分適合搜索最優寬度矩陣。

差分進化算法的一次計算過程如圖2所示。此算法是一個迭代過程。先由計算機對每個神經元生成一個一定范圍內的隨機數,也就是1×P維的寬度矩陣。然后通過一定規則變異、交叉并產生新個體。再比較新個體與未變化之前的個體的適應度函數(該寬度下，模型預測的升力與CFD計算得到升力系數之差的2-范數)，選擇出優秀個體。之后再次變異，交叉種群中的個體生成新個體直至種群所有個體都經歷過以上運算，最后選擇出優勢個體，保存并重復以上步驟G次。此算法中的交叉、變異是模仿生物DNA在復制中的變異與交叉過程。變異是保證初始向量中的個體能夠變異，而交叉則是保證一段序列能夠變異。變異與交叉實為尋找全局最優解的保證。

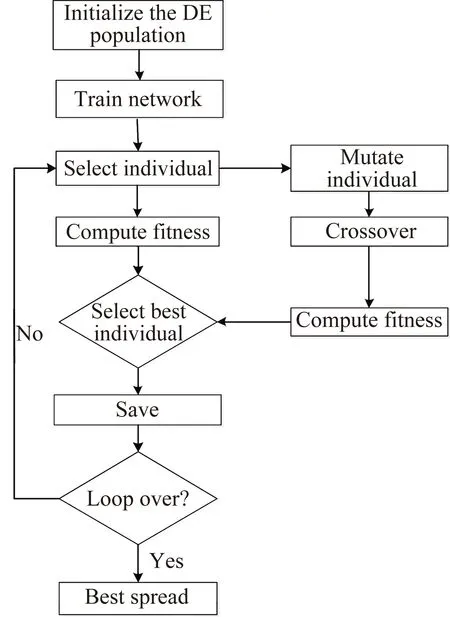
圖2 差分進化算法模型Fig.2 Differential evolution algorithm model

變異步驟：隨機生成三個小于寬度矩陣階數的整數r1、r2、r3。第i+1代跨度矩陣hi+1,n由如下規則算法生成:

其中，hi-1,best為i-1代最優寬度矩陣，ξ為概率密度符合高斯分布的隨機數，hi,n與hi,n-1分別為第i代種群中第n和第n-1個寬度矩陣。

交叉步驟：對于每一個新生成寬度矩陣中的寬度，命令計算機隨機生成一個(0,1)的隨機數,若該隨機數大于交叉因子CR，則原寬度矩陣保持不變；若該隨機數小于CR，則寬度交叉。

在此優化模型中，共4個參數需要設置，分別是變異因子F，交叉因子CR，遺傳代數G與種群數量Size。

1.4 增強模型泛化能力

前人已經針對增加神經網絡泛化能力的工作做出了一系列研究，如Zhao[20]等引入k均值聚類與混合學習算法至神經網絡；Lueng[21]引入梯度下降法去消除亞最優結果，從而優化寬度。Ni[22]等通過在神經網絡中引入驗證算例來增強模型泛化能力。本模型選用引入帶驗證算例的遞歸神經網絡模型來增強模型的泛化能力：訓練信號完成模型訓練后，驗證信號的預測誤差作為差分進化算法的適應度函數，以尋找最優的模型寬度。主要過程如圖3。

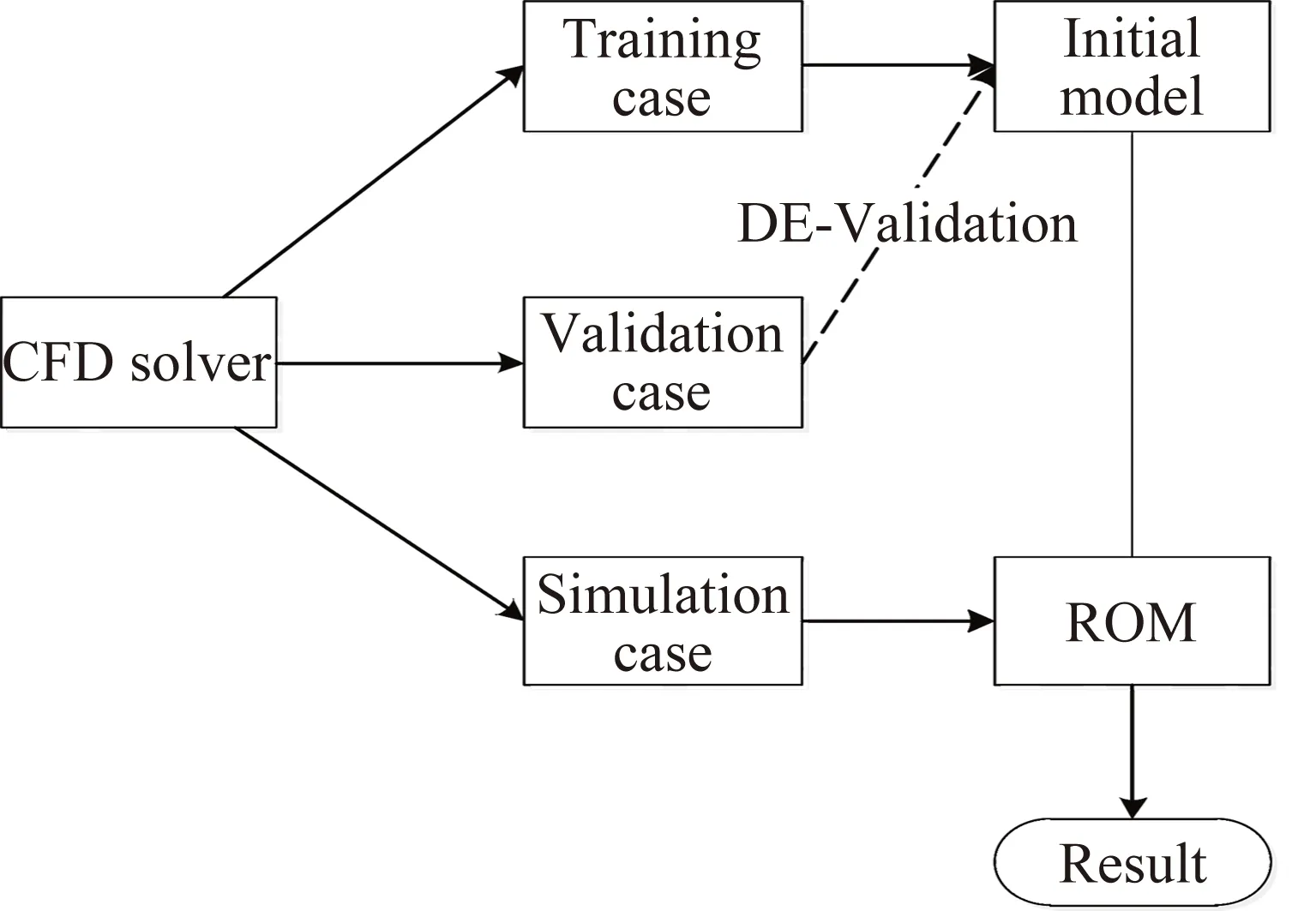
圖3 差分進化算法優化遞歸徑向基函數神經網絡的建模過程Fig.3 Modeling process of the recursive radial basis function neural network optimized by differential evolution algorithm

在圖3中值得注意的是三組樣本含義，如下：

1) 訓練樣本：用于RRBF神經網絡的訓練，確定中心和權值；

2) 驗證樣本：用于尋找并確定最有效的模型。計算適應度函數時，將驗證樣本的輸入信號作為模型輸入，驗證樣本的均方誤差作為差分進化算法的適應度函數，使網絡可以重新調整分散度，并達到驗證誤差最小的狀態，表示模型效果最佳；

3) 預測樣本：以一組新信號構建神經網絡，并用算法中計算出的寬度矩陣作為隱含層中的寬度，檢驗模型的精度以及泛化能力。

這種方法已經被Kou[23]驗證，最后結論為由帶驗證信號方法訓練出來的模型比無驗證信號建模具有更高的精度與泛化能力。

2 算 例

為驗證模型的可行性以及高泛化能力，選取NACA0012翼型作為研究對象，計算在Ma=0.8、翼型繞25%弦長處做俯仰運動的升力系數以及力矩系數。模型采用單輸入單輸出方式，由CFD計算所得的俯仰位移作為函數輸入，通過兩層映射后，分別輸出升力系數與力矩系數。經驗證，此模型比單輸入多輸出模型具有更高計算精度、更小預測誤差、更強的泛化能力。本部分有兩組預測信號，分別為機翼做隨機運動以及周期運動時的位移輸入和升力、力矩系數輸出。樣本信號有1000個樣本點。選取俯仰運動最大幅值A為0.29°、1.15°、2.87°和5.73°(弧度單位分別為0.005、0.02、0.05、0.1)的隨機或簡諧運動數據，數據涵蓋從完全線性、弱非線性到強非線性的特性。預測算例中的簡諧運動選取減縮頻率ks=0.1635，無量綱時間步長為0.4。無量綱時間步長DT計算公式為：

dt為物理時間步長，b為半弦長，a為自由來流聲速。簡諧信號一周期內有60個無量綱時間步長。預測隨機運動時，使用最大俯仰角度為8.59°的信號訓練，并使用最大俯仰角度為0.29°的小幅高頻信號作為驗證信號。經對比，對升力系數而言，延遲階數m、n均為3時得到最優模型；而由于力矩更強的非線性特征，故選擇延遲階數m、n為4。

在構建氣動力模型時，差分進化算法中的變異因子F=0.4，交叉因子CR=0.6，進化代數G=300，種群個數Size=40。在神經網絡模型中每隔20個樣本固定選擇一個中心，可以形成50個中心的模型結構，待優化寬度為50個。

2.1 隨機信號預測結果

預測信號是Ma=0.8時最大俯仰角度為A=5.73°、A=2.87°、A=1.15°、A=0.29°的隨機運動。輸出為升力系數與力矩系數。

2.1.1 訓練信號與驗證信號

圖4為訓練信號，采用NACA0012機翼大幅單自由度隨機運動，最大俯仰角為8.59°，使模型能夠學習結構大振幅非線性時的氣動力，且訓練信號在減縮頻率0至0.4之間具有較強的能量。而圖5展示了兩種驗證信號，分別為小幅高頻運動與大幅隨機運動。模型采用結構小幅高頻信號，以兼顧結構在微幅運動時的線性氣動力信息的學習。驗證信號頻帶更寬，在減縮頻率0至0.8之間具有較強的能量，涵蓋了針對的非定常氣動力問題的頻率。對比組中，模型采用大幅運動信號作為驗證信號，以展示模型在兩種不同驗證信號下的泛化能力。

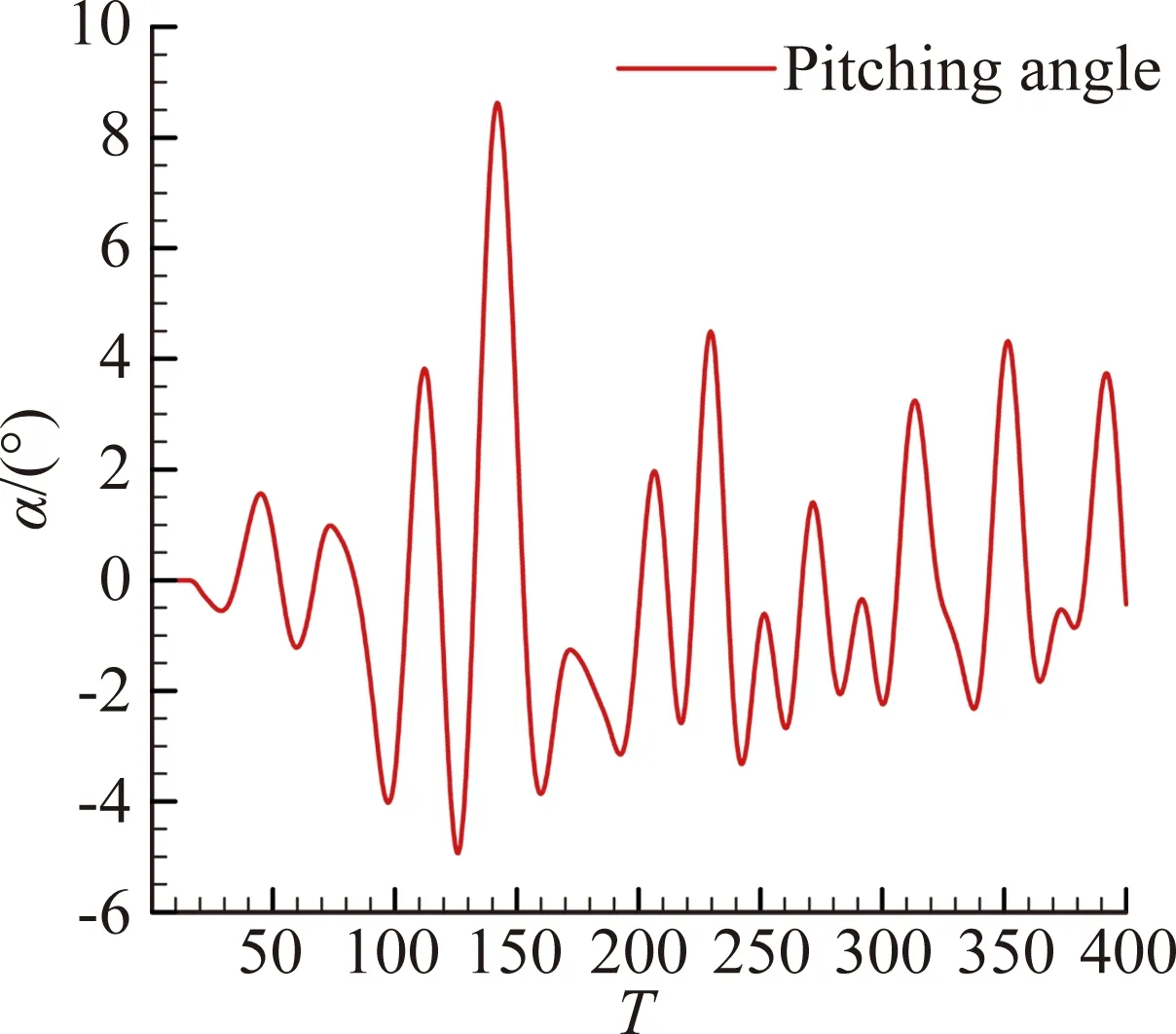
圖4 訓練信號A=8.59°Fig.4 Training signal A=8.59°

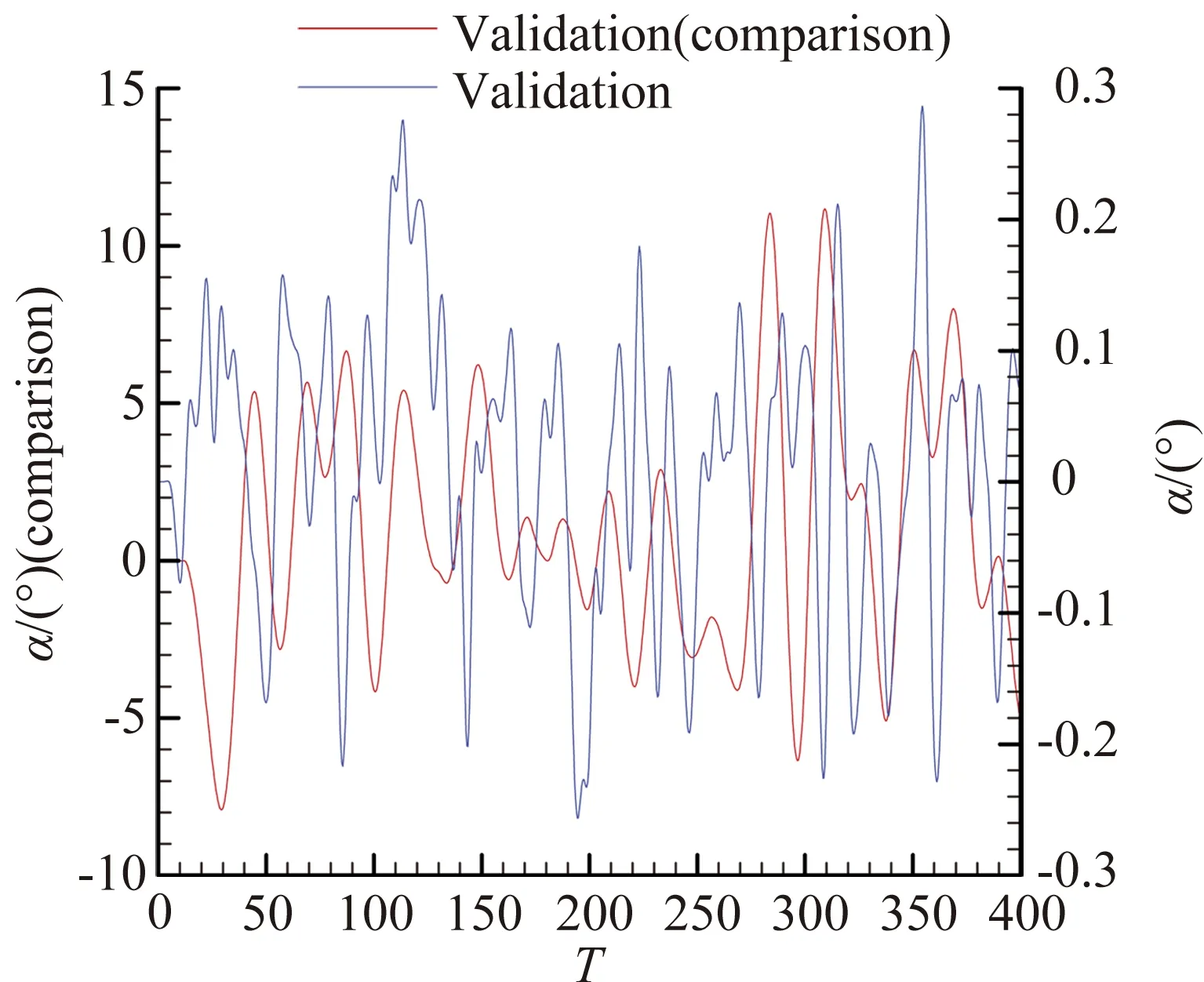
圖5 兩組驗證信號Fig.5 Validation signal and its comparison

圖6、圖7中DE-Simu為用小幅高頻信號作為驗證信號的模型輸出，DE-Simu(comparison)為同等條件下使用大幅信號驗證的模型輸出，文獻[23]中使用的是這種信號。該文獻中并沒有對驗證信號的選取進行研究，而本文將針對不同驗證信號的選取而進行討論。結果選取了用小幅高頻信號驗證與大幅信號驗證對同一預測信號的預測結果作比較，以對比模型選取不同驗證信號而獲得不同的泛化能力。

2.1.2 升力系數預測結果

圖6展示了位移不斷減小的情況下，模型辨識非線性氣動力與線性氣動力的能力。圖6(a)中三條曲線基本吻合，而對比信號組偶爾有辨識不精確的情況，說明了帶小幅高頻驗證信號的DE-RRBFNN模型對非線性氣動力辨識效果更好。隨著信號非線性的減弱，對比信號組逐漸與另外兩組產生了較大偏差，如圖6(b)和圖6(c)。如圖6(d),最終在預測最小俯仰角時，對比信號組曲線已和其他兩條曲線完全分離，而此時引入較小俯仰角驗證信號所預測的結果與CFD計算解吻合得很好。表1給出了隨機運動升力系數相對誤差。

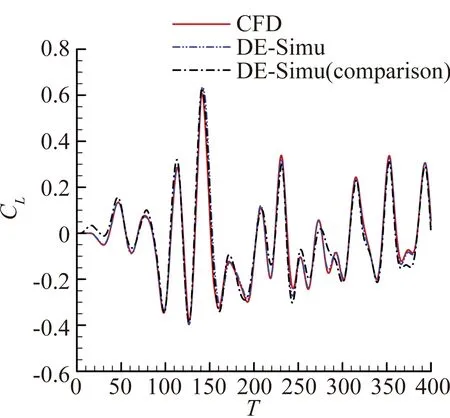
(a) 預測信號A=5.73°

(b) 預測信號A=2.87°

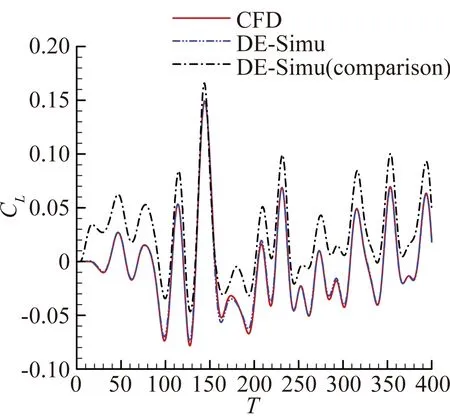
(c) 預測信號A=1.15°

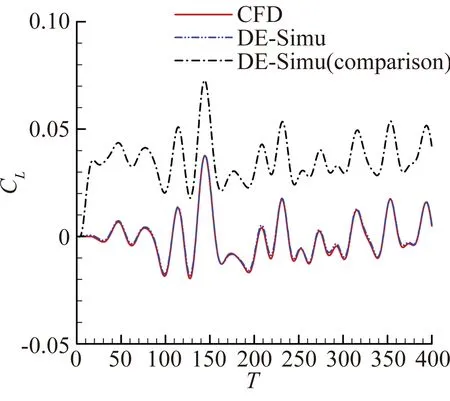
(d) 預測信號A=0.29°

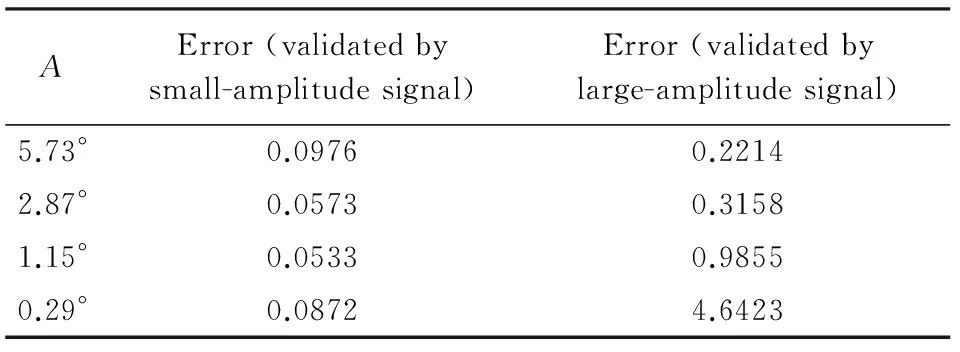
表1 隨機運動升力系數相對誤差Table 1 Relative error of lift coefficient in random motion

2.1.3 力矩系數預測結果

圖7表明了模型對于氣動力矩的辨識能力。與預測升力系數相似，在辨識非線性氣動力時，引入大幅驗證信號和小幅驗證信號的辨識結果沒有明顯差別。而隨著俯仰角的減小，信號線性的增強，引入較小俯仰角的模型具有了較大的精度，這點從圖7(d)以及表2的內容中可以看出。值得注意的是，在預測較大幅度的運動時，驗證信號的不同對模型精度并沒有明顯改變。但是在辨識小運動幅度的氣動力矩時，可以體現出引入較小俯仰角驗證信號的優勢。

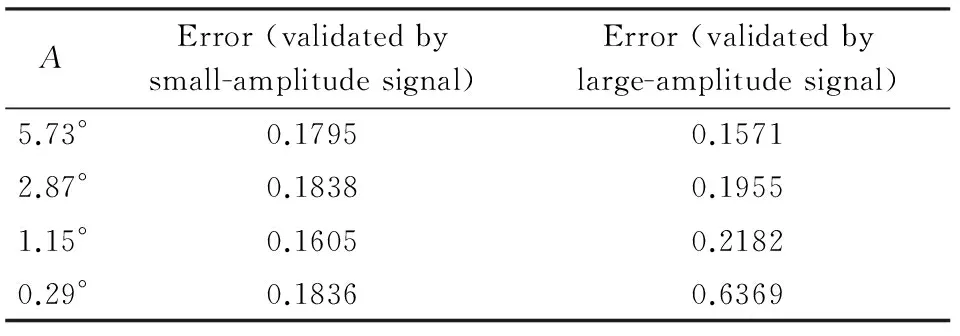
表2 隨機運動力矩系數相對誤差Table 2 Relative error of moment coefficient in random motion

通過以上可以發現使用小幅高頻驗證信號所得到的模型要優于使用大幅驗證信號所得的模型。

通過對隨機運動的氣動力預測可以得出：引入小幅驗證信號對增強神經網絡模型辨識線性氣動力系數以及力矩系數的能力有很大幫助，進一步的增加了模型對不同運動幅度信號的泛化能力。

2.2 簡諧信號預測結果

本小節采用Ma=0.8時減縮頻率ks=0.1635的簡諧運動進行模型測試，振幅分別為A=5.73°、A=2.87°、A=1.15°、A=0.29°。輸出為升力系數與力矩系數，預測簡諧運動的訓練信號與之前給出的訓練信號相同。

圖8、圖9展現了模型對簡諧信號的預測能力。與辨識非線性氣動力結果類似，圖8(a)中兩模型在辨識大幅信號時沒有明顯區別。隨著信號振幅的減小，引入小幅驗證信號的優勢可以明顯體現。從圖8(b)至圖8(d)可以看出小幅驗證信號所辨識的結果與CFD計算解更加貼合。而圖8(a)的遲滯環滯回空間小是因為該狀態靠近做功轉換臨界點，振幅小于該狀態時，遲滯環為逆時針，氣動力做負功；振幅大于臨界點時，遲滯環變為順時針，氣動力做正功。臨界點狀態附近的狀態由于各種外力因素的作用而滯回空間小，但并非接近定常狀態。對于辨識的力矩系數，從圖9(a)至圖9(d)中可以看出，隨著振幅減小，引入小幅驗證信號的結果要明顯優于大幅驗證信號。

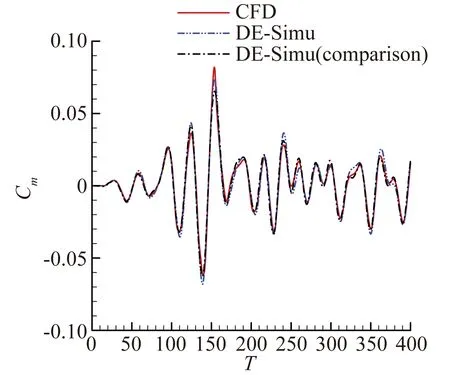
(a) 預測信號A=5.73°

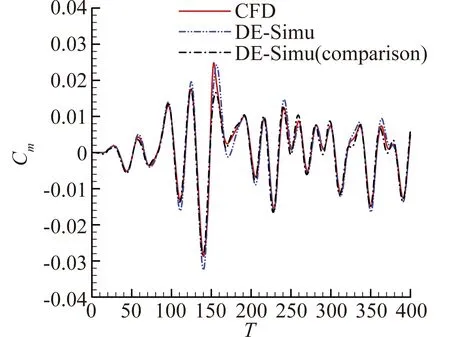
(b) 預測信號A=2.87°

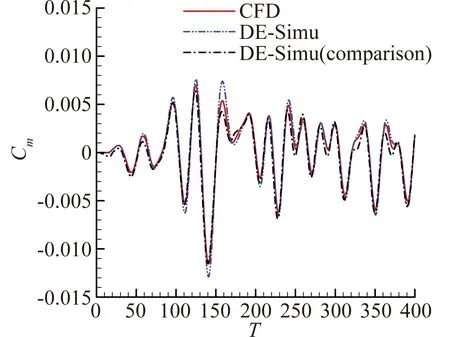
(c) 預測信號A=1.15°

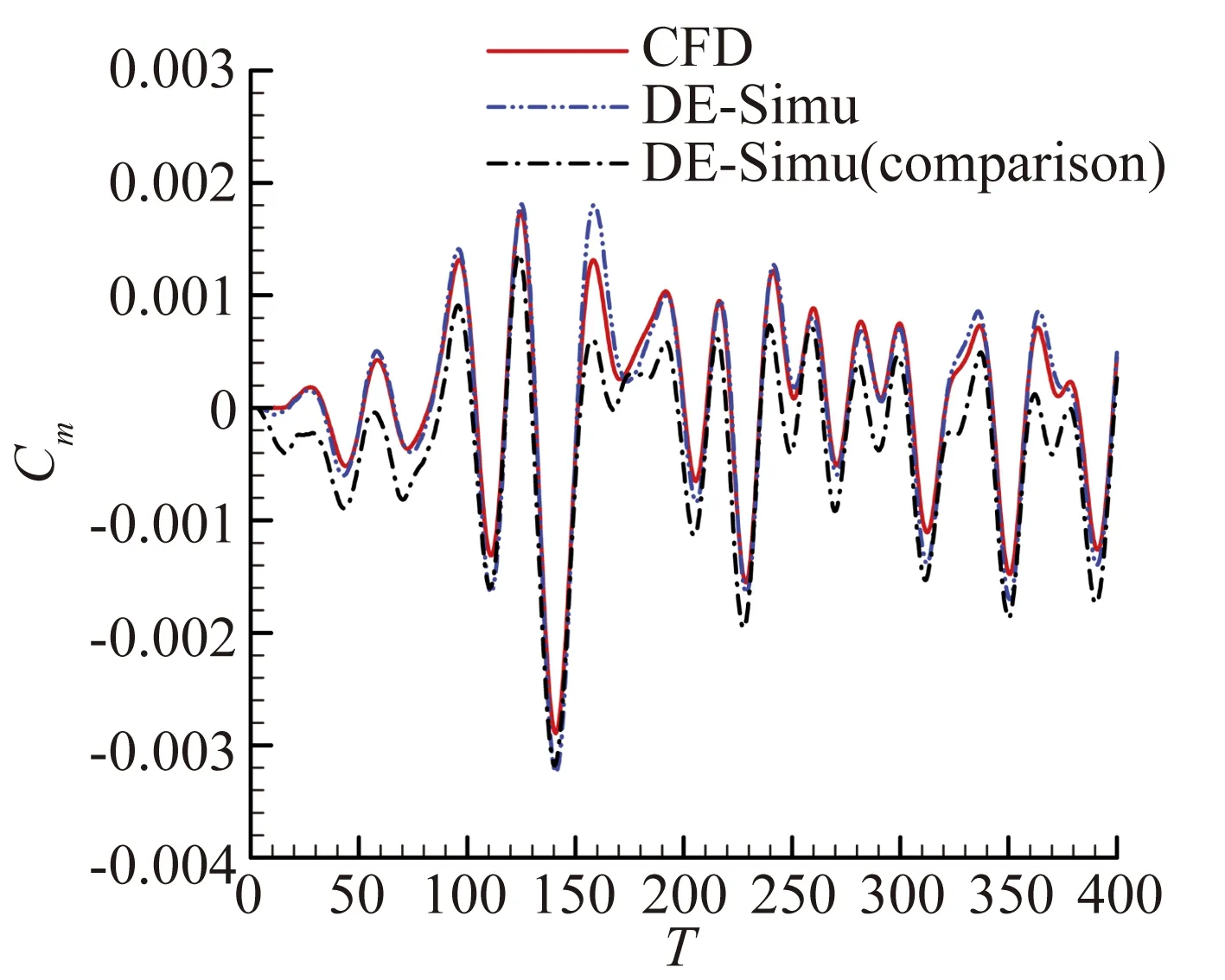
(d) 預測信號A=0.29°

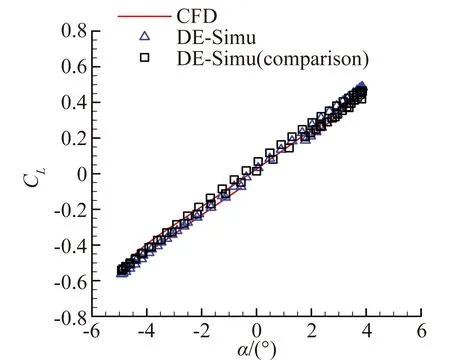
(a) 預測信號A=5.73°

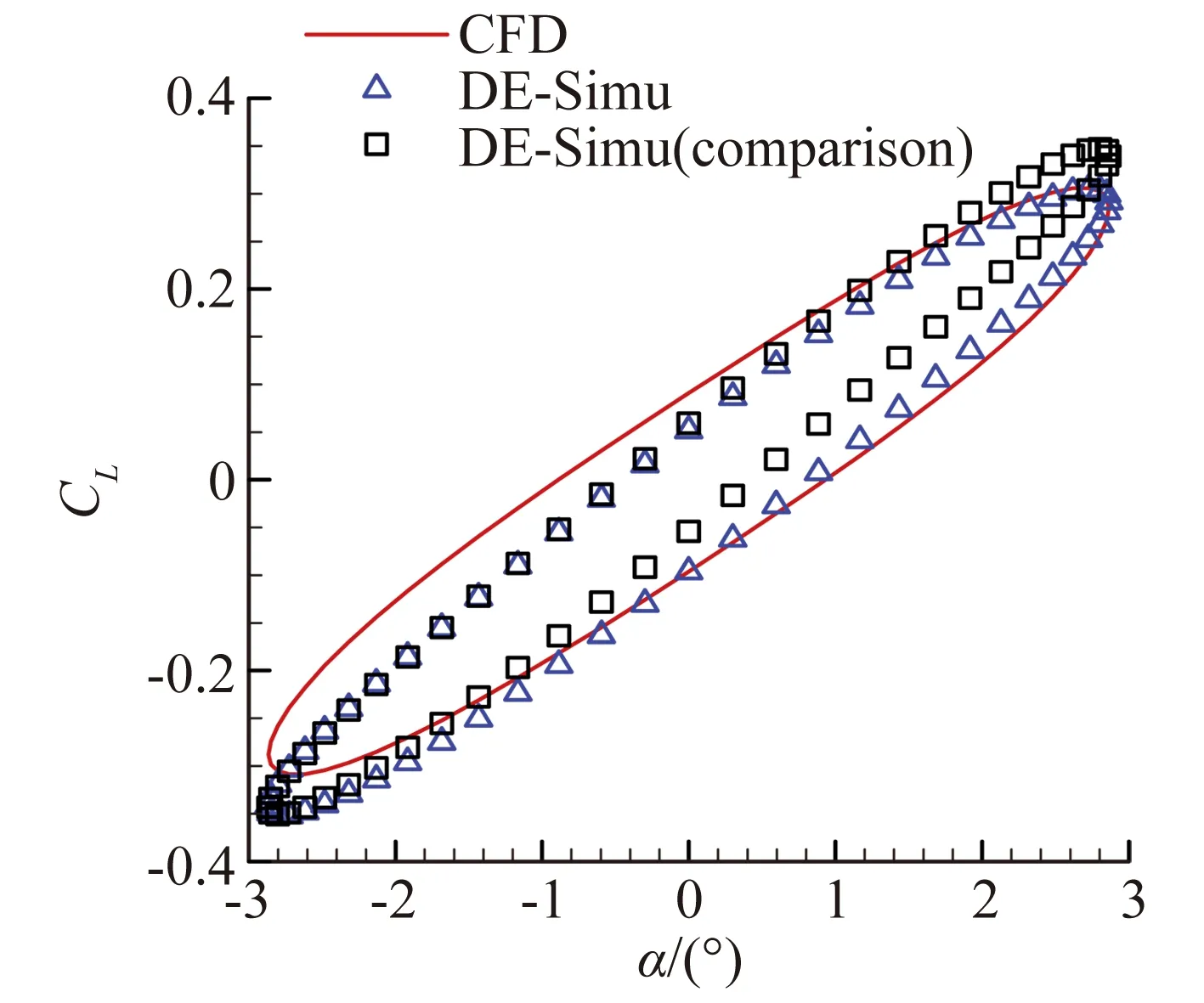
(b) 預測信號A=2.87°

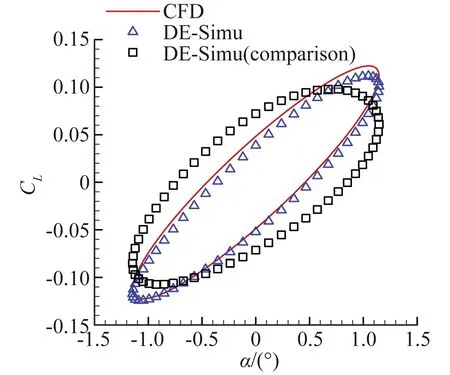
(c) 預測信號A=1.15°

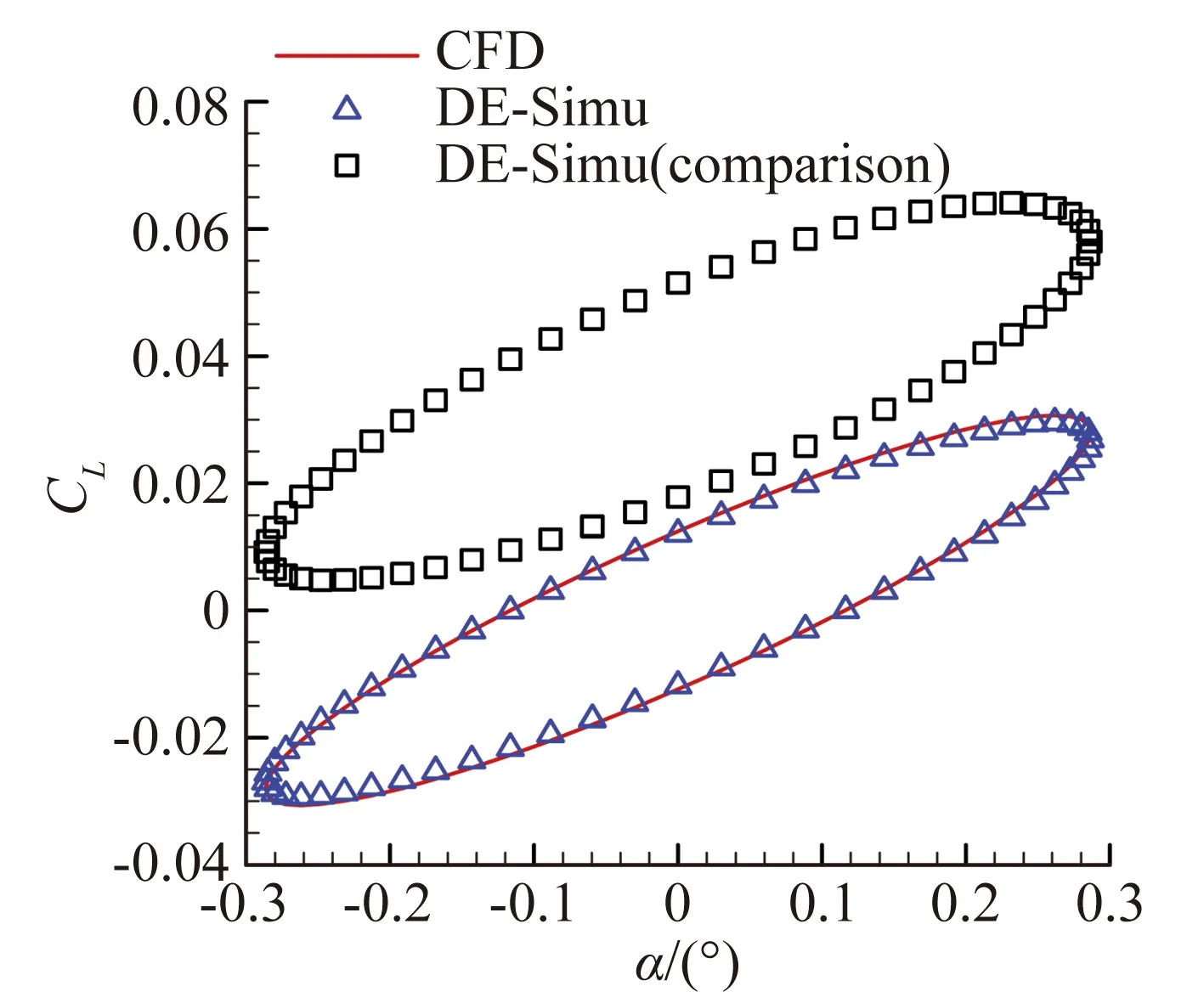
(d) 預測信號A=0.29°

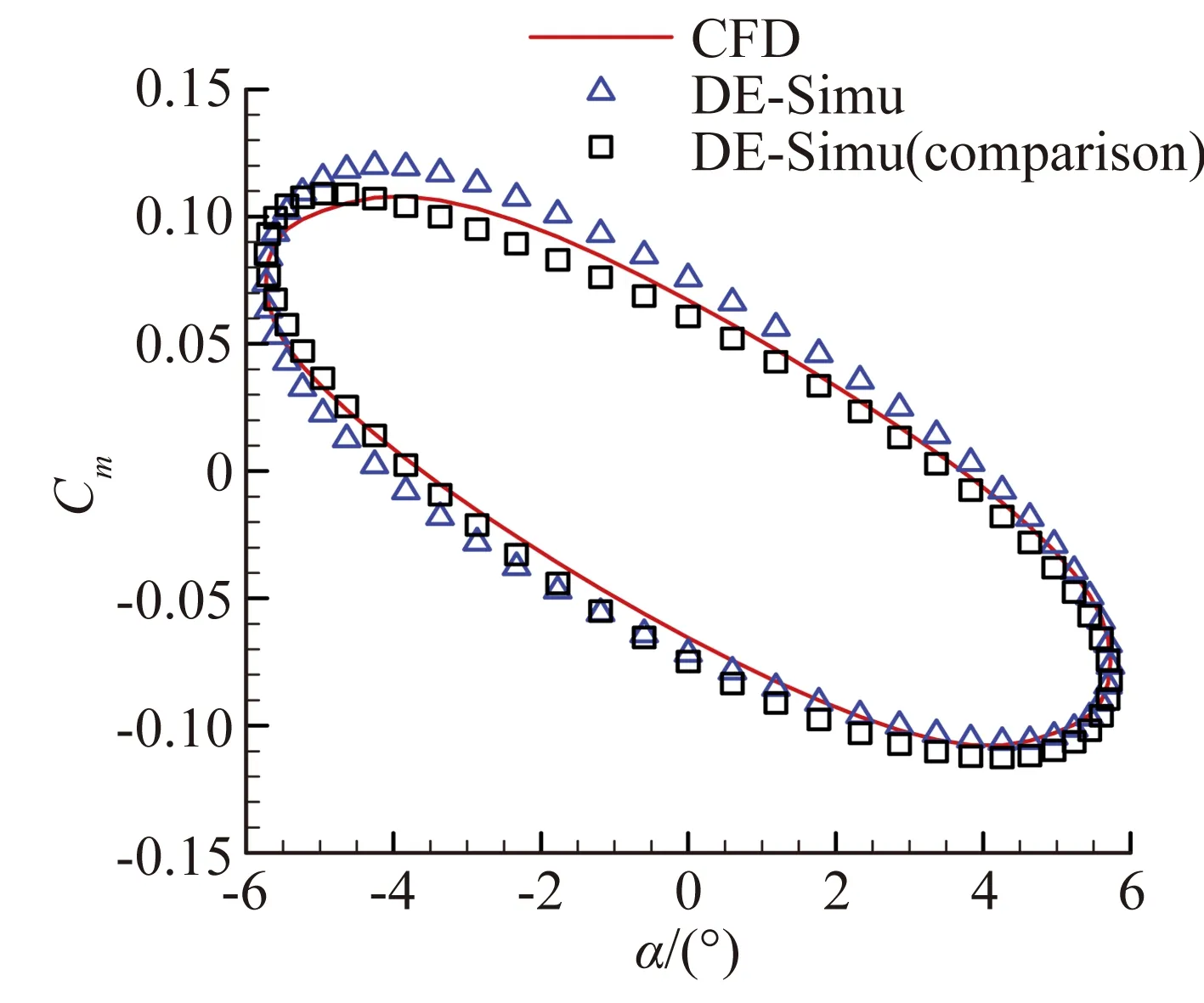
(a) 預測信號A=5.73°

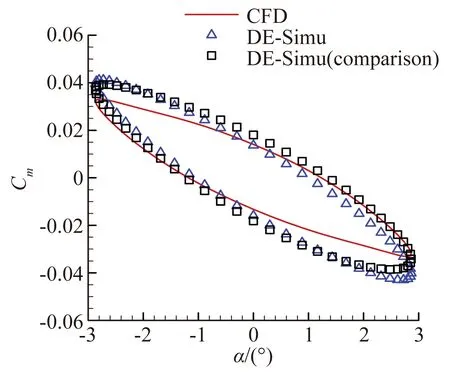
(b) 預測信號A=2.87°

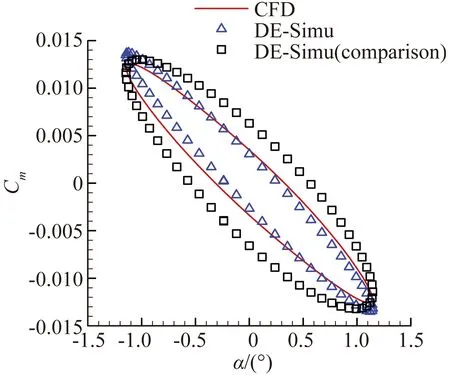
(c) 預測信號A=1.15°

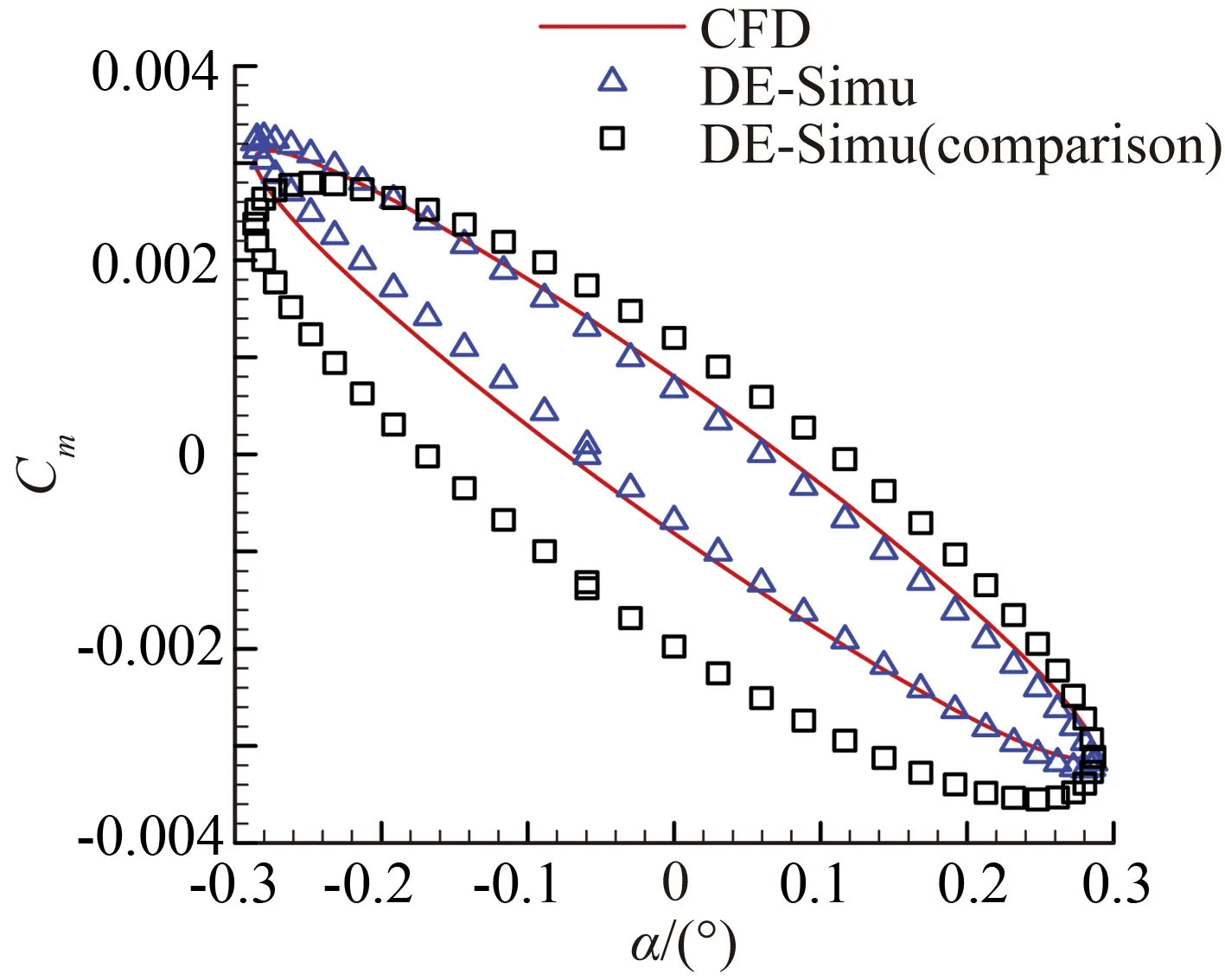
(d) 預測信號A=0.29°

表3、表4分別為簡諧運動升力系數和力矩系數相對誤差。

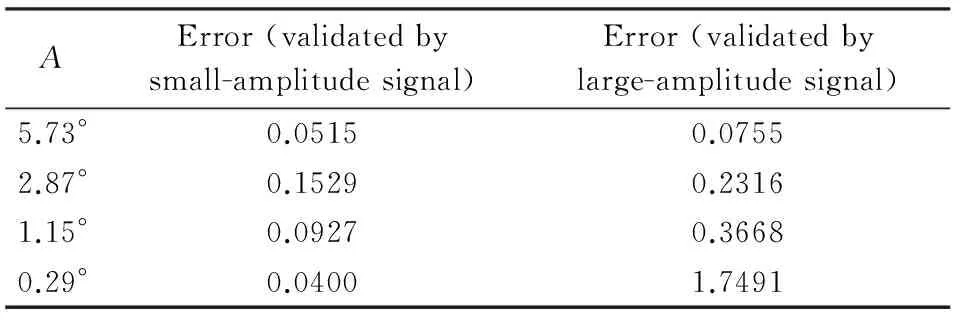
表3 簡諧運動升力系數相對誤差Table 3 Relative error of lift coefficient in harmonic motion

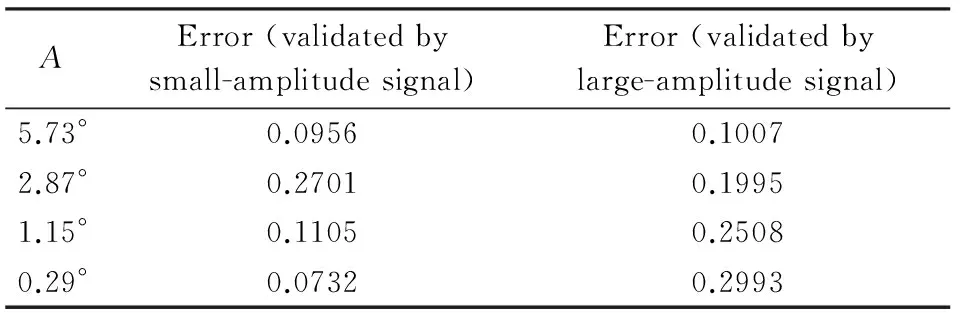
表4 簡諧運動力矩系數相對誤差Table 4 Relative error of moment coefficient in harmonic motion

綜上，使用小幅高頻信號作為驗證信號的模型都具有與用大幅驗證信號相近或更高的輸出精度。尤其是在小幅線性運動預測時，使用小幅驗證信號的優勢極為突出。從寬度角度解釋，引入的小幅高頻驗證信號調整了神經網絡模型中隱含層中的寬度，即隱含層中寬度的確定不單單依賴于大幅訓練信號的特性，同時也依賴于驗證信號中小幅信號的特性，兩者一同決定在給定中心下的最優寬度。所以最后小幅驗證信號的結果優于大幅驗證信號，這種建模方法進一步增強了模型的泛化能力。

3 結 論

本文發展了一種基于CFD的RRBF神經網絡氣動力模型，通過引入驗證信號改進了模型泛化能力。該模型以翼型俯仰運動的位移為輸入，分別輸出升力系數或力矩系數，并引入輸出反饋以體現非定常流場的動態效應。神經網絡采用固定間隔的中心選擇，并且使用差分進化算法優化每個神經元的寬度以調整模型的泛化能力。算法優化目標為使得驗證信號的預測精度最高。預測算例采用了跨聲速下NACA0012翼型的隨機和簡諧俯仰運動，以對比不同驗證信號對模型精度的影響，及這種模型對于不同振幅下非定常流場動態特征的泛化能力。算例表明當采用小幅高頻驗證信號時，模型對于大幅運動下的強非線性特征和小擾動下的動態線性特點均具有更高的預測精度，因此發展的這種DE-RRBFNN模型總體上能夠把握非定常氣動力的主要特征，且耗時遠低于CFD計算。

[1]Dowell E H. Eigenmode analysis in unsteady aerodynamics: reduced order models[J]. AIAA Journal, 1996, 34(8): 1578-1583.

[2]Silva W A. Identification of linear and nonlinear aerodynamic impulse responses using digital filter techniques. AIAA-97-3712[R]. Reston: AIAA, 1997.

[3]Zhang W W, Ye Z Y. On unsteady aerodynamic modeling based on CFD technique and its applications on aeroelastic analysis[J]. Advances in Mechanics, 2008, 38(1): 77-86. (in Chinese)張偉偉, 葉正寅. 基于CFD的氣動力建模及其在氣動彈性中的應用[J]. 力學進展, 2008, 38(1): 77-86.

[4]Hall K C, Thomas J P, Dowell E H. Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows[J]. AIAA Journal, 2000, 38(10): 1853-1862.

[5]Raveh D E. Reduced-order models for nonlinear unsteady aerodynamics[J]. AIAA Journal, 2001, 39(8): 1417-1429.

[6]Zhang W W, Ye Z Y, Zhang C A. ROM based aeroservoelastic analysis in transonic flow[J]. Journal of Aircraft, 2009, 46(6): 2187-2183.

[7]Glaz B, Liu L, Friedmann P P. Reduced order nonlinear unsteady aerodynamic modeling using a surrogate based recurrence framework[J]. AIAA Journal, 2010, 48(10): 2418-2429.

[8]Marquez F D, Anderson J. Identification and prediction of unsteady transonic aerodynamic loads by multi-layer functionals[J]. Journal of Fluids and Structures, 2001, 15(1): 83-106.

[9]Thomas J P, Dowell E H, Hall K C. Nonlinear inviscid aerodynamic effects on transonic divergence, flutter, and limit-cycle oscillations[J]. AIAA Journal, 2002, 40(4): 638-646.

[10]Lindhorst K, Haupt M C, Horst P. Efficient surrogate modelling of nonlinear aerodynamics in aerostructural coupling schemes[J]. AIAA Journal, 2014, 52(9): 1952-1966.

[11]Ghoreyshi M, Jirasek A, Cummings R M. Computational approximation of nonlinear unsteady aerodynamics using an aerodynamic model hierarchy[J]. Aerospace Science and Technology, 2013, 28(1): 133-144.

[12]Shi Z W, Ni F Y, Chen Y L. The state-space models based on two-steps linear regression method[J]. Acta Aerodynamica Sinica, 2013, 31(6): 699-703. (in Chinese)史志偉, 倪芳原, 陳永亮. 基于兩步線性回歸的狀態空間模型建立與驗證[J]. 空氣動力學學報, 2013, 31(6): 699-703.

[13]Zhang W W, Wang B B, Ye Z Y. Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced-order models[J]. AIAA Journal, 2012, 50(5): 1019-1028.

[14]Wang B B, Zhang W W, Ye Z Y. Unsteady nonlinear aerodynamics identification based on Neural Network model[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1379-1387. (in Chinese)王博斌, 張偉偉, 葉正寅. 基于神經網絡模型的動態非線性氣動力辨識方法[J]. 航空學報, 2010, 31(7): 1379-1387.

[15]Du H P, Zhang N. Time series prediction using evolving radial basis function networks with new encoding scheme[J]. Neurocomputing, 2008, 71(7-9): 1388-1400.

[16]Kurkova V, Sanguineti M. Learning with generalization capability by kernel methods of bounded complexity[J]. Journal of Complexity, 2005, 21(3): 350-367.

[17]Kou J Q, Zhang W W, Ye Z Y. Dynamic nonlinear aerodynamics modeling method based on layered method[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(12): 3785-3797. (in Chinese)寇家慶, 張偉偉, 葉正寅. 基于分層思路的動態非線性氣動力建模方法[J]. 航空學報, 2015, 36(12): 3785-3797.

[18]Kou J Q, Zhang W W. Research on the effects of basis function widths of aerodynamic modeling based on recursive RBF neural network[J]. Advances in Aeronautical Science and Engineering, 2015, 6(3): 261-270. (in Chinese)寇家慶, 張偉偉. 基函數寬度對遞歸RBF神經網絡氣動力模型精度的影響研究[J]. 航空工程進展, 2015, 6(3): 261-270.

[19]Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.

[20]Zhao Z Q, Huang D S. A mended hybrid learning algorithm for radial basis function neural networks to improve generalization capability[J]. Applied Mathematical Modelling, 2007, 31(7): 1271-1281.

[21]Leung C, Chow T W S. Adaptive regularization parameter selection method for enhancing generalization capability of neural networks[J]. Artificial Intelligence, 1999, 107(2): 347-356.

[22]Ni Y Q, Zhou H F, Ko J M. Generalization capability of neural network models for temperature-frequency correlation using monitoring data[J]. Journal of Structural Engineering, 2009, 135(10): 1290-1300.

[23]Kou J Q, Zhang W W. An approach to enhance the generalization capability of nonlinear aerodynamic reduced-order models[J]. Aerospace Science and Technology, 2016, 49(1): 197-208.

A reduced-order aerodynamic model with high generalization capability based on neural network

Yin Minglang1,2, Kou Jiaqing1, Zhang Weiwei1,*

(1.NationalKeyLaboratoryofScienceandTechnologyonAerodynamicDesignandResearch,NorthwesternPolytechnicalUniversity,Xi’an710072,China;2.SchoolofEngineering,BrownUniversity,Providence02906,TheUnitedStatesofAmerica)

Generalization capability of neural network model names the prediction ability of the model to new input signal. However, current nonlinear aerodynamic models based on neural network usually lack such capability. To cover this shortage, a CFD-based aerodynamic model using differential evolution with validation signal is proposed and improved to predict transonic aerodynamic load. To minimize root mean square error of validation signal, the widths of neural centers in hidden layers are optimized by introducing differential evolution in this recursive radial basis function neural network. Training signal is large-amplitude displacement of that structural, while the validation signal is small-amplitude structural displacement. The results not only indicate the shorter calculating time of this reduced-order model than that of full-order numerical calculation, but a higher generalization capability of the model under various frequencies and amplitudes due to the introduction of small-amplitude validation signal.

unsteady aerodynamic load; reduced-order model; neural network; generalization capability; validation signal

0258-1825(2017)02-0205-09

2015-12-23;

2016-06-25

國家自然科學基金(11572252);國家自然科學基金優秀青年科學基金(11622220);國家高等學校學科創新引智計劃(“111”計劃)(B17037)

尹明朗(1994-),男,北京人,碩士研究生,研究方向:氣動力建模. E-mail: minglang_yin@brown.edu

張偉偉*,教授,研究方向:氣動彈性力學. E-mail: aeroelastic@nwpu.edu.cn

尹明朗, 寇家慶, 張偉偉. 一種高泛化能力的神經網絡氣動力降階模型[J]. 空氣動力學學報, 2017, 35(2): 205-213.

10.7638/kqdlxxb-2015.0210 Yin M L, Kou J Q, Zhang W W. A reduced-order aerodynamic model with high generalization capability based on neural network[J]. Acta Aerodynamica Sinica, 2017, 35(2): 205-213.

V211.1+5

A doi: 10.7638/kqdlxxb-2015.0210