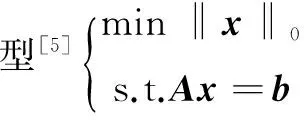基于擬牛頓法的梯度追蹤算法研究

劉 艷,李 雷

(南京郵電大學(xué) 非結(jié)構(gòu)化數(shù)據(jù)計算理論與應(yīng)用研究中心，江蘇 南京 210046)

基于擬牛頓法的梯度追蹤算法研究

劉 艷,李 雷

(南京郵電大學(xué) 非結(jié)構(gòu)化數(shù)據(jù)計算理論與應(yīng)用研究中心，江蘇 南京 210046)

為了解決傳統(tǒng)迭代算法中需要計算正交投影的問題，將擬牛頓法與梯度追蹤算法(Gradient Pursuit)相結(jié)合，提出了基于擬牛頓法的梯度追蹤算法(Quasi-Newton Method based Gradient Pursuit,QNMGP)。擬牛頓法是解決無約束最優(yōu)化問題的有效方法，其避免了牛頓法需要求解Hesse矩陣的問題，降低了計算量，提高了收斂速度，新提出的算法通過限域擬牛頓法來求解更新方向，并將其運用到梯度追蹤算法中。為驗證新提出算法的可行性與有效性，基于MATLAB仿真平臺，從重構(gòu)時間、均方誤差和峰值信噪比三個方面對QNMGP算法與其他貪婪算法進(jìn)行了仿真對比實驗驗證。仿真實驗結(jié)果表明，在同等的測試環(huán)境下，新提出的QNMGP算法重構(gòu)效果遠(yuǎn)優(yōu)于其他算法，且在重構(gòu)時間上也具有一定的優(yōu)勢。

擬牛頓法；梯度追蹤；最優(yōu)化問題；重構(gòu)算法

1 概 述

壓縮感知[1-3](Compressive Sensing,CS)理論是近年來出現(xiàn)的一種新型壓縮采樣方法。該理論指出，如果信號可壓縮或者在某個變換域上是稀疏的，就能用一個與變換基不相關(guān)的觀測矩陣將高維信號投影到一個低維空間上，接著通過求解一個優(yōu)化問題就能夠從這些少量的投影中高概率地重構(gòu)出原信號。

假設(shè)b∈Rn為一個已知的向量，A為m×n維的觀測矩陣且滿足m

b=Ax+ε

(1)

由于貪婪迭代算法的迭代過程比較簡單，因此目前應(yīng)用比較廣泛，其主要是解決式(2)這類子空間優(yōu)化問題，但是此類算法都需要通過計算量很大的正交投影來估計信號，在一定程度上增加了重構(gòu)計算量，降低了收斂速度。……