基于MATLAB對“Y型”果樹振動共振頻率的研究

魏庭鵬++王春耀++閔磊++呂夢璐

摘要：為了研究果樹振動時樹干、樹枝的加速度動態響應，獲得最優共振頻率的階數、數值、區間，得出果樹振動的最優激振參數，為林果振動采摘收獲機的參數優化提供理論基礎，將樹干-樹枝力學模型簡化為雙自由度的質量-剛度-阻尼力學模型，建立振動方程，對方程進行仿真、運算，并結合試驗所得結果進行對比分析。結果顯示，仿真與試驗中，整個果樹共出現了6階共振頻率，其中1階、2階、3階最為明顯，分別約為1.72、4.18、7.72 Hz；同時，整個果樹的共振頻率始終都是在0～12、17～25 Hz這2個區間內。表明果樹振動落果過程中，0～12、17～25 Hz這2個頻率區間可作為整個果樹振動落果的參考頻率區間。其中，1.72、4.18、7.72 Hz可作為整個果樹振動落果的首選參考頻率；激振載荷數值增加，果樹共振頻率的階數、區間、數值并不會隨之改變，但樹干、樹枝的加速度響應幅值是逐漸增加的。

關鍵詞：果樹；動態響應；共振頻率；激振參數；采摘收獲機

中圖分類號： S225. 93文獻標志碼： A

文章編號：1002-1302（2017）03-0169-03

收稿日期：2015-09-06

基金項目：國家自然科學基金（編號：51465054）。

作者簡介：魏庭鵬（1990—），男，江蘇儀征人，碩士研究生，主要從事機械系統動力學研究。E-mail：weitingpeng100@126.com。

通信作者：王春耀，教授，碩士生導師，主要從事力學研究。E-mail：wangchun_yao@126.com。

林果產業作為新疆的特色性產業，創造了可觀的經濟效益，然而由于種植面積廣、采收周期短、勞動力緊缺等問題，常常使得林果采摘不及時，從而降低了產量，影響了果農的收入[1-2]；與傳統的人工采摘方式相比，機械振動采摘方式具有效率高、成本低的顯著優勢。近年來，針對林果機械振動采摘的研究，國內外的眾多學者取得了一定的成果，如Torregrosa等研發了一種振搖樹干式杏子收獲機，并對其進行了試驗研究，結果表明當激振頻率為15 Hz時，收獲效率最高，達72%[3]。在國內，陳度等分別采用正弦式和沖擊式2種激振方式，對櫻桃進行了振動采收試驗，通過對比結果得出，樹枝在沖擊式激振下的動態響應要大于在正弦式激振下的動態響應[4]。王業成等通過振動采收試驗分析了激振頻率、振幅、激振位置對黑加侖葡萄落果率的影響，結果表明影響落果率的因素從大到小的順序依次為頻率、振幅、激振位置[5]。

針對果樹力學模型的建立，Láng做了一系列的研究，最終得出一些重要結論。他指出，首先果樹在振動時，樹干的運動與各分枝的運動是相互獨立的，即樹干在分叉處的上下部分具有良好的線性關系；其次，在只考慮果樹的結構阻尼，忽略黏性阻尼的前提下，將樹干-樹枝力學模型簡化為雙自由度的質量-剛度-阻尼力學模型時，較為準確[6-8]。然而，針對建立的模型，Láng并未對其進行進一步的探究，在其建立的力學模型基礎上，本試驗進一步研究振動時樹干、樹枝的加速度動態響應，獲得最優共振頻率的階數、數值、區間，并且通過試驗驗證，最終得出果樹振動的最優激振參數，為林果振動采摘收獲機的參數優化提供參考。

1樹干-樹枝的建模與仿真

1.1建立樹干-樹枝模型

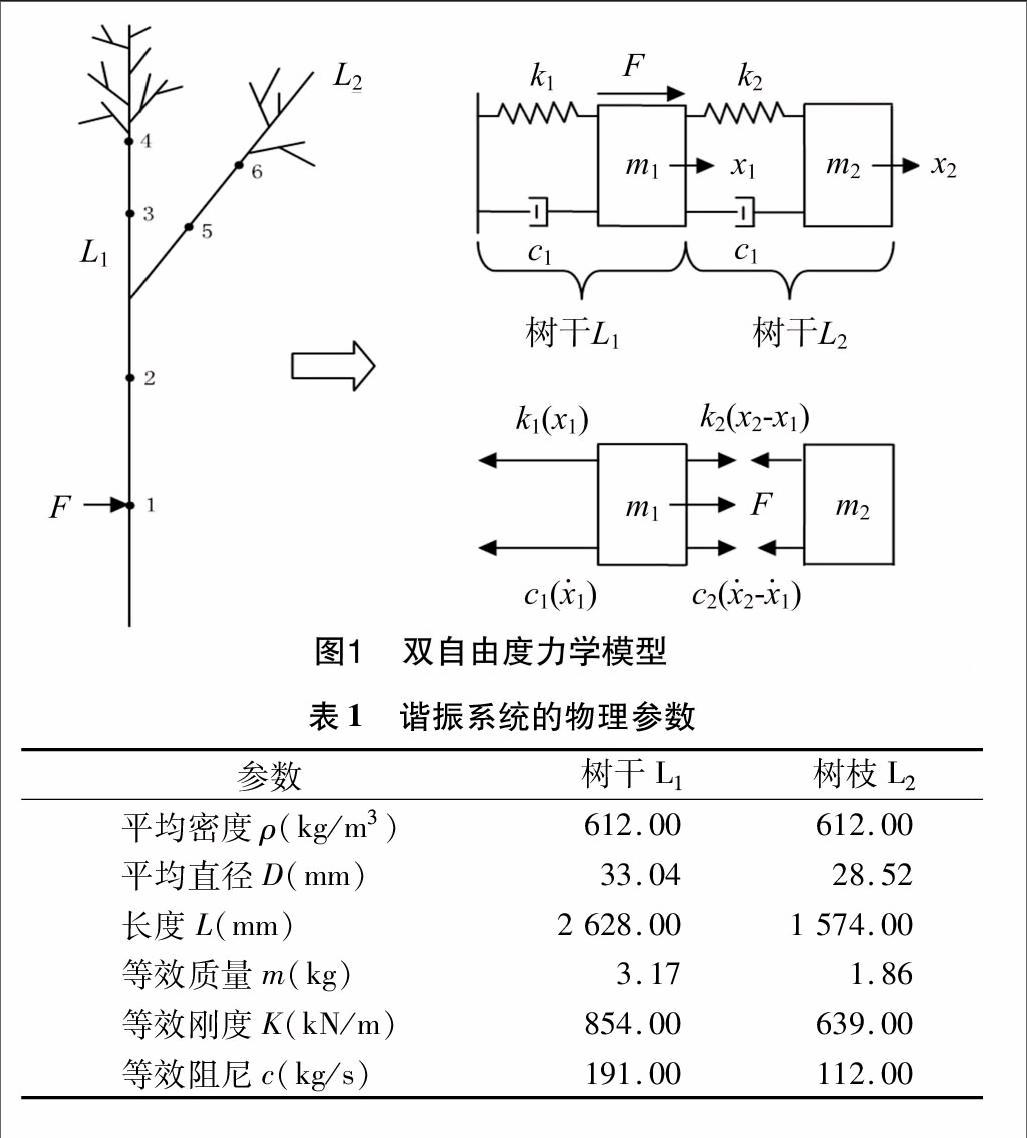
選取生物形態較規則、分枝與樹干盡量在同一平面內的“Y型”海棠果樹樹枝作為研究對象，針對Láng提出的力學模型，如圖1所示，[JP2]忽略樹干、樹枝末端少量的嫩枝、嫩葉的重力，將樹干、樹枝各自等效為1個集中質量塊，之間視為以彈簧件、阻尼器彈性連接。因此，在振動過程中，樹枝L2對樹干L1[JP2]的作用，可以看作質量塊m2在彈簧件k2和阻尼器c2作用下的諧振系統對質量塊m1的作用，取點1、2、3、4、5、6作為試驗的監測點，其中，在距離固定端部0.5 m處取點1，分別依次施加5、7、9 g的激振載荷，諧振系統相關的物理參數如表1所示。

1.2仿真運算

依據建立的雙自由度力學模型，物體離開平衡位置的位移用x1、x2表示，2個質量塊在水平方向的受力如圖1中所示，依據力的平衡條件并加以整理得公式（1）：

[JZ（][JB（{]m1[KG-*5]x[DD（-1*2][HT6]¨[DD）]1+（c1+c2）[KG-*5]x[DD（-1*2][HT6][DD）]1-c2[KG-*5]x[DD（-1*2][HT6][DD）]2+（k1+k2）x1-k2x2=Fm2[KG-*5]x[DD（-1*2][HT6]¨[DD）]2-c2[KG-*5]x[DD（-1*2][HT6][DD）]1+c2[KG-*5]x[DD（-1*2][HT6][DD）]2-k2x1+k2x2=0[JB）]。[JZ）][JY]（1）

將公式（1）寫成矩陣形式見公式（2）：

[HT9.，8.][JP3][JB（（]m100m2[JB））][JB（（][KG-*5]x[DD（-1*2][HT6]¨[DD）]1[KG-*5]x[DD（-1*2][HT6]¨[DD）]2[JB））]+[JB（（]c1+c2-c2-c2c2[JB））][JB（（][KG-*5]x[DD（-1*2][HT6][DD）]1[KG-*5]x[DD（-1*2][HT6][DD）]2[JB））]+[JB（（]k1+k2-k2-k2k2[JB））][JB（（]x1x2[JB））]=[JB（（]F0[JB））][JP]。[JY]（2）

最終可得雙自由度系統的運動微分方程[9-11]，見公式（3）：

[JZ（][KG-*5][WTHX][STHX]M[DD（-*2][HT6]→[DD）][KG*5]x[DD（-1*2][HT6]¨[DD）]+[KG-*5][WTHX][STHX]C[DD（-*2][HT6]→[DD）][KG-*5]x[DD（-1*2][HT6][DD）]+[KG-*5][WTHX][STHX]K[DD（-*2][HT6]→[DD）]x=[KG-*5][WTHX][STHX]f[DD（-*2][HT6]→[DD）][JZ）][JY]（3）

這是一個二階常系數線性非其次微分方程組，式中：

[JZ][WTHX][STHX]M[DD（-*2][HT6]→[DD）]=[JB（（]m100m2[JB））]，[KG-*5][WTHX][STHX]C[DD（-*2][HT6]→[DD）]=[JB（（]c1+c2-c2-c2c2[JB））]

[JZ（][KG-*5][WTHX][STHX]K[DD（-*2][HT6]→[DD）]=[JB（（]k1+k2-k2-k2k2[JB））]，[KG-*5]f[DD（-*2][HT6]→[DD）]=[JB（（]F0[JB））]。[JZ）][JY]（4）

分別為系統的質量矩陣、阻尼矩陣、剛度矩陣和外部載荷矩陣。

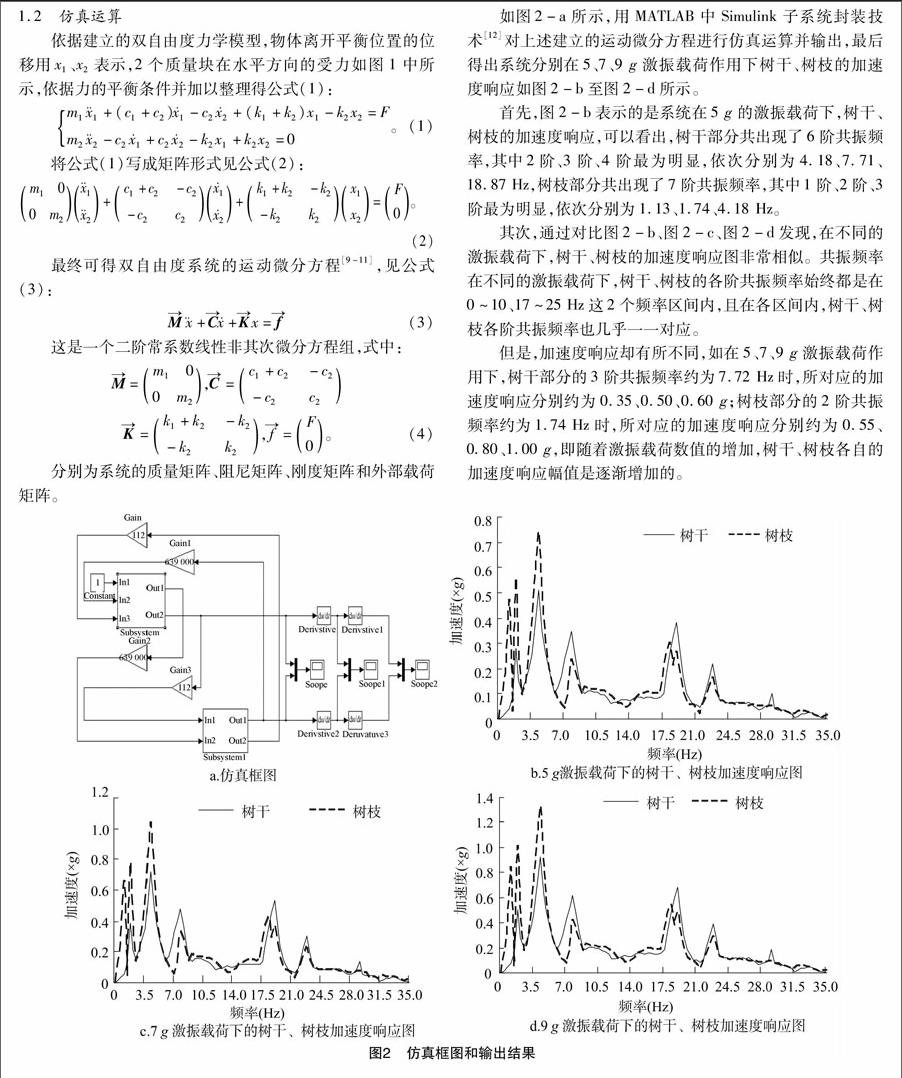
如圖2-a所示，用MATLAB中Simulink子系統封裝技術[12]對上述建立的運動微分方程進行仿真運算并輸出，最后得出系統分別在5、7、9 g激振載荷作用下樹干、樹枝的加速度響應如圖2-b至圖2-d所示。

首先，圖2-b表示的是系統在5 g的激振載荷下，樹干、樹枝的加速度響應，可以看出，樹干部分共出現了6階共振頻率，其中2階、3階、4階最為明顯，依次分別為4.18、7.71、18.87 Hz，樹枝部分共出現了7階共振頻率，其中1階、2階、3階最為明顯，依次分別為1.13、1.74、4.18 Hz。

其次，通過對比圖2-b、圖2-c、圖2-d發現，在不同的激振載荷下，樹干、樹枝的加速度響應圖非常相似。共振頻率在不同的激振載荷下，樹干、樹枝的各階共振頻率始終都是在0～10、17～25 Hz這2個頻率區間內，且在各區間內，樹干、樹枝各階共振頻率也幾乎一一對應。

但是，加速度響應卻有所不同，如在5、7、9 g激振載荷作用下，樹干部分的3階共振頻率約為7.72 Hz時，所對應的加速度響應分別約為0.35、0.50、0.60 g；樹枝部分的2階共振頻率約為1.74 Hz時，所對應的加速度響應分別約為0.55、080、1.00 g，即隨著激振載荷數值的增加，樹干、樹枝各自的加速度響應幅值是逐漸增加的。[FL）]

[FK（W+112mm][TPWTP2.tif][FK）]

2材料與方法

2.1試驗儀器

激振器：采用蘇州蘇試試驗儀器股份有限公司生產的電動振動試驗臺，振動試驗臺型號為DC-600-6，支持最大負載200 kg，額定位移 51 mm。信號采集：采用東華測試生產的采集儀及其配套的軟件，采集儀型號為DH5922N，可同時進行16通道同步高速長時間連續采樣，每個通道最高采樣頻率為256 kHz，本次試驗采樣頻率為500 Hz。

2.2試驗過程

提取1、2、3、4、5、6這6個監測點作為試驗的監測點，將加速度傳感器按編號1～6分別安置在6個監測點處，在點1處，分別依次施加5、7、9 g的激振載荷，應用采集儀同時對6個監測點進行監控并拾取響應。

2.3試驗結果

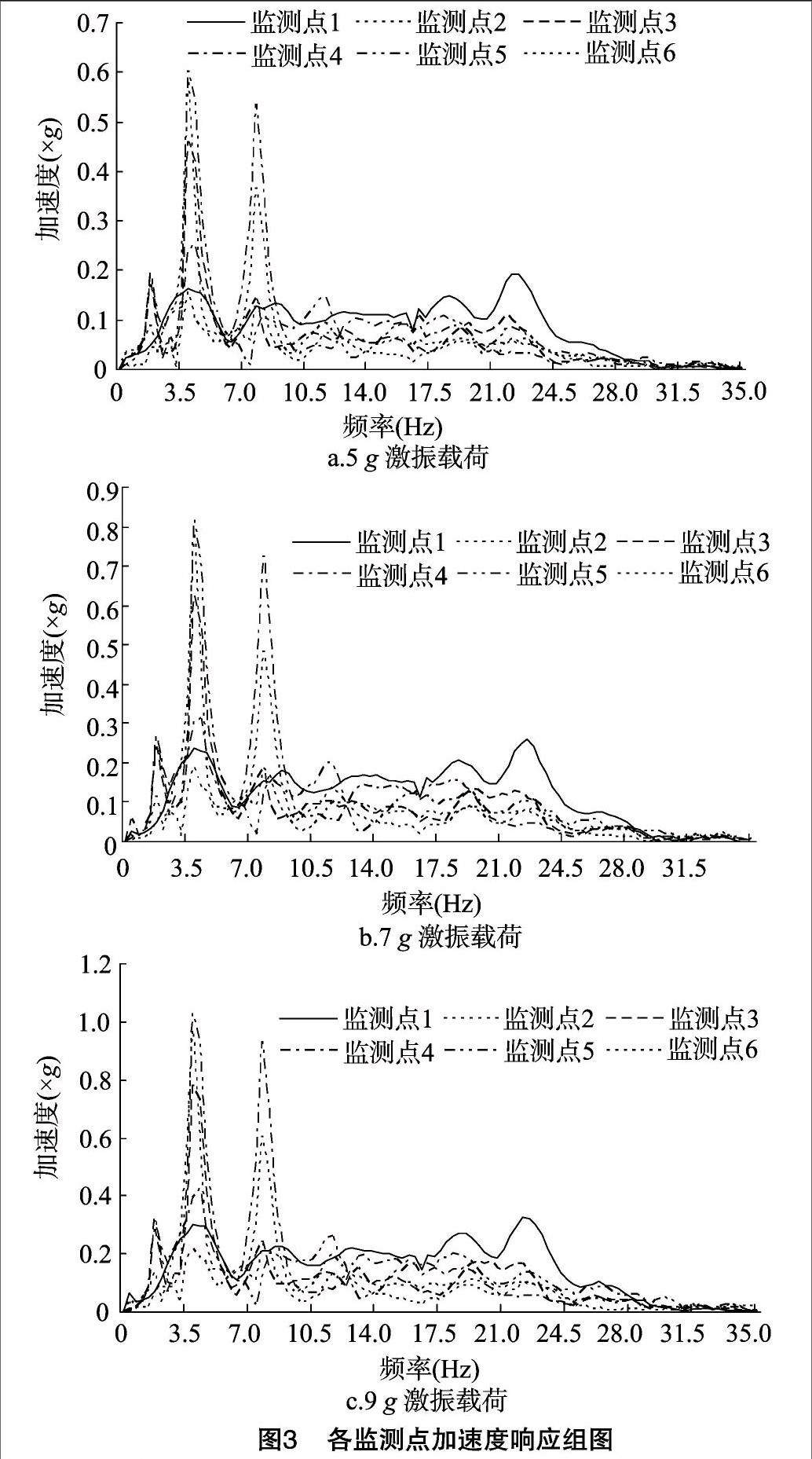
圖3-a、圖3-b、圖3-c分別表示的是系統在5、7、9 g激振載荷作用下的樹干、樹枝上各監測點的加速度響應圖。

通過對比圖3-a、圖3-b、圖3-c發現，在不同的激振載荷作用下，樹干、樹枝上各監測點的加速度響應圖也非常相似，這與前面仿真運算的結果可能存在一定的共性，因此，將仿真與試驗中的各階共振頻率一并列在表2中，將仿真與試驗所得的結果進行對比分析。

首先，從圖3-a、圖3-b、圖3-c中可以看出，試驗中整個果樹約共出現了6階共振頻率，其中2階、3階最為明顯，分別約為3.94、7.72 Hz。這與仿真中，樹干、樹枝部分分別共出現了6階、7階共振頻率，樹干中2階、3階、4階最為明顯，依次分別為4.18、7.71、18.87 Hz，樹枝中1階、2階、3階最為明顯，依次分別為1.13、1.74、4.18 Hz所得的結果，無論是共振頻率的階數，還是共振頻率的數值都較吻合。共振頻率對應的加速度響應越強烈，越有利于振動過程中果實的脫落，因此，上述的幾個共振頻率，可以作為整個果樹振動落果的首選參考頻率。

由表2可知，共振頻率在不同的激振載荷下，樹干、樹枝上各監測點的各階共振頻率始終都是在0～12、18～23 Hz這2個頻率區間，且在各區間內，各階共振頻率也幾乎一一對應。這與仿真中，樹干、樹枝的各階共振頻率始終都是在0～10、17～25 Hz這2個頻率區間內，且在各區間內，樹干、樹枝各階共振頻率也幾乎一一對應所得的結果，無論是頻率區間，還是共振頻率的對應關系都較吻合。說明激振載荷數值的增加，并不會改變果樹共振頻率的階數、區間、數值，同時0～12、17～25 Hz這2個頻率區間，可以作為整個果樹振動落果的參考頻率區間。

試驗中整個果樹在5、7、9 g的激振載荷作用下，樹干上監測點4的3階共振頻率約為7.68 Hz時所對應的加速度響應分別約為0.55、0.70、0.95 g，樹枝上監測點5的2階共振頻[CM（25]率約為3.94[KG*3]Hz時所對應的加速度響應分別約為0.60、080、1.00 g。這與仿真中，隨著激振載荷數值的增加，樹干、樹枝各自的加速度響應幅值是逐漸增加的相吻合。當果樹振動時的慣性力大于果實-果柄的結合力時，果實脫落，而慣性力主要取決于枝干上的加速度響應，因此，振動落果作業中，應綜合考慮樹干、各樹枝上果實的生長情況，選擇最適宜的激振載荷，以達到最大采摘效率。

仿真和試驗所得的結果中，諸如共振頻率的階數、數值、區間以及共振頻率所對應的加速度響應幅值，都存在微小的差異，這主要由于建立的模型不是很精確，比如忽略樹干、樹枝末端少量的嫩枝、嫩葉的重力，忽略空氣阻尼在仿真中的影

[FL）]

[KH*4D]

響，以及果樹分叉節點、枝干各處的材料形狀不一、物理特性不均勻等，都造成了理論模型的不精確性，從而造成了仿真與實際試驗的諸多差異。

3結論

[JP2]果樹振動落果過程中，0～12、17～25 Hz這2個頻率區間，可以作為整個果樹振動落果的參考頻率區間。其中，1.72、418、7.72 Hz可以作為整個果樹振動落果的首選參考頻率。

激振載荷數值的增加，果樹共振頻率的階數、區間、數值并不會隨之改變，但樹干、樹枝的加速度響應幅值是逐漸增加的。[JP]

樹干、樹枝末端少量的嫩枝、嫩葉的重力、空氣阻尼以及枝干材料物理特性不均勻等因素，對理論模型精度均有一定的影響，不容忽略。

參考文獻：

[1]Sarig Y. Mechanized fruit harvesting：Site specific solutions. Information and technology for sustainable fruit and vegetable production FRUTIC 05[C]. Montpellier，France，2005：237-247.

[2]王長勤，許林云，周宏平. 偏心式林果振動采收機的研制與試驗[J]. 農業工程學報，2012，28（16）：10-16.

[3]Torregrosa A，Martin B，Ortiz C，et al. Mechanical harvesting of processed apricots[J]. Applied Engineering in Agriculture，2006，22（4）：499-506.[HJ1.7mm]

[4]陳度，杜小強，王書茂. 振動式果品收獲技術機理分析及研究進展[J]. 農業工程學報，2011，27（8）：195-200.

[5]王業成，陳海濤，林青. 黑加侖采收裝置參數的優化[J]. 農業工程學報，2009，25（3）：79-83.

[6]Láng Z. A fruit tree stability model for static and dynamic loading[J]. Biosystems Engineering，2003，85 （4）：461-466.

[7]Láng Z. A simple model for fruit tree shaking harvest[J]. [JP2]International Journal of Horticultural Science，2007，13（1）：33-36.[JP]

[8]Láng Z. A one degree of freedom damped fruit tree model[J]. Transactions of the ASABE，2008，51（3）：823-829.

[9]李惠斌. 振動理論與工程應用[M]. 北京：北京理工大學出版社，2006：28-45.

[10]殷祥超. 振動理論與測試技術[M]. 徐州：中國礦業大學出版社，2007：30-43.

[11]李德葆. 工程振動試驗分析[M]. 北京：清華大學出版社，2004：23-39.

[12]黎明安. MATLAB/Simulink動力學系統建模與仿真[M]. 北京：國防工業出版社，2012：27-36.