變截面加筋板尺寸-布局一體化設計

王 博，田 闊，郝 鵬，鄭巖冰，趙海心，王捷冰

(1.大連理工大學 工程力學系 工業裝備結構分析國家重點實驗室，大連 116024；2.空間物理重點實驗室，北京 100076)

變截面加筋板尺寸-布局一體化設計

王 博1，田 闊1，郝 鵬1，鄭巖冰1，趙海心1，王捷冰2

(1.大連理工大學 工程力學系 工業裝備結構分析國家重點實驗室，大連 116024；2.空間物理重點實驗室，北京 100076)

為了提高加筋板結構的開口補強效率，文中提出了一種新型變截面加筋構型。通過豐富加筋結構層級，有效抑制了開口引發的失穩變形擴展，從而提高了結構的承載能力。在優化設計中，為了合理縮減設計變量的數目，文章采用函數變量來分別描述加筋層級與布局的變化規律。進而基于代理模型，實現了尺寸-布局一體化設計。最后，與等尺寸、等布局優化方法及等布局、尺寸余弦分布的優化方法的結果進行對比，凸顯了文中所提出的一體化設計方法的簡潔與有效。

多級加筋板；開口補強；極限承載力；一體化設計

0 引言

為滿足設備安裝、管線鋪設、散熱等功能型需求，開口不可避免地出現在火箭儀器艙、導彈級間段和飛機機身等航空航天加筋結構中[1-2]。開口引起了加筋板的局部剛度折減，導致開口處過早發生局部失穩，進而擴展至結構整體失效[3]。為了有效提高開口加筋板的承載能力，亟需提出新穎而高效的開口補強方法。Shi等[4]面向軸壓復合材料加筋柱殼結構，從抵抗開口附近失穩的角度提出了多種局部加筋補強構型。Dang等[5]、Hao等[3,6]在開口加筋平板、曲板及圓柱殼中，采用曲線加筋替代直筋，自適應地增大了補強的優化空間。

近年來，受到巨型土木建筑[7]及生物力學[8]中蘊含的層級理念的啟發，學者們提出了具備高承載能力的多級加筋結構形式[9-11]。傳統的單一層級的加筋結構具有一致的筋條形貌，而多級加筋結構在不同層級間具有明顯的幾何或材料差異，形成變截面特征。由于結構層級的豐富，多級加筋結構對局部幾何缺陷[12]、裂紋擴展[13]等所引起的局部剛度衰減表現出優異的容忍性，有利于保持較高的結構承載力。盡管層級增多帶來的增益很大，但現有的多級加筋結構的研究工作中筋條大多不超過2個層級[9-14]，這是因為隨著結構層級的增多，設計變量的數目也將激增，給優化設計帶來巨大困難[15]。為了有效表征此類多層級加筋結構的變截面信息，Khvyiuzov等[16]和Quinn等[17]分別采用正弦和余弦函數來描述不同層級間的筋條高度分布。

為了提高加筋板優化設計的效率，馮玉龍等[18]提出了并行子空間法來對復合材料加筋板進行布局與尺寸優化。榮曉敏等[19]基于進化神經網絡方法建立了復合材料格柵加筋板的代理模型，有效提高了結構優化效率。Wang等[20]針對非均勻軸壓工況下的網格加筋殼，提出了加筋布局函數，合理減少了布局優化的變量數目。在此基礎上，Hao等[3,6]建立了曲線加筋的布局函數。

本文首先針對軸壓工況下的加筋板結構，研究了開口對結構承載能力的折減效應及對失穩模式的影響；進而提出了簡潔的變量函數來分別描述變截面加筋層級與布局的變化規律，建立了基于代理模型的優化框架，并開展了以最大化結構承載力為目標的尺寸-布局一體化設計；最后與傳統的等尺寸-布局、等布局、尺寸余弦分布的補強方法的優化結果進行對比。

1 開口加筋板承載能力分析

1.1 開口加筋板模型

本文以文獻[9]中的典型加筋板作為算例，研究開口對加筋板承載能力的折減效應及失穩模式的改變。加筋板結構示意圖如圖1(a)和(b)所示。加筋板蒙皮長度Lm=480 mm，寬度bm=360 mm，厚度tm=2 mm。共有9根加筋條，其高度hr=12 mm，厚度tr=4 mm，筋條間的間距br1=40 mm，蒙皮側邊與鄰近的筋條距離br2=20 mm。模型材料屬性：彈性模量E=72 000 MPa，泊松比為ν=0.31，密度ρ=2.8×10-6kg/mm3，屈服強度363 MPa，強度極限為463 MPa，延伸率為12%。本文在此完美加筋板模型的中部增加一個長圓形開口，這種開口形式在航空航天、船舶工程中普遍存在[21-22]，相應的開口尺寸參數如圖1(c)和(d)所示，其中Lc=80 mm，Rc=60 mm。

1.2 開口加筋板承載能力分析

與文獻[9]一致，本文基于有限元軟件ABAQUS顯式動力學方法的準靜態求解技術來準確地模擬結構后屈曲行為，進而得到結構極限承載力。基于四節點殼體減縮積分單元S4R對加筋板模型進行離散，其對于薄殼和厚殼均具有很好的適用性[23]。通過網格收斂性分析確定模型的單元尺寸為5 mm，且筋條高度方向劃分兩層單元。模型邊界條件及加載條件如下：側邊自由，底端固支，頂端約束除軸向位移外的其余自由度，并將頂端面所有節點剛性耦合至參考點，在參考點上施加軸壓位移載荷直至結構發生失穩破壞。對模型加載時間進行收斂性分析，確定顯式動力學分析的加載時間為200 ms，加載總位移為2 mm。圖2為計算得出的完美加筋板與開口加筋板位移-載荷曲線及其變形云圖，其中完美加筋板與含開口加筋板極限承載力分別為165.9 kN和 123.4 kN。由于開口的存在，結構承載力降低了 25.6%。可看出，完美加筋板失穩波形主要集中在結構中部，并隨著位移的不斷加載而擴展至結構整體；而含開口加筋板失穩波形率先發生在開口周圍的蒙皮處，使得局部區域更容易發生屈曲變形，導致結構剛度迅速折減，過早地發生整體失效。

2 開口加筋板尺寸-布局一體化設計框架

2.1 加筋板尺寸-布局函數

針對開口所引起的加筋板剛度折減，羅楚養等[21]指出合理的加筋優化是一種有效的補強方法。需要指出的是，為保證結構關于X軸的對稱性，第0號筋條位置被固定，且左右兩側筋條的尺寸和布局均關于X軸對稱。本文定義單側筋條數目為n個，則加筋板筋條總數N=2n+1，為后文表述的清晰，本文以單側筋條數目n作為設計變量，相應的筋條標號如圖1所示。同時，為了防止側邊屈曲的發生，在優化中須固定靠近邊界處的第n號筋條的位置。由此可見，本文以圖1(b)所示的Ld區域作為設計區域(Ld=bm/2-br2)，可優化設計的變量為第0～n號筋條的高度、第1～(n-1)號筋條的布局、筋條的厚度(所有筋條具有統一厚度)。

若所有的尺寸-布局變量都是獨立的，則總計有(2n+1)個設計變量。當單側筋條數目n增多時，上述設計變量數目也將激增，這極大地制約了優化效率。若采用等尺寸-布局設計，則變量數目降至3個，僅包括單側筋條數目n、筋條統一高度hr和厚度tr。雖然減少了設計變量數目，但這樣的設計人為地縮小了設計空間，很難自適應地補強開口所引起的局部剛度折減，易導致較低的補強效率。為了減少用來表征變截面加筋尺寸的變量數目，Quinn[17]等采用余弦函數來描述不同層級間的筋條高度分布，如式(1)所示。其中，Li代表第i號筋條距離第0號筋條(對稱中心)的間距，hi代表第i號筋條的筋高，hα和hβ分布代表第0號和第n號筋條的筋高。由圖3可看出，當hα=hβ時，筋條等高度；當hαhβ時，筋條高度關于對稱中心X軸遞增。這種等布局、尺寸余弦分布的方法中包含了單側筋條數目n、筋條高度hα和hβ、厚度tr共4個設計變量。

(1)

為了更有效地實現尺寸與布局的一體化設計，本文以2個變量函數λ1和λ2來分別表征布局和尺寸變量，以期合理減少設計變量的數目。第i號筋條的間距Li和筋高hi的表達式如式(2)所示。變截面加筋板的所有布局-尺寸變量可由布局和尺寸變量λ1和λ2、單側筋條數目n、筋條厚度tr和第n號筋條的筋高hn這5個變量表示，表述簡捷清晰。

i=0,1,…,n

(2)

圖4更直觀地表現了變量函數λ1和λ2的效果。當λ1= 1時，筋條等間距布局；當λ1< 1時，筋條關于對稱中心X軸分布稀疏而在兩端分布密集；當λ1> 1時，筋條關于對稱中心X軸分布密集而在兩端分布稀疏；當λ2= 1時，筋條等高度；當λ2< 1時，筋條高度關于對稱中心X軸遞減；當λ2> 1時，筋條高度關于對稱中心X軸遞增。

2.2 徑向基函數(RBF)代理模型

加筋板的后屈曲分析過程非線性程度較高且分析耗時較大，RBF模型被認為是處理此類問題非常有效、可靠的方法。RBF模型是一類以待測點與樣本點間的歐氏距離為自變量的函數為基函數，進而通過線性加權的方式構造出來的代理模型，可把一個多維問題轉化成為以歐氏距離為自變量的一維問題，其基本表達形式如下[24]：

φ(r)

(3)

r=‖x-xj‖

(4)

式中R(x)為預測值；λj為權系數；x為設計變量矢量；xj為第j個樣本點上的設計變量矢量；r為第j個樣本點與待測點間的歐氏距離；φ為基函數；n為樣本點數量，其網絡結構圖如圖5所示。

基于此模型，可建立起加筋板結構尺寸參數等輸入量與結構承載力及質量等輸出量之間的近似擬合關系，后續的優化設計可基于此代理模型開展。

2.3 開口加筋板尺寸-布局一體化設計框架

依據上述變量函數，本文提出了基于代理模型的開口加筋板尺寸-布局一體化設計框架，如圖6所示。其框架流程如下：

(1)根據變量函數λ1和λ2，建立變截面加筋板有限元模型。

(2)基于最優拉丁超立方法[25]在設計空間抽取樣本點，建立徑向基函數(RBF)代理模型后，再另外抽取樣本點進行誤差評估，得到均方根誤差(Root Mean Square Error，RMSE)、平均百分誤差(Percent Average Error, AvgErr)、最大百分誤差(Percent Maximum Error, MaxErr)3個誤差表征結果[3]。其值越小，表示代理模型的擬合精度越高[26]。如果誤差指標在可接受范圍內，則接受所創建的代理模型，否則重新構建[27]。

(3)基于代理模型進行內層優化，選取多島遺傳方法作為優化算法。

(4)內層優化收斂后，調用一次精細模型分析來驗證代理模型最優解的準確性。如果預測誤差在0.5%以內則優化結束；如果精度不滿足則將最優解的精細模型結果添加到初始代理模型中，生成新的代理模型，實施外層更新，再進行第三步，循環迭代，直至外層更新精度收斂，優化結束。

3 開口加筋板優化算例

基于本文提出的一體化設計框架開展優化設計，以λ1、λ2、n、tr和hn作為設計變量，以結構質量W不超過初始質量1.36 kg作為約束條件，以最大化結構極限承載力Pco作為優化目標，相應的優化空間如表1所示。同時，本文以等尺寸-布局優化[28]和等布局、尺寸余弦分布的優化[17]作為對比算例。等尺寸-布局優化的設計變量中單側筋條數目n和筋條厚度tr的取值范圍與一體化設計保持一致。筋條高度變量hr的上下限范圍可根據一體化設計中hn、n、λ1和λ2的上下限取值來確定，如式(5)所示。這樣的設置確保了2種優化方案的可對比性，等尺寸-布局優化空間如表2所示。等布局、尺寸余弦分布的優化中4個設計變量n、hα、hβ和tr的取值范圍均與等尺寸-布局優化保持一致，其優化空間如表3所示。為了表述方便，分別命名上述尺寸-布局一體化設計、等尺寸-布局優化和等布局、尺寸余弦分布優化為優化1、優化2和優化3。

(5)

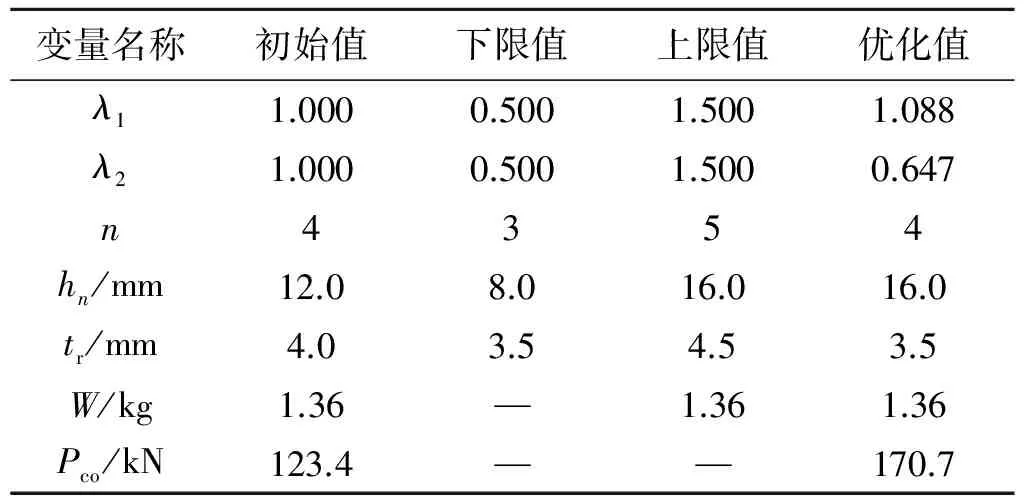
表1 優化1中優化變量的取值范圍與優化值

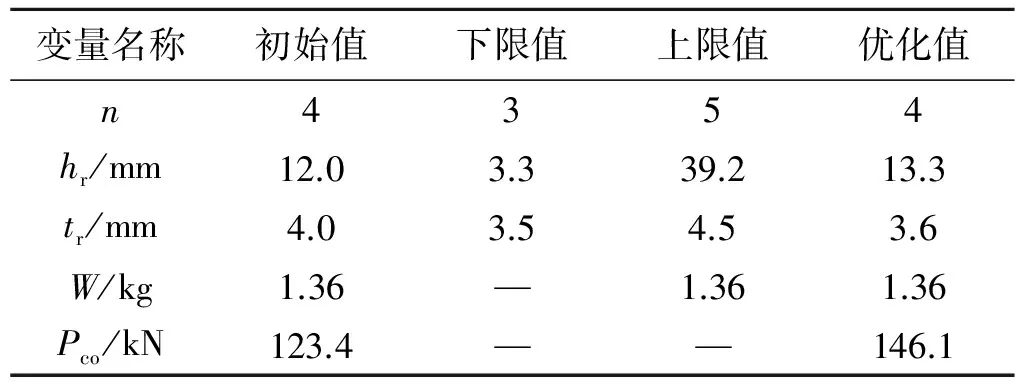
表2 優化2中優化變量的取值范圍與優化值

針對以上3個算例，分別基于最優拉丁超立方方法抽取150個樣本點后建立代理模型，再抽取另外的12個樣本點來校驗其誤差指標，結果如表4所示，3個算例代理模型的預測精度均滿足需求，可用于開展后續的優化設計。如圖7所示，歷經4次外層更新來不斷修正代理模型的精度，優化過程收斂。在保持結構質量不變的情況下，一體化設計優化解的極限承載力(170.7 kN)相較于初始值(123.4 kN)提高了38.3%，且比等尺寸-布局優化解(146.1 kN)提高了16.8%，比等布局、尺寸余弦分布的優化解(144.9 kN)提高了17.8%，這凸顯了一體化設計方法在開口補強設計中的巨大優勢。需要指出的是，一體化設計優化解(170.7 kN)甚至高于沒有開口時完美加筋板的承載力(165.9 kN)，進一步表明了新方法的有效性。

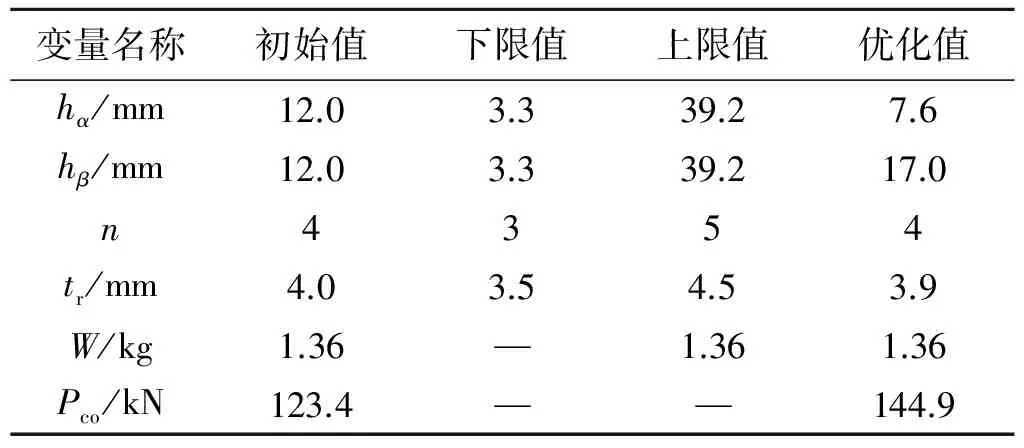
表3 優化3中優化變量的取值范圍與優化值

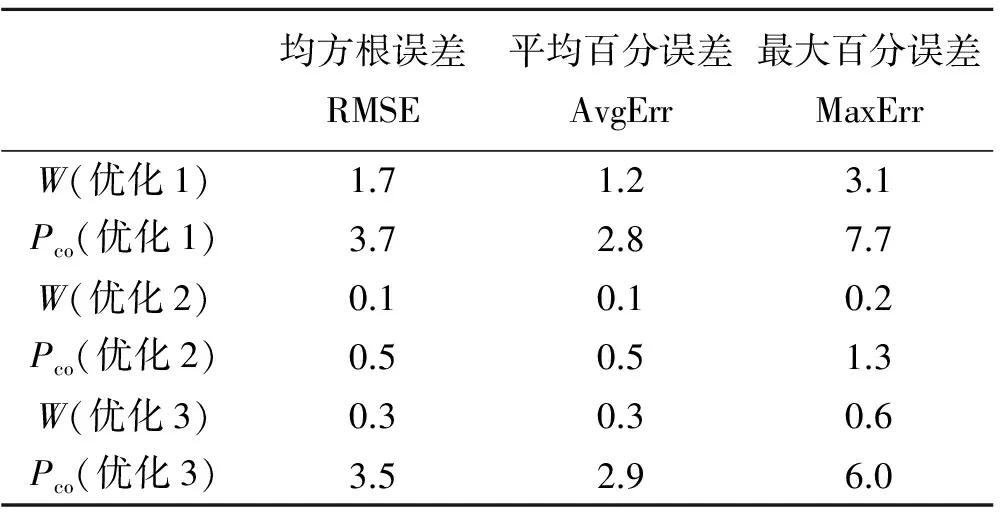
表4 3個優化算例中代理模型誤差指標

圖8～圖10分別給出了初始設計、優化1、優化2和優化3的幾何構型、位移-載荷曲線和變形云圖的對比圖。

3個優化算例的優化解與初始設計相比，筋條數目均未發生變化，表明了提高承載力這一目標對筋條數目這一變量并不敏感。優化2為等尺寸-布局優化，其優化解在減小筋條厚度的基礎上將筋條高度增加至13.3 mm，有效提高了筋條的抗彎剛度，抑制了局部屈曲變形由開口區向結構整體的擴展，進而提高了結構承載力。相較于優化2，優化1具有更靈活的設計空間，如圖8(a)所示，其優化后筋條關于對稱中心X軸分布更為緊密，自適應地補強了開口周圍的剛度，有利于抑制局部屈曲的過早發生。優化1的筋條高度關于對稱中心X軸遞減，在開口區域內的筋條高度較低(h0=9.0 mm，h1=11.5 mm)，均小于優化2的筋條高度(hr=13.3 mm)，表明在開口區域內進行加筋補強的效果并不明顯；優化1在近開口區域的筋條高度(h2=13.3 mm)與優化2的筋條高度(hr=13.3 mm)相同，但在位置上更靠近開口區域，有利于抵抗局部屈曲的過早發生，補強優勢更明顯；優化1在遠開口區域的筋條高度(h3=14.7 mm，h4=16.0 mm)均大于優化2的筋條高度，且更靠近開口區域，使筋條具有更大的抗彎剛度，提高了遠開口區域筋條抵抗局部屈曲變形擴展的后屈曲承載能力。盡管優化3的優化解中筋條高度變化趨勢與優化1的結果較為相似，均表現為向對稱中心遞減，但需要指出的是，由于優化3僅能改變筋條高度余弦分布函數的幅值，無法自適應地調整布局，因而相較于優化1的設計空間受到限制，未能優化到更優異的結果。綜上所述，優化1的優化解相較于初始設計、優化2和優化3的優化解，通過自適應提高近開口區和遠開口區筋條的抗彎剛度，對局部屈曲變形發生、后屈曲變形擴展均具有很好的抵抗作用，體現了變截面加筋設計理念在解決開口剛度折減問題上的巨大優勢。

4 結論

本文從豐富結構層級的角度提出了一種新型多級加筋板結構形式，并基于代理模型技術建立了尺寸-布局一體化設計框架，通過算例對比得出如下結論：

(1)本文提出的變量函數合理縮減了設計變量的數目，有效表征了變截面多級加筋的尺寸和布局信息。

(2)通過優化算例對比，驗證了本文提出的尺寸-布局一體化設計方法的有效性，且相較于傳統的等尺寸-布局方法和等布局、尺寸余弦分布方法更易尋找到更優的設計結果。

(3)變截面筋條由于設計變量的靈活性，可自適應地在近開口區域抑制局部屈曲過早發生，并在遠開口區域抵抗后屈曲變形的擴展，在開口補強設計中比等截面筋條更具承載優勢。

[1] Behavior of compression-loaded quasi-isotropic curved panels with a circular cutout[J]. International Journal of Solids and Structures, 2001, 38(9): 1495-1522.

[2] 展全偉, 范學領, 孫秦. 復合材料孔板在濕熱環境下的力學性能研究[J]. 固體火箭技術, 2011, 34(6): 764-767.

[3] Hao P, Wang B, Tian K, et al. Optimization of curvilinearly stiffened panels with single cutout concerning the collapse load[J]. International Journal of Structural Stability and Dynamics, 2015: 1550036-1-1550036-21.

[4] Shi S S, Sun Z, Ren M F, et al. Buckling response of advanced grid stiffened carbon-fiber composite cylindrical shells with reinforced cutouts[J]. Composites Part B: Engineering, 2013, 44(1): 26-33.

[5] Dang T D, Kapania R K, Slemp W C H, et al. Optimization and postbuckling analysis of curvilinear-stiffened panels under multiple-load cases[J]. Journal of Aircraft, 2010, 47(5): 1656-1671.

[6] Hao P, Wang B, Tian K, et al. Efficient optimization of cylindrical stiffened shells with reinforced cutouts by curvilinear stiffeners [J]. AIAA Journal, 2015.

[7] Lakes R. Materials with structural hierarchy[J]. Nature, 1993, 361(6412): 511-515.

[8] Gao H, Ji B, J?ger I L, et al. Materials become insensitive to flaws at nanoscale: lessons from nature[J]. Proceedings of the National Academy of Sciences, 2003, 100(10): 5597-5600.

[9] 王博, 田闊, 郝鵬, 等. 多級加筋板結構承載性能與缺陷敏感度研究[J]. 固體火箭技術, 2014, 37(3): 408-412.

[10] 徐元銘, 李松澤. 整體次加筋壁板屈曲載荷近似計算方法[J]. 北京航空航天大學學報, 2015, 41(3): 369-374.

[11] 隋倩倩, 江舒, 孫方方, 等. 多級三角形格柵夾芯結構力學性能分析[J]. 復合材料學報, 2016,33(3):675-680.

[12] Wang B, Hao P, Li G, et al. Optimum design of hierarchical stiffened shells for low imperfection sensitivity[J]. Acta Mechanica Sinica, 2014, 30(3): 391-402.

[13] Quinn D, Murphy A, Cervi L. Fatigue performance of aircraft panels with novel skin buckling containment features[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2011, 225(7): 791-806.

[14] Houston G, Quinn D, Murphy A, Bron F. Wing panel design with novel skin-buckling containment features[J]. Journal of Aircraft, 2015: 1-11.

[15] Pappas M, Moradi J. Optimal design of ring stiffened cylindrical shells using multiple stiffener sizes[J]. AIAA Journal, 1980, 18(8): 1020-1022.

[16] Khvyiuzov A, Xu Y M. Initial buckling of compressed rectangular panels with variable stiffener sizes[J]. Advanced Materials Research, 2014, 915: 150-164.

[17] Quinn D, Murphy A, Glazebrook C. Aerospace stiffened panel initial sizing with novel skin sub-stiffening features[J]. International Journal of Structural Stability and Dynamics, 2012, 12(5): 1250060.

[18] 馮玉龍, 程家林, 姚衛星. 復合材料加筋板結構的并行空間協同優化設計方法[J]. 南京航空航天大學學報, 2013, 45(3): 360-366.

[19] 榮曉敏, 徐元銘, 吳德財. 進化神經網絡在復合材料格柵結構設計中的應用[J]. 固體火箭技術, 2006, 29(4): 305-309.

[20] Wang B, Hao P, Li G, et al. Two-stage size-layout optimization of axially compressed stiffened panels[J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 313-327.

[21] 羅楚養, 熊峻江, 益小蘇, 等. 復合材料蒙皮-加筋大開口結構優化設計[J]. 材料工程, 2011(4): 9-13.

[22] Kim J H, Jeon J H, Park J S, et al. Effect of reinforcement on buckling and ultimate strength of perforated plates[J]. International Journal of Mechanical Sciences, 2015, 92: 194-205.

[23] 莊茁. 基于ABAQUS的有限元分析和應用[M]. 北京:清華大學出版社, 2009.

[24] 郝鵬, 王博, 鄒威任,等. 基于RBF模型的蒙皮桁條結構減輕孔優化[J]. 固體火箭技術, 2015, 38(5): 717-721.

[25] 陳兵, 谷良賢, 龔春林. 適用于寬馬赫數的尾噴管優化設計[J]. 固體火箭技術, 2013, 36(6): 758-762.

[26] 郝鵬. 面向新一代運載火箭的網格加筋柱殼結構優化研究[D]. 大連: 大連理工大學, 2013.

[27] 趙良玉, 楊樹興, 佘浩平. 火箭彈氣動學科代理模型構建方法研究[J]. 固體火箭技術, 2007, 30(1): 1-4.

[28] 張柱國, 姚衛星, 劉克龍. 基于進化Kriging模型的金屬加筋板結構布局優化方法[J].南京航空航天大學學報, 2008, 40(4): 497-500.

(編輯：薛永利)

Size-layout integrated optimization of variable cross-section stiffened panels

WANG Bo1, TIAN Kuo1,HAO Peng1,ZHENG Yan-bing1, ZHAO Hai-xin1,WANG Jie-bing2

(1.State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics,Dalian University of Technology, Dalian 116024, China；2.Science and Technology on Space Physics Laboratory, Beijing 100076, China)

In order to improve the efficiency of cutout reinforcements, a novel variable cross-section stiffened panel was presented in this paper. Due to the hierarchical characteristic of stiffeners, the development of deformations caused by the cutout was restricted effectively, therefore the load-carrying capacity of the stiffened panel increases. Aiming at reducing the number of design variables in the optimization, distribution functions were used to describe both the size and layout variables of stiffeners. Based on the surrogate model, a size-layout integrated optimization framework was established. Finally, the simplicity and effectiveness of the novel optimization framework were validated by comparison with that using uniform size and layout variables and that using uniform layout variables and cosine-type distributed size variables.

hierarchical stiffened panels；cutout reinforcement；load-carrying capacity；integrated optimization

2015-10-09；

2016-01-26。

973項目(2014CB049000)；國家自然科學基金(11372062，11402049，91216201)；博士后特別資助基金(2015T80246)；高等學校學科創新引智計劃(B14013)；遼寧省高等學校優秀人才支持計劃(LJQ2013005)。

王博(1978—)，男，教授，主要從事結構與多學科優化、航天先進材料與結構設計和耐撞性優化設計研究。E-mail:wangbo@dlut.edu.cn

郝鵬(1986—)，男，博士，主要從事結構可靠性分析與優化研究。E-mail:haopeng@dlut.edu.cn

V414.3

A

1006-2793(2017)02-0208-06

10.7673/j.issn.1006-2793.2017.02.014