理知識脈絡抓重點難點看問題本質

姜鴻雁

理知識脈絡抓重點難點看問題本質

姜鴻雁

一、關注圖形變化前后的“對應”

無論哪類圖形變換，關注圖形變化前后的對應關系是關鍵，關注對應點、對應角、對應邊，則便于發現平移的距離、旋轉的角度、對稱軸或比例線段等關于圖形變換的重要“指標”，也便于運用各類圖形變換的性質，使問題迎刃而解.

例1（2016·新疆）如圖1，將一個含30°角的直角三角板ABC繞點A旋轉，使得點B、A、C′在同一條直線上，則三角板ABC旋轉的角度是（）.

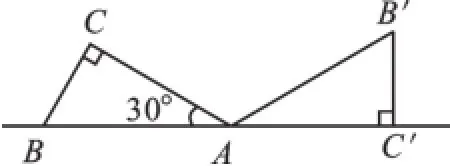
圖1

A.60°B.90°C.120°D.150°

【解析】C、C′是對應點，AC、AC′是對應邊，因為對應邊夾角是旋轉角，所以∠CAC′是旋轉角，所以本題選D.

例2（2016·泰州）如圖2，在△ABC中，BC=5cm，將△ABC沿BC方向平移至△A′B′C′的對應位置時，A′B′恰好經過AC的中點O，則△ABC平移的距離為cm.

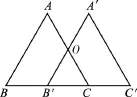
圖2

【解析】圖形平移的距離是指對應點之間的距離，即BB′或CC′的長，由平移的性質知對應邊平行，易得△OB′C∽△ABC，因為O為AC中點，所以相似比為，則B′C=2.5（cm），所以BB′=2.5（cm）.

二、關注圖形變化中整體與部分的關系

無論哪類圖形變換，部分與整體之間都存在著依存關系：圖形上每個點隨著圖形整體做相同方式運動.

例3（2016·青島）如圖3，線段AB經過平移得到線段A′B′，其中點A、B的對應點分別為A′、B′，這四個點都在格點上.若線段AB上有一個點P（a，b），則點P在A′B′上的對應點P′的坐標為（）.

A.（a-2，b+3）B.（a-2，b-3）C.（a+2，b+3）D.（a+2，b-3）

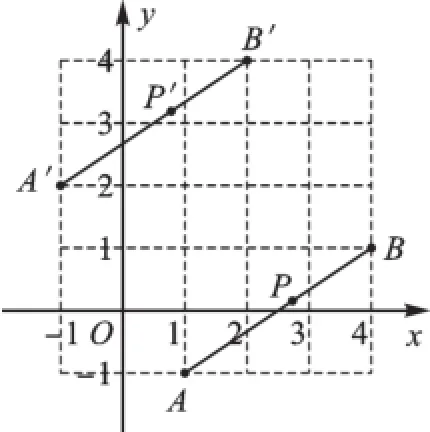
圖3

【解析】因為在運動過程中，圖形上所有的點都按相同的變化規律運動，雖然點P不是格點，但可以從線段端點A或B（它們是格點）容易發現變化規律是：向左平移2個單位，向上平移3個單位，所以答案為A.

三、關注坐標中“藏”著的“秘密”

當圖形放置在平面直角坐標系下，坐標可以確定圖形的位置，圖形的運動方式也可以通過坐標的方式來體現，善于發現坐標中的“秘密”，是我們發現問題本質的一條重要途徑.

例4（2016·濱州）正五邊ABCDE放入某平面直角坐標系后，若頂點A、B、C、D的坐標分別是（0，a）、（-3，2）、（b，m）、（c，m），則點E的坐標為（）.

A.（2，-3）B.（2，3）

C.（3，2）D.（3，-2）

【解析】正五邊形是軸對稱圖形，由A點坐標可知它在y軸上，C、D兩點的坐標“告訴”我們CD平行于x軸，所以本題的本質就是求B點關于y軸的對稱點E的坐標，故選C.

例5（2016·河南）如圖4，已知菱形OABC的頂點O（0，0），B（2，2），若菱形繞點O逆時針旋轉，每秒旋轉45°，則第60秒時，菱形的對角線交點D的坐標為（）.

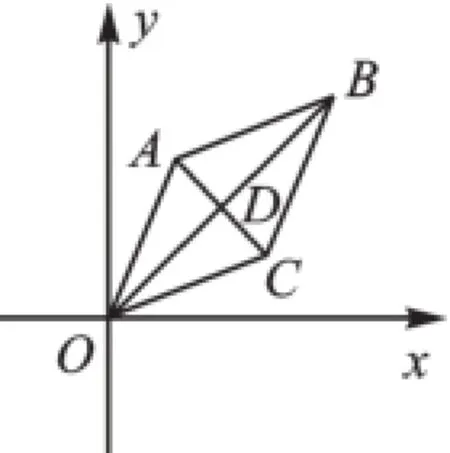
圖4

【解析】點B坐標（2，2）“藏”著OB與x軸夾角是45°，每秒旋轉45°，則意味著每8秒，點B回到原處，60秒時，點B旋轉到第三象限，而菱形繞O點旋轉時，點B、對角線交點D也同樣隨整體一起旋轉，所以此時點D的坐標是（-1，-1）.

四、圖形的變化是重要思想方法與策略

圖形的變化不僅是一個個具體的知識，也是我們解決問題的重要思想方法與策略，巧妙運用圖形變化思想，有助于我們發現問題的本質，繞開易錯的煩惱，達到事半功倍的效果.

例6（2016·淄博）如圖5是由邊長相同的小正方形組成的網格，A、B、P、Q四點均在正方形網格的格點上，線段AB、PQ相交于點M，則圖中∠QMB的正切值為.

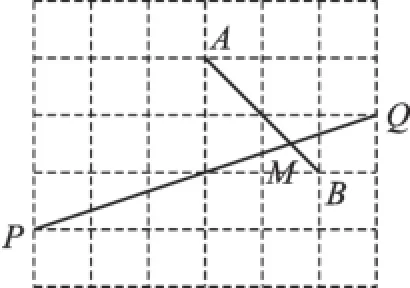
圖5

【解析】在網格問題中，應該關注格點，也“希望”要求的目標與格點相關，將線段AB上移一格再右移一格，使B、Q重合（如圖6），由平移性質得∠QMB=∠FQP，且△FQP是直角三角形，所以tan∠QMB=tan∠FQP=2.

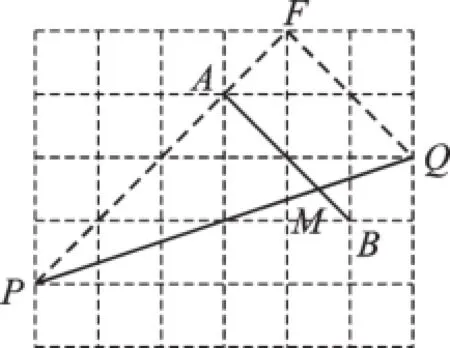
圖6

例7（2015·婁底）一塊三角板ABC按如圖7所示的方式放置，頂點A的坐標為（0，1），直角頂點C的坐標為（-3，0），∠B=30°，則B點的坐標為.

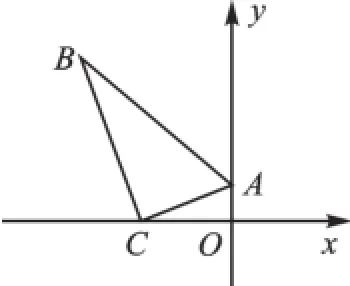
圖7

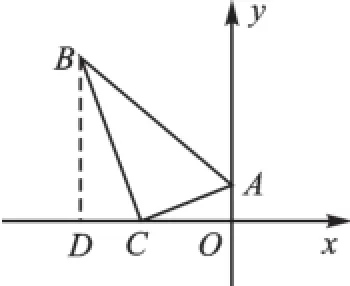
圖8

【解析】過B點作BD⊥x軸于D，由相似變換可知△OCA∽△DBC，又因為在Rt△ABC中，∠B=30°，所以兩個三角形的相似比為1∶，則DC=，DB=3.在求B點坐標時，我們可以這樣思考：B點是由C點向左平移再向上平移33個單位得到的，則B點的坐標為（-3-3，33）.用動態的思想求點的坐標，可以免去線段的長與坐標符號的正負性導致的錯誤.

結束語：圖形的變化既體現在位置關系的變化上也體現在數量關系的變化上，可以單一變化，也可以組合變化，可以從知識認識它們，更要從解決問題的方法和策略上去認識它們，它們在呼喚我們要善于用動態的眼光去看待一個靜態的圖形，用這種獨特的方式可以提升我們的思維能力.

（作者單位：江蘇省無錫市河埒中學）