[C2m im][Ala]丙氨酸離子液體水溶液粘滯流動的活化參數

佟靜 劉璐 張朵 鄭煦 陳霞 楊家振

(遼寧大學化學院，沈陽110036)

[C2m im][Ala]丙氨酸離子液體水溶液粘滯流動的活化參數

佟靜*劉璐 張朵 鄭煦 陳霞 楊家振

(遼寧大學化學院，沈陽110036)

在288.15－328.15 K溫度范圍內，測量了不同濃度的氨基酸離子液體[C2m im][Ala]水溶液的密度和粘度，根據Jones-Do le方程得到了較大正值的粘度B系數并且d B/d T＜0。借助Feakins理論，計算了溶質對溶液粘滯流動活化自由能貢獻Δμ2≠0，根據Δμ2≠0隨溫度的線性變化，進而得到流動活化熵ΔS2≠0和活化焓ΔH2≠0；在Eyring液體粘度的過渡態理論基礎上，提出了預測離子液體[C2m im][Ala]水溶液粘度的半經驗新方法，其預測值與相應的實驗值很好的一致。

離子液體；溶液粘度；粘度B系數；粘滯流動活化參數；過渡態理論

1 引言

眾所周知，離子液體是新型功能材料和對環境友好的綠色溶劑，由于其優良的物理和化學特性，近年來發展成為多學科交叉的熱門研究領域。目前已應用于有機合成、催化反應等與化學相關的各個領域1－3。然而，離子液體粘度普遍偏高是阻礙其應用的重要方面，因此，如何降低其粘度就成為離子液體研究領域的一個重要問題4,5。研究發現，如果粘滯的離子液體與少量的其它溶劑混合，就會極大地降低離子液體的粘度，其中溶液就是降低離子液體粘度的有效方法6,7。

另外，氨基酸離子液體(AAILs)是一類新的功能離子液體。由于氨基酸廣泛存在于自然界的生物體中，也把這類離子液體稱作自然離子液體(natural ILs)或生物離子液體(bio-ILs)，可以預見它們在生命科學研究、醫藥學研究中將會得到廣泛應用。然而，對離子液體水溶液粘度性質的研究較少，但在實際應用過程中，氨基酸離子液體溶液的基礎物理化學知識又是不可或缺的。粘度數據不僅為理論研究提供依據，也是相關工業開發應用的重要基礎。但是現存的粘度數據存在一些缺點：種類不全面，缺乏粘度數據的其他相關信息7－12。因此，作為我們前期研究工作的繼續12－16，本文研究了288.15－328.15 K溫度范圍內不同濃度[C2m im][Ala]水溶液的密度和粘度，應用Jones-Dole方程確定了不同溫度下的溶液粘滯流動B系數17－19，進而在Eyring過渡態理論基礎上提出了一個估算離子液體溶液粘度的半經驗新方法。

2 實驗部分

2.1 試劑與儀器

自制的去離子水13。實驗藥品的來源和純度詳見表1。用電子天平(METTLER TOLEDO AL104，瑞士)稱重，最大誤差為0.2mg。用奧地利Anton Paar公司生產的DMA 4500型振動管數字密度計測量這些樣品的密度，儀器最大誤差為0.00005 g· cm－3。用杭州中旺科技有限公司生產的Z-Clock 200粘度計測量這些樣品的粘度。

2.2 離子液體的合成

本實驗采用酸堿中和方法，經過兩步合成出[C2m im][A la]丙氨酸離子液體(見圖1)，此方法離子液體的產量高，且容易分離，具體步驟有關文獻已作詳細敘述12－14。所得產品通過核磁共振氫譜(1H NMR)進行了表征，并進行了元素分析測試，樣品純度≥0.99。用Karl Fischer法(上海市安亭電子儀器廠ZSD-2 13 type自動水份滴定儀)測定樣品的含水量，其質量分數w=3860×10－6。用AgNO3-HNO3溶液進行檢測，沒有發現鹵素離子。

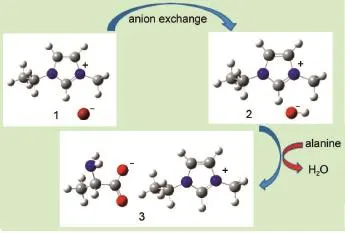
圖1 用中和法合成離子液體[C2m im][Ala]示意圖Fig.1 Schem e of p reparation of ionic liquids[C2m im][A la] by theneutralizationmethod1:[C2mim]Br;2:[C2mim][OH];3:[C2mim][Ala]

2.3 密度和粘度的測定

在質量摩爾濃度0.01－1.10mol·kg－1范圍內，用重量法配制一系列離子液體[C2m im][A la]水溶液樣品，并作空氣浮力校正。

在288.15－328.15 K溫度范圍內，測量樣品密度。密度計用標準方法標定，然后測定不同溫度下純水密度，與文獻值相比較20，測量誤差在±0.00002 g·cm－3之內。儀器本身的控溫精度為±0.01K。

在288.15－328.15 K溫度范圍內測量樣品的粘度。首先用多次經亞沸提純器處理的二次蒸餾水測定該儀器系數k，用帶有二級控溫裝置的恒溫水浴控制測量溫度，控溫精度為±0.02K。

3 結果和討論

3.1 [C2m im][A la]離子液體水溶液的平均摩爾體積和表觀摩爾體積

將在288.15－328.15 K范圍內測得的不同濃度樣品的密度值列入表2中，表中的每一個值都是三次測量的平均值。

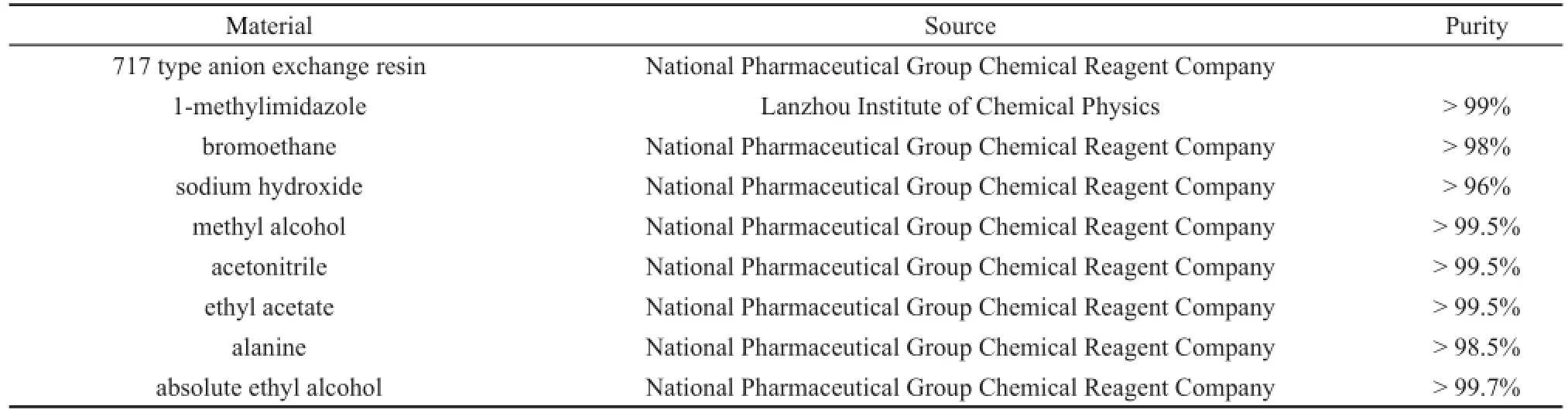
表1 實驗試劑來源和純度Table1 Sourceand purity of thematerials

利用表2中的離子液體溶液密度值，計算溶液的平均摩爾體積Vm：

其中Mm為溶液的平均摩爾質量。

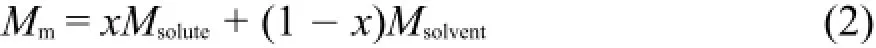
其中x為溶質的摩爾分數，其值從質量摩爾濃度換算得到21。將用方程(1)計算得到的溶液的摩爾體積Vm值列入表S1(Supporting Information)中。

利用方程(3)可從密度數據得到[C2m im][A la]離子液體水溶液的表觀摩爾體積φVB22：

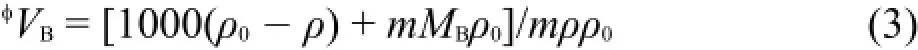
其中ρ0是水的密度；MB=199.25 g·mol－1，是溶質[C2m im][A la]離子液體的摩爾質量；ρ是離子液體水溶液的密度；m是離子液體水溶液的質量摩爾濃度。在指定溫度下，表觀摩爾體積與濃度的關系可用下面經驗方程表示：

其中a0和a1為經驗參數，a0等于無限稀釋表觀摩爾體積φVB0，不同溫度的φVB值列入表S2(Supporting Information)中。

3.2 離子液體[C2m im][A la]水溶液的粘度和B系數

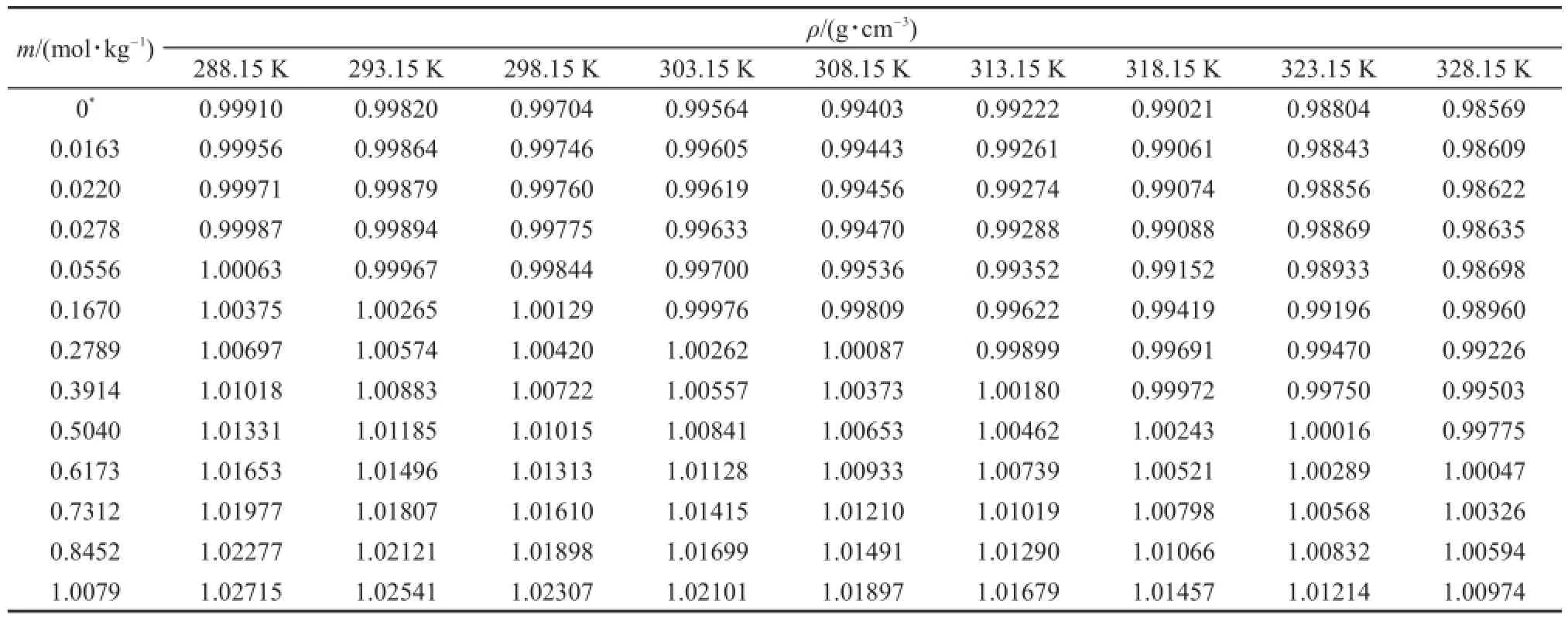
表2 288.15－328.15K不同濃度[C2m im][A la]溶液的密度測定值(ρ)Tab le2 Valuesof density(ρ)for aqueous[C2m im][A la]w ith variousmolalitiesat288.15－328.15K

表3 288.15－328.15K不同濃度[C2m im][A la]溶液的動力粘度值(η) Tab le 3 Valuesof viscosity(η)for aqueous[C2m im][A la]w ith variousm olalitiesat 288.15－328.15 K

表3列入了測得的不同溫度和濃度下的[C2m im][A la]離子液體水溶液的粘度，表中的每個數據都是三次測量的平均值。

強電解質水溶液的粘度可以用Jones-Dole經驗方程(5)描述17－21：

式中η和η0分別為溶液和溶劑的粘度，c為物質的量濃度，單位為mol·L－1(見表S3(Supporting Information))，其值可用測定的溶液密度數據換算21，A為表示長程靜電力的參數，B為溶液粘滯流動的粘度B系數。將方程(5)重排可得到確定粘度B系數的工作方程:

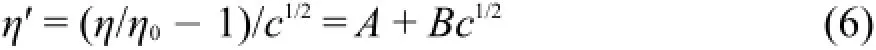
式中η′是外推函數，列入表S4(Supporting Information)中。將外推函數η′對c1/2作圖，可得到一組很好的直線，直線的斜率就是粘度B系數。圖2為293.15、303.15、313.15和323.15 K下η′對c1/2作圖的直線，288.15、298.15、308.15、318.15和328.15 K下η′對c1/2作圖的直線見圖S1(Supporting Information)。按方程(6)作線性擬合，將得到粘度B系數、參數A的值及其相關系數的平方r2和標準偏差s一并列入表4中。

圖2 293.15、303.15、313.15、323.15 K下外推函數η′對c1/2作圖Fig.2 Plotting extrapolation function ofη′vs c1/2at 293.15,303.15,313.15,323.15K■293.15K;●303.15 K;▲313.15 K;▼323.15K

從表4可見，方程(6)中的參數A和B都與溫度成線性關系，可用下面的經驗方程表示：

將A對T作線性擬合，得到q0=－0.4835 L1/2·mol－1/2，q=0.0014L1/2·mol－1/2·K－1，擬合相關系數的平方

1r2=0.990，擬合的標準偏差s=2.1×10－3L1/2· mol－1/2。將粘度B系數對T作線性擬合，得到q2= 4.6039 L·mol－1，q3=－0.0111 L·mol－1·K－1，擬合相關系數的平方r2=0.993，擬合標準偏差s=0.013 L·mol－1。將方程(7)和(8)代入方程(6)則得到：

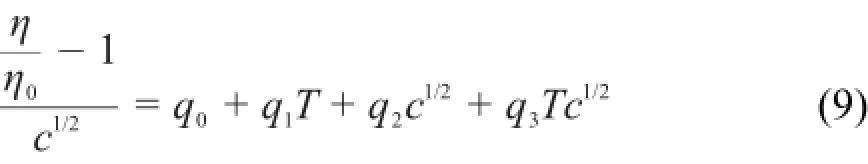
用方程(9)能夠在288.15－328.15 K溫度范圍內，預測濃度小于1mol·kg－1的[C2m im][A la]水溶液的粘度(見表S5(Supporting Information))，將預測值ηpre對相應的實驗值ηexp作圖(見圖3)，能得到斜率近似為1的直線。

3.3 離子液體水溶液的流動活化參數

Feakins等18,19在Eyring液體過渡狀態理論23基礎上推導出定量描述無限稀釋溶液的粘度B系數與液體流動活化自由能間的關系式：

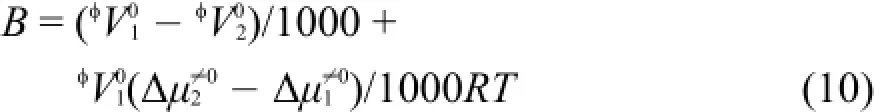
其中φ分別為溶劑和溶質摩爾體積為溶劑的摩爾流動活化自由能，為溶質對溶液活化自由能的貢獻。王健吉等24,25指出方程(10)中值可以用Eyring過渡狀態理論公式計算：

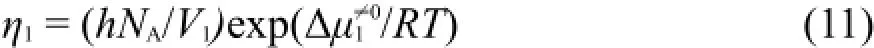
其中h為Planck常數，NA為Avogadro常數，V1為溶劑水的摩爾體積。把按方程(11)計算的Δμ1≠0和按方程(10)計算的Δμ2≠0值均列入表5中。

從表5中可見，Δμ2≠0隨溫度的變化可用下面的經驗方程描述：

表4 288.15－328.15K時[C2m im][A la]溶液的參數A，粘度B系數及相關系數平方r2和標準誤差sTable4 Parameter A,B coefficientof viscosity for aqueous[C2m im][Ala]with the correlation coefficien t square r2and the standard deviation s at 288.15－328.15 K

圖3 [C2m im][A la]溶液粘度預測值ηpre對實驗值ηexp作圖Fig.3 Plotting pred icted valuesof viscoity,ηprefor theaqueous[C2m im][Ala]vs the corresponding experimentalvalues,ηexpηpre=5.29×10－6+0.995ηexp;r2=0.9998;s=6.33×10－6Pa·s.■288.15K;●293.15K;▲298.15 K;▼303.15K;◆308.15K;?313.15K;?318.15 K;■323.15 K;★328.15 K

其中ai(i=0,1)是經驗參數。根據方程(12)，擬合Δμ2≠0和T，可以得到ai(i=0,1)的值：a0=(511.4± 6.7)kJ·mol－1；a1=(－1.023±0.022)kJ·K－1·mol－1；擬合相關系數平方為0.994，標準偏差是±0.84 kJ· mol－1。根據熱力學關系，溶液粘性流動的其它活化函數：活化熵(ΔS2≠0)和活化焓(ΔH2≠0)可以用下述方程來計算：

根據方程(13)和(14)計算的結果列在表5中，從表5中可以看出在給定質量摩爾濃度的溶液中，活化[C2m im][A la]溶液粘性流體的活化焓，ΔH2≠0，幾乎是與溫度無關的常數，因此摩爾活化熱容這表明對[C2m im][A la]溶液粘性流體的活化過程是一個等庫侖反應26(等庫侖反應指的是帶電粒子數和電荷相同的反應雙方。這種典型的反應往往有近零的熱容量變化，從而隨著溫度的升高具有恒定的焓變)。

3.4 預測溶液粘度的半經驗方法

Eyring23將他的反應速率的過渡狀態理論推廣到液體的輸運現象中，得到了一個簡單的粘度方程：

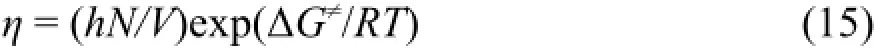
其中η為粘度，ΔG≠和V分別為液體粘性流動的活化Gibbs自由能和摩爾體積。這個方程不僅能夠解釋液體的粘度η隨溫度T的變化規律，而且還可以用它處理溶液的粘度。在二元溶液中應用，方程(15)中的V應改為溶液的平均摩爾體積Vm，其中ΔG≠為溶液粘性流動的平均活化Gibbs自由能，其定義為：其中分別為溶劑和溶質對平均活化Gibbs自由能ΔG≠的貢獻。如果把換成與濃度無關標準狀態的則方程(16)變為：

其中ΔμE≠為過量活化Gibbs自由能，ΔμE≠與體系過量Gibbs自由能GE有類似的意義22，這樣一來方程(15)可以寫成：

取對數：

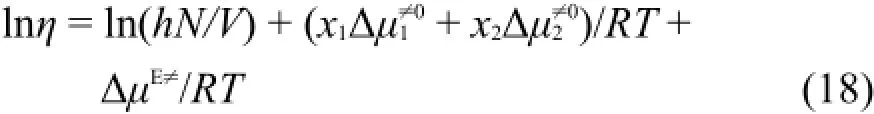
利用粘度實驗值η、Δμ1≠0和Δμ2≠0計算ΔμE≠/RT值并將其列入表6中。表6中的ΔμE≠/RT和溶液濃度m關系可以用下面經驗方程表示：

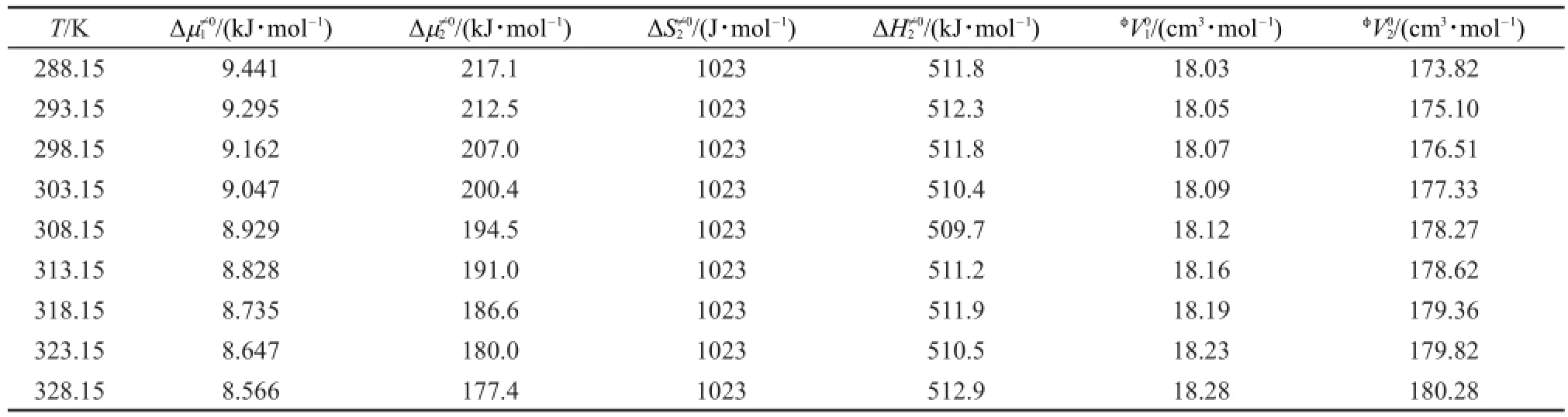
表5 [C2m im][Ala]水溶液粘性流動的活化熱力學參數Tab le5 Thermodynam ic parametersof theactivation for viscous flow of aqueous[C2m im][A la]

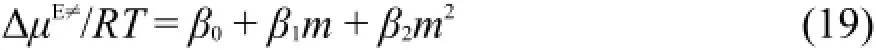
表6 [C2m im][A la]水溶液的ΔμE≠/RT值Table6 ValuesofΔμE≠/RT of aqueous[C2m im][Ala]

其中βi(i=0,1,2)是經驗常數。按方程(19)將ΔμE≠/ RT vsm擬合，擬合相關系數的平方大于0.99，說明方程(19)能夠很好地描述ΔμE≠/RT和溶液濃度m關系。將得到的經驗常數值βi、擬合相關系數的平方r2和擬合標準偏差s列入表6的底部。將方程(18)和方程(19)結合得到預測溶液粘度的新Eyring半經驗方程：

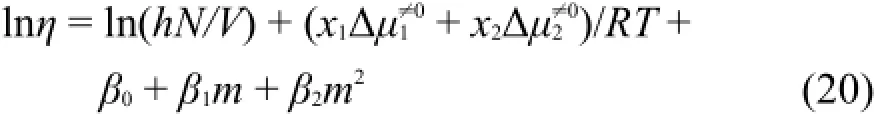
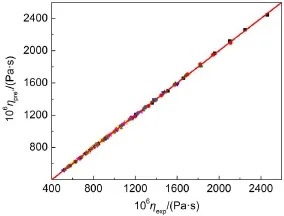
圖4 用Eyring半經驗方程預測的溶液粘度值ηpre′對實驗值ηexp作圖Fig.4 Plotting the viscosity values,ηpre′,of aqueous [C2m im][A la]estimated by using the sem i-empirical method vs the corresponding experimentalones,ηexpηpre′=－3.32×10－9+1.001ηexp;r2=0.9998;s=6.1×10－6Pa·s.■288.15K;●293.15K;▲298.15 K;▼303.15K;◆308.15K;?313.15 K;?318.15 K;■323.15 K;★328.15 K

將計算得到的溶液粘度的預測值ηpre′列入表S6 (Supporting Information)中。用新Eyring半經驗方程預測溶液粘度值ηpre′，用預測值對實驗值ηexp作圖能夠得到一條很好直線(見圖4)，其斜率接近1，相關系數平方為0.9998，說明用半經驗方程預測的溶液粘度與相應的實驗值十分相似，說明新Eyring半經驗方程是預測[C2m im][A la]水溶液粘度的有用工具。

4 結論

在288.15－328.15 K溫度范圍內測定了不同濃度氨基酸離子液體[C2m im][Ala]水溶液密度和粘度，Jones-Dole方程能很好地適用于離子液體[C2m im][A la]水溶液并獲得了粘度B系數，根據Feakins理論，得到了離子液體[C2m im][A la]對溶液粘滯流動活化自由能的貢獻和溫度之間的線性關系，進而得到了活化熵和活化焓在恒定溶液濃度的條件下，基本不隨溫度變化，這說明離子液體[C2m im][A la]水溶液粘滯流動活化過程是等庫侖反應。在Eyring過渡狀態理論基礎上本文提出了一個預測溶液粘度新方法，用這個新方法預測離子液體[C2m im][A la]水溶液的粘度值，與相應的實驗值相比十分類似。到目前為止，對溶液粘度的研究和預測多集中于單一電解質溶液，很少有人預測多組分電解質溶液的粘度27,28。然而，本文提出的新方法能夠很容易推廣到混合電解質溶液中，其預測方程為：

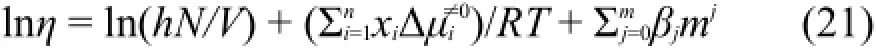
其中下角標i代表物種，i=1為溶劑，其余為溶質，n為溶液中的物種數；j+1代表多項式的項數。

Supporting In form ation:1H NMR of[C2m im][A la];the values of molar volume,Vm,and the apparent molar volume,?VB,for aqueous[C2mim][A la]with variousmolalities at 288.15－328.15 K;the values of concentration of substance,c, theextrapolation function,η′,the predicted values,ηpre,andηpre′for aqueous[C2m im][Ala];plottingη′vs c1/2at T=288.15, 298.15,308.15,318.15,328.15 K have been included.This information is available free of charge via the internet at http:// www.whxb.pku.edu.cn.

(1)Zhang,S.;Wang,J.;Lu,X.;Zhou,Q.Structures and InteractionsofIonic Liquids;Springer:Heidelberg,Germany, 2014.doi:10.1007/978-3-642-38619-0

(2)Greaves,T.L.;Drummond,C.J.Chem.Rev.2007,108(1),206. doi:10.1021/cr068040u

(3)Rantw ijk,F.V.;Sheldon,R.A.Chem.Rev.2007,38(107), 2757.doi:10.1021/cr050948h

(4)Tariq,M.;Freire,M.G.;Saramago,B.;Coutinho,J.A.P.; Lopes,J.N.C.;Rebelo,L.P.N.Chem.Soc.Rev.2011,41,829. doi:10.1039/c1cs15146k

(5)Sun,X.;Luo,H.;Dai,S.Chem.Rev.2012,112,2100. doi:10.1021/cr200193xd

(6)Riyazuddeen;Usmani,M.A.J.Chem.Eng.Data 2011,56, 3504.doi:10.1021/je2000205

(7)Liu,W.;Zhao,T.;Zhang,Y.;Wang,H.;Yu,M.J.So lut.Chem. 2006,35,1337.doi:10.1007/s10953-006-9064-7

(8)Tao,G.H.;He,L.;Liu,W.S.;Xu,L.;Xiong,W.;Wang,T.; Kou,Y.Green Chem.2006,8,639.doi:10.1039/b600813e

(9)Fukumoto,K.;Ohno,H.Chem.Commun.2006,3081.

(10)Fukumoto,K.;Yoshizawa,M.;Ohno,H.J.Am.Chem.Soc. 2005,127,2398.doi:10.1021/ja043451i

(11)Ohno,H.;Fukumoto,K.Acc.Chem.Res.2007,40,1122. doi:10.1021/ar700053z

(12)Tong,J.;Hong,M.;Chen,Y.;Wang,H.;Guan,W.;Yang,J.Z.J. Chem.Thermodyn.2012,54,352.doi:10.1016/j.jct.2012.05.012

(13)Hong,M.;Sun,A.;Yang,Q.;Guan,W.;Tong,J.;Yang,J.Z.J. Chem.Thermodyn.2013,67,91.doi:10.1016/j.jct.2013.07.008

(14)Hong,M.;Sun,A.;Liu,C.;Guan,W.;Tong,J.;Yang,J.Z.Ind. Eng.Chem.Res.2013,52,15679.doi:10.1021/ie402890r

(15)Hong,M.;Liu,R.J.;Yang,H.X.;Guan,W.;Tong,J.;Yang,J. Z.J.Chem.Thermodyn.2014,70,214.doi:10.1016/j. jct.2013.11.004

(16)Tong,J.;Liu,Q.S.;Zhang,P.;Yang,J.Z.J.Chem.Eng.Data 2007,52,1497.doi:10.1021/je700102g

(17)Jenkins,H.D.B.;M arcus,Y.Chem.Rev.1995,95,2695. doi:10.1021/cr00040a004

(18)Feakins,D.;Freemantle,D.J.;Law rence,K.G.J.Chem.Soc. Faraday Trans.I1974,70,795.doi:10.1039/f19747000795

(19)Feakins,D.;Waghorne,W.E.;Law rence,K.G.J.Chem.Soc. Faraday Trans.I 1986,82,563.doi:10.1039/f19868200563

(20)Lide,D.R.Handbook ofChemistryand Physics,82nd ed.;CRC Press:Boca Raton,2001.

(21)Huang,Z.Q.An Introduction to the Theory ofElectrolyte Solution,revised ed.;Science Press:Beijing,1983.[黃子卿.電解質溶液理論導論,修訂版.北京:科學出版社,1983.]

(22)Harned,H.S.;Owen,B.B.The PhysicalChemistry of Electro lyte Solutions,3rd ed.;Reinhold:New York,1958. doi:10.1149/1.2427250

(23)Eyring,H.J.Chem.Phys.1936,4,283.doi:10.1063/1.1749836

(24)Liu,W.B.;Wang,J.J.;Wang,C.L.;Lu,J.S.Acta Phys.-Chim. Sin.1992,8,742.[劉文彬,王健吉,王彩蘭,盧俊梭.物理化學學報,1992,8,742.]doi:10.3866/PKU.WHXB19920606

(25)Liu,W.B.;Wu,Y.P.;Wang,J.J.;Lu,J.S.Acta Phys.-Chim. Sin.1995,11,590.[劉文彬,吳艷平,王健吉,盧俊梭.物理化學學報,1995,11,590.]doi:10.3866/PKU.WHXB19950705

(26)Mountain,B.W.;Seward,T.M.Geochimica etCosmochimica Acta 2003,67,3005.doi:10.1016/S0016-7037(00)00303-X

(27)Hu,Y.F.;Lee,H.Electrochim Acta 2003,48,1789. doi:10.1016/j.electacta.2003.03.002

(28)Hu,Y.F.Chem.Eng.Sci.2004,59,2457.doi:10.1016/j. ces.2003.11.005

Parameters of the Activation of Viscous Flow of Aqueous[C2mim][Ala]

TONG Jing*LIU Lu ZHANG Duo ZHENG Xu CHEN Xia YANG Jia-Zhen
(College ofChemistry,Liaoning University,Shenyang 110036,P.R.China)

The density and viscosity ofaqueous solutions ofan ionic liquid(IL)based on alanine,[C2m im][Ala], w ith variousmola lities w erem easured in the tem perature range of T=288.15－328.15 K w ith inte rvals of5 K. From the Jones-Dole equation,a viscosity B-coefficientwith a large positive value and d B/d T＜0 were obtained. According to Feakins,the contribution of the solute to the activation free energy for viscous flow of the solution, Δμ2≠0,was ob tained.The rela tionship betweenΔμ2≠0and tem peratu re w as linea r,a llow ing the standard m ola r activation entropy,ΔS2≠0,and enthalpy,ΔH2≠0,to be obtained.On the basis of Eyring′s theory,a new sem i-empirical method to estimate the viscosity ofaqueous[C2m im][Ala]was proposed.The values estimated using thismethod agreed wellw ith the corresponding experimentalones.

Ionic liquid;Viscosity ofsolution;Viscosity B-coefficient;Activation parameter for viscous flow ofsolution;Transition-state theory

.Email:tongjinglnu@sina.com;Tel:+86-24-62207801.

Theprojectwas supported by theNationalNatural Science Foundation of China(21273003).

國家自然科學基金(21273003)資助項目?Editorialoffice of Acta Physico-Chim ica Sinica

O642

10.1039/b606613e

doi:10.3866/PKU.WHXB201610251

www.whxb.pku.edu.cn

Received:September13,2016;Revised:October25,2016;Published online:October25,2016.*