第32屆CMO平面幾何題探源
陳 婧
江蘇省南京市鼓樓實驗中學 (210000)
第32屆CMO平面幾何題探源
陳 婧
江蘇省南京市鼓樓實驗中學 (210000)
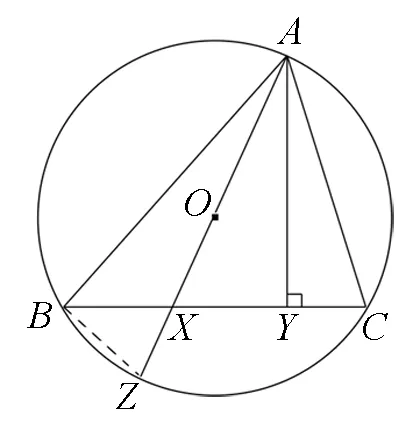
圖1
原題 如圖1,AY是ΔABC的高,AZ是ΔABC的外接圓⊙O的直徑,且AZ與BC相交于點X.求證:AB·AC=AY·AZ.

這是蘇教版普通高中課程標準實驗教科書數學選修4-1《幾何證明選講》中的一道經典例題,由于從三角形一個頂點所作外接圓的直徑和對邊上的高恰巧是這個內角的兩條等角線(外心與垂心是等角共軛點),所以本例題備受奧賽命題專家與數學愛好者的青睞.下面,讓我們來看看它是如何演化為2016年第32屆中國數學奧林匹克(CMO冬令營)平面幾何試題的.
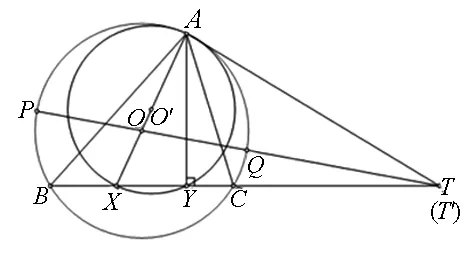
圖2
如圖2(在圖1的基礎上),作RtΔAXY的外接圓⊙O′(直徑為AX),由OO′=OA-O′A,知⊙O與⊙O′內切于點A,過點A作⊙O與⊙O′的外公切線AT交直線BC于點T,設直線TO與⊙O交于點P、Q,則由射影定理與切割線定理得,TX·TY=TA2=TB·TC=TP·TQ,故P、Q、X、Y四點共圓.
反之,設PQ是⊙O的任意一條直徑,且PQ所在直線與直線BC交于點T′,當P、Q、X、Y四點共圓(此圓設為⊙O″)時,由根心定理可知,⊙O與⊙O′的外公切線AT、⊙O′與⊙O″的公共弦XY所在直線以及⊙O與⊙O″的公共弦PQ所在直線交于點T(根心),即點T′與點T重合.

圖3
如圖3(在圖2的基礎上),過點T作⊙O的另一條切線TS(S為切點),連結AS,交PQ于點E,交BC于點D,即知TO⊥AS于點E,從而知TE·TO=TA2=TB·TC,故B、O、E、C四點共圓.設分別過點B、C且與⊙O相切的直線交于點L,連結OB、OC、OL,注意到∠OBL+∠OCL=180°,即知B、O、C、L四點共圓且OL為該圓的直徑,于是B、O、E、C、L五點共圓.連結EL,則∠OEL=90°=∠OES,故A、E、D、S、L五點共線.


設想點I在直徑PQ上,且P、Q、X、Y四點共圓(特殊化試探),則點T′與點T重合,注意到AL⊥OT,AL⊥IT,結合調和點列、調和線束的性質知,AL為T關于圓I的極線,從而知圓I與BC的切點在極線AL上,故點D為切點,即A、D、L三點共線.
反之,設想點I在直徑PQ上,且A、D(D為圓I與BC的切點)、L三點共線(特殊化試探),則B、D、C、T′為調和點列,故AD為T′關于圓I的極線,于是OT′⊥AL,IT′⊥AL,從而O、I、T′三點共線,進而知點T′與點T重合,于是P、Q、X、Y四點共圓.
通過上面的討論,即可生成2016年11月在湖南長沙市雅禮中學舉行的第32屆中國數學奧林匹克(CMO冬令營)第2道賽題(平面幾何題):
賽題 如圖4,銳角ΔABC中,外心為O,內心為I,過點B、C作外接圓的切線交于點L,內切圓切BC于點D,AY垂直BC于點Y,AO交BC于點X.PQ為過點I的圓O的直徑.求證:P、Q、X、Y四點共圓等價于A、D、L三點共線.
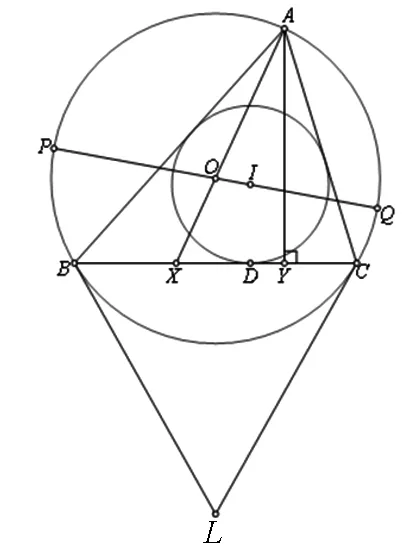
圖4

