函數中無處不在的最值問題

☉江蘇省揚中高級中學 范 麗

函數中無處不在的最值問題

☉江蘇省揚中高級中學 范 麗

函數的最值問題一直是高考考查的重點.最值問題可以衍生出許多其他問題，其中的題型千變萬化，而這也給函數最值問題的學習增加了很大難度.即便如此，只要學生平時做好積累、勤加練習、及時總結和歸納，函數的最值問題便不會成為學習上的攔路虎.

一、三角函數的最值問題

三角函數的最值問題也是高考中的重要考點，這種問題一般都需要對三角函數式進行恒等變形，將原三角函數轉化成可以直接求最值的函數，下面的例子就是通過對原三角函數進行恒等變形求最值的典型例題.

例1求函數y=5sinx+cos2x的最值.

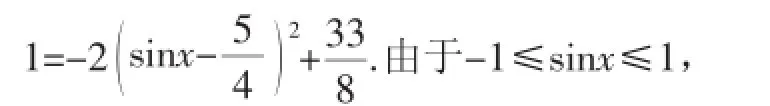
所以當sinx=-1時，ymin=-6；當sinx=1時，ymax=4.

所以函數y=5sinx+cos2x的最大值為4，最小值為-6.

點撥：本題如果用常規的求導法求解，求解過程會非常煩瑣，此時明智的做法是通過恒等變形，將原三角函數式進行轉化，通過熟悉的函數來求最值，從而使解題過程大大簡化，達到事半功倍的效果.

二、二次函數的最值問題

高考對二次函數的考查屢見不鮮，求二次函數的最值問題更是常見.但是此類問題不是單純考查二次函數的最值，而是要確定在某區間內的最值，有時候區間還含有未知數，這就給解題帶來了很大難度.這種問題一般通過分類討論的方法來解決，通過下面的例子可以來了解這類問題.

例2（2016年揚州高考二模第23題）已知函數f（x）=x2-7x+15，求f（x）在x∈［t，t+1］上的最大值.

解析：本題若沒有x∈［t，t+1］這一限制條件，而是一個確定的范圍，則問題非常簡單，只要根據函數的單調性，就可以求出函數的最值.但是有了這個限制條件之后，問題就變得比較復雜，需要進行分類討論.

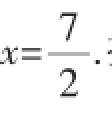
綜上所述，當t＞3時，f（x）的最大值為f（t+1）=t2-5t+9；當t≤3時，f（x）的最大值為f（t）=t2-7t+15.

點撥：本題是通過導數法求二次函數最值的典型例題，但是由于所求最值的區間含有未知數，給解題平添許多難度，解決此題需要對含有未知數的區間進行分類討論.但是只要根據函數的對稱軸，按部就班地對未知數的取值進行討論即可，盡管過程比較復雜，但是也可以得到想要的結果.

三、對數型函數的最值問題

初等函數與對數函數復合構成對數型函數，由于對數函數的單調性，使得這類問題千變萬化.對數型函數的最值問題也很常見，一般是通過函數的單調性來考查最值，通過下面的例子可以深入了解此類對數型函數求最值的問題.

例3求函數f（x）=log2（-x2-4x+12）的最大值.

解析：本題首先應該通過換元將二次函數轉化為一次函數，然后再利用對數函數的單調性進行求解.可令μ=-x2-4x+12=-（x+2）2+16，易得0＜μ≤16.因為y=log2μ在（0，+∞）上為增函數，所以log2μ≤log216=4.所以f（x）的最大值為4.

點撥：本例通過換元法將對數式中的二次函數進行轉化，使得函數變成一般的對數函數，通過對數函數的單調性，只要求出換元之后函數μ的最值，那么f（x）的最值問題也就迎刃而解了.

四、不規則函數的最值問題

對于一些不規則函數的最值問題，最基本的方法就是導數法，通過求導數判斷函數的單調性.有時不規則函數中含有參數，這類問題就需要分類討論，根據對參數的分類討論，從而得出函數的最值.下面的例子就是關于此類問題的一道綜合題，比較具有代表性.

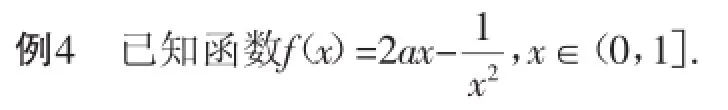
（1）若f（x）在（0，1］上是增函數，求實數a的取值范圍；

（2）求f（x）在區間（0，1］上的最大值.

解析：本題是一般函數單調性問題，可以通過導數法進行求解，但是在解題過程中有一些細節需要引起學生的注意.

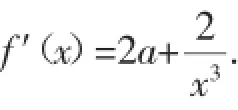
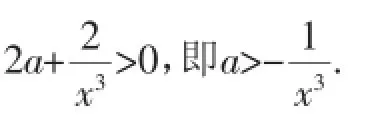
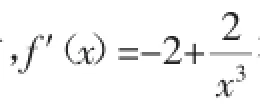
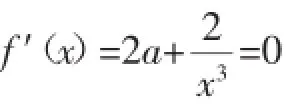
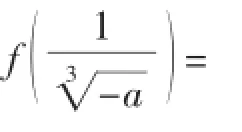
點撥：本例的解題過程比較復雜，但是只要抓住參數的取值這條主線，按部就班他進行分類討論，相對復雜的問題也是可以得到解決的.需要注意的一點是，對于比較難的綜合題，第（1）問一般是第（2）問的鋪墊，通過仔細研究第（1）問，會對比較有難度的第（2）問的解決產生較大幫助.

綜上所述，高中數學中對于函數最值問題的考查非常頻繁，這也是高考中的重點內容，這類問題一般綜合性比較強，解決此類問題需要扎實的基礎知識，這需要學生在平時的學習中多加聯系，認真總結和歸納，而老師也應該做好必要的引導工作.

1.陳春明.善用最值另辟蹊徑——例談函數最值的運用［J］.中學數學（上），2016（11）.

2.陳亞琴.三角函數的求解方法概覽［J］.中學數學（上），2014（10）.

3.劉馨憶.導數視角下函數最值問題的轉化求解［J］.中學數學（上），2016（6）.