基于支持向量機的庫克群島海域長鰭金槍魚棲息環(huán)境綜合指數(shù)

宋利明，周建坤，沈智賓，趙海龍，謝凱

（1.上海海洋大學海洋科學學院，上海201306；2.國家遠洋漁業(yè)工程技術(shù)研究中心，上海201306；3.大洋漁業(yè)資源可持續(xù)開發(fā)省部共建教育部重點實驗室，上海201306；4.遠洋漁業(yè)協(xié)同創(chuàng)新中心，上海201306）

基于支持向量機的庫克群島海域長鰭金槍魚棲息環(huán)境綜合指數(shù)

宋利明1，2，3，4，周建坤1，沈智賓1，趙海龍1，謝凱1

（1.上海海洋大學海洋科學學院，上海201306；2.國家遠洋漁業(yè)工程技術(shù)研究中心，上海201306；3.大洋漁業(yè)資源可持續(xù)開發(fā)省部共建教育部重點實驗室，上海201306；4.遠洋漁業(yè)協(xié)同創(chuàng)新中心，上海201306）

掌握海洋環(huán)境因子對長鰭金槍魚（Thunnus alalunga）資源密度分布的影響有利于該資源的可持續(xù)利用。根據(jù)2013年9-12月在庫克群島海域利用延繩釣調(diào)查所獲得的共計56個站點的長鰭金槍魚漁獲率數(shù)據(jù)，以及測得的溫度、葉綠素a濃度、水平海流及垂直海流等環(huán)境因子數(shù)據(jù)，采用支持向量機方法分析了各水層（40.0~239.9 m，每40 m為一層）及整個水體中各個環(huán)境因子與長鰭金槍魚漁獲率的關系并建立了長鰭金槍魚棲息環(huán)境綜合指數(shù)（IHI）模型，并利用驗證站點對模型進行了驗證。結(jié)果表明：（1）預測漁獲率與其對應的名義漁獲率無顯著性差異；（2）IHI模型的預測能力較好，能有效預測長鰭金槍魚的分布；（3）不同水層影響長鰭金槍魚分布的主要因素不同，在40.0~79.9 m、80.0~119.9 m、120.0~159.9 m、160.0~199.9 m和200.0~239.9m水層其分布分別主要受葉綠素a濃度、水溫、垂直海流、葉綠素a濃度和溫度的影響。整個水體影響長鰭金槍魚分布的主要因素為溫度；（4）長鰭金槍魚分布密度較高的水層為120.0~199.9 m；（5）長鰭金槍魚IHI指數(shù)分布較高的3個區(qū)域分別為9°00′S-12°20′S，159°00′W-164°00′W、13°30′S-14°30′S，159°00′W-161°00′W和10°30′S-12°30′S，167°00′W-168°00′W，建議在上述海域作業(yè)時，應使釣具沉降到120~199.9 m水層，以減少其它物種的兼捕率并提高長鰭金槍魚的漁獲率。

長鰭金槍魚；棲息環(huán)境綜合指數(shù)；支持向量機；庫克群島

長鰭金槍魚（Thunnus alalunga）是庫克群島海域延繩釣漁業(yè)的主要捕撈對象之一（陳錦淘等，2005；Wu et al，2009；范江濤等，2011）。影響長鰭金槍魚漁獲率的環(huán)境因子很多，涉及水溫、鹽度、葉綠素a濃度和溶解氧等（Roberts，1980；Laurs et al，1984；Chien et al，2006；周甦芳等，2006；Zainuddin et al，2004；2006；2008；Hoyle et al，2009；楊嘉樑等，2014）。Roberts等（1980）通過研究長鰭金槍魚資源分布與海表水溫的關系，指出長鰭金槍魚幼體一般生活在海表水溫為18.5℃~21.3℃的海域，并且溫躍層的深度也對長鰭金槍魚的漁獲率有較大影響。Murray等（1994）研究發(fā)現(xiàn)，南太平洋海域長鰭金槍魚集中分布在200~300 m深的水層，該水層為鹽度與溫度強弱交匯處，溫度為9℃~20℃。一些學者使用遙感數(shù)據(jù)對長鰭金槍魚漁場分布進行分析（Zainuddin et al，2004；2006；2008；樊偉等，2007；陳雪忠等，2013）。楊嘉樑等（2014）使用漁場環(huán)境、作業(yè)參數(shù)、漁獲統(tǒng)計數(shù)據(jù)，通過分位數(shù)回歸分析有關水層長鰭金槍魚漁獲率與溫度、鹽度、葉綠素a濃度和溶解氧等環(huán)境因子的關系，并考慮其不同的影響權(quán)重及交互作用建立了棲息環(huán)境綜合指數(shù)模型。很多學者通過廣義相加模型（Maunder et al，2004；Su et al，2008；Howell et al，2010）、隨機森林（陳雪忠等，2013）等統(tǒng)計模型對魚群分布進行預測。Harrell等（1996）的研究表明，在分析高維數(shù)據(jù)時，為了增加預測模型的準確度，自變量的個數(shù)不宜太多。在以往的研究中,普遍采用的是線性模型（Hinton et al，2004；Okamoto，2008），但是隨著漁業(yè)研究的不斷深入，傳統(tǒng)的線性模型已很難滿足當今漁業(yè)研究對精度的要求。Cortes等（1995）提出了支持向量機，把線性不可分空間產(chǎn)生一個最優(yōu)非線性決策邊界。本文利用支持向量機方法（Cortes et al，1995；張浩然等，2002；袁紅春等，2010）對庫克群島海域整個水體及不同水層的長鰭金槍魚棲息環(huán)境綜合指數(shù)進行分析研究，探討各環(huán)境因子對長鰭金槍魚資源分布的綜合影響，從而為該海域長鰭金槍魚資源的可持續(xù)利用提供參考。

1 材料與方法

1.1材料

1.1.1 調(diào)查船、調(diào)查時間及調(diào)查海域

參與調(diào)查的漁船“華南漁719”為低溫金槍魚延繩釣漁船，主要的船舶參數(shù)如下：總長36.60 m；型寬6.60 m；型深3.30 m；總噸196 t；凈噸89 t；主機功率440.00 kW。

調(diào)查時間為2013年9月8日到12月18日。調(diào)查范圍為9°06′S-18°04′S，157°05′W-167°46′W，共56個站點，隨機選定其中42個站點的數(shù)據(jù)用于建立預測模型，14個站點的數(shù)據(jù)用于模型的驗證（圖1）。

1.1.2 調(diào)查方法和內(nèi)容

本次調(diào)查的漁具、漁法、調(diào)查的儀器和調(diào)查內(nèi)容具體見文獻（宋利明等，2016）。本次調(diào)查測得的具有代表性的溫度、葉綠素a濃度、垂直海流以及水平海流隨水深的變化見圖2。

1.2數(shù)據(jù)處理方法

1.2.1 釣鉤深度的計算方法

釣具的理論深度按照吉原有吉的釣鉤理論深度計算公式（齋藤，1992）計算得出，具體計算公式如下：

圖1 建模站點和模型驗證站點建模站點模型驗證站點）

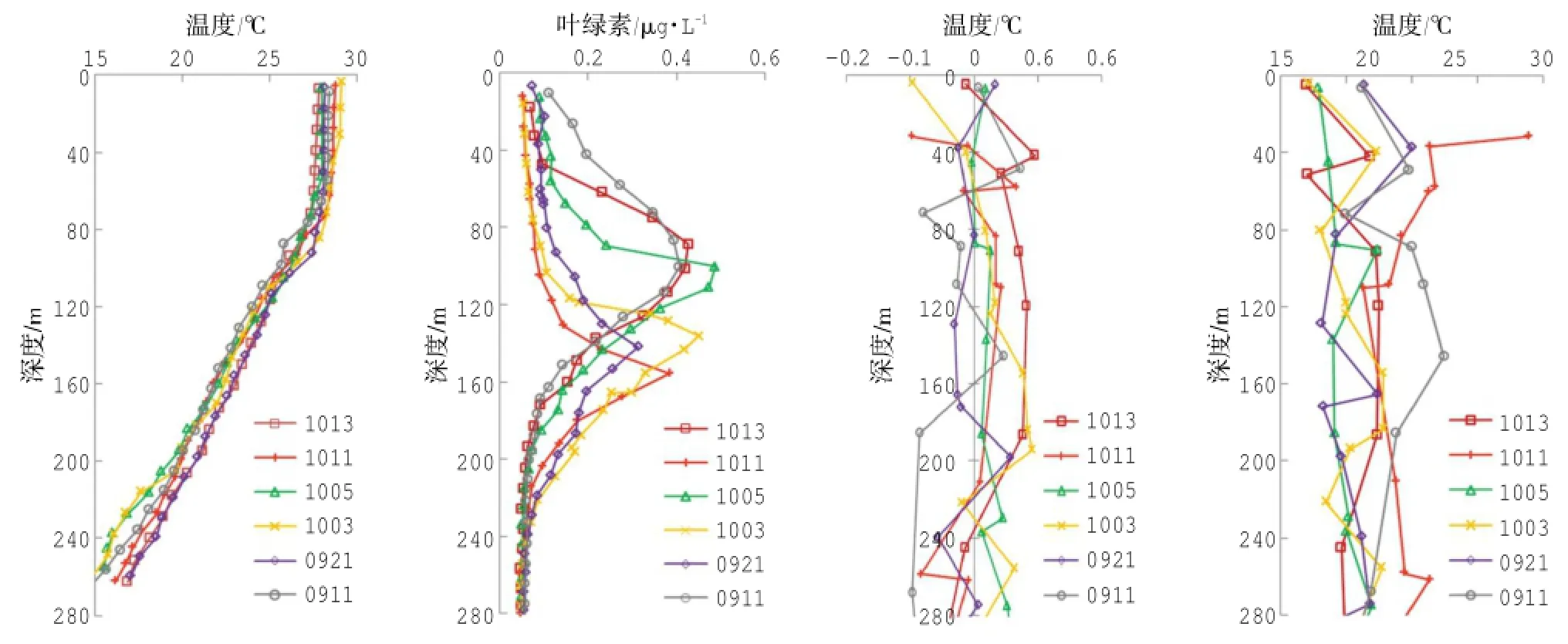
圖2 調(diào)查期間典型的溫度、葉綠素a濃度、垂直海流和水平海流垂直剖面圖

式（1）~（4）中，Dx為第x號釣鉤的理論深度（m）；ha為支繩長度（m）；hb為浮子繩長度（m）；l為干線弧長的一半（m）；φ0為干線與浮子繩連接點的切線與海平面的夾角（°），與式（4）中的短縮率k有關，現(xiàn)實中該角度難以測量，本研究利用計算短縮率k來推算出φ0；x為兩個浮子間釣鉤的編號；n為兩個浮子間干線的分段數(shù)；L為兩個浮子在海面上的水平距離（m）；t為投繩時前后2支繩之間相隔的時間間隔（s）；V1為投繩機出繩速度（m/s）；V2為航速（m/s）。

應用SPSS軟件，采用多元線性逐步回歸的方法建立釣鉤擬合深度與理論深度（D）x的關系模型。定義釣鉤實測深度（TDR所測深度）與理論深度的比值為釣鉤沉降率。認為釣鉤所能達到的深度（釣鉤擬合深度）等于釣鉤理論深度與擬合沉降率（回歸擬合得出的釣鉤沉降率）的乘積。釣鉤的沉降率受到釣具漂移速度（V）g、風速（Vw）、風流合壓角（γ）、風舷角（Qw）和鉤號（x）的影響，將以上參數(shù)取對數(shù)值作為自變量，以釣鉤沉降率的對數(shù)值作為因變量導入SPSS軟件中進行回歸，得出擬合沉降率計算公式，進而計算得到釣鉤擬合深度（式5）。其中，釣具漂移速度是指釣具在風、流的合力作用下，釣具在海中的對地漂移的速度（m/s）；風速：風速儀測得的風的速度（m/s）；風流合壓角是指釣具在海中的漂移方向與投繩航向之間的夾角（°）；風舷角是指風向與投繩航向之間的夾角（°）。

釣鉤擬合深度的最終計算公式為：

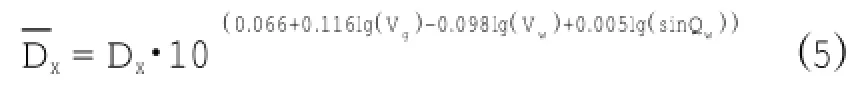
1.2.2 長鰭金槍魚漁獲率的計算方法

水深范圍為0~240 m，將整個水體分成6層，每一水層均為40 m。分別計算出調(diào)查期間各站點、各個水層的釣鉤數(shù)量、長鰭金槍魚的釣獲尾數(shù)。最終計算出各個站點、各水層長鰭金槍魚的漁獲率CPUE，計算公式如下（齋藤，1992；Wu et al，2009；宋利明等，2012）

式（6）中，Hij為第i站點、第j水層內(nèi)的釣鉤數(shù)量，其中i的取值范圍為1、2、3、…、55、56；j的取值范圍為1、2、…、5、6。56個站點釣獲的長鰭金槍魚共計2 880尾。

Nij為第i站點、第j水層釣獲的長鰭金槍魚的尾數(shù)，其具體計算公式如下：

式（7）中，Nj為整個調(diào)查期間第j水層所釣獲的長鰭金槍魚總尾數(shù)；N為調(diào)查期間長鰭金槍魚總釣獲尾數(shù)；Ni為第i站點所釣獲的長鰭金槍魚尾數(shù)。

長鰭金槍魚在第i站點的漁獲率CPUEi的計算方法如下（齋藤，1992；Wu et al，2009；Song et al，2011；宋利明等，2012）：

式（8）中，Hi為第i站點投放的釣鉤數(shù)量。

長鰭金槍魚在整個調(diào)查期間第j水層的漁獲率CPUEj的計算方法如下（齋藤，1992；Wu et al，2009；Song et al，2011；宋利明等，2012）：

Hj為整個調(diào)查期間第j水層內(nèi)投放的釣鉤數(shù)量。

1.2.3 環(huán)境因子平均值的計算方法

各個站點在每個水層的環(huán)境因子值Eij為每個水層內(nèi)儀器所采集的環(huán)境數(shù)據(jù)的算術(shù)平均值。該站點整個水體的環(huán)境因子值Ei通過該站點各水層內(nèi)環(huán)境因子的加權(quán)平均值計算而得，加權(quán)系數(shù)則為整個調(diào)查期間長鰭金槍魚在各個水層的漁獲率CPUEj（宋利明等，2011），具體計算公式如下：

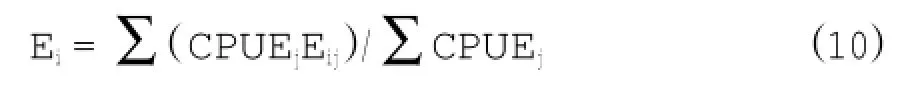
調(diào)查期間，在0~40 m這一水層內(nèi)無長鰭金槍魚漁獲物，這一水層的長鰭金槍魚的漁獲率為零，本研究僅建立了40.0~79.9 m（j=1）、80.0~119.9 m（j=2）、120.0~159.9 m（j=3）、160.0~199.9 m（j=4）和200.0~239.9 m（j=5）這5個深度范圍相應的CPUE預測模型并建立棲息環(huán)境綜合指數(shù)模型。

1.2.4 建立長鰭金槍魚CPUE預測模型

由于庫克群島海域長鰭金槍魚漁場是動態(tài)變化的，而對動態(tài)變化的相關經(jīng)驗知識不多，其中不確定因素較多，難以得出規(guī)律。所以本文采用支持向量機二分法的思想（Cortes et al，1995；張浩然等，2002；袁紅春等，2010），其最顯著的優(yōu)點為在長鰭金槍魚漁場先驗知識不足的情況下，通過各水層環(huán)境因子與對應實測CPUE數(shù)據(jù)的導入，并在可控范圍內(nèi)選取足夠訓練樣本后，可以智能選取與訓練樣本類似的其它數(shù)據(jù)向量。本文隨機選定42個站點的數(shù)據(jù)用于建立預測模型，以長鰭金槍魚的實測CPUE（CPUEi，CPUEij）、溫度（Ti，Tij）、葉綠素a濃度（Fi，F(xiàn)ij）、水平海流（Si，Sij）和垂直海流（Vi，Vij）按作業(yè)天為單位導入MATLAB中，得到與訓練樣本相似度較高的向量，然后用選出的高相似度向量（P≥0.05）在SPSS中擬合出預測CPUE與海洋環(huán)境因子的關系模型。預測CPUE與各海洋環(huán)境因子之間的關系假設為：

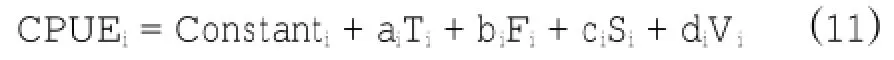
式（11）中，Constanti為常數(shù)項，其大小由支持向量機閾值決定，ai、bi、ci和di分別為溫度（Ti）、葉綠素a濃度（Fi）、水平海流（Si）和垂直海流（Vi）相應的系數(shù)，在SPSS中根據(jù)支持向量機模型原理擬合得出。

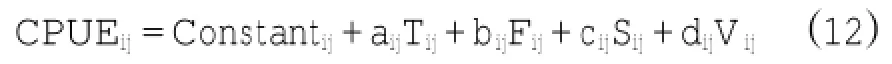
式（12）中，Constantij為常數(shù)項，其大小由支持向量機閾值決定，aij、bij、cij和dij分別為溫度（Tij）、葉綠素a濃度（Fij）、水平海流（Sij）和垂直海流（Vij）相應的系數(shù)，在SPSS中根據(jù)支持向量機模型原理擬合得出。

1.2.5 長鰭金槍魚棲息環(huán)境綜合指數(shù)（IHI）模型

根據(jù)上述建立的長鰭金槍魚在各個水層和整個水體的CPUE預測模型，將海洋環(huán)境因子分別輸入相應的CPUE預測模型中，得到長鰭金槍魚預測漁獲率，即CPUEi和CPUEij，然后計算棲息環(huán)境綜合指數(shù)IHIi和IHIij（宋利明等，2012），具體計算公式如下：

式（13）和（14）中，CPUEmax是CPUEi和CPUEij中的最大值。

1.2.6 IHI模型的驗證和預測能力的評價

將14個驗證站點對應的海洋環(huán)境數(shù)據(jù)導入預測模型中，計算出該14個驗證站點的預測CPUE，與實測的名義CPUE進行比對，作符號秩（Wilcoxon）檢驗來判定兩者是否存在顯著相關性（Wilcoxon，1945；Cortes et al，1995；張浩然等, 2002；袁紅春等，2010）。最后，分別計算出基于預測模型的長鰭金槍魚驗證站點整個水體和各水層的棲息環(huán)境綜合指數(shù)，使用Marine Explorer 4.0軟件繪制其分布圖，并與實測CPUE進行比對。

本文通過對模型建立站點各水層及整個水體的棲息環(huán)境綜合指數(shù)（IHI）及與其相對應的實測CPUE間的Spearman系數(shù)來評價模型的預測能力（Olds，1949；張利田等，2007）。

2 結(jié)果

2.1不同水層和整個水體中長鰭金槍魚的預測CPUE

通過支持向量機對各站點各個水層內(nèi)長鰭金槍魚的漁獲率與相關環(huán)境因子值（為各站點各個水層的平均溫度、葉綠素、水平海流和垂直海流）的選取，得出不同水層長鰭金槍魚CPUE預測模型，各水層預測模型的具體參數(shù)如表1。不同水層影響長鰭金槍魚分布的主要因素不同，在40.0~79.9 m、80.0~119.9 m、120.0~159.9 m、160.0~199.9 m和200.0~239.9 m水層其分布分別主要受葉綠素a濃度、水溫、垂直海流、葉綠素a濃度和溫度的影響。整個水體影響長鰭金槍魚分布的主要因素為溫度。

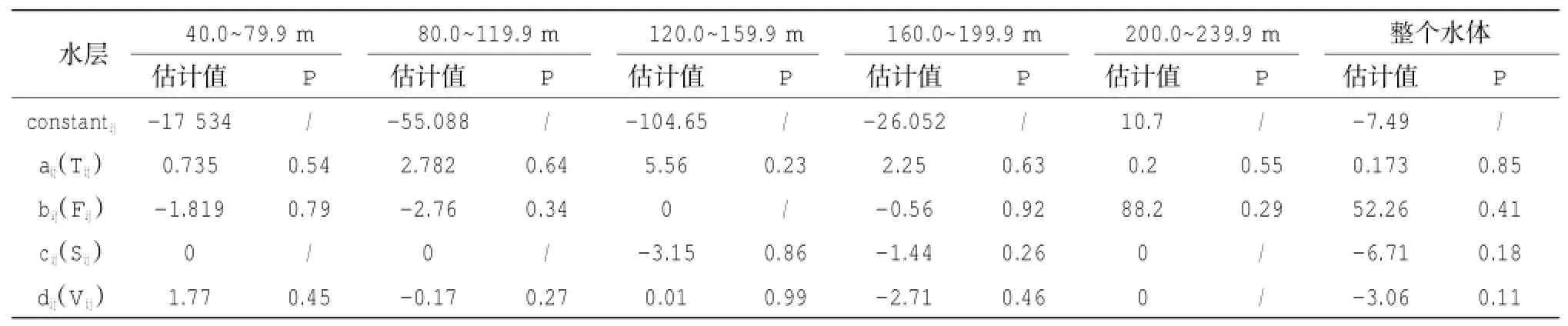
表1 各水層最佳CPUE預測模型的參數(shù)

2.2長鰭金槍魚棲息環(huán)境綜合指數(shù)（IHI）

將所得的預測CPUEij用于計算各水層的長鰭金槍魚棲息環(huán)境綜合指數(shù)，繪制棲息環(huán)境綜合指數(shù)分布與名義CPUE疊加圖，見圖3。從圖3中得出IHI指數(shù)較高的海域見表2。從表2可知，不同水層的IHIij指數(shù)存在較大的差異，其中120.0~199.9 m水層長鰭金槍魚的IHIij最高（0.40~0.80），而40.0~79.9m水層長鰭金槍魚的IHIij最低（0.08~0.16）。庫克群島海域整個水體中長鰭金槍魚和名義CPUE空間分布如圖4。IHIij和指數(shù)較高的范圍為9°00′S-12°20′S，159°00′W-164°00′W、13°30′S-14°30′S，159°00′W-161°00′W和10°30′S-12°30′S，167°00′W-168°00′W（表2）。

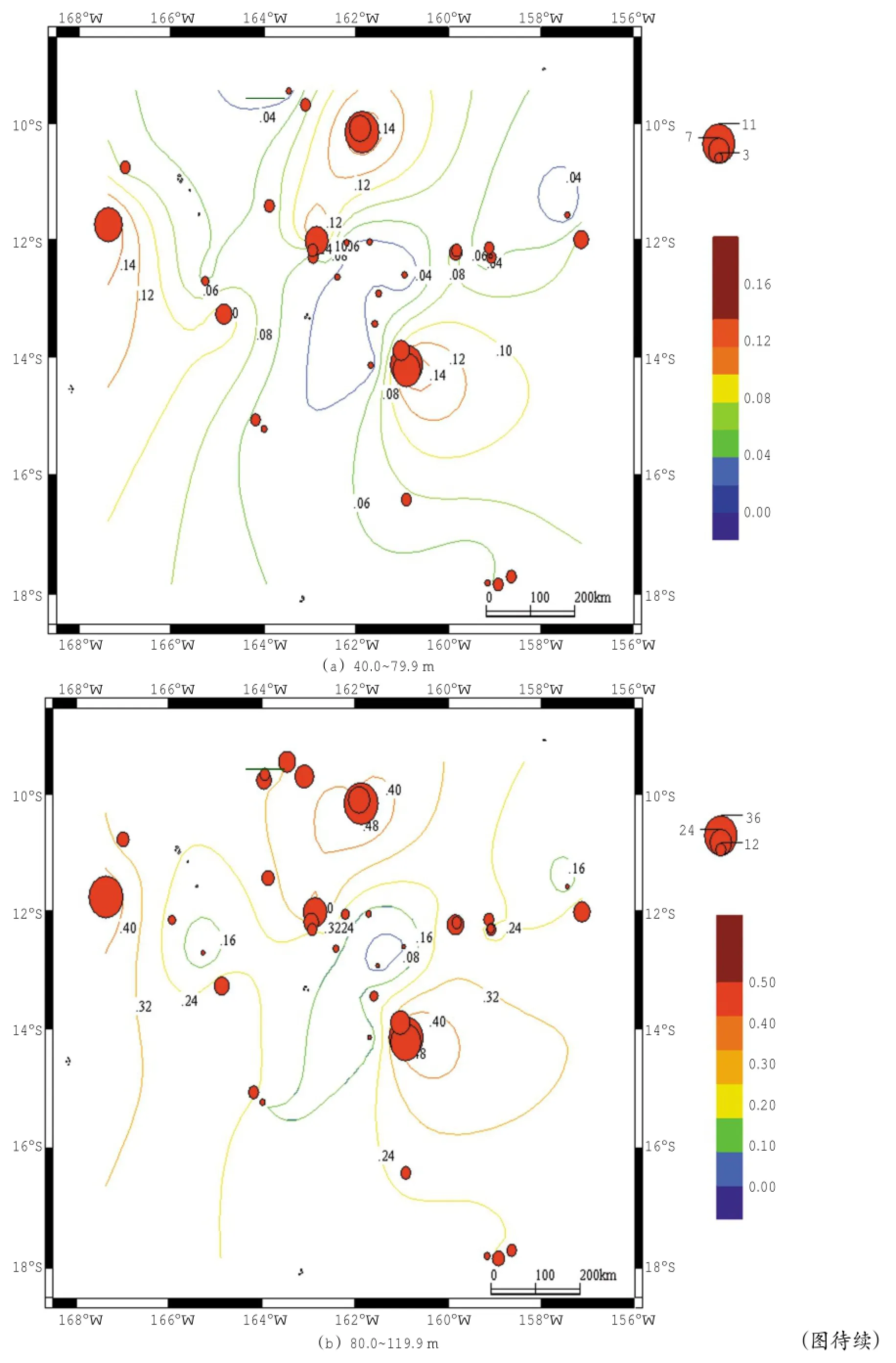
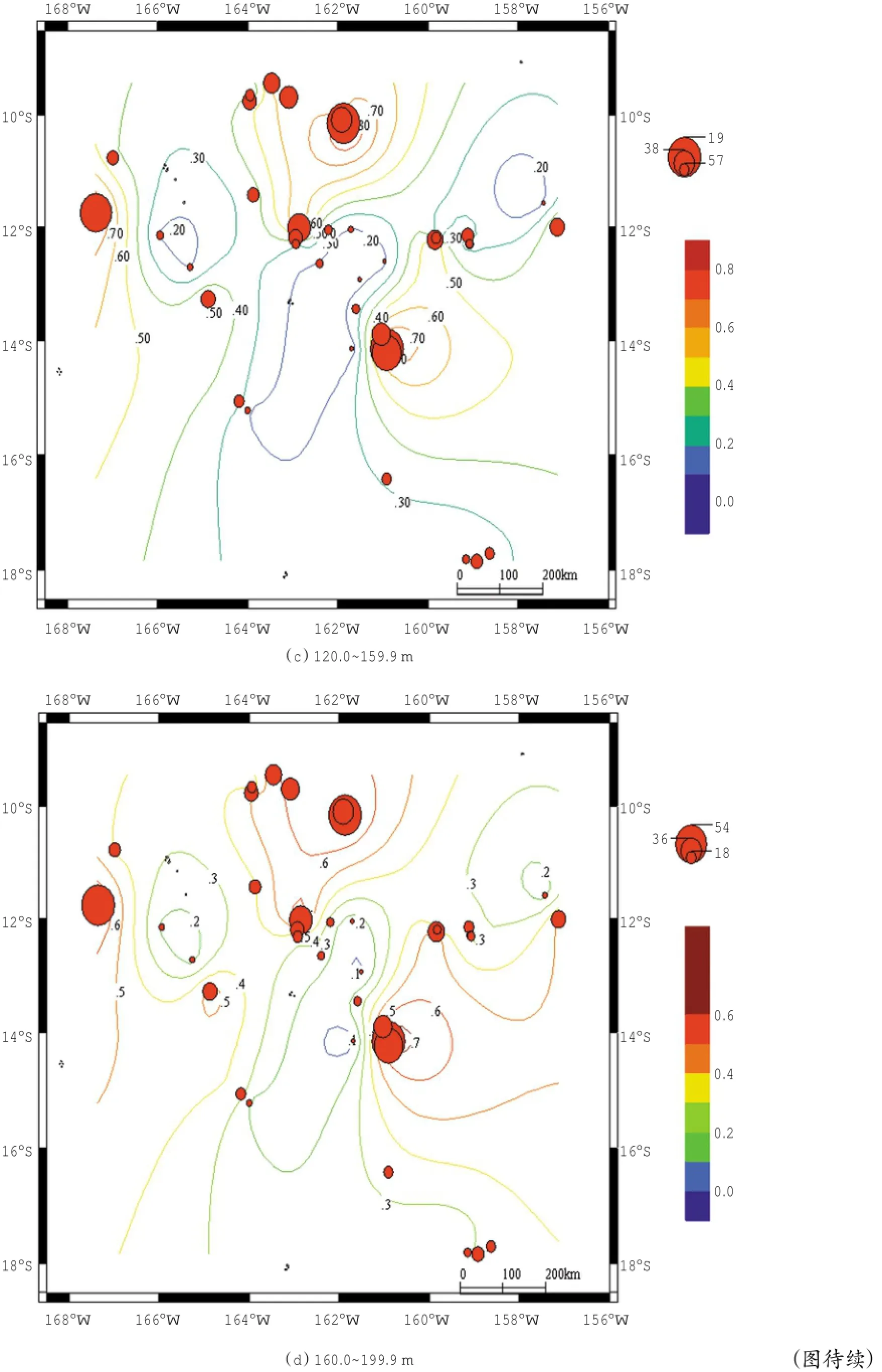
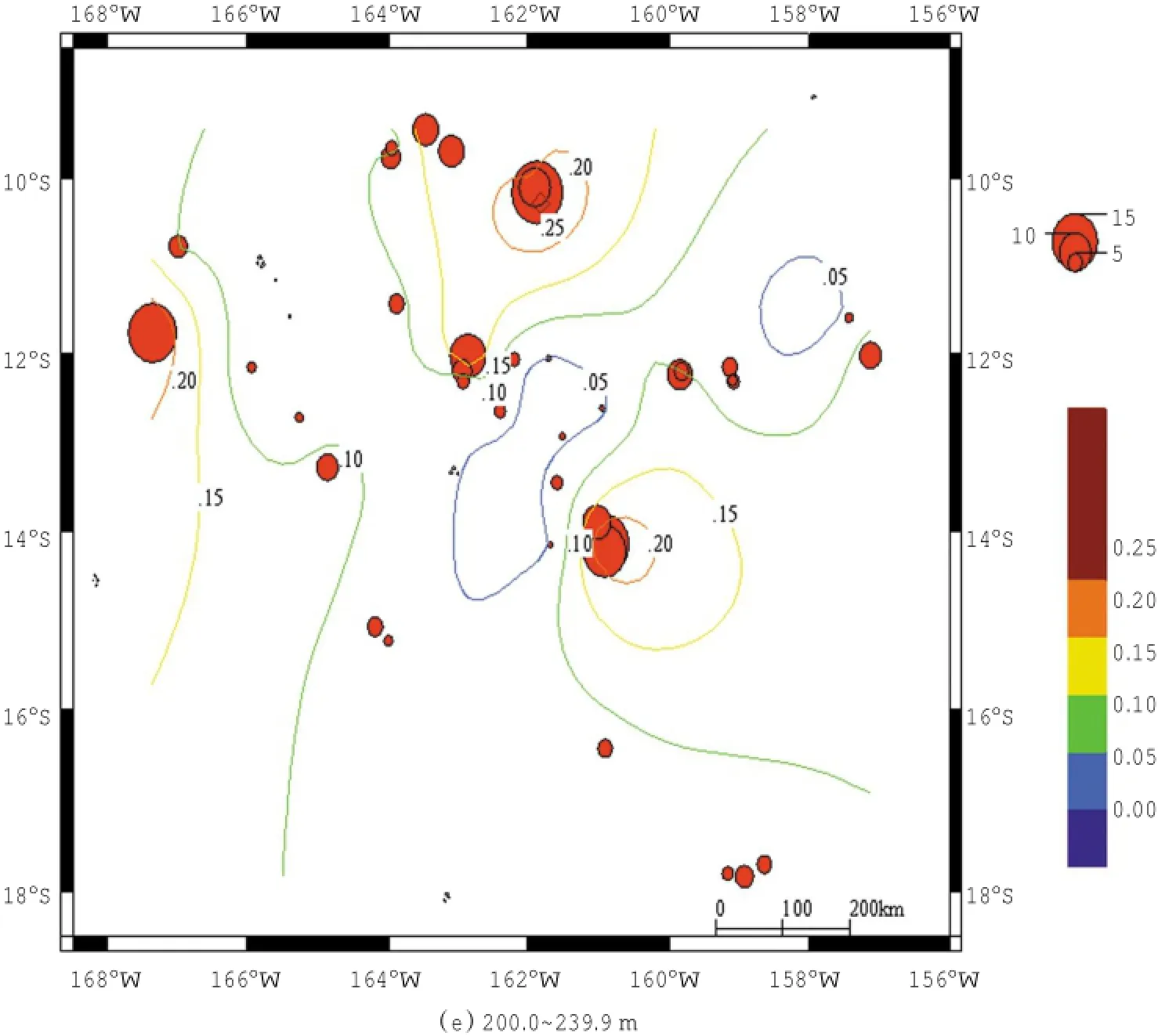
圖3 庫克群島海域不同水層長鰭金槍魚IHIij分布與名義CPUE

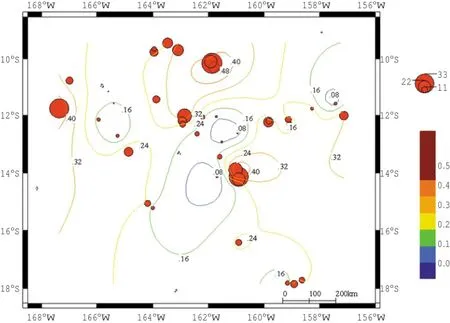
圖4 庫克群島海域長鰭金槍魚IHIi和名義CPUE分布

2.3 IHI模型的驗證

將各水層和整個水體內(nèi)用于模型驗證站點的環(huán)境數(shù)據(jù)輸入到各相應的長鰭金槍魚CPUE預測模型，得到各驗證站點各個水層及整個水體長鰭金槍魚的預測CPUE（圖5），使用Wilcoxon檢驗方法檢驗驗證站點名義CPUE與預測CPUE間是否存在

顯著性差異，結(jié)果見表3，所有水層及整個水體的預測CPUE與名義CPUE均無顯著性差異（P> 0.05）。驗證站點內(nèi)不同水層IHIij預測值的算術(shù)平均值IHIj與各水層長鰭金槍魚名義CPUE的算術(shù)平均值CPUEj的比較見圖6，兩者間的Spearman相關系數(shù)達到0.99。

表2 庫克群島海域相對較高的IHIij和IHIi的海區(qū)范圍及其對應的IHI值

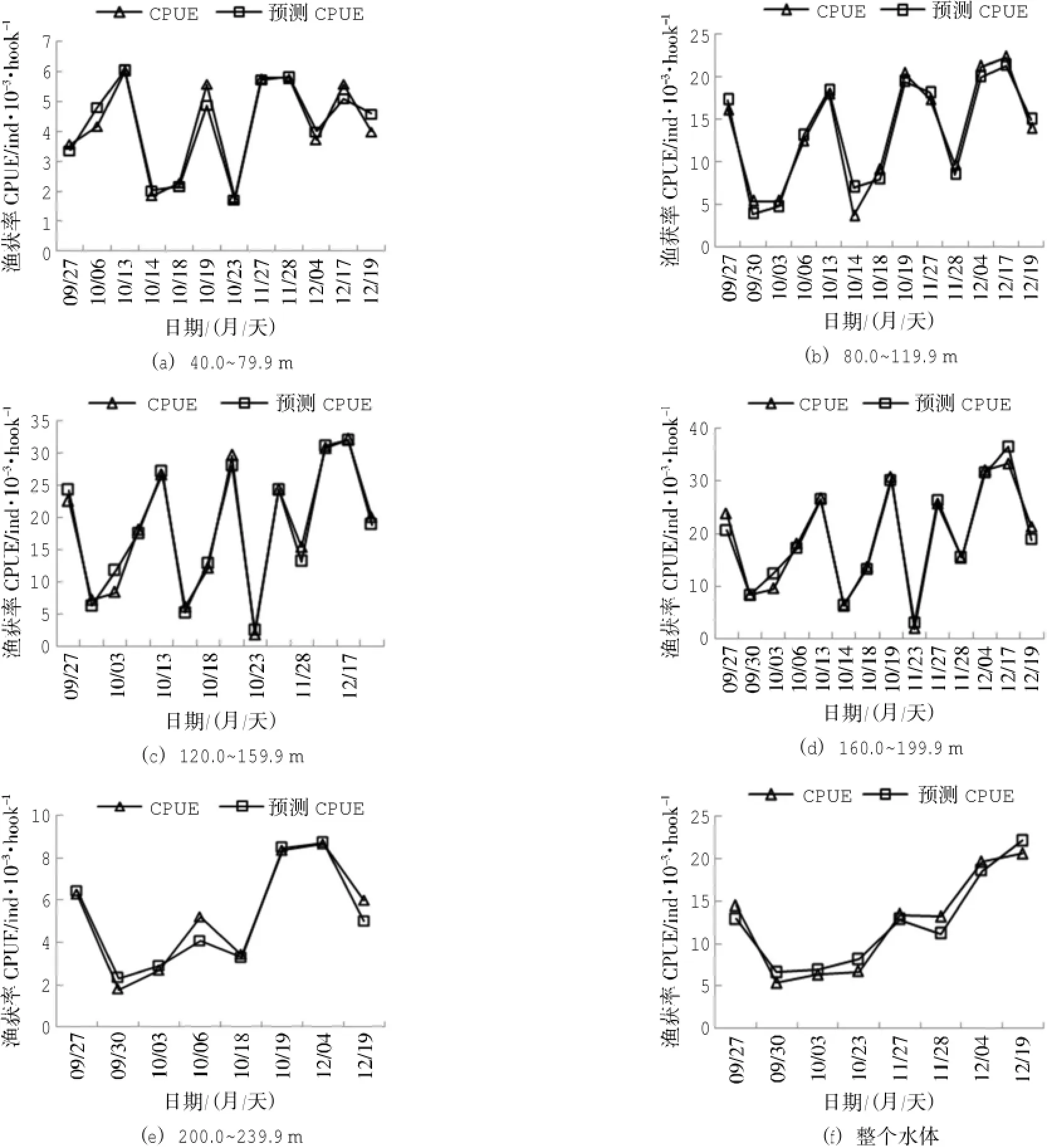
圖5 驗證站點長鰭金槍魚名義CPUE與預測CPUE

表3 名義CPUE與預測模型預測CPUE的符號秩檢驗結(jié)果

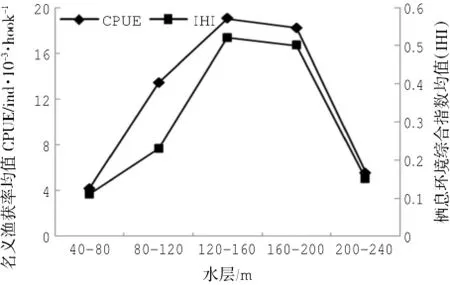
圖6 驗證站點內(nèi)各水層預測的IHI均值與對應各水層長鰭金槍魚名義CPUE均值

將42個模型建立站點的長鰭金槍魚預測CPUE輸入到IHI模型,得出各個水層及整個水體的IHI預測值（圖7）,本文采用Spearman相關系數(shù)分析各水層的棲息環(huán)境綜合指數(shù)與其對應的長鰭金槍魚實測CPUE之間的關系，檢驗標準設定為：相關系數(shù)小于0.4時為差；0.4~0.49為中；0.5~0.69為良；大于0.7為優(yōu)（楊嘉樑等，2014）。并基于這一標準評價模型預測長鰭金槍魚CPUE分布的能力，各水層預測能力見表4，其中預測能力最佳的水層為40.0~79.9 m和200.0~239.9 m，預測能力為優(yōu)。不同水層IHIij預測值的算術(shù)平均值IHIj與各水層長鰭金槍魚名義CPUE的算術(shù)平均值CPUEj的比較見圖8，兩者間的Spearman相關系數(shù)達到0.99。

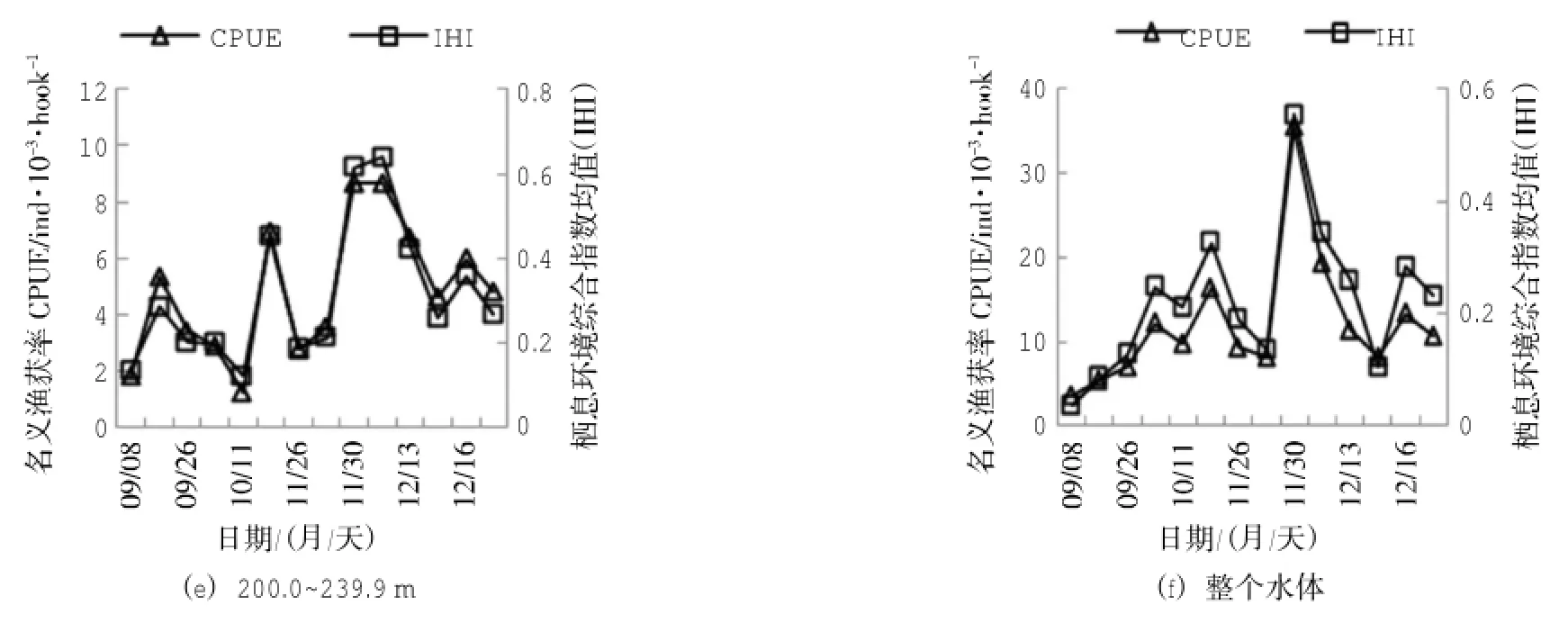
圖7 建模站點長鰭金槍魚名義CPUE與IHI預測值

表4 建模站點內(nèi)各水層預測的IHI指數(shù)與名義CPUE間的Spearman相關系數(shù)及預測能力

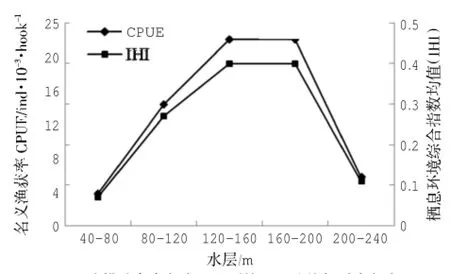
圖8 建模站點內(nèi)各水層預測的IHI均值與對應各水層長鰭金槍魚名義CPUE均值

3 討論

3.1選擇支持向量機方法用于本研究的依據(jù)

本研究總樣本數(shù)較少，傳統(tǒng)的線性模型對輸入數(shù)據(jù)存在一定的限制，支持向量機方法是專門針對小樣本學習問題提出的，而且采用二次規(guī)劃尋優(yōu)（Bottou et al，2011），因此可以得到全局最優(yōu)化。傳統(tǒng)線性模型數(shù)據(jù)需滿足正態(tài)分布，但是從圖9可以看出各水層樣本數(shù)據(jù)并不滿足正態(tài)分布，而支持向量機采用核函數(shù)使得算法的復雜度與樣本維數(shù)無關，非常適合處理非線性問題，另外支持向量機應用結(jié)構(gòu)風險最小化原則，因而支持向量機具有非常好的推理能力，這就使得選用站點數(shù)據(jù)的準確度很高，更利于模型的預測（Hsieh et al，2009）。

3.2部分水層模型預測能力較差的原因

雖然各個水層及整個水體內(nèi)預測CPUE與名義CPUE間的P值均大于0.05（表3），但部分水層，如在80.0~119.9 m水層內(nèi)，預測CPUE與名義CPUE間的Spearman相關系數(shù)值較低（表4），僅為0.34，主要原因是由于本研究各水層的環(huán)境數(shù)據(jù)采用了計算各相應水層環(huán)境數(shù)據(jù)的算術(shù)平均值而得出。80.0~119.9 m水層處在混合層的下部與溫躍層上界所在的水層（見圖2），所以溫度變化幅度較大，而且80.0~119.9 m水層預測模型中溫度的系數(shù)最大（0.64，見表1）所以模型結(jié)果會受到影響。這與楊嘉樑等（2014）用分位數(shù)回歸的方法得出80.0~119.9 m水層內(nèi)長鰭金槍魚分布預測模型的預測能力較差相一致。

在160.0~199.9 m水層內(nèi)，預測CPUE與名義CPUE間的Spearman相關系數(shù)值僅為0.45（表4）。該水層的CPUE預測模型的自變量為溫度、葉綠素a濃度、垂直海流及水平海流，其中，葉綠素a濃度的系數(shù)高達0.92，溫度的系數(shù)值為0.63，遠高于垂直海流及水平海流的系數(shù)（見表1）；由圖2可知160.0~199.9 m水層葉綠素a濃度處于由大變小的躍層，而且不同的站位變化的幅度較大，由于本研究采用了各水層環(huán)境數(shù)據(jù)的算術(shù)平均值代表該水層的環(huán)境因子值，因此，導致該水層CPUE模型的預測效果受到影響。

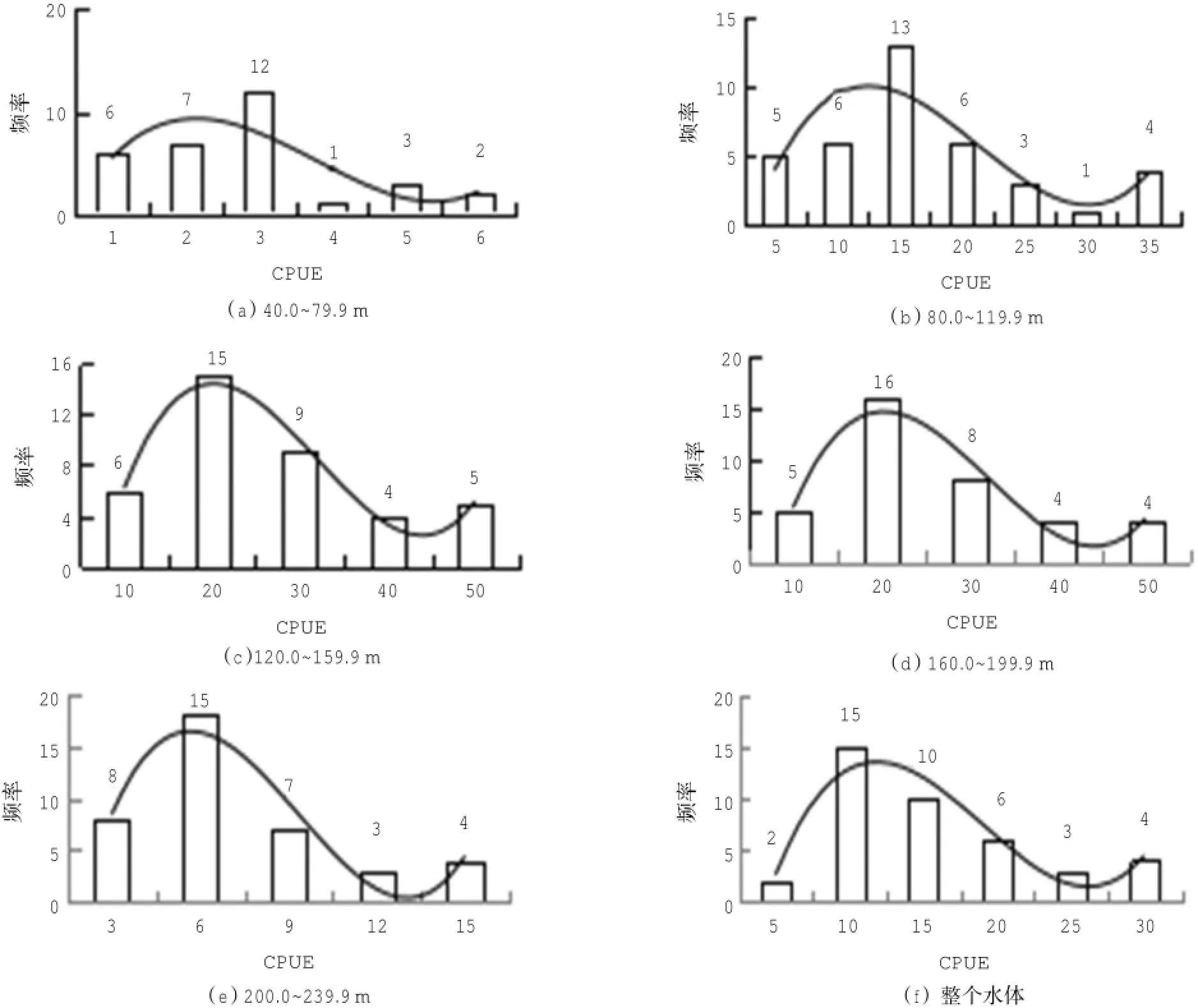
圖9 不同水層及整個水體長鰭金槍魚名義CPUE的出現(xiàn)頻率

3.3 IHI模型的有效性及預測能力的評價

通過將驗證站點的各水層及整個水體的環(huán)境數(shù)據(jù)輸入對應水層的長鰭金槍魚CPUE預測模型所得結(jié)果與名義CPUE比較發(fā)現(xiàn)（表3、圖6）：所有水層長鰭金槍魚的預測CPUE與名義CPUE之間均無顯著性差異（P>0.05）。由圖6可知，驗證站點各水層長鰭金槍魚名義CPUE的算術(shù)平均值與其對應IHI預測指數(shù)的算術(shù)平均值的變化趨勢總體相同。綜上所述，IHI模型可以用于預測庫克群島海域各水層及整個水體的IHI指數(shù)。

(一)要在學習培訓上下功夫，需要行政事業(yè)單位加強對會計工作人員的系統(tǒng)培訓，提高會計工作人員的從業(yè)水平，讓相關的工作人員真正學懂學精政府會計制度和相關準則，并能根據(jù)其變化，不斷完善自身，從而滿足財務工作的需要，在工作崗位上做出自己所能做出的貢獻。

通過表4可以看出，除80.0~119.9 m水層外，IHI模型預測長鰭金槍魚分布的能力總體屬于優(yōu)良，由圖8可知，各水層長鰭金槍魚名義CPUE的算術(shù)平均值與其對應IHI預測指數(shù)的算術(shù)平均值的變化趨勢總體相同，兩者間的Spearman相關系數(shù)也高達0.99。其中，120.0~159.9 m、160.0~199.9 m水層長鰭金槍魚名義CPUE算術(shù)平均值、IHI預測指數(shù)的算術(shù)平均值均為最高，分別為23尾/1000鉤和0.4左右，因此可以判斷在庫克群島海域，長鰭金槍魚主要棲息的水層為120.0~199.9 m。該水層對應的溫度范圍為19.6℃~25.2℃（圖2），處在戴芳群等（2006）研究認為中東太平洋長鰭金槍魚棲息水溫為13.5℃~25.2℃的范圍內(nèi)，與楊嘉樑等（2014）和宋利明等（2016）研究得出的長鰭金槍魚較為適宜的棲息水溫為20.0℃~25.0℃和21.0℃~ 23.9℃基本一致。Hazen et al（2013）研究得出長鰭金槍魚偏好的水溫為20.0℃以上。本研究得出的長鰭金槍魚的主要分布水層比所羅門群島海域的（130~160 m）略深（林顯鵬等，2011）。此外，120.0~159.9 m水層葉綠素濃度為0.07~0.49 μg/L，與Lezama-Ochoa等（2010）認為長鰭金槍魚棲息適宜葉綠素濃度為0.4~0.8 μg/L差異較大。這些可能是由于調(diào)查海域的不同所造成的。

3.4影響長鰭金槍魚分布的主要環(huán)境因子

不同水層影響長鰭金槍魚分布的主要因素不同，在40.0~79.9 m、80.0~119.9 m、120.0~159.9 m、160.0~199.9 m和200.0~239.9 m水層其分布分別主要受葉綠素a濃度、水溫、垂直海流、葉綠素a濃度和溫度的影響。整個水體影響長鰭金槍魚分布的主要因素為溫度。這與楊嘉樑等（2014）得出的各水層影響長鰭金槍魚分布的主要環(huán)境因子相一致,庫克群島海域長鰭金槍魚在較淺水域的分布模式主要受水色及溫度的影響，在120.0~159.9 m水層則受海流的影響較大，而在較深的水層其分布則主要受餌料分布及溫度的限制。由于長鰭金槍魚的心臟位于逆流熱交換器的外側(cè)，能夠立刻感受外部溫度的變化（Galli et al，2011），溫度控制其心臟功能和垂直移到模式（Horodysky et al，2016）。因此，溫度成為影響長鰭金槍魚在整個水體中分布的主要因素，這與Briand等（2011）和Arrizabalaga等（2014）的觀點一致。

3.5提高目標魚種漁獲率并減少兼捕率的建議

對于庫克群島海域，長鰭金槍魚IHIi和指數(shù)較高的海域為9°00′S-12°20′S，159°00′W-164°00′W、13°30′S-14°30′S，159°00′W-161°00′W和10°30′S-12°30′S，167°00′W-168°00′W（表2）。在該3個海域作業(yè)時為了提高長鰭金槍魚的漁獲率并減少其他保護物種的兼捕率，建議盡可能使延繩釣釣鉤投放至120.0~159.9 m的水層。

3.6本研究的不足及展望

本文只將溫度、葉綠素a濃度、水平海流和垂直海流用于長鰭金槍魚棲息環(huán)境綜合指數(shù)的研究，還需要進一步研究判斷鹽度、溶解氧等其他因子對長鰭金槍魚分布的影響程度。在今后的研究中，還應盡量增加每個站點各水層的釣鉤數(shù)，同時增加站點數(shù)量，以便提高預測庫克群島海域長鰭金槍魚分布模型的精度。

致謝：本研究得到了庫克群島政府的許可，并得到深圳市華南漁業(yè)有限公司董事長黃富雄、“華南漁719”號船長及全體船員等大力支持，謹致謝意。

Arrizabalaga H,Dufour F,Kell L,et al,2015.Global habitat preferences of commercially valuable tuna.Deep-Sea Research.II:Topical Studies in Oceanography,113:102-112.

Bottou L,Giles C L.2011.Nonconvex online support vector machines. Pattern Analysis and Machine Intelligence,IEEE Transactions,33 (2):368-381.

Briand K,Molony B,Lehodey P,2011.A study on the variability of albacore(Thunnus alalunga)longline catch rates in the southwest Pacific Ocean.Fisheries Oceanography,20(6):517-529.

Cortes C,Vapnik V,1995.Support-vector networks.Machine Learning, 20(3):273-297.

Galli G L J,Lipnick M S,Shiels H A,et al,2011.Temperature effects on Ca2+cycling in scombrid cardiomyocytes:a phylogenetic comparison. Journal of Experimental Biology,214:1068-1076.

Harrell F E,Lee K L,Mark D B,1996.Tutorial in biostatistics multivariable prognostic models:issues in developing models,evaluating assumptions and adequacy,and measuring and reducing errors.Statistics in Medicine,1(15):361-387.

Hazen E L,Jorgensen S,Rykaczewski R R,et al,2013.Predicted habitat shifts of Pacific top predators in a changing climate.Nature Climate Change,3(3):234-238.

Hinton M G,Maunder M N,2004.Methods for standardizing CPUE and how to select among them.Col.Vol.Sci.Pap.ICCAT,56(1):169-177.

Horodysky A Z,Cooke S J,Graves J E,et al,2016.Fisheries conservation on the high seas:linking conservation physiology and fisheries ecology for the management of large pelagic fishes.Conservation Physiology,4:doi:10.1093/conphys/cov059.

Howell E A,Hawn D R,Polovina J,2010.Spatiotemporal variability in bigeye tuna(Thunnus obesus)dive behavior in the central North Pacific Ocean.Progress in Oceanography,86(1):81-93.

Hoyle S D,Davies N,2009.Stock assessment of albacore tuna in the south PacificOcean.ScientificCommitteeFifthRegularSession. WCPFC-SC5-2009/SAWP-6,Vanuatu,10-21 August.

Hsieh T W,Taur J S,Tao C W,et al.2009.A kernel-based core growing clustering method.International Journal of Intelligent Systems,12 (4):441-458.

Laurs M R,Fiedler P C,Montgomery D R,1984.Albacore tuna catch distributions relative to environmental features observed from satellites. Deep Sea Research Part A.Oceanographic Research Papers,31 (9):1085-1099.

Lezama-Ochoa A,Boyra G,Go?i N,et al.2010.Investigating relationships between albacore tuna(Thunnus alalunga)CPUE and prey distribution in the Bay of Biscay.Progress in Oceanography,39 (1):105-114.

Maunder M N,Punt A E,2004.Standardizing catch and effort data:a review of recent approaches.Fisheries Research,70(2):141-159.

Murray T,1994.A review of the biology and fisheries for albacore,Thunnus alalunga,in the South Pacific Ocean.FAO Fisheries Technical Paper(FAO).

Okamoto H,2008.Japanese longline CPUE for bigeye tuna standardizedfor two area definitions in the Atlantic Ocean from 1961 up to 2005. Collect.Vol.Sci.Pap.ICCAT,67(2):419-439.

Olds E G,1949.The 5%significance levels for sums of squares of rank differences and a correction.The Annals of Mathematical Statistics, 20(1):117-118.

Roberts P E,1980.Surface distribution of albacore tuna,Thunnus alalunga Bonnaterre,in relation to the Subtropical Convergence Zone east of New Zealand.New Zealand Journal of Marine and Freshwater Research,14(4):373-380.

Song L M,Wu Y P,2011.Standardizing CPUE of yellowfin tuna(Thunnus albacares)longline fishery in the tropical waters of the northwestern Indian Ocean using a deterministic habitat-based model. Journal of Oceanography,67(5):541-550.

Su N J,Yeh S Z,Sun C L,et al,2008.Standardizing catch and effort data of the Taiwanese distant-water longline fishery in the western and central Pacific Ocean for bigeye tuna,Thunnus obesus.Fisheries Research,90(1):235-246.

Wang C H,Wang S B,2006.Assessment of South Pacific albacore stock (Thunnus alalunga)by improved Schaefer model.Journal of Ocean University of China,5(2):106-114.

Wilcoxon F,1945.Individual comparisons by ranking methods.Biometrics Bulletin,12(1):80-83.

Wu G C,Chiang H C,Chen K S,et al.2009.Population structure of albacore(Thunnus alalunga)in the Northwestern Pacific Ocean inferred from mitochondrial DNA.Fisheries Research,95(1):125-131.

Zainuddin M,Kiyofuji H,Saitoh K,et al.2006.Using multi-sensor satellite remote sensing and catch data to detect ocean hot spots for albacore(Thunnus alalunga)in the northwestern North Pacific.Deep Sea Research Part II:Topical Studies in Oceanography,53(3): 419-431.

Zainuddin M,Saitoh K,Saitoh S I,2008.Albacore(Thunnus alalunga) fishing ground in relation to oceanographic conditions in the western North Pacific Ocean using remotely sensed satellite data.Fisheries Oceanography,17(2):61-73.

Zainuddin M,Saitoh S I,et al.2004.Detection of potential fishing ground for albacore tuna using synoptic measurements of ocean color and thermal remote sensing in the northwestern North Pacific.Geophysical Research Letters,31(20):1-4.

陳錦淘，戴小杰，谷兵，2005.中國南太平洋長鰭金槍漁業(yè)發(fā)展對策的分析.中國漁業(yè)經(jīng)濟，1（2）：49-50，55.

陳雪忠，樊偉，崔雪森，等，2013.基于隨機森林的印度洋長鰭金槍魚漁場預報.海洋學報（中文版），35（1）：158-164.

戴芳群，李顯森，王鳳臣，等，2006.中東太平洋長鰭金槍魚延繩釣作業(yè)分析.海洋水產(chǎn)研究，27（06）：37-42.

樊偉，張晶，周為峰，2007.南太平洋長鰭金槍魚延繩釣漁場與海水表層溫度的關系分析.大連水產(chǎn)學院學報，22（5）：366-371.

范江濤，陳新軍，錢衛(wèi)國，等，2011.南太平洋長鰭金槍魚漁場預報模型研究.廣東海洋大學學報，31（6）：61-67.

林顯鵬，郭愛，張洪亮，等，2011.所羅門群島海域長鰭金槍魚的垂直分布與環(huán)境因子的關系.浙江海洋學院學報（自然科學版），30（4）：303-306.

宋利明，謝凱，趙海龍，等，2017.庫克群島海域海洋環(huán)境因子對長鰭金槍魚漁獲率的影響.海洋通報，36（1）：96-106.

宋利明，楊嘉樑，胡振新，等，2011.兩種延繩釣釣具大眼金槍魚捕撈效率的比較.上海海洋大學學報，20（3）：424-430.

宋利明，楊嘉樑，武亞蘋，等，2012.吉爾伯特群島海域大眼金槍魚（Thunnus obesus）棲息環(huán)境綜合指數(shù).海洋與湖沼，43（5）：954-962.

楊嘉樑，黃洪亮，宋利明，等，2014.基于分位數(shù)回歸的庫克群島海域長鰭金槍魚棲息環(huán)境綜合指數(shù).中國水產(chǎn)科學，21（4）：832-851.

袁紅春，湯鴻益，陳新軍，2010.一種獲取漁場知識的數(shù)據(jù)挖掘模型及知識表示方法研究.計算機應用研究，27（12）：4443-4446.

齋藤昭二，1992.マグロの游泳層と延繩漁法.東京：成山堂書屋：19-63.

張浩然，韓正之，李昌剛，2002.支持向量機.計算機科學，29（12）：135-137，142.

張利田，卜慶杰，楊桂華，等，2007.環(huán)境科學領域?qū)W術(shù)論文中常用數(shù)理統(tǒng)計方法的正確使用問題.環(huán)境科學學報，27（1）：171-173.

周甦芳，樊偉，2006.太平洋延繩釣長鰭金槍魚及漁場水溫分析.海洋湖沼通報，6（2）：38-43.

（本文編輯：袁澤軼）

An integrated habitat index for albacore tuna（Thunnus alalunga）in waters near Cook Islands based on the support vector machine method

SONG Li-ming1,2,3,4,ZHOU Jian-kun1,SHEN Zhi-bin1,ZHAO Hai-long1,XIE Kai1
（1.College of Marine Sciences,Shanghai Ocean University,Shanghai 201306,China;2.National Engineering Research Center for Oceanic Fisheries,Shanghai 201306,China;3.Key Laboratory of SustainableExploitation of Oceanic Fisheries Resources（Shanghai Ocean University）,Ministryof Education,Shanghai 201306,China; 4.CollaborativeInnovation Center for Distant-water Fisheries,Shanghai 201306,China）

It will be beneficial to the sustainable utilization of albacore tuna(Thunnus alalunga)resources to better understand the integrated influence of the environmental variables on its distribution.The catch rates and environmental variables(temperature,chlorophyll-a,horizontal current,vertical current)were collected from 56 sampling stations in waters near Cook Islands from Sep,2013 to Dec,2013.The relationships between the catch rate of albacore tuna and the environmental variables were analyzed and the models were developed to estimate integrated habitat indices(IHI)for albacore tuna at five depth strata(40 m each)and the entire water column between 40m and 240 m,and to predict the spatial distributions of albacore tuna in these depths.The support vector machine(SVM)method was used to develop the IHI models.These IHI models were verified by using the data collected at 14 verification stations.Results showed that:(1)there was no significant difference between the nominal catch rates and the predicted catch rates;(2)The IHI models developed in this study performed well in predicting catch rate distribution of albacore tuna with selected environmental variables;(3)The key environmental parameters in the IHI models differed among the depth strata.The chlorophyll-a concentration,water temperature,vertical current,chlorophyll-a concentration and water temperature were the key variables that influenced the albacore tuna distribution at the depth strata of 40.0~79.9m,80.0~119.9m,120.0~159.9m,160.0~199.9m and 200.0~239.9m,respectively.The temperature was the key variable that influenced the albacore tuna distribution at the entire water column;(4)The preferred swimming depth stratum of albacore tuna was 120.0~199.9m;(5)The IHIs for albacore tuna in the areas at 9°00′S-12°20′S,159°00′W-164°00′W；13°30′S-14°30′S, 159°00′W-161°00′W and 10°30′S-12°30′S,167°00′W-168°00′W were relatively high.Results suggested to deploy the longlines at the water depth of 120~199.9 m to improve the catch rate of albacore tuna and reduce the by catch rate when fishing in these areas.

albacore tuna;integrated habitat index;support vector machine(SVM);Cook Islands

P73.5

A

1001-6932（2017）02-0195-12

10.11840/j.issn.1001-6392.2017.02.011

2015-12-08；

2016-02-25

國家高技術(shù)研究發(fā)展計劃（2012AA092302）；高等學校博士學科點專項科研基金聯(lián)合項目（20113104110004）；上海市教育委員會科研創(chuàng)新項目（12ZZ168）；農(nóng)業(yè)部遠洋漁業(yè)資源探捕項目（D8006128005）。

宋利明，博士生導師，教授，主要從事金槍魚漁業(yè)和漁具數(shù)值模擬研究。電子郵箱：lmsong@shou.edu.cn。