齒輪箱殼體及軸承支撐剛度對風電機組傳動鏈固有頻率的影響*

文 | 張靜，姜少輝，盛秋剛，董振華

技術

齒輪箱殼體及軸承支撐剛度對風電機組傳動鏈固有頻率的影響*

文 | 張靜，姜少輝，盛秋剛，董振華

近幾十年，隨著石油、天然氣等能源的枯竭以及人們對于環境問題的日益重視，全球風電總裝量不斷擴增，根據世界風能協會掌握的數據，到2020年全球風電容量將接近239GW，足夠滿足世界3%的用電。我國從2003年以來裝機容量快速增長，到2010年底我國風電裝機容量已經躍居世界第一，成為全球風電裝機速度最快的國家。

風電機組按照傳動形式可劃分為：多級齒輪傳動型、半直驅型和直驅型三大類。大部分制造商采用了雙饋感應發電機以及多級增速齒輪箱的機組類型，如Vestas，Gamesa，GE wind，REpower。這種風電機組傳動鏈包括葉片、輪轂、主軸（主軸承）、齒輪箱、減震裝置、聯軸器、發電機等。由于風電機組傳動鏈系統的工作轉速范圍廣，激勵頻率帶較寬，在時變外部載荷和內部載荷的共同作用下易與系統發生共振，造成整個風電機組的失效和重大安全事故，因此風電機組傳動鏈系統的動態特性研究對于兆瓦級風電機組的高可靠運行有著十分重要的意義。

國內風電機組傳動鏈的研究相對國外較為滯后，2005年朱才朝等人建立了風電機組多級齒輪傳動的齒輪—傳動軸—箱體的耦合非線性動力學模型，對風電機組傳動鏈中的齒輪傳動系統進行動態特性分析。2009年顧僉利用多體動力學軟件SIMPACK建立了兩級行星一級平行軸的風電機組傳動鏈動力學模型，結合坎貝爾圖和能量圖頻率分析，并通過掃略計算，對轉動方向內的固有頻率一一進行排除，較為完整地進行了傳動鏈的共振分析。

傳動鏈的拓撲建模

在既往的風電機組傳動鏈共振分析中，軸類零件、葉片、行星架按照柔性體設置，輪轂、行星架、齒輪箱外殼、主機架、聯軸器、發電機支架、主機架均按照剛體設置， 其中輪轂采用有限元軟件計算其旋轉剛度，并通過FE13施加，聯軸器（包括剎車盤）分成四段，每段之間的扭轉剛度由廠家提供。在GL規范2010版中，針對傳動鏈建模做出了更為詳細的規定，見表1。

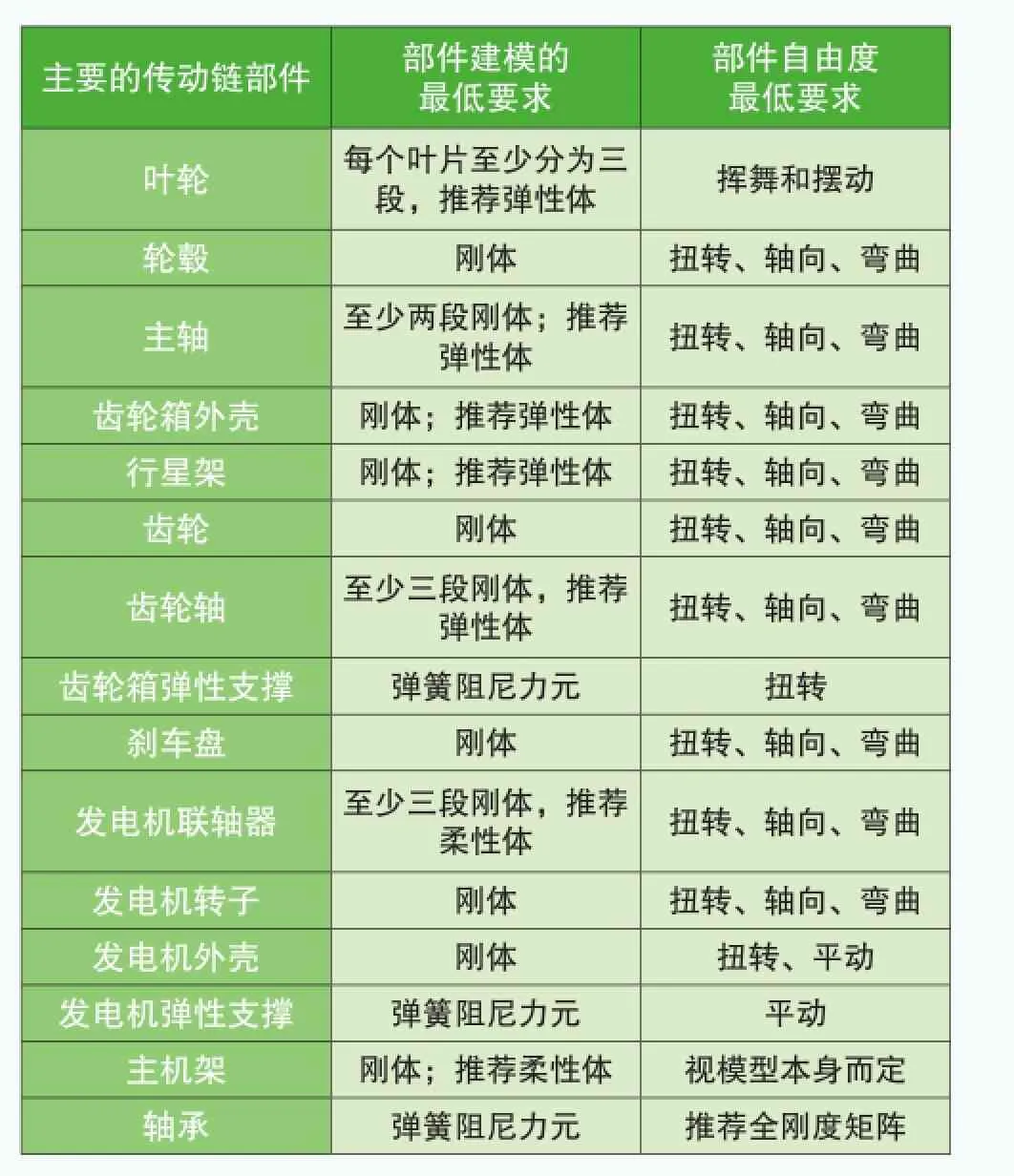
表1 主要傳動鏈部件的建模要求

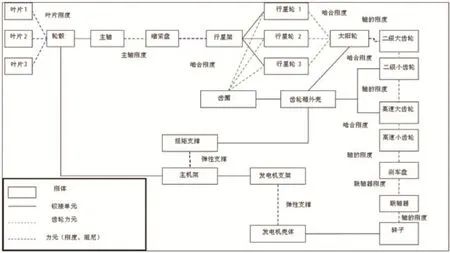
圖1 傳動鏈拓撲關系

圖2 主節點的設置（前面）

圖3 主節點的設置（后面）

由表1可得，軸類零件、行星架、齒輪箱外殼、主機架推薦柔性體，軸承推薦6×6階剛度矩陣。柔性體越多，計算時間越長，因此在保證結果正確性的前提下，應該盡量減少柔性體的個數。同時齒輪箱內的軸承矩陣往往很難從供應商處獲得，因此承受徑向力的圓柱滾子軸承常采用93號力元來模擬軸承支撐剛度。本文建立了三點支撐傳動鏈模型，拓撲關系見圖1，對比了齒輪箱外殼為剛體和柔性體下，傳動鏈旋轉面內固有頻率的變化；同時對比了齒輪箱內軸承支撐剛度對傳動鏈轉動平面內固有頻率的影響，完成齒輪箱部分參數的敏感性分析，對風電機組傳動鏈共振分析有一定的指導意義。

齒輪箱外殼的柔性化

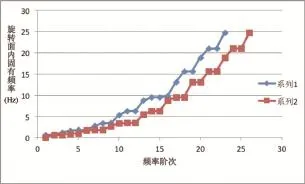
圖4 剛、柔齒輪箱傳動鏈固有頻率對比（30Hz以內）

圖6 剛、柔齒輪箱傳動鏈固有頻率對比（30Hz之外）

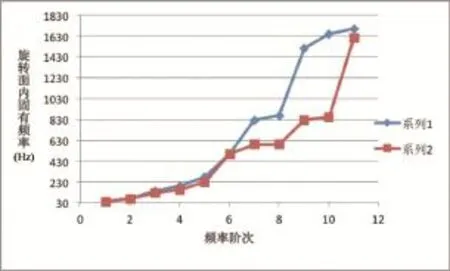
圖5 不同軸承剛度傳動鏈固有頻率對比（30Hz以內）

圖7 不同軸承剛度傳動鏈固有率對頻比（30Hz之外）

為了對比柔性齒輪箱對傳動鏈固有頻率的影響，分別將齒輪箱外殼設置為剛體和柔性體。在Ansys軟件中，采用子結構分析的方法，將所有單元凝結于幾個超單元，得到單元的質量矩陣和剛度矩陣，將fle.sub和fle.cdb文件導入SIMPACK軟件中進行柔性化，得到fle.fbi文件。

圖2和3給出了齒輪箱外殼主節點的設置位置，分別為和齒輪軸的連接軸承處和行星架的連接軸承處，和主機架接觸的彈性支撐處。

齒輪箱外殼剛度和軸承支撐剛度對風電機組頻率的影響

一、剛性和柔性齒輪箱外殼對應的風電機組轉頻

按照圖1對應的拓撲關系，搭建傳動鏈模型，其中軸類零件、葉片、行星架按照柔性體設置，其余零件按照剛體設置。在比較分析時，齒輪箱內軸承支撐剛度設置為1E12N/m。根據GL2010傳動鏈共振分析需要三個狀態：切入、額定、切出，由于三種狀態下風電機組傳動鏈頻率差別很微小，因此選取額定風速為分析條件。輪轂中心輸入額定扭矩，轉子與定子之間輸入發電機功率曲線，進行動平衡計算，直到風電機組達到平衡狀態。保持平衡狀態，進行模態分析，結合陣型和各個部件的能量圖得到傳動鏈轉動平面內固有頻率。圖4、圖5給出了剛性齒輪箱殼體和柔性齒輪箱殼體傳動鏈轉動平面內固有頻率。

其中系列1代表齒輪箱外殼為剛體時，傳動鏈轉動平面內固有頻率，系列2代表齒輪箱外殼為柔性體時，傳動鏈轉動平面內固有頻率。

二、不同軸承支撐剛度對應的風電機組轉頻

齒輪箱外殼設置為剛體，分別計算了齒輪箱內軸承支撐剛度為1E12 N/m、1E10 N/m、1E8 N/m時，傳動鏈的轉動平面內的固有頻率，見圖6、圖7。

其中系列1代表軸承剛度為1E12 N/m時傳動鏈轉動平面內固有頻率，系列2代表軸承剛度為1E10N/m時傳動鏈轉動平面內固有頻率，系列3代表軸承剛度為1E8 N/m時傳動鏈轉動平面內固有頻率。

結論

從圖4可以看到5Hz－30Hz，柔性殼體和剛性殼體的頻率差別很小，相近頻率的對比，最大差別是0.4%。5Hz以內，柔性殼體的固有頻率為12階，剛性殼體的固有頻率為9階，多出的頻率分別為0.051Hz、0.872Hz、0.995Hz。從圖4、圖5可以看出30Hz以上的頻率，前兩階基本吻合，后續頻率的差別比較大，柔性殼體的頻率偏小，并且高階頻率個數偏少。綜上可知，由于30Hz以內的頻率主要代表葉片的轉動頻率，因此齒輪箱的剛度對此范圍內的頻率影響不大；30Hz以外的頻率，代表傳動鏈其他部件的頻率，齒輪箱的剛度對此范圍內的頻率影響較大。所以柔性殼體雖然會延長計算時間，但是計算結果和剛性殼體有明顯的差別，建議采用柔性殼體參與計算。

從圖6可以得出30Hz以內，支撐剛度的變化對頻率的影響非常微小，很多階次甚至數據完全吻合，這也恰恰表明齒輪箱內的參數變化對葉片固有頻率是基本沒有影響的。從圖7可以看出，軸承支撐剛度為1E12 N/m和1E10 N/m時，頻率的差別微小，相近頻率的偏差僅為0.005%，只有在高頻處，前者多出一階頻率；當軸承支撐剛度為1E8 N/m時，頻率與前兩者部分吻合，低階和高階頻率差別較大。所以齒輪箱內軸承的支撐剛度對傳動鏈的固有頻率有一定的影響，當軸承剛度越來越大時，傳動鏈固有頻率變化不大；當軸承剛度變小時，頻率變化明顯。建議采用6×6階矩陣來表達軸承剛度，從而得到準確的計算結果。

（作者單位：張靜，姜少輝，董振華：華銳風電科技（集團）股份有限公司；盛秋剛：上海綠色環保能源有限公司）

攝影：李志明

上海市科學技術委員會項目“深遠海上風電機組設計開發及運維相關技術研究”（項目（課題）編號：16DZ1203505）