具有階段結構的周期SEIR傳染病模型的動力學性態

杜燕飛, 肖 鵬, 曹 慧

(陜西科技大學 數學系, 陜西 西安 710021)

具有階段結構的周期SEIR傳染病模型的動力學性態

杜燕飛, 肖 鵬, 曹 慧

(陜西科技大學 數學系, 陜西 西安 710021)

假設總人口分為幼年和成年2個階段,且只有成年個體染病,建立一類具有階段結構的周期SEIR傳染病模型,得到無病周期解全局穩定性的條件;進一步討論模型的一致持續生存,并用數值模擬驗證所得到的結論.

周期傳染病模型； 階段結構； 基本再生數； 穩定性

近年來,通過傳染病模型研究傳染病動力學受到廣泛關注.在傳染病的研究過程中,人們發現很多疾病只在某個特定的年齡階段傳播,如麻疹、水痘等傳染病多發于幼年階段,而性病、傷寒、血吸蟲病、白喉等傳染病多傳播于成年階段[1-4].另一方面,人類的活動會受到季節和氣候影響,導致很多疾病的傳染和爆發也隨季節顯示出周期性波動[5-9].因此,在刻畫傳染病模型時,考慮具有階段結構的并且具有周期系數的模型能更好地描述這類疾病的傳播特點,更具有現實意義.本文將建立一類具有階段結構的周期SEIR傳染病模型,并研究其動力學性態.

假設總人口分為幼年、成年2個階段,且只有成年個體感染此病,構建系統(1).

(1)

其中,用X(t)表示t時刻幼年個體的數量,并將成年個體分為4類:易感者S(t)、潛伏者E(t)、染病者I(t)和恢復者R(t).Λ(t)是人口增長率函數,ω(t)為幼年個體到成年個體的轉化率,μ0(t)、μ(t)分別為幼年、成年的自然死亡率,ε(t)和α(t)分別表示潛伏者的發病率和染病者的治愈率,采用非線性發生率β(t)S2(t)I(t),并假設所有的參數函數均為正的ω周期函數.

1 預備知識

首先考慮系統(1)的無病周期解的存在性.考察方程

將系統(1)中所有方程相加得

其中

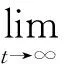
引理 1 系統(1)具有初始條件X(0)>0,S(0)>0,E(0)>0,I(0)>0,R(0)>0的解(X(t),S(t),E(t),I(t),R(t))在[0,+∞)上存在且為有界的正解.

由于模型(1)中的前4個方程中不含R(t),且關于R(t)的方程是線性的,因此只須考慮前4個方程構成的模型,即如下系統(3)的動力學性態.

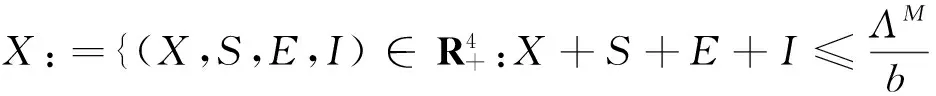
下面利用文獻[10]中積分算子譜半徑的方法來定義系統(3)的基本再生數.首先驗證文獻[10]中的條件(A1)～(A7)成立.記x=(E,I,X,S)T,

(4)

容易看出系統(3)等價于如下系統

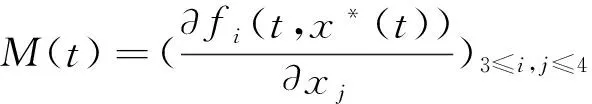
顯然ρ(ΦM(ω))<1,即無病周期解x*(t)=(0,0,X*(t),S*(t))為線性漸近穩定的,于是,文獻[10]中的條件(A6)成立.令

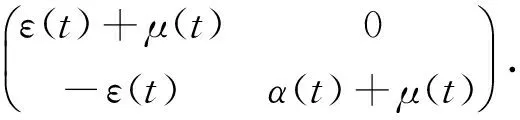
記Y(t,s)是如下系統的一個2×2的矩陣解

其中I是2×2的單位矩陣.顯然文獻[10]中的條件(A7)也成立.

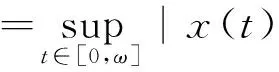
(5)

定義系統(3)的基本再生數為R0=ρ(L),其中ρ表示算子L的譜半徑.

2 主要結果

下面研究系統(3)的全局動力學性態,結果表明基本再生數R0=1是區分疾病一致持續或消除的一個閥值.

定理 1 若R0<1,則無病周期解(X*(t),S*(t),0,0)是全局漸近穩定的；若R0>1，它是不穩定的.

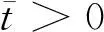
現在考慮如下輔助系統

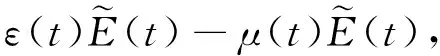
(6)

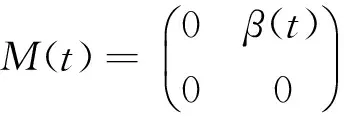
(7)

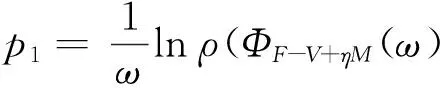
定理 2 如果R0>1,則存在ε>0,使得系統(3)具有初值(X(0),S(0),E(0),I(0))=(X0,S0,E0,I0)∈{(X,S,E,I)∈X:E>0,I>0}的任意解(X(t),S(t),E(t),I(t))滿足

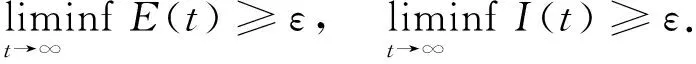
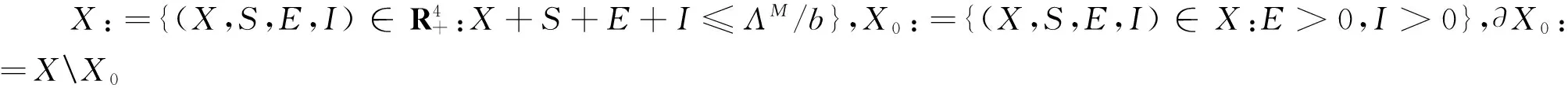
容易證明

(8)

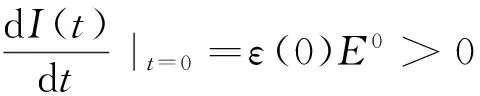
由于R0>1當且僅當ρ(ΦF-V(ω))>1,可選取充分小的η>0,使ρ(ΦF-V+ηM(ω))>1.并考慮系統(3)的擾動系統

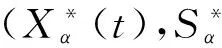
下面證明Ws(M1)∩X0=?.由解對初值的連續依賴性,存在α*>0,使得當‖(X0,S0,E0,I0)-M1‖≤α*時,有

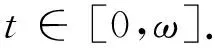
斷言

否則,存在某個(X0,S0,E0,I0)∈X0,使得

不失一般性,假設對任意的m≥0,有

則由解對初值的連續性知,對t∈[0,ω],有

進一步計算可得

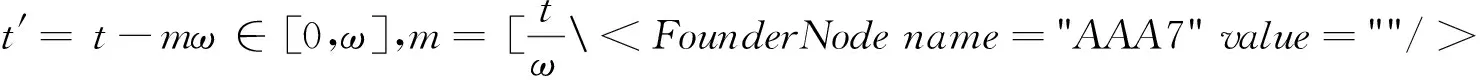
由不等式(10)可推出0≤E(t)≤α,0≤I(t)≤α,t≥0.于是

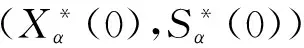
則?t≥T1有:

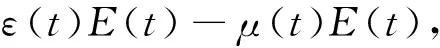
因為ρ(ΦF-V-ηM(ω))>1,由文獻[11]中的引理2.1和標準比較定理可得:

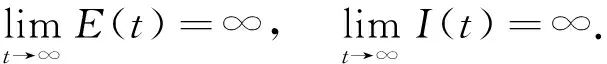
這與0≤E(t)≤α,0≤I(t)≤α矛盾.于是

因為在M?的每一條軌道都收斂于M1,且M1在M?中是非循環的.由一致持續的非循環定理知,P關于(X0,?X0)是一致持續的.又由于M1在X中是孤立的;因此,由文獻[12]中的定理3.1.1知,系統(3)關于(X0,?X0)是一致持續的.

3 比較

下面討論在周期SEIR模型中引入階段結構對基本再生數的影響.考慮系統(3)當接觸率β(t)=β[1+bcos(2πt)]為周期函數,其他參數為正常數的情形.

利用文獻[7]中的近似估計方法,系統(11)的基本再生數

如果忽略階段結構,不分幼年和成年2個階段,那么系統(3)可化為

此時系統的基本再生數

比較系統(11)和(12)的基本再生數,可以得出結論:當研究成人病的傳染病模型時,如果忽略階段結構,將會高估基本再生數;從而高估傳染病的傳播風險.

4 數值模擬

下面，利用數值模擬來驗證所得的結論．對于模型(3),令參數Λ=0.09,ω=0.01,β(t)=2.1[1+0.6cos(2πt)],σ=0.18,μ=μ0=0.07,ε=0.5,α=0.24,則基本再生數R0=0.758<1.在圖1中,模擬了系統(3)具有初始條件X0=0.2,S0=0.2,E0=0.2,I0=0.2的解的漸近性態,表明無病周期解是全局漸近穩定的,傳染病將最終消除.

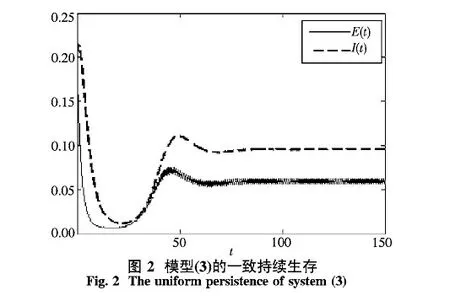
下面取Λ=0.5,其他參數同圖1,則基本再生數R0=2.937>1,圖2的模擬結果說明了系統的一致持續生存.

5 討論

本文將總人口分為幼年和成年2個階段,且假設只有成年個體染病,建立并研究了一類具有階段結構的周期SEIR傳染病模型,得到了模型無病周期解的穩定性和系統持久性的結論,并通過數值模擬驗證了結論的正確性.證明了基本再生數是傳染病最終消除和一致持久生存的閥值條件,若R0<1,無病周期解是全局漸近穩定的,即疾病將最終消除；若R0>1,疾病一致持續生存.

本文所研究的模型與文獻[8-9]中所討論的不具有階段結構的周期傳染病模型相比,動力學性態大致相同.可以得出結論,在周期SEIR模型中引入階段結構在某種程度上不會改變系統的動力學性態;但另一方面,通過比較具有周期傳染率的傳染病模型與相應的引入階段結構的模型發現,研究成人病時如果忽略階段結構,將會高估基本再生數,從而高估傳染病的傳播風險.

[1] AIELLO W G, FREEDMAN H I. A time-delay model of single-species growth with stage structure[J]. Math Bios,1990,101(2):139-153.

[2] 胡寶安,陳博文,原存德. 具有階段結構的SI傳染病模型[J]. 生物數學學報,2005,20(1):58-64.

[3] SATTENSPIEL L, DIETZ K. A structured epidemic model incorporating geographic mobility among regions[J]. Math Bios,1995,128(S1/S2):71-91.

[4] WANG W, ZHAO X Q. An age-structured epidemic model in a patchy environment[J]. SIAM J Appl Math,2005,65(5):1597-1614.

[5] ZHANG T L, TENG Z D. On a nonautonomous SEIRS model in epidemiology[J]. Bull Math Biol,2007,69(8):2537- 59.

[6] 胡新利,周義倉. 具有周期傳染率的SIR傳染病模型的周期解[J]. 生物數學學報,2008,23(1):91-100.

[7] BACAER N. Approximation of the basic reproduction number for vector-borne disease with a periodic vector population [J]. Bull Math Biol,2007,69(3):1067-1091.

[8] BAI Z G, ZHOU Y C. Global dynamics of an SEIRS epidemic model with periodic vaccination and seasonal contact rate[J]. Nonlinear Anal:RWA,2012,13(3):1060-1068.

[9] NAKATA Y,KUNIYA T, TOSHIKAZU K. Global dynamics of a class of SEIRS epidemic models in a periodic environment[J]. J Math Anal Appl,2010,363(1):230-237.

[10] WANG W, ZHAO X Q. Threshold dynamics for compartmental epidemic models in periodic environments[J]. J Dyn Diff Eqns,2008,20(3):699-717.

[11] ZHANG F, ZHAO X Q. A periodic epidemic model in a patchy environment[J]. J Math Anal Appl,2007,325(1):496-516.

[12] ZHAO X Q. Dynamical Systems in Population Biology[M]. New York:Springer-Verlag,2003.

2010 MSC:37N25

(編輯 余 毅)

Dynamic Behavior of a Periodic SEIR Epidemic Model with Stage-structure

DU Yanfei, XIAO Peng, CAO Hui

(DepartmentofMathematics,ShaanxiUniversityofScienceandTechnology,Xi’an710021,Shaanxi)

In this paper, we divide a population into two stages: immature stage and mature stage, and assume that disease transmission occurs only in mature individuals. Then we establish a periodc SEIR epidemic model with stage structure. We establish the global dynamics for disease-free periodic solution and discuss the uniform persistence of the system. Finally, the numerical simulations indicate the theoretical result is correct.

periodic epidemic model; stage-structured; the basic reproduction number; stability

2016-03-03

國家自然科學基金(11301314)和陜西省自然科學基金(2014JQ1025)

杜燕飛(1984—),女,講師,主要從事微分方程與生物數學的研究,E-mail:duyanfei@sust.edu.cn

O175

A

1001-8395(2017)01-0073-05

10.3969/j.issn.1001-8395.2017.01.012