門限已實現隨機波動率模型及其實證研究

吳鑫育，李心丹，馬超群

(1. 安徽財經大學金融學院，安徽 蚌埠 233030；2. 南京大學工程管理學院，江蘇 南京 210093；3. 湖南大學工商管理學院，湖南 長沙 410082)

?

門限已實現隨機波動率模型及其實證研究

吳鑫育1，2，李心丹2，馬超群3

(1. 安徽財經大學金融學院，安徽 蚌埠 233030；2. 南京大學工程管理學院，江蘇 南京 210093；3. 湖南大學工商管理學院，湖南 長沙 410082)

為了捕獲資產收益率均值和波動率雙重非對稱性, 以及充分利用包含豐富日內信息的高頻數據來提取波動率信息, 將門限效應和已實現波動率測度同時引入標準的隨機波動率(SV)模型中, 構建了門限已實現SV(TRSV)模型對資產收益率的波動率建模. 進一步, 基于有效重要性抽樣(EIS)技巧, 給出了TRSV模型的極大似然(ML)參數估計方法. 蒙特卡羅模擬實驗表明, EIS-ML參數估計方法是有效的. 最后, 采用上證綜合指數和深證成份指數日內高頻數據對TRSV模型進行了實證檢驗. 結果表明: TRSV模型相比已實現SV(RSV)模型具有更好的數據擬合效果, 能夠有效地刻畫我國股票市場收益率的波動率動態特征, 證明了我國股票市場收益率具有強的波動率持續性以及顯著的均值和波動率雙重非對稱性。

隨機波動率; 門限效應; 非對稱性; 已實現波動率; 有效重要性抽樣

1 引言

資產收益率的波動率在資產組合配置、風險管理以及期權定價中都扮演著重要的角色。因此研究波動率動態性特征, 對波動率進行建模, 具有重要的理論價值和實踐意義。 研究表明, 資產收益率的波動率具有時變性和聚集性。隨機波動率(SV)模型被廣泛應用于建模波動率的這種動態特征。SV模型假設條件方差由隱含的AR(1)隨機過程生成, 由于其在建模上的靈活性以及實際中對金融時間序列擬合的優越表現, 它在金融計量經濟學文獻中引起了廣泛的關注[1-4]。

標準的SV模型對于描述資產收益率序列的經驗特征事實仍過于局限。近年來, 越來越多的研究發現, 利好消息(資產收益率正向沖擊)和利空消息(資產收益率負向沖擊)對資產收益率的波動率的影響具有非對稱性。對這種現象(波動率非對稱性)的一種經典解釋為“杠桿效應”(Leverage effect)[5- 6]。標準的SV模型不能捕獲杠桿效應。為了克服這個問題, Harvey和Shephard[7]、Jacquier等[8]和Yu Jun[9]將杠桿效應引入標準的SV模型, 構建了杠桿SV(LSV)模型對波動率進行建模, 研究發現其具有更好的數據擬合效果。最近, So等[10]提出對波動率非對稱性的另一種解釋——門限效應(Threshold effect)。基于此, 他們提出了一個新的對波動率非對稱建模的思路: 將門限效應引入標準的SV模型, 構建了門限SV(TSV)模型對波動率進行建模。與LSV模型只能捕獲單一的波動率非對稱性相比, TSV模型由于能夠同時捕獲資產收益率均值和波動率雙重非對稱性而具有更好的數據擬合效果, 并引起了學者們廣泛的關注, 例如Asai和McAleer[11]、Chen等[12]、So 和Choi[13-14]、Wu Xinyu等[15]和吳鑫育等[16-17]。

傳統的波動率模型(例如GARCH模型和SV模型)采用日度收益率數據建模, 并以此來提取波動率信息。由于低頻日度收益率數據包含的信息有限, 不能完全反映資產價格日內實際變動情況, 造成提取的波動率信息往往存在偏差。特別是在金融市場高波動時期, 這種偏差愈加明顯, 進而造成風險度量和期權定價大的偏差。近年來, 隨著電子化交易的普及和信息存儲技術的發展, 包含豐富日內信息的高頻數據已經廣泛可得, 基于高頻數據構建的已實現波動率測度在金融計量經濟學文獻中獲得了廣泛的關注[18-21]。為了充分利用已實現波動率測度所包含的豐富日內信息, Takahashi等[22]最先將已實現波動率測度引入標準的SV模型, 構建了對日度收益率與已實現波動率測度同時建模的已實現SV(RSV)模型。Barndorff-Nielsen和Shephard[21]研究表明, 在理想的市場條件下, 已實現波動率是真實日度波動率的漸近一致估計量。但實際中由于存在市場微觀結構噪聲(例如買賣報價差和非同步交易)和非交易時間(例如隔夜和午休時間), 已實現波動率是真實日度波動率的一個有偏估計。基于RSV模型能夠同時給出已實現波動率測度的偏差與參數估計, 提高風險度量準確性。隨后, 眾多學者對RSV模型進行了廣泛的研究, 例如Koopman和Scharth[23]、Shirota等[24]、Venter和de Jongh[25]、Zheng Tingguo和Song Tao[26]和Takahashi等[27]。但到目前為止, 據我們所知, 國內對RSV模型的研究還鮮有見到, 且已有關于RSV模型的研究沒有考慮到資產收益率均值和波動率(雙重)非對稱性。

基于以上認識, 為了捕獲資產收益率均值和波動率雙重非對稱性, 同時充分利用包含豐富日內信息的高頻數據來提取波動率信息, 結合TSV和RSV模型的建模思想, 本文在標準的SV模型中同時引入門限效應和已實現波動率測度, 構建門限已實現SV(TRSV)模型對資產收益率的波動率進行建模。為了估計TRSV模型的參數, 給出有效、計算量小且易于實現的基于有效重要性抽樣(Efficient Importance Sampling, EIS)技巧的極大似然(ML)參數估計方法。最后, 采用上證綜合指數和深證成份指數日內高頻數據對構建的TRSV模型進行實證檢驗。

2 模型設定

標準的SV模型設定為:

xt=ψ0+ψ1xt-1+σexp(ht/2)εt,εt～i.i.d.(0,1)

(1)

ht+1=φht+γηt+1,ηt+1～i.i.d.N(0,1)

(2)

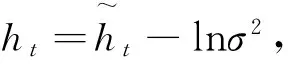
標準的SV模型能夠有效地捕獲時變波動率和波動率聚集性, 但它對于描述金融資產收益率序列的其它一些重要特征事實仍過于局限。根據So等[10]的研究, 正的和負的資產收益率對均值和波動率過程的行為都會產生不同的影響, 即存在均值和波動率雙重非對稱性。標準的SV模型不能捕獲資產收益率的這一重要特征事實。此外, 標準的SV模型僅針對低頻日度收益率數據建模, 沒有充分考慮包含豐富日內信息的高頻數據, 導致信息的損失, 從而造成提取的波動率信息可能存在偏差。基于以上分析, 本文結合So等[10]和Takahashi等[22]的建模思想, 將門限效應和已實現波動率測度同時引入標準的SV模型, 構建如下能夠捕獲資產收益率均值和波動率雙重非對稱性, 融合低頻日度收益率與高頻已實現波動率測度數據信息的TRSV模型對波動率進行建模:

xt=ψ0st-1+ψ1st-1xt-1+σst-1exp(ht/2)εt

(3)

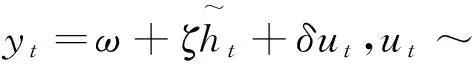
(4)

ht+1=φstht+γηt+1,ηt+1～i.i.d.N(0,1)

(5)

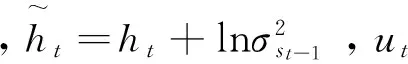
狀態變量st定義為

(6)

可以看到,st根據t時刻資產收益率xt的取值(小于0或大于等于0)在兩個區制之間轉換。如果在t時刻有利空消息到來, 資產價格下降(資產收益率負向沖擊), 則有xt<0和st=0; 反之, 如果在t時刻有利好消息到來, 資產價格上升(資產收益率正向沖擊), 則有xt≥0和st=1。因此, 參數ψ0st、ψ1st、σst和φst均在模型的兩個狀態st={0,1}之間轉換。當ψ0st和ψ1st在兩狀態下均相等, 則表明資產收益率不存在均值非對稱性, 反之表明存在均值非對稱性; 當σst和φst在兩狀態下均相等, 則表明資產收益率不存在波動率非對稱性, 反之表明存在波動率非對稱性。特別地, 如果σ0>σ1, 表明與利好消息相比, 同等程度的利空消息會引起資產收益率更高的波動性; 如果φ0≥φ1, 表明與利好消息相比, 同等程度的利空消息會引起資產收益率更強的波動率持續性, 即表明利空消息對資產收益率的影響程度要大于同等程度的利好消息對資產收益率的影響程度.

在TRSV模型(3)-(6)中, 均值和波動率過程均服從一個門限AR(1)模型, 本質上屬于Tong和Lim[29]提出的門限時間序列模型族。容易看到, 當ψ00=ψ01、ψ10=ψ11、σ0=σ1以及φ0=φ1,TRSV模型退化為RSV模型。

金融資產收益率普遍展現“偏斜”和“厚尾”的分布特征, 雖然SV模型結構本身能夠描述金融資產收益率數據一定的偏度和峰度, 但仍不足以擬合數據[30]。為此, 沿襲傳統SV模型文獻解決這個問題的思路, 本文采用能夠充分刻畫資產收益率分布的“偏斜”和“厚尾”特征的標準SKt分布[31](均值為0, 方差為1)作為TRSV模型中資產收益率新息εt的分布:

f(εt|ξ,ν)=

(7)

其中：

g[·|ν]是自由度為2<ν≤∞的標準學生t分布,ξ>0控制分布的偏斜度, 當lnξ>0, 分布正偏, 當lnξ<0, 分布負偏, 當lnξ=0, 標準SKt分布退化為標準學生t分布。

(8)

其中Γ(·)是Gamma函數。進一步, 當ν→∞, 學生t分布收斂于正態分布。

3 估計方法

由于包含不可觀測的狀態變量——波動率, SV模型的參數估計比較困難。一些參數估計方法, 例如廣義矩方法(GMM)、有效矩方法(EMM)和MCMC方法等已經用于SV模型的參數估計。但這些估計方法要么計算復雜, 要么不是有效的[32]。本文運用EIS-ML方法估計TRSV模型的參數。EIS-ML方法本質上屬于ML方法, 有著良好的統計性質, 如一致性、漸近正態性, 且計算量相對較小、易于實現, 因此該方法相比其它估計方法具有明顯的優越性。

設x={x0,x1,…,xT}′和y={y1,y2,…,yT}′是觀測值向量,h={h1,h2,…,hT}′是不可觀測狀態向量(h0當作未知參數進行估計)。TRSV模型的似然函數可以寫為：

(9)

其中Θ是TRSV模型的參數向量,p(x,y,h;Θ)是x,y和h的聯合密度函數, 可以寫為：

(10)

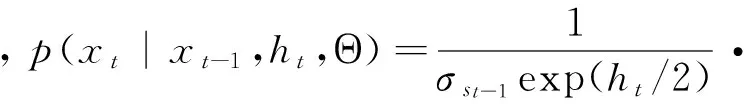
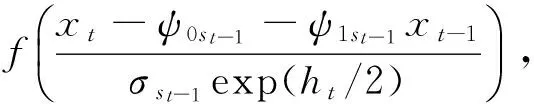
實際中, 式(9)是一個復雜的高維積分, 無法采用數值方法直接求解。為了克服這個問題, 本文運用EIS技巧來估計(9)。EIS技巧由Richard和ZhangWei[33]提出, 它易于實現, 且可以獲得SV模型高維積分似然函數的全局精確蒙特卡羅逼近。根據Richard和ZhangWei[33]的研究, 設定EIS密度的形式為:

(11)

(12)

其中kt(ht|xt-1,ht-1,at)是預先確定的參數化密度核函數,at是EIS輔助參數。

本文選取密度核函數

kt(ht|xt-1,ht-1,at)=p(ht|xt-1,ht-1,Θ)

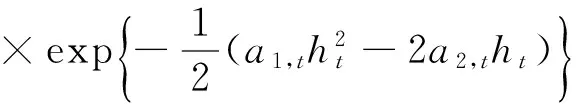
定義EIS輔助參數為at′=(a1,t,a2,t)。此時EIS密度mt(ht|xt-1,ht-1,at)是正態密度, 且其均值與方差分別為：

(13)

(14)

TRSV模型似然函數(9)可以改寫為：

L(x,y;Θ)=χ1(x0,h0;a1)·

(15)

其中χT+1(·)≡1。由此, 得到似然函數L(x,y;Θ)的EIS-蒙特卡羅估計為：

(16)

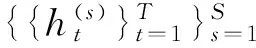
EIS技巧旨在通過選擇合理的輔助參數向量at, 以最小化式(16)的蒙特卡羅估計方差。根據Richard和ZhangWei[33]的研究, 它可以通過求解如下向后遞歸的輔助最小二乘問題實現:

(17)

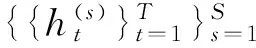
綜合起來, 估計TRSV模型似然函數的EIS算法具體步驟如下:

步驟2：向后遞歸地求解最小二乘問題(17), 或等價地作如下的線性回歸(t:T→1):

(18)

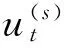
步驟4：重復步驟2和3, 直到收斂;

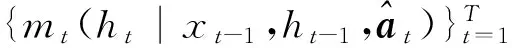
得到TRSV模型參數的EIS-ML估計為:

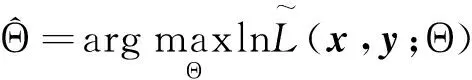
(19)

(20)

4 模擬實驗

這部分構建蒙特卡羅模擬實驗檢驗第3部分給出的EIS-ML參數估計方法的精確性和有限樣本性質。設定TRSV-SKt模型真實參數值為:ω=-0.5，ζ=1，δ=0.4，ψ00=0，ψ01=0，ψ10=-0.1，ψ11=0.1，σ0=0.015，σ1=0.014，φ0=0.95，φ1=0.97,γ=0.24，ξ=1，ν=30。參數值的設定基于第5部分的實證結果。根據“真實的”TRSV-SKt模型(3)-(7)模擬生成T=2000個樣本長度的觀測序列(收益率及對數已實現波動率序列)。對每一模擬的觀測序列, 運用EIS-ML方法進行估計, 重復模擬和估計實驗50次獲得參數估計的均值、標準差和均方根誤差(RMSE)。EIS-ML算法采用MATLAB軟件編程, 在Windows7計算機上實現。

表1給出了數值模擬的實驗結果。可以看到, 除了參數ν的估計存在輕微的高估外, 其它參數估計的均值均接近于相應的真實值, 估計標準差也都非常小, 表明EIS-ML估計方法是比較精確的。參數估計的RMSE都接近于標準差, 表明估計的有限樣本偏差很小。綜上, 運用EIS-ML方法估計TRSV-SKt模型, 可以獲得合理和有效的參數估計結果。

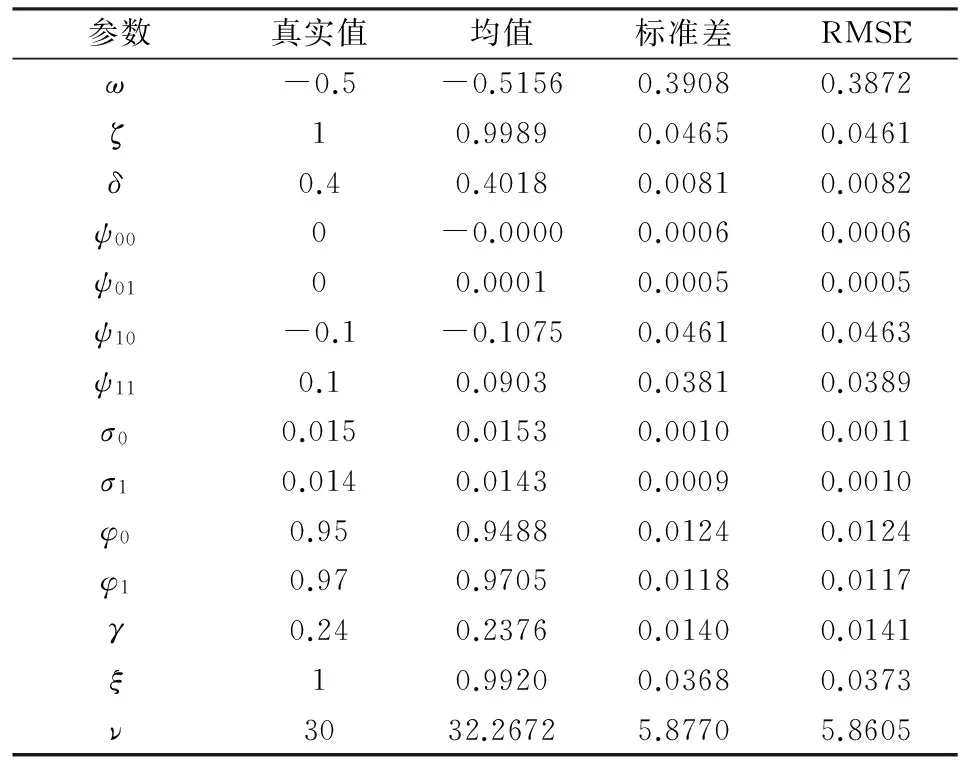
表1 數值模擬結果

注: EIS抽樣數S=32, 迭代5次, 重復模擬實驗50次獲得參數估計的均值、標準差和均方根誤差(RMSE)。

5 實證研究

5.1 數據與已實現波動率測度

本文采用上證綜合指數和深證成份指數日度收盤價格和日內5分鐘高頻交易價格數據作為研究樣本。5分鐘抽樣頻率的選擇是基于對已實現波動率的估計偏差與方差(市場微觀結構噪聲與信息損失)的權衡。鑒于我國股票市場在2005年開始實施了重大市場改革, 本文數據抽樣的時間跨度為2005年1月4日至2014年12月2日, 兩指數均為2401個日度觀測值和115248個日內觀測值。所有數據均來源于天軟數據庫。

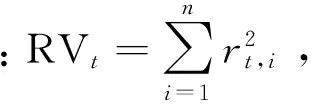
Barndorff-Nielsen和Shephard[21]研究表明, 在不存在市場微觀結構噪聲以及資產可一直連續交易的情形下, 已實現波動率RV依概率收斂于積分波動率(IntegratedVolatility,IV)或真實日度波動率。然而, 實際中由于存在市場微觀結構噪聲以及非交易時間, 已實現波動率并非積分波動率的無偏估計, 而是存在著向上(源于市場微觀結構噪聲)或向下(源于非交易時間)的偏差, 例如趙樹然等[34], 劉志東和嚴冠[35]。

表2給出了上證綜合指數和深證成份指數日度收益率(xt)和對數已實現波動率(yt)的描述性統計量。從表2可以看到, 兩指數日度收益率的分布均呈現負偏態(偏度<0), 且存在厚尾特征(峰度>3), 兩指數收益率都拒絕正態分布的假定(Jarque-Bera統計量顯著)。兩指數對數已實現波動率均呈現正偏態(偏度>0), 也都拒絕正態分布的假定(Jarque-Bera統計量顯著), 但比較接近于正態分布(峰度接近于3,Jarque-Bera值相對較小)。滯后10階的Ljung-Box檢驗結果表明, 兩指數日度收益率與對數已實現波動率序列都存在顯著的自相關性。ARCH效應檢驗表明, 兩指數日度收益率與對數已實現波動率序列都存在顯著的異方差性, 這也肯定了引入SV模型建模波動率的合理性。

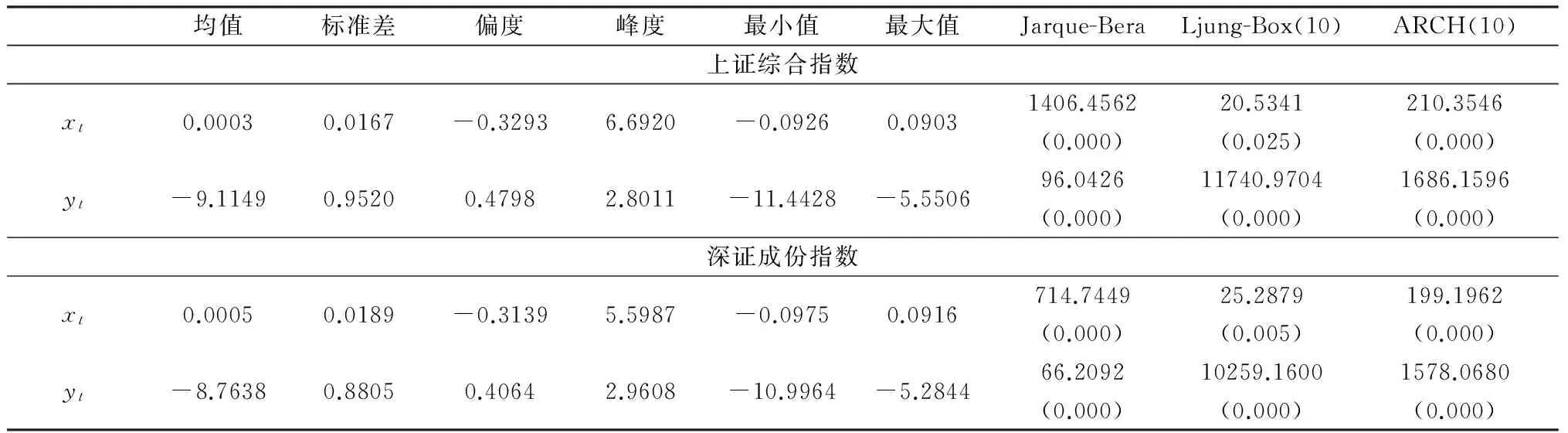
表2 日度收益率(xt)與對數已實現波動率(yt)的描述性統計量

注: ()中是檢驗統計量p-值。

圖1和圖2給出了上證綜合指數和深證成份指數日度收盤價格、日度收益率、經驗收益率密度及已實現波動率圖。從圖1和圖2可以看出, 兩指數日度收益率序列在抽樣階段內均展現明顯的波動率時變性和波動率聚集性特征, 均具有典型的厚尾分布特點, 且呈現非對稱的分布, 對數已實現波動率Q-Q圖表明其接近于正態分布。

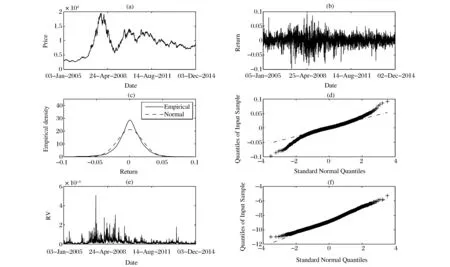
圖2 深證成份指數: (a) 日度收盤價格; (b) 日度收益率; (c) 經驗收益率密度; (d) 收益率Q-Q圖; (e) 已實現波動率; (f) 對數已實現波動率Q-Q圖

5.2 參數估計結果

運用第3部分給出的EIS-ML參數估計方法以及5.1節給出的上證綜合指數和深證成份指數數據, 得到TRSV模型(TRSV-N模型、TRSV-t模型和TRSV-SKt模型, 其中:N代表正態分布,t代表學生t分布,SKt代表偏斜學生t分布)的參數估計結果如表3和表4所示。為了比較, 表3和表4也給出了RSV模型(RSV-N模型、RSV-t模型和RSV-SKt模型)的參數估計結果。

從表中可以看到, 上證綜合指數和深證成份指數已實現波動率的線性偏差修正參數ω的估計值均明顯小于0, 表明中國股票市場的非交易時間效應要強于微觀結構噪聲效應, 兩指數已實現波動率均存在線性偏差。上證綜合指數ω估計值的絕對值大于深證成份指數ω估計值的絕對值, 表明上證綜合指數已實現波動率的線性偏差大于深證成份指數已實現波動率的線性偏差。兩指數已實現波動率的非線性偏差修正參數ψ的估計值均接近于1, 表明已實現波動率不存在明顯的非線性偏差, 與Hansen等[36]基于美國股票市場數據的實證結果一致。

在RSV模型中, 兩指數收益率自相關系數ψ1的估計值在0.03至0.05之間, 都接近于0, 表明兩指數收益率序列均存在弱的自相關性。在TRSV模型中, 兩指數收益率自相關系數ψ10和ψ11的估計值符號相反, 表明中國股票市場收益率存在均值非對稱性。在區制xt<0，ψ10估計值為負, 在區制xt≥0，ψ11估計值為正, 與So等[10]的估計結果一致, 這可以解釋上證綜合指數和深證成份指數收益率序列的弱自相關性。σ0的估計值均不同于σ1的估計值, 表明中國股票市場收益率存在波動率非對稱性, 且σ0估計值均大于σ1估計值, 說明與利好消息相比, 同等程度的利空消息會引起中國股票市場更高的波動率, 也即利空消息對中國股票市場的影響大于同等程度利好消息對中國股票市場的影響。波動率持續性參數φ(RSV模型)、φ0和φ1(TRSV模型)的估計值均接近于1, 表明中國股票市場具有強的波動率持續性特征。φ1估計值均大于φ0估計值, 說明利好消息對中國股票市場的影響相比同等程度利空消息對中國股票市場的影響更具有持續性。這與吳鑫育等[16-17]基于2001年至2011年中國股票市場數據得到的研究結論正好相反, 說明中國股票市場正在經歷轉變, 投資者對消息的反應模式發生變化。綜上, 中國股票市場具有強的波動率持續性以及顯著的均值和波動率雙重非對稱性。

兩指數t分布和SKt分布參數(ξ,ν)的估計結果表明, 兩指數收益率新息分布的偏斜厚尾性并不顯著(ξ估計值接近于1,ν估計值較大), 這與Takahashi等[27]的實證結果一致, 表明已實現波動率的引入消除了收益率新息分布的偏斜厚尾性, 因此偏斜厚尾分布并不總能改進已實現波動率模型的數據擬合效果。從對數似然值和AIC值來看,TRSV模型在滬深股市均具有比RSV模型更好的數據擬合效果, 滬市TRSV-t具有最好的數據擬合效果, 深市TRSV-N具有最好的數據擬合效果。

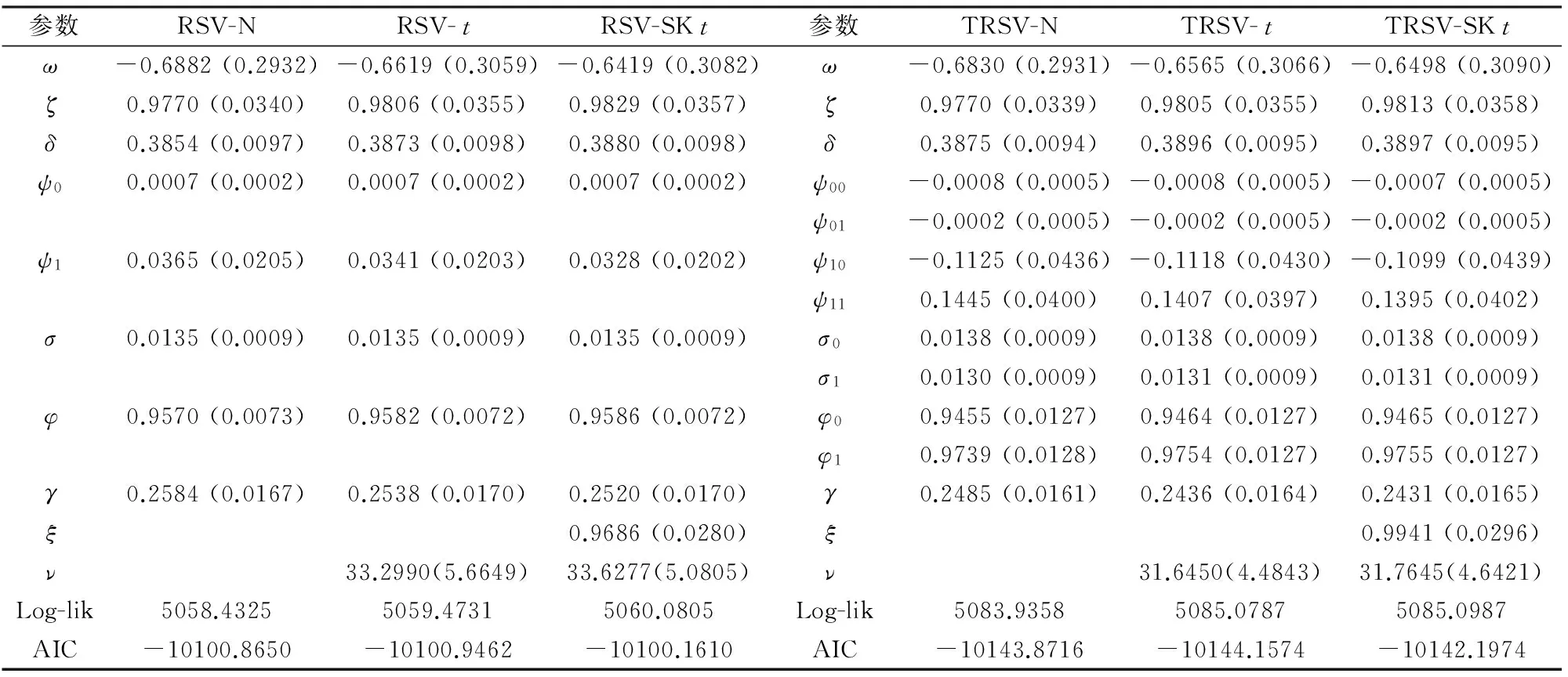
表3 參數估計結果: 上證綜合指數

注: EIS抽樣數S=32, 迭代5次;Log-lik是對數似然值;AIC是赤池信息準則; ()中是EIS-ML估計的漸近標準誤差。

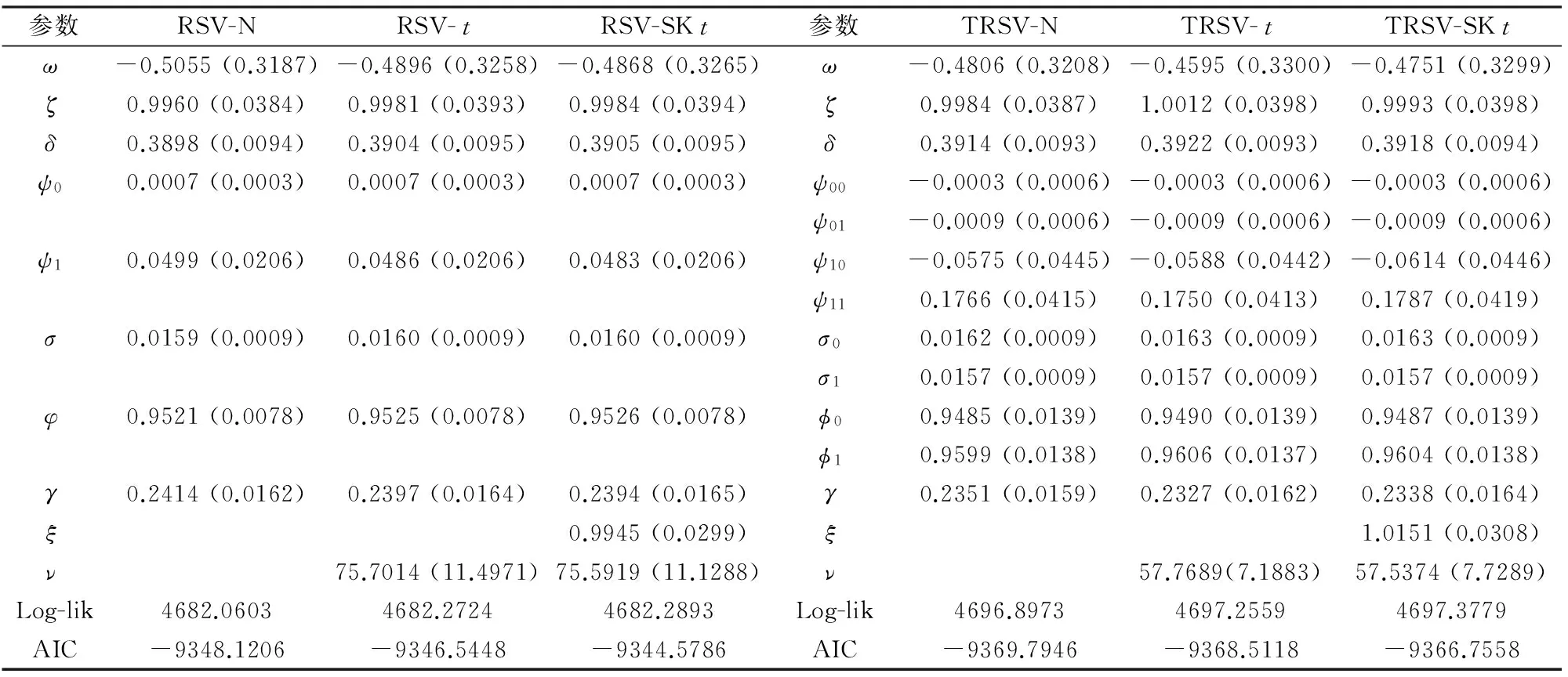
表4 參數估計結果: 深證成份指數

注: EIS抽樣數S=32, 迭代5次;Log-lik是對數似然值;AIC是赤池信息準則; ()中是EIS-ML估計的漸近標準誤差。

最后, 基于表3和表4給出的TRSV模型參數估計結果, 運用式(20)(取Ψ(x)=exp{x/2})計算得到上證綜合指數和深證成份指數濾過的波動率序列如圖3和圖4所示。可以看到, 波動率的變化特征與指數收益率的變化特征基本吻合, 表明TRSV模型能夠較好地描述兩指數收益率變化的時變波動率特征。特別地, 從圖3和圖4還可以看到, 在2008-2009年全球金融危機和2010年歐債危機期間, 中國股票市場表現出較高的波動性。

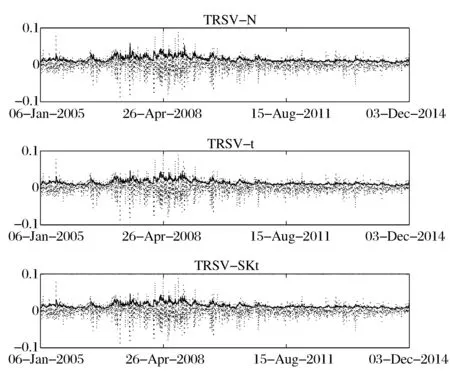
圖3 波動率估計: 上證綜合指數

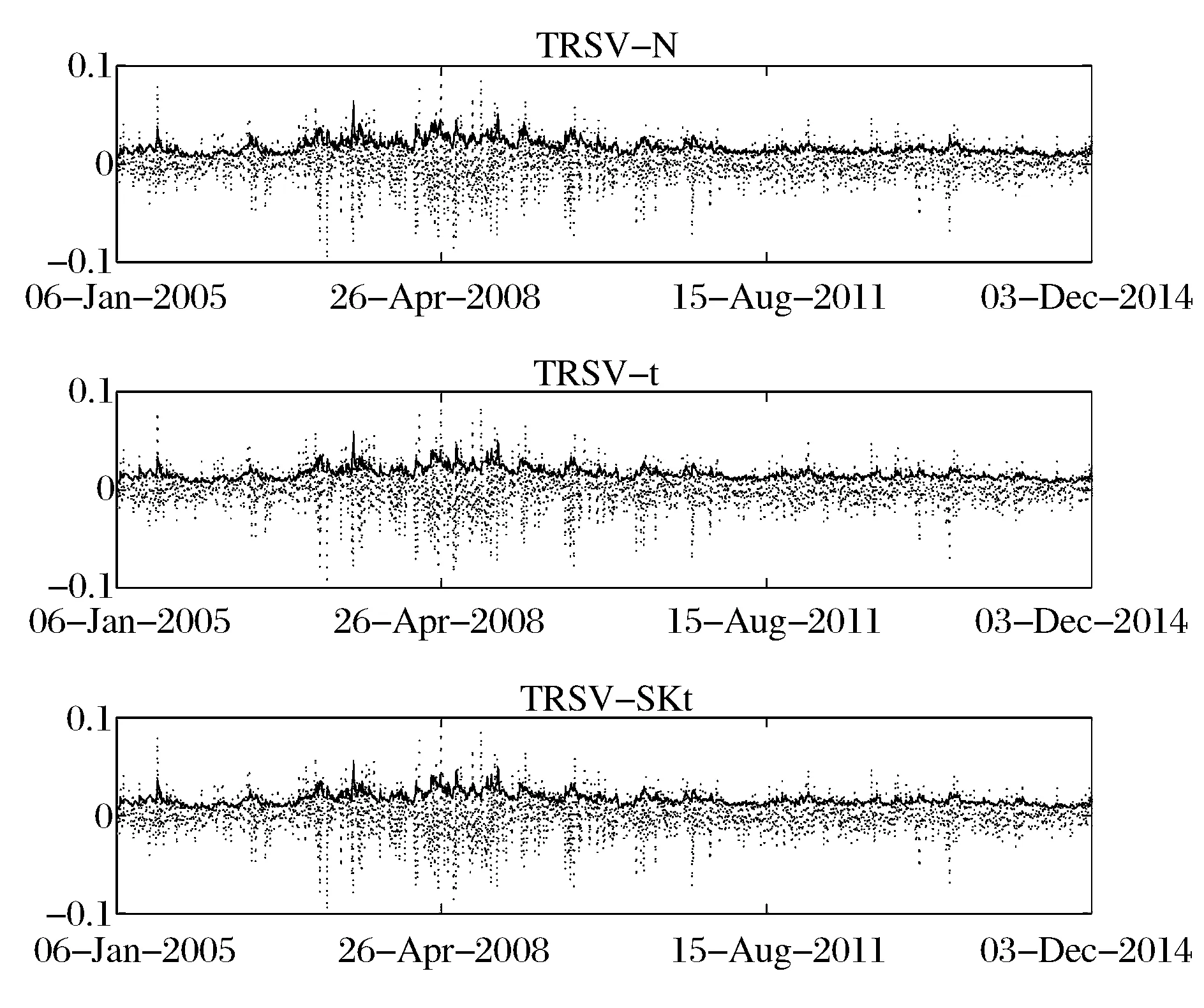
圖4 波動率估計: 深證成份指數

6 結語

本文將門限效應與已實現波動率測度同時引入標準的SV模型中, 構建了TRSV模型對波動率建模。該模型能夠捕獲資產收益率均值和波動率雙重非對稱性, 同時充分利用了包含豐富日內信息的高頻數據, 基于該模型可以獲得更為精確的波動率信息。為了估計TRSV模型的參數, 本文給出有效、計算量小且易于實現的EIS-ML參數估計方法。蒙特卡羅模擬實驗表明, 該參數估計方法是有效的。采用上證綜合指數和深證成份指數日內高頻數據, 本文對構建的TRSV模型進行了實證檢驗。結果表明: TRSV模型相比RSV模型具有更好的數據擬合效果, 能夠有效地刻畫我國股票市場收益率的波動率動態特征, 捕獲2008-2009年全球金融危機和2010年歐債危機; 中國股市具有強的波動率持續性, 并且存在顯著的均值和波動率雙重非對稱性, 具體而言, 利空消息相比同等程度的利好消息會引起中國股票市場更高的波動率以及更低的波動率持續性, 說明利空消息對中國股票市場的影響大于同等程度利好消息對中國股票市場的影響, 且利空消息對中國股票市場影響的持續性相比利好消息對中國股票市場影響的持續性要低。本文模型有助于深刻揭示股票市場對消息的反應模式。同時, 本文模型充分利用了市場上可用的信息(高頻數據信息)提取波動率, 為資產定價、投資組合構造以及風險管理的研究提供了參考。

[1] Jacquier E, Polson N G, Rossi P E. Bayesian analysis of stochastic volatility models[J]. Journal of Business & Economic Statistics, 2002,20(1):69-87.

[2] Kim S, Shephard N, Chib S. Stochastic volatility: Likelihood inference and comparison with ARCH models[J]. Review of Economic Studies, 1998, 65(3): 361-393.

[3] 江良, 林鴻熙. 隨機波動率Hull-White模型參數估計方法[J]. 系統工程學報, 2016, 31(5): 633-642.

[4] 周艷麗, 吳洋, 葛翔宇. 一類高新技術企業專利權價值的實物期權評估方法——基于跳擴散過程和隨機波動率的美式期權的建模與模擬[J]. 中國管理科學, 2016, 24(6): 19-28.

[5] Black F. Studies of stock price volatility changes[C]//Proceedings of the 1976 Meeting of Business and Economic Statistics Section, American Statistical Association, 1976: 177-181.

[6] Christie A A. The stochastic behavior of common stock variances[J]. Journal of Financial Economics, 1982, (10): 407-432.

[7] Harvey A C, Shephard N. The estimation of an asymmetric stochastic volatility model for asset returns[J]. Journal of Business & Economic Statistics, 1996, 14(4): 429-434.

[8] Jacquier E, Polson N G, Rossi P E. Bayesian analysis of stochastic volatility models with fat-tails and correlated errors[J]. Journal of Econometrics, 2004, 122(1): 185-212.

[9] Yu Jun. On leverage in a stochastic volatility model[J]. Journal of Econometrics, 2005, 127(2): 165-178.

[10] So M K, Li W K, Lam K. A threshold stochastic volatility model[J]. Journal of Forecasting, 2002, 21(7): 473-500.

[11] Asai M, McAleer M. Dynamic asymmetric leverage in stochastic volatility models[J]. Econometric Reviews, 2005, 24(3): 317-332.

[12] Chen C W S, Liu F C, So M K P. Heavy-tailed distributed threshold stochastic volatility models in financial time series[J]. Australian & New Zealand Journal of Statistics, 2008, 50(1): 29-51.

[13] So M K, Choi C Y. A multivariate threshold stochastic volatility model[J]. Mathematics and Computers in Simulation, 2008, 79(3): 306-317.

[14] So M K, Choi C Y. A threshold factor multivariate stochastic volatility model[J]. Journal of Forecasting, 2009, 28(8): 712-735.

[15] Wu Xinyu, Zhou Hailin. A triple-threshold leverage stochastic volatility model[J]. Studies in Nonlinear Dynamics & Econometrics, 2015, 19(4): 483-500.

[16] 吳鑫育, 周海林, 汪壽陽, 等. 雙杠桿門限隨機波動率模型及其實證研究[J]. 管理科學學報, 2014, 17(7): 63-81.

[17] 吳鑫育, 周海林. 中國股票市場的非對稱反應[J]. 系統工程, 2015, 33(8): 78-83.

[18] 瞿慧, 李潔, 程昕. HAR族模型與GARCH族模型對不同期限波動率的預測精度比較——基于滬深300指數高頻價格的實證分析[J]. 系統工程, 2015, 33(3): 32-37.

[19] 瞿慧, 程思逸. 考慮成分股聯跳與宏觀信息發布的滬深300指數已實現波動率模型研究[J]. 中國管理科學, 2016, 24(12): 10-19.

[20] Barndorff-Nielsen O E, Shephard N. Non-Gaussian Ornstein-Ulhlenbeck-based models and some of their uses in financial economics[J]. Journal of the Royal Statistical Society, Series B, 2001, 63(2): 167-241.

[21] Barndorff-Nielsen O E, Shephard N. Econometric analysis of realized volatility and its use in estimating stochastic volatility models[J]. Journal of the Royal Statistical Society: Series B, 2002, 64(2): 253-280.

[22] Takahashi M, Omori Y, Watanabe T. Estimating stochastic volatility models using daily returns and realized volatility simultaneously[J]. Computational Statistics & Data Analysis, 2009, 53(6): 2404-2426.

[23] Koopman S J, Scharth M. The analysis of stochastic volatility in the presence of daily realised measures[J]. Journal of Financial Econometrics, 2013, 11(1): 76-115.

[24] Shirota S, Hizu T, Omori Y. Realized stochastic volatility with leverage and long memory[J]. Computational Statistics & Data Analysis, 2014, 76: 618-641.

[25] Venter J H, de Jongh P J. Extended stochastic volatility models incorporating realised measures[J]. Computational Statistics & Data Analysis, 2014, 76: 687-707.

[26] Zheng Tingguo, Song Tao. A realized stochastic volatility model with Box-Cox transformation[J]. Journal of Business and Economic Statistics, 2014, 32(4): 593-605.

[27] Takahashi M, Watanabe T, Omori Y. Volatility and quantile forecasts by realized stochastic volatility models with generalized hyperbolic distribution[J]. International Journal of Forecasting, 2016, 32(2): 437-457.

[28] Taylor S J. Financial returns modelled by the product of two stochastic processes-a study of daily sugar prices[M]//Anderson O D. Time series analysis: Theory and practice 1. Amsterdam:North Holland, 1982: 203-226.

[29] Tong H, Lim K S. Threshold autoregression, limit cycles and cyclical data[J]. Journal of the Royal Statistical Society: Series B, 1980, 42(3): 245-292.

[30] 吳鑫育, 馬超群, 汪壽陽. 隨機波動率模型的參數估計及對中國股市的實證[J]. 系統工程理論與實踐, 2014, 34(1): 35-44.

[31] Lambert P, Laurent S. Modelling skewness dynamics in series of financial data using skewed location-scale distributions[R]. Discussion Paper, Catholic University of Louvain, 2002.

[32] Broto C, Ruiz E. Estimation methods for stochastic volatility models: A survey[J]. Journal of Economic Surveys, 2004, 18(5): 613-649.

[33] Richard J F, Zhang Wei. Efficient high-dimensional importance sampling[J]. Journal of Econometrics, 2007, 141(2): 1385-1411.

[34] 趙樹然, 姜亞萍, 任培民. 高頻波動率矩陣估計的比較分析——基于有噪非同步的金融數據[J]. 中國管理科學, 2015, 23(10): 19-29.

[35] 劉志東, 嚴冠. 基于半鞅過程的中國股市隨機波動、跳躍和微觀結構噪聲統計特征研究[J]. 中國管理科學, 2016, 24(5): 18-30.

[36] Hansen P R, Huang Zhuo, Shek H H. Realized GARCH: A joint model for returns and realized measures of volatility[J]. Journal of Applied Econometrics, 2012, 27(6): 877-906.

Threshold Realized Stochastic Volatility Model and its Empirical Test

WU Xin-yu1, 2，LI Xin-dan2，MA Chao-qun3

(1.School of Finance, Anhui University of Finance and Economics, Bengbu 233030, China;2.School of Industrial Engineering and Management, Nanjing University, Nanjing 210093, China;3.Business School, Hunan University, Changsha 410082, China)

Volatility in financial markets has attracted a great deal of attention from academics, policy makers and practitioners during the past decades, primarily because it plays a crucial role in many financial applications, such as portfolio selection, option pricing and risk management. It has been well-documented in the finance literature that the financial market volatility is not a constant but in fact changes over time and financial time series exhibits volatility clustering. In addition, many empirical researches have indicated that the mean and volatility of asset returns respond asymmetrically to market news. Recently, with the development of information technology, the availability of high frequency data means that it has become possible to measure the latent volatility using the so-called realized volatility (RV) measure. Under some assumptions, the RV is a consistent estimator of the true volatility. In the real market, however, the RV measure computed from high frequency return data suffers from microstructure noise. In this paper, both the threshold effects and realized volatility measure are incorporated into the standard stochastic volatility (SV) model and the threshold realized SV (TRSV) model is proposed to model the volatility of asset returns. The model is able to account for time-varying volatility and volatility clustering and capture simultaneously the mean and volatility asymmetries in asset return data. Also, this model, which uses high-frequency data containing valuable intraday information to extract volatility information, can estimate RV biases and parameters simultaneously. The lack of a closed-form expression of the likelihood function makes the estimation of the SV models being a challenging topic in the literature. In this paper, the efficient importance sampling (EIS) technique is adopted to implement the maximum likelihood (ML) estimation method for our proposed TRSV model. The Monte Carlo simulation study shows that the EIS-ML estimation method can provide appropriate and accurate inference for the parameters of the proposed model. Finally, the TRSV model is applied to the intraday high-frequency data of Shanghai Stock Exchange composite index and Shenzhen Stock Exchange component index of China. Empirical results show that the TRSV model captures the volatility dynamics appropriately and provides better fit to the data compared to the realized SV (RSV) model. Moreover, strong evidence of high persistence of volatility and the mean and volatility asymmetries is detected in Chinese stock markets.

stochastic volatility; threshold effect; asymmetries; realized volatility; efficient importance sampling

1003-207(2017)03-0010-10

10.16381/j.cnki.issn1003-207x.2017.03.002

2015-11-26；

2016-06-14

國家自然科學基金資助項目(71501001, 71431008); 教育部人文社科研究青年基金資助項目(14YJC790133); 中國博士后科學基金資助項目(2015M580416); 安徽省自然科學基金資助項目(1408085QG139); 安徽省高等學校省級優秀青年人才基金重點資助項目(2013SQRW025ZD)

吳鑫育(1982-), 男(漢族), 湖南衡山人, 安徽財經大學金融學院副教授, 南京大學工程管理學院博士后, 研究方向: 金融工程與風險管理, E-mail: xywu@hotmail.com.

F830.9

A