機器學習中K—means聚類算法的分析和應用
王子橋

摘 要:本文采用機器學習中的聚類算法對高水平足球聯賽五十名頂尖球員的進攻數據進行無監督聚類學習和分析,并以進球數、射正數和助攻數為評價指標,將球員分成三個類別。本文首先分析了K-means聚類算法的流程和特點,進而應用于對足球運動員比賽數據的聚類運算。對聚類后的分類結果進行分析和比較,從而找出球員的優勢劣勢。其結果不僅對球員個人發展有極大的指導作用,也對中國足球取長補短、提升自身能力有重要意義。
關鍵詞:K-means算法;聚類;機器學習
中圖分類號:TP18 文獻標識碼:A 文章編號:1671-2064(2017)04-0030-02
計算機是迄今為止最為高效的信息處理工具,特別是近年來隨著互聯網的發展,應用計算機輔助工作和學習已經成為常態。但普通計算機缺乏自主學習的能力,只是被動地執行人為設定好的程序。因此人們開始尋找一種能以與人類智能學習相似的方式進行數據處理的方法,于是人工智能應運而生。
從1997年深藍在國際象棋中戰勝卡帕羅耶夫,到2016年AlphaGo在圍棋中擊敗李世石,不難看出,人工智能的發展潛力十分巨大。然而,目前的人工智能仍處于十分初級的弱人工智能階段,想要進一步發展人工智能就必須探索新的更有效的方法。
近年來,人工智能領域中的重要方向——機器學習,得到了越來越多的重視,顧名思義,機器學習是通過經驗自動改進計算機算法的研究,[1]也就是說,機器學習能用數據或以往的經驗優化計算機程序的性能標準,在不斷進行自我學習的過程中,對機器自身程序算法進行優化。在機器學習中,聚類是一種極其重要的算法。聚類源于包括數學、計算機科學、經濟學、生物學等的許多領域,其工作原理是通過研究各個樣本之間的相似度,利用數學方法對樣本進行分類。[2]這其中,K-means算法是最為經典的聚類算法之一。K-means算法是聚類分析中一種基于劃分的算法,屬于無監督的學習,該算法是聚類分析中一種十分經典且非常高效的方法,具有高效率和相對可伸縮的優點,在處理大數據集時簡單快速,十分方便。[3]
1 K-means算法
作為一種無監督的聚類算法,K-means算法在解決多個樣本數據進行分類的問題時十分有效,給定一組樣本{},K-means算法將會把樣本聚成k個簇,具體步驟如下:
(1)根據給定的k值隨機選取k個質心{}。
(2)重復迭代兩步直到質心不變或變化很小:1)計算每一個樣本i應屬于的類別=argmin,2)對每一個類別j,重新計算它的質心,其中k是已知的聚類數,是樣本i與k個類別中最近的一類,質心位置是初始隨機選定的。其算法流程圖如圖1所示。
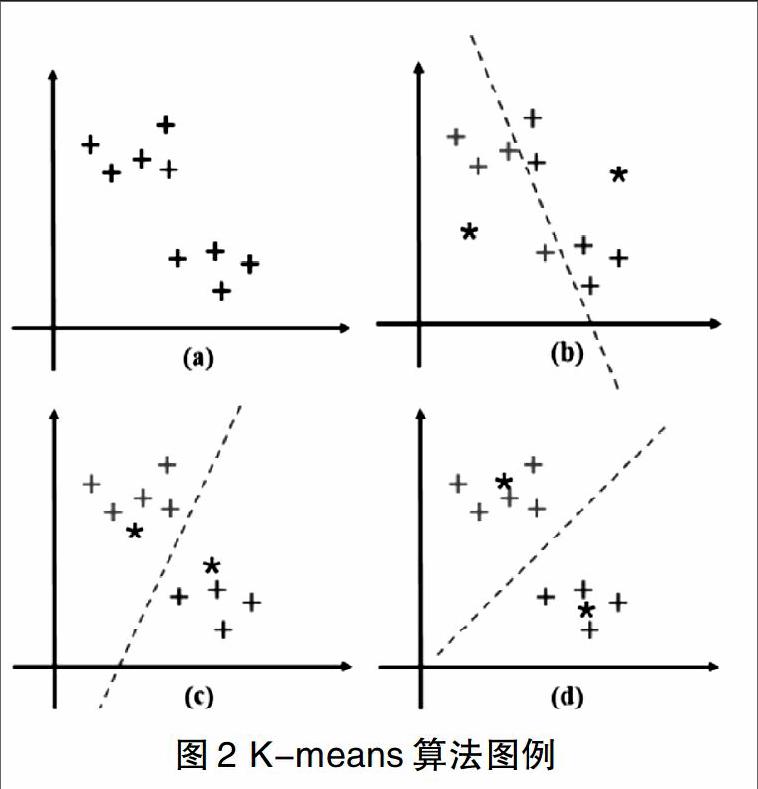
下面用算法圖例來展示K-means算法的具體運算流程,如圖2所示。
如上圖所示,數據的初始分布如圖(a)所示,數據點用二維平面的加號 ”+”表示,共9個數據點。在圖(b)中,用星號“*”表示K-means算法的初始聚類中心。根據上述算法流程,K-means通過計算初始聚類中心到數據點的歐氏距離對樣本點進行第一次分類,用紅色與綠色表明第一次的分類結果,結果如圖(b)所示。在第一次分類后,對每一類的全部樣本點重新計算質心,再次計算樣本與每個質心的距離進行下一次分類,結果如圖(c)。重復該過程直到聚類質心的位置不變或質心變化很小達到穩定狀態,結果如圖(d),最終得到了樣本的2分類結果。
由以上介紹,我們可以看出K-means算法操作簡便,分類效率高。在速度上有很明顯的優勢,特別是在處理大量復雜樣本時,K-means能利用比較各個樣本相似度特性的方法就使問題得到簡化,從而達到快速分類的目的。它的另一優點是時間復雜度較低,其時間復雜度可以表示為O(nkt)。n是數據集中對象的數量,k是類別數,t是迭代次數。也就是說,其時間復雜度是近于線性的,相對于其他的聚類算法復雜度較低。
然而K-means算法只能達到局部最優,因此在其k值的選擇和初始質心的選取上較難控制,不同取值會導致較大的差異.且K-means對數據源要求較高,只適用于球狀分布的聚類特性數據,不能處理非球狀分布或差別很大的樣本集,這是該算法一個很大的局限性。另外,因為迭代次數無法確定,K-means算法的算法不夠穩定,在某些特殊的數據集上可能導致其復雜度急劇增加,導致算法的運行效率較低。
2 球員數據應用
足球運動員在訓練或比賽中會有許多個人表現的數據,比如進球數、助攻數等等。對球員數據的合理分析有助于指導球員的訓練和提升技術水平。本文收集了歐洲范圍內五大高水平聯賽50名頂尖球員(排名榜前十名)的運動數據。由于所列球員都為進攻性球員,故采取進球數、助攻數、射門成功率為評價指標,其中射門成功率為 (進球數/射門數)*100%。由于各個數據的變化范圍不統一,因此首先對數據進行歸一化處理,再讀入K-means程序進行聚類分析。
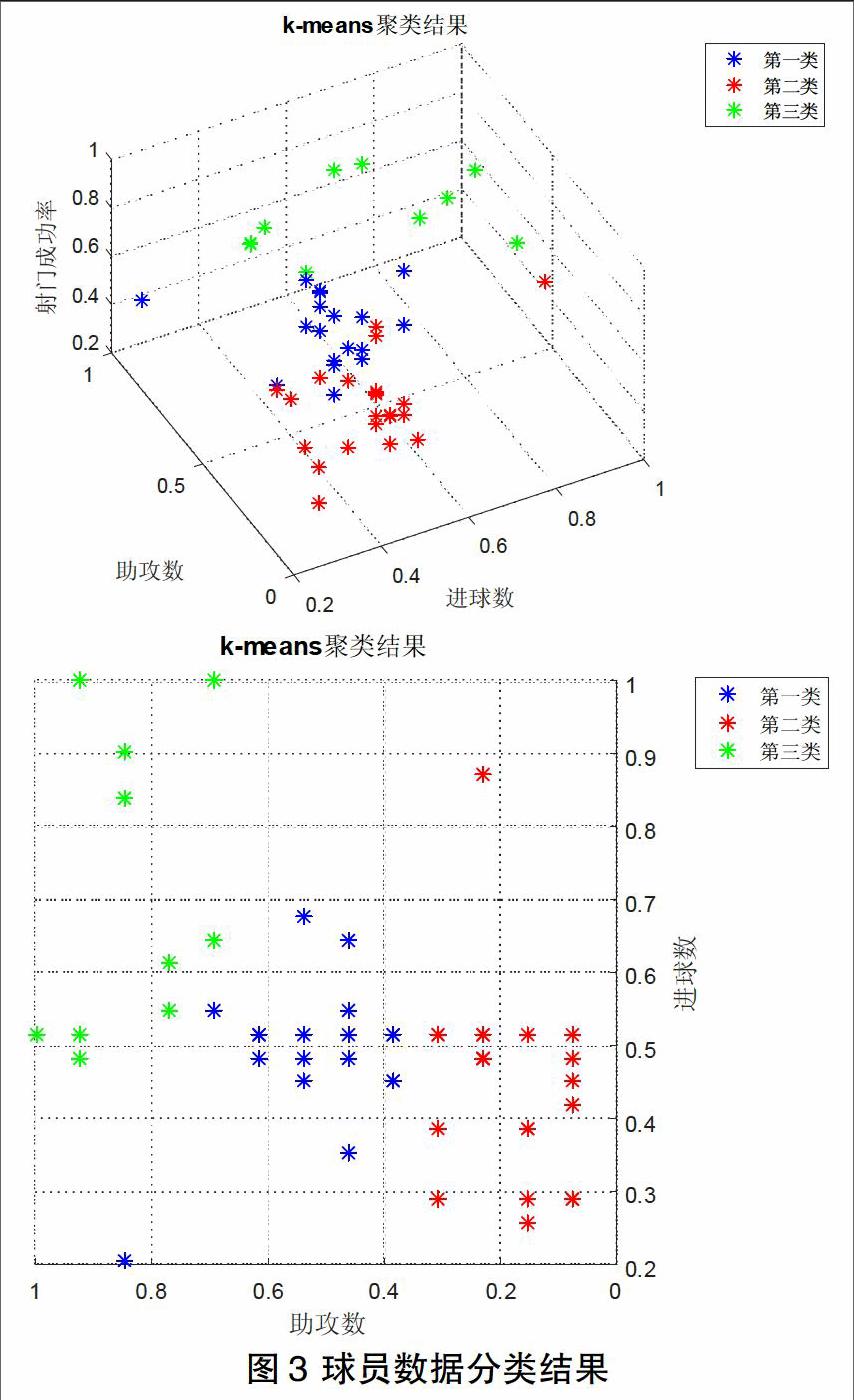
在經過歸一化處理之后,將50組數據讀入K-means算法程序,并通過進球數、助攻數和射門成功率三維坐標進行顯示,其分類結果如圖3所示。
由該分類結果我們可以看出,越靠近坐標為(1,1,1)的點說明球員的數據越突出。在本結果中,綠色類為數據較優秀的球員,藍色類為數據一般的球員,而紅色類為數據較差的球員。在助攻數和射門成功率上,綠色類都要明顯優于其他兩組,而在進球數上,三個類別沒有體現出明顯的分類差異。特別是,在助攻數這一評價標準中,三類的區分度尤其明顯,這也就意味著,助攻數和射門成功率是衡量一個優秀球員最為關鍵的因素,而不僅僅是考量進球數。這一點與人們一般認可進球數的常識相悖。因此要想成為一名優秀的足球運動員,除了在保證進球數的基礎上,提升助攻和射門成功率也是十分重要的方面。
但是,在本方法中也存在一定不足。比如數據的采集,總共選取了50名球員的運動數據,而且主要取自于頂尖排名,但并不一定能夠代表所有足球運動員的實際水平,具有一定的局限性。另一方面,本方法所分析的助攻數、進球數和射門成功率這三項指標并不能完全代表一個球員的場上表現,只是選取了三個可量化的評價指標,為了得到更為全面的評價結論,還需要更加全方位的分析和總結。
3 結語
本文分析了機器學習中無監督聚類算法K-means的詳細流程和典型應用。對該算法的實現過程、算法流程進行了仔細的分析和討論。并將該算法應用在對頂尖足球運動員運動數據的聚類分析上,以進球數、射正數和助攻數為評價指標,將球員分成三個類別。并對聚類后的分類結果進行分析和比較,發現助攻數是較進球數影響更大的因素,從而找出分辨球員的優劣的新標準。該結果對足球運動員個人能力的提升上意義重大,更對中國足球未來的發展有一定指導作用。
參考文獻
[1]曾華軍,張銀奎,等譯.《機器學習》Tom M Mitchell[M].機械工業出版社,2003.
[2]馬俊才,趙玉峰.基于分行維數的聚類分析研究[J].微生物學通報,1986.
[3]王穎,劉建平.基于改進遺傳算法的kmeans聚類分析[J].工業控制計算機,2011.

