動態頻譜抗干擾系統中跳頻序列研究*
李勝男,李永貴,閆 巖
(1. 解放軍理工大學 通信工程學院,江蘇 南京 210007;2. 南京電訊技術研究所,江蘇 南京 210007)
動態頻譜抗干擾系統中跳頻序列研究*
李勝男1,2,李永貴2,閆 巖1
(1. 解放軍理工大學 通信工程學院,江蘇 南京 210007;2. 南京電訊技術研究所,江蘇 南京 210007)
現有的跳頻序列,由于綜合性能不均衡,參數無法實時改變,無法直接應用于動態頻譜抗干擾系統中,因此迫切需要研究一種適用于動態頻譜抗干擾系統的動態跳頻序列。基于m偽隨機序列,提出了一種頻率數可根據通信環境實時變化的跳頻序列。仿真結果表明,與基于固定參數的頻率自適應跳頻序列相比,動態跳頻序列在均勻性、隨機性、漢明相關性等方面均具有更好的性能。
動態頻譜抗干擾;跳頻序列;任意頻率數;均勻性
0 引言
作為跳頻通信三大關鍵技術之一,跳頻序列對跳頻通信系統的性能有著決定性的影響。目前常見的跳頻序列主要有基于有限域的跳頻序列、基于混沌理論的跳頻序列以及基于密碼學的跳頻序列等[1-4]。然而,這些跳頻序列大多是針對頻率數為素數的整數次冪(即pk,p為素數)的跳頻系統而設計的,而實際的跳頻通信難以滿足可用頻率數為整數冪的要求[5]。特別地,在動態頻譜抗干擾系統[6-7]中,構成跳頻頻率表的頻率數、頻率值、分布帶寬等頻譜資源隨著頻譜感知的結果實時、動態變化,現有的跳頻序列由于綜合統計性能不均衡,參數無法實時改變,無法直接應用于動態頻譜抗干擾系統中。因此,研究適用于動態頻譜抗干擾系統的動態跳頻序列技術,是實現動態頻譜抗干擾系統必須要解決的問題。
文獻[8-9]基于重新映射思想,提出了一種頻率數為pk-pm的跳頻序列產生方法,但其從根本上并沒有跳出整數冪的思想。文獻[10]基于分段映射、奇偶交替思想,提出了一種任意頻率數跳頻序列構造方法,該方法生成的序列具有較好的一維均勻性,但二維均勻性和隨機性較差,同時頻率數難以實時改變。文獻[11]基于3DES算法,提出了一種任意頻率數跳頻序列構造方法,然而,3DES算法屬于公開算法,勢必還會經歷長期的攻擊考驗[12],而且,實際跳頻電臺中常采用的方法是,在單個m序列發生器上加非線性前饋邏輯,或者用幾個m序列發生器進行非線性組合,再通過抽頭選取,從而得到高度非線性的跳頻序列。
因此,本文首先基于m序列,通過抽頭模型,產生多組跳頻獨立序列。然后,根據頻譜感知得出的可用頻率數等系統參數對跳頻獨立序列進行偽隨機映射,提出一種頻率數實時可變的跳頻序列構造方法。仿真證明它在均勻性、隨機性、漢明相關性等方面均具有良好的統計性能,同時,頻率數能夠為任意值,且實時改變。
1 系統模型
動態頻譜抗干擾系統在傳統無線通信系統中引入動態頻譜接入思想,在對電磁環境實時、有效感知的基礎上,通過智能決策及動態調整通信參數,提高無線通信系統的電磁環境適應能力、抗干擾能力和多用戶組網高效性。如圖1所示,假設系統中共有N1個通信用戶Uk(k=1,…,N1),N2個干擾用戶Jk(k=1,…,N2)。假設每個通信周期分為四個階段:同步階段、頻譜感知階段、智能決策階段和通信階段。在時間同步階段,系統中所有通信用戶將本地的TOD調整為相同。完成時間同步后,系統進入頻譜感知階段(這一階段一直在進行,直到通信結束),所有通信用戶對頻譜環境進行感知,得到分布帶寬內所有可用頻譜。在智能決策階段,網控中心根據感知結果得到本周期內系統的通信參數(如頻率數、跳頻間隔、功率、調制方式等)以及系統所要實現的最優目標,對各通信用戶的頻譜分配和使用進行決策。在通信階段,各通信用戶根據決策結果完成通信。
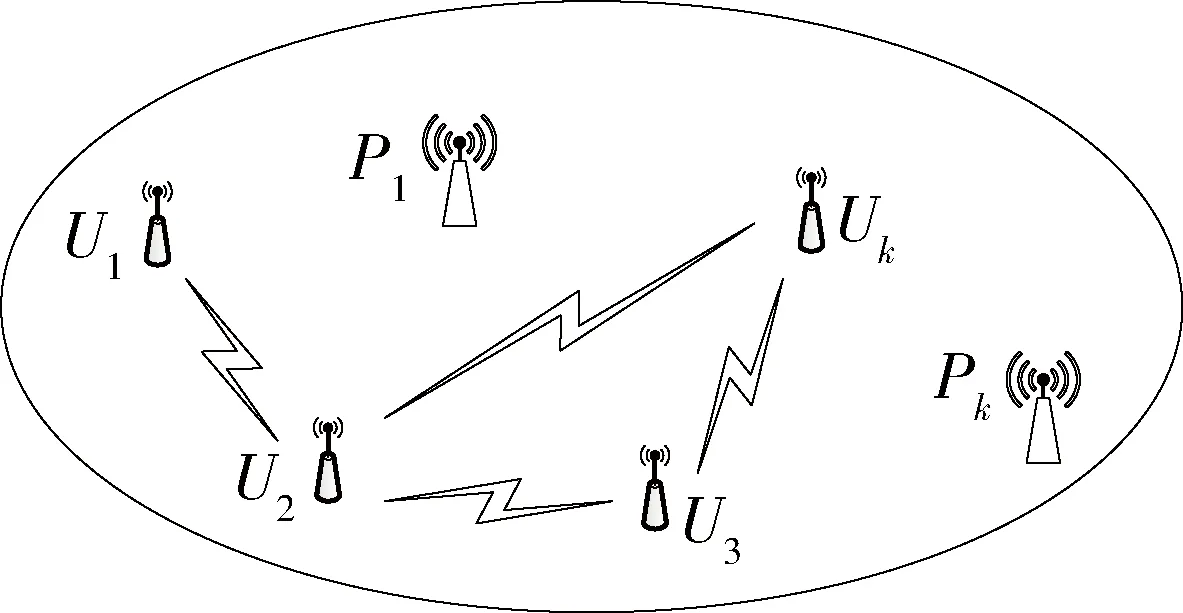
圖1 復雜電磁環境中的動態頻譜抗干擾系統模型
為實現動態頻譜抗干擾通信,必須設計一種能使信號在無干擾、可用信道上傳輸的動態跳頻序列。假設第k個周期內無干擾、可用頻率數為qk,則動態跳頻序列可表示為F={ft|t=1,2,3,…},其中,ft∈{1,2,…,qk}。
2 動態跳頻序列生成算法
基于上述假設,動態跳頻序列可以根據動態參數實時生成。動態跳頻序列生成原理圖如圖2所示。

圖2 動態跳頻序列生成原理圖
2.1 獨立跳頻序列的產生
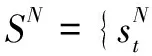
32[(at+4+u2)mod2]+16[(at+6+u3)mod2]+
8[(at+8+u4)mod2]+4[(at+10+u5)mod2]+
2[(at+12+u6)mod2]+(at+14+u7)mod2
(1)
2.2 序列選擇
首先,由實時感知得到的頻率數為qk,根據公式(2)設置門限THm:
THm=qk
(2)
然后,根據公式(3),將N條跳頻序列的t時刻的跳頻碼與門限值逐一比較,找到第一個小于門限值的跳頻碼,得到參數m。
(3)
2.3 偽隨機映射
根據公式(4),并依據k周期內可用的頻率數,得到t時刻的跳頻碼。通過時鐘驅動,從而得到所需長度的跳頻序列:
(4)
3 仿真及性能分析
跳頻序列的綜合統計性能對跳頻通信系統起著決定性作用,為了驗證本文提出方法產生的跳頻序列的性能,本文從均勻性、隨機性、漢明相關性等方面對跳頻序列進行性能分析,并與工程上應用廣泛的基于固定參數的頻率自適應跳頻序列比較分析。仿真參數如表1所示。
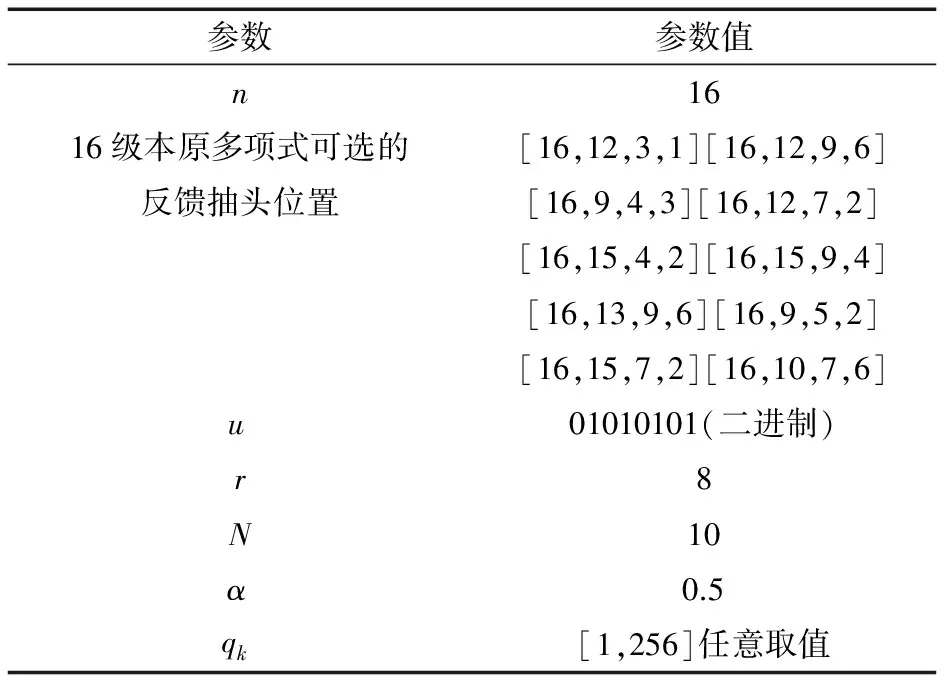
表1 仿真參數
3.1 均勻性
均勻性通常分為一維均勻性和二維均勻性。一維均勻性是指各跳頻碼出現的概率相等,即P(ft=i)=1/qk(i=1,…,qk)。二維均勻性是指各跳頻碼對連續出現的概率相等,即跳頻碼ft出現后緊接著出現跳頻碼ft的聯合概率相等,P(ft=i,ft+1=j)=1/qk2。其中,i,j=1,…,qk。
序列的均勻性常用χ2檢驗法驗證。以檢驗一維均勻性為例,檢驗假設H0={序列服從均勻分布},則檢驗統計量為:
(5)
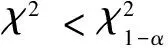
均勻性仿真曲線如圖3所示。由圖3可知,基于固定參數的頻率自適應跳頻序列的均勻性卡方檢測值明顯高于理論參考值,而動態跳頻序列的卡方檢測值均低于理論參考值。因此,可以認為動態跳頻序列具有較好的均勻性。

圖3 均勻性仿真曲線
3.2 隨機性
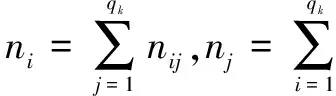
(6)


圖4 隨機性仿真曲線
隨機性仿真曲線如圖4所示。由圖4可知,在碼子距離小于10時,基于固定參數的頻率自適應跳頻序列的隨機性卡方檢測值高于理論參考值,而動態跳頻序列的卡方檢測值始終低于理論參考值。因此,可以認為動態跳頻序列具有較好的隨機性。
3.3 漢明相關性
漢明相關性分為漢明自相關和漢明互相關,它們表征了序列間的碰撞特性,反映了系統的抗衰落能力和用戶間組網的碰撞情況。周期為L的兩個序列在時延τ時的周期漢明相關定義為:
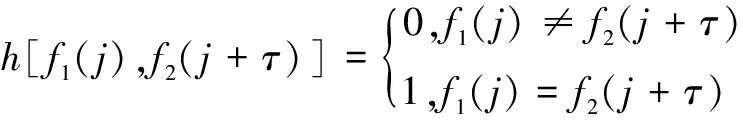
顯然,漢明相關值越小,漢明相關性越好。
漢明自相關及互相關仿真曲線分別如圖5、圖6所示。由圖5、圖6可知,動態跳頻序列的漢明自相關值和漢明互相關值都略微低于基于固定參數的頻率自適應跳頻序列的漢明自相關值和漢明互相關值。因此,可以認為動態跳頻序列具有更好的漢明相關性。

圖5 漢明自相關性仿真曲線
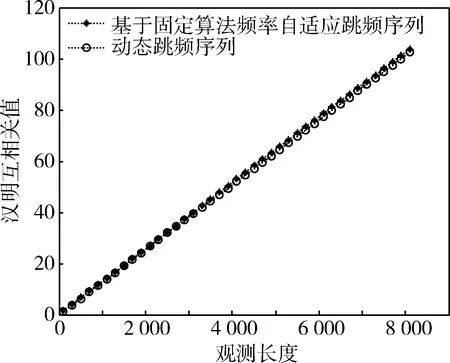
圖6 漢明互相關性仿真曲線
3.4 實時性
動態跳頻序列與常規跳頻序列的最大不同是頻率數可取任意值,且能根據感知環境實時變化。因此,圖7給出了頻率數分別為79、180、256、200時的時頻圖。由圖7可知,動態跳頻序列具有較好的實時性。
3.5 游程特性
跳頻序列中取值相同的相繼的(連在一起的)元素合稱為一個“游程”。在一個游程中元素的個數稱為游程長
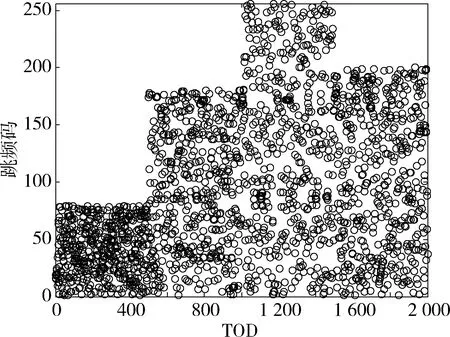
圖7 時頻圖
度,也就是在某個頻率上的停留時間。為了抗截獲和轉發式干擾,跳頻序列的最長游程越小越好。表2給出了完全隨機序列的不同游程長度的理論參考值和動態跳頻序列的檢測值。
由表2可知,動態跳頻序列的游程特性與理論參考值基本一致。因此,可以認為動態跳頻序列具有較好的游程特性。

表2 動態跳頻序列的游程特性
4 結論
針對現有跳頻序列的頻率數只能為素數的整數次冪的不足,本文基于m序列,利用非連續抽頭法,提出了一種頻率數可為任意值的跳頻序列。仿真結果表明,與基于固定參數的頻率自適應跳頻序列相比,本文提出的跳頻序列具有較好的均勻性、隨機性、漢明相關性等性能,同時,頻率數可為任意值,且能根據通信環境實時變化。
[1] 姚富強. 通信抗干擾工程與實踐(第二版)[M]. 北京: 電子工業出版社, 2012.
[2] 梅文華. 跳頻序列設計[M]. 北京: 國防工業出版社, 2016.
[3] 李偉, 禹思敏. 基于 Logistic 映射的混沌跳頻信號發生器設計與實現[J]. 微型機與應用, 2010,29(3): 44-48.
[4] 李思奇, 全厚德, 崔佩璋, 等. 基于混沌特性的跳頻序列復雜度分析[J]. 電子技術應用, 2013, 39(8): 113-116.
[5] 關磊. 高性能智能跳頻序列族構建與組網理論研究[D]. 西安:西安電子科技大學, 2015.
[6] 朱毅超, 陸建勛. 動態頻譜抗干擾系統在部分頻帶干擾下的性能[J]. 電子學報, 2011, 39(10): 2331-2337.
[7] 朱毅超, 梁亮, 田驊, 等. 一種基于認知的動態頻譜抗干擾新技術[J]. 通信技術, 2014, 47(1): 71-75.
[8] PARK S B, LEE K E, CHOI Y K, et al. Some good frequency hopping sequences with arbitrary number of slots[C].Military Communications Conference, MILCOM 2001, Communications for Network-Centric Operations: Creating the Information Force, IEEE, 2001, 2: 1325-1329.
[9] 李贊, 廖麗思, 金力軍, 等. 適用于任意頻隙數的跳頻序列族產生方法研究[J]. 無線電工程, 2004, 34(4): 1-3.
[10] 耿阿囡, 黃訓誠, 莊奕琪, 等. 一種任意頻隙跳頻序列構造方法[J]. 通信技術, 2007 (4): 54-56.
[11] Guan Lei, Li Zan, Xiao Song, et al. A family of adaptive frequency slot number FH sequences for high security and reliability communication[C].Intelligence and Security Informatics Conference (EISIC), 2015 European, IEEE, 2015: 30-36.
[12] 張邦寧,魏安全,郭道省. 通信抗干擾技術[M]. 北京: 機械工業出版社, 2006.
The research of frequency hopping sequences in dynamic spectrum anti-jamming systems
Li Shengnan1,2,Li Yonggui2,Yan Yan1
(1. College of Communication Engineering, PLA Uuniversity of Science and Technology, Nanjing 210007, China;2. Nanjing Telecommunication Technology Institute, Nanjing 210007, China)
Due to unbalanced integrated performance and fixed parameters, current frequency hopping (FH) sequences cannot be applied to dynamic spectrum anti-jamming system directly. Therefore, there is an urgent need to research a kind of dynamic FH sequence suitable for dynamic spectrum anti-jamming system. Based on m sequence, FH sequences, whose frequency slots number can be changed in real-time according to communication environment, was proposed. The simulation results show that, compared to the frequency adaptive FH sequence based on fixed parameters, the dynamic FH sequence has better performance in uniformity, randomness and Hamming correlation.
dynamic spectrum anti-jamming; frequency hopping sequences; arbitrary frequency slots number; uniformity
國家自然科學基金(61401505);江蘇省自然科學基金(BK20151450)
TN914.41
A
10.19358/j.issn.1674- 7720.2017.08.022
李勝男,李永貴,閆巖.動態頻譜抗干擾系統中跳頻序列研究[J].微型機與應用,2017,36(8):70-72,75.
2016-12-29)
李勝男(1993-),通信作者,女,碩士研究生,主要研究方向:無線通信、通信抗干擾。E-mail:18761685289@163.com。
李永貴(1964-),男,碩士,高級工程師,主要研究方向:通信抗干擾理論與技術。
閆巖(1992-),男,碩士研究生,主要研究方向:衛星通信、物理層安全。
________________________

