齊次邊界條件下圓柱殼的自由振動研究

汪志強，黃利華，李學斌

(武漢第二船舶設計研究所，湖北 武漢 430064)

齊次邊界條件下圓柱殼的自由振動研究

汪志強，黃利華，李學斌

(武漢第二船舶設計研究所，湖北 武漢 430064)

基于 Flügge 彈性薄殼理論研究圓柱殼在齊次邊界條件下的自由振動問題。圓柱殼的自振頻率通過位移控制方程和邊界條件控制方程聯立求解獲得。引入一般形式的位移函數之后，位移控制方程能夠得到關于頻率和波數的頻散圖，聯合邊界條件后轉化為 8 階矩陣行列式的零點求解。討論自振頻率點在頻散曲線中的位置，給出純虛數曲線分支的含義。還討論精確解和常用梁方法的聯系，研究振型在 3 個頻率區域變化的情況。

圓柱殼；自由振動；邊界條件；波傳播方法

0 引 言

圓柱殼結構在工程中得到了廣泛的應用，它的動態特性更是得到很多研究人員的持續關注[1]。對于圓柱殼的自由振動問題，通常的求解是基于位移方法，即根據圓柱殼的振動控制方程，引入一般位移表達式，然后再依據邊界約束獲得頻率。對于圓柱殼沿長度方向的位移表達形式大致可以分成兩類，即帶指數項的精確表達式[2]和其他近似表達式（如梁函數[3]、多項式[4]等）。近似表達式僅僅能夠滿足某些邊界條件，這種近似實際上會帶來誤差。

本文基于 Flügge 彈性薄殼理論[5]，給出了自由振動頻率和波數的精確解形式，并針對齊次邊界條件推導了控制方程。通過聯立振動控制方程和邊界約束方程獲得頻率之后，本文再進一步研究了邊界條件和頻散曲線之間的關系，找出了頻率-波數點在頻散曲線上的位置。對于面內 2 種振動（軸向為主、環向為主）對應的高階頻率也進行了探討。通過行列式曲線以及頻散曲線研究了截止（起始）頻率的 3 個區域，以及圓柱殼振動方式和這 3 個頻率段的關系。

1 理論分析

圖1 給出了本文討論的圓柱殼模型。殼體長度L，中面半徑R，厚度h。各向同性材料，彈性模量E，泊松比v，剪切模量G，密度ρ。殼體中面在坐標軸（x，φ，z）上位移分量分別為u，v和w（向內為正）。

基于 Flügge 彈性薄殼理論[5]，圓柱殼的自由振動方程可以表示為如下矩陣形式：

基于分離變量方法的思路，假設殼體振動的中面位移函數形式為：

式中：U0，V0和W0為振幅；λ為軸向波數；n為周向波數；ω為振動圓頻率（1/s）。將式（2）代入式（1），可以得到如下矩陣形式的控制方程：

其中方程（3）存在非零解的條件是系數行列式等于 0 ，即

式（4）即為圓柱殼自由振動的控制方程。該方程是關于圓柱殼幾何參數以及材料參數的特征方程。該方程是關于軸向波數λ的 8 次方程或者頻率ω的 6 次代數方程。

式中gi（i= 0，2，4，6，8），bj（j= 0，2，4，6）為方程的系數。

設定圓柱殼的幾何參數和材料參數，并假設環向振動波數n之后，方程（4）中未知數為軸向波數λ和頻率ω。

求解方程（5）可得到的 8 個精確解，這里簡寫為：

式中ai（i= 1～9）為參數。

方程（6）的 3 個根表示為：

式中ji（i= 1～5）為參數。

本文討論圓柱殼的齊次邊界條件，端部（x= 0，L）的邊界條件包括位移和轉角約束以及力、力矩約束[1]，即

將式（2）代入式（9）得到未知數軸向波數λ和頻率ω的邊界控制方程。

聯立邊界控制方程（9）和方程（4）就能求解齊次邊界下圓柱殼的振動頻率。先依據式（7）得到 8 個根，分別求出振型。

根據式（10）的振型，改寫式（2）的位移函數并代入邊界條件（9），可以得到一個關于Wi的 8 階齊次方程組

令系數矩陣A的行列式等于 0，則

求得頻率ω。

式（12）是一個關于頻率的超越方程。通常采用“掃頻”方式求解，即設定一定的頻率范圍，依照一定的頻率步長進行掃頻計算。

2 數值算例和討論

本文討論圓柱殼在齊次邊界條件下的自振特性，數值算例的基本參數是：L= 0.4 m，R= 0.1 m，h= 0.004 m，E= 2.11 × 1011N/m2，v= 0.3，考慮了 3 種典型的邊界條件[1]，即薄膜簡支 SD-SD（shear diaphragms），兩端固定 C-C（Clamped）和簡支-固定（SD-C）。定義無量綱的頻率參數為：

表1 給出了 3 種邊界下的頻率計算值。表中m為圓柱殼在軸向形成的振型半波數。

圓柱殼的兩端共有 8 個邊界條件，根據式（9）能夠組合成 136 種邊界[1]。依據本文給出的算法計算過程稍顯復雜，計算量也比較大。在分離變量的求解過程中，很多研究在軸向不采用指數項eλx而是采用更簡潔的一階或者多項式表達。在 1 階表達式中，最常用的就是梁的橫向振動形式，即把梁的邊界條件近似作為圓柱殼的邊界條件。

圓柱殼的邊界條件（9）是關于波數λ和頻率ω兩個未知量的方程。通過引入梁邊界方程進行簡化，式（9）就變成了僅僅關于波數λ的方程。這種簡化過程實際上也是波傳播方法的主要思路[6-7]。與表 1 中 3 種邊界條件對應，梁橫向振動的邊界條件和頻率方程見表 2[8]：

如果不考慮邊界條件式（9），方程（4）所表示的方程實際上就是圓柱殼的頻散方程[7]。當n= 2 時，波數λ和頻率參數Ω的圖形化顯示見圖 2。方程（4）有 8 個根，在圓柱殼的振動范圍，它們的形式為：

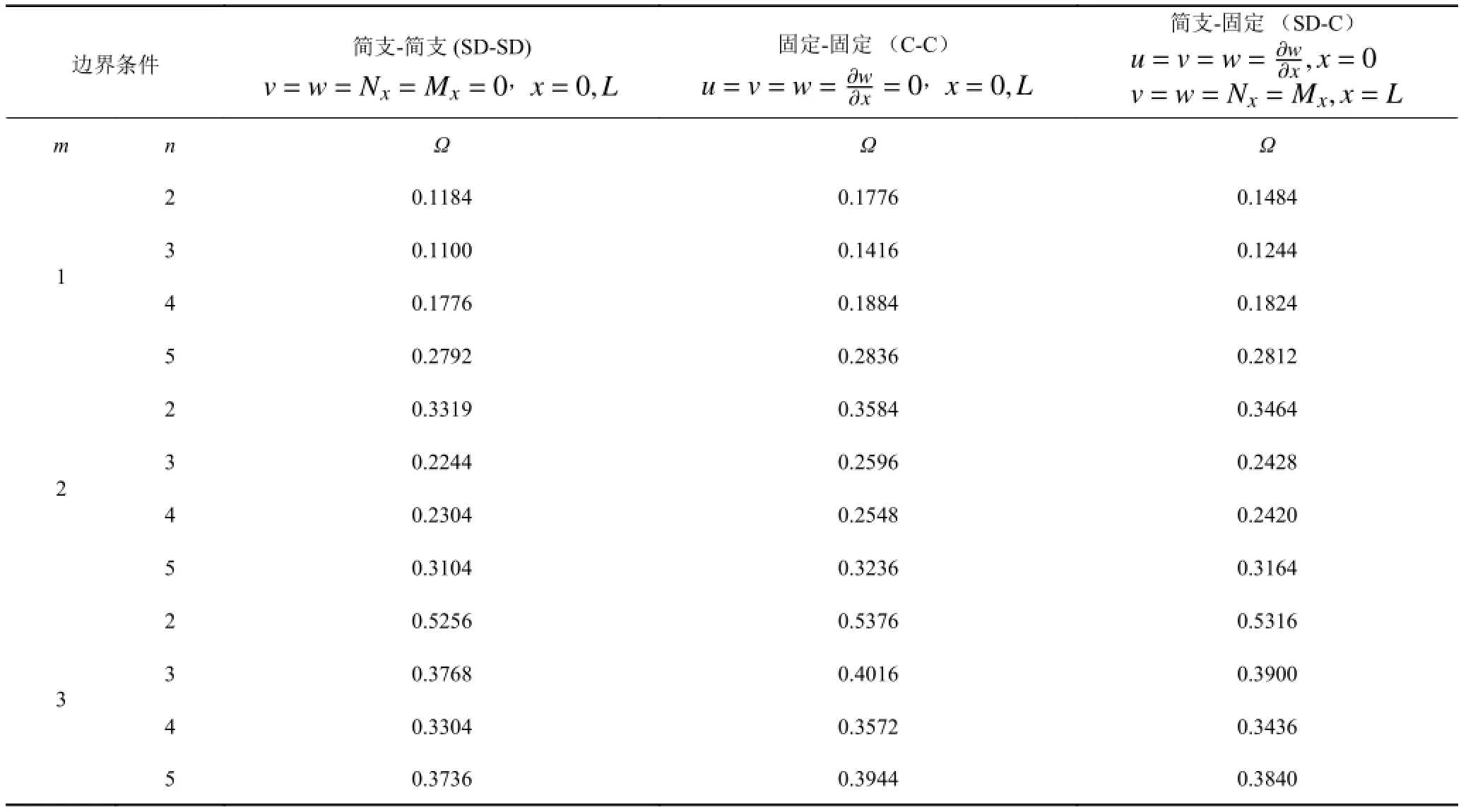
表1 3 種邊界下的頻率參數Ω計算值Tab. 1 Frequency parameters，Ωfor 3 boundary conditions

表2 梁的邊界條件和頻率方程Tab. 2 Characteristic equations and roots for beam vibration

其中，λ1,λ2,λ3,λ4都是正的實數。圖 2 給出了波數的實數、虛數以及復數形式的變化情況。根據頻率的范圍不同，這些根的形式和數量都會變化（文末 3D 圖能清晰看出）。（a）和（a）′分支曲線表示純虛數解，即其數值是 ±λ2。

從理論分析可知，圓柱殼的頻率是通過式（4）和式（9）聯立求解。對于式（4）添加邊界條件約束式（9），那么頻率點就會限定在這張圖的某條分支曲線上。以SD-SD邊界為例，對于m= 1，2，3，n= 2 時的 3 個頻率分別為 0.118 4，0.331 9 和 0.525 6（參見表 1）。這3 個頻率對應的純虛數解 |λ2| = 7.855 4，15.706 9 和 23.563 4。式（9）是一個關于頻率和波數的超越方程，難以圖形化表達。這里借用波傳播法的思路，即利用表 2 確定圓柱殼的頻率。對于SD-SD邊界，將波數表達式 λL=mπ 代入式（4）求解得到前 3 階頻率為0.118 4，0.331 9 和 0.525 6，與精確解相同。圖 3 給出了圖 2 的局部（下半部，|imag（λ）|＜30），并且在左側還給出了簡支邊界條件下梁的振型示意圖。考慮前3 階模態，從梁的橫向振型波數點λL=π,2π,3π可以得到對應的波數分別為 λBeam= 7.854 0，15.707 9和 23.561 9。通過梁的方法得到的 λBeam和圓柱殼的|λ2|非常接近。由此分析可知，圓柱殼的自振頻率點位于頻散圖純虛數那支曲線上（圖 2 的（a）,（a）’曲線）。從振動范圍考慮，其他波數解是方程（4）的增根。

以不同邊界下梁的波數節點畫水平線和頻散圖（a）曲線相交，就能夠得到圓柱殼的頻率，而這也正是波傳播法的求解思路。需要注意的是，這種用梁邊界代替圓柱殼的邊界會帶來誤差，例如，對于C-C邊界，類似的結果見圖 4。從圖 4 可以看出，連接梁的波數節點和圓柱殼的頻率點的線段已經不平行于橫軸。如果用平行線和圓柱殼的（a）分支相交（即波傳播方法），則得到的頻率就會有較大誤差。前 3 階模態基于梁邊界得到的波數 λBeam= 11.825，19.632 5 和27.490 0，而精確解得到的波數 |λ2| = 10.155 8，16.683 1和 24.130 7。采用波傳播方法，將 λBeam代入式（4）求解，得到的頻率分別為 0.223 6，0.434 7 和 0.603 0。這和精確解得到的頻率 0.177 6，0.358 4 和 0.537 6 已經有較大的誤差。誤差和結構的幾何參數以及振型（m，n）、邊界條件相關。經過大量的數值計算可以發現，邊界約束越強，圓柱殼越短，則波傳播方法的誤差也越大[7]。在圖形上看出，連接梁的波數節點和圓柱殼頻率點線段的斜率也越大。圖 4 的左上角還給出了梁振型函數的全貌。

對于SD-C邊界，前 3 階頻率為 0.148 4，0.346 4和 0.531 6，對應的純虛數 |λ2| = 9.053 9，16.238 7 和 23.845 3，沿著x方向的形狀是eiλ2的虛部，見圖 5。圖中還給出了對應梁的振動模態。從圖中可以看出，在SD端圓柱殼模型和梁模型相差不大，而在固定邊界處振型相差較大。

圖6 給出了純虛數λ2解隨頻率變化的情況。根據前述分析，自振頻率點位于頻散圖的純虛數分支上。對于頻率的求解，實際上式（6）在不同的頻率區間可以降冪。隨著頻率逐漸增大，這個方程的次數可以是2，4 或者 6 次。注意到，圖中波數為零時曲線和頻率軸有 3 個交點，對于n= 2，這 3 個頻率分別為 0.031 0，1.183 3 和 2.236 1。這 3 個點實際上是圓柱殼中傳播波的起始頻率 ?cut?on，也是對應虛數波的截止頻率。這些頻率隨幾何參數以及模態變化。圖 7 給出了不同n值時的純虛數曲線。

當波數為 0 ，3 個起始頻率通過式（8）和式（13）可以得到：

圖6和圖7 還可以和長度待定方法聯系起來使用。即給定一個頻率（大于第 1 個起始頻率），總能夠找到與之對應的至少 2 個波數 λ（負數舍去），聯合邊界條件（參考圖 3 或者圖 4），由此波數可以求解得到殼體的長度。這其實就是長度待定方法的求解過程[10]，這種方法能夠用于圓柱殼的動力設計。

本文是利用系數矩陣行列式進行邊界條件的計算并判斷頻率點。式（12）中A是一個復數矩陣。在實際的計算中，A的行列式并不真正等于 0。通常使用行列式的模值進行頻率點的判斷。在掃頻過程中，模值曲線會出現很多的局部極小值點。對于這些極小點的數值需要仔細甄別。由于起始（截止）頻率的存在，低于首個起始頻率的點都不會是圓柱殼的自振頻率。圖 8 給出了一個SD-SD邊界算例。當n= 8 時，模值曲線前 2 個極小值點用P1和P2表示，從頻散圖可以看出，P1點對應于 8 個復數解向實數、虛數解和復數解過渡，而P2點就對應首個起始頻率，Ωp2= 0.902 2。從這個過程還可以看出，P1和P2點是和圓柱殼的邊界條件無關的，它只取決于殼體的幾何（不含邊界）與材料參數。

SD-SD邊界的近似梁函數表示中，經常使用三角函數近似表示軸向位移，式（4）就是關于頻率Ω2的 3 次方程。根據振型判斷，最低頻率、中間頻率和最高頻率分別對應著徑向位移分量w最大、軸向位移分量u最大、切向位移最大v而其他 2 個方向位移較小的運動[11]。本文使用的精確解解過程也能夠計算對應軸向位移分量u和切向位移分量v為主的圓柱殼頻率。在圖 6和圖7 中，第 2 個和第 3 個起始頻率之后的純虛數分支，就分別代表了軸向位移u和切向位移v對應的較高頻率分布。結合圖 3 和圖 6 的思路，可以求解這 2 種較高階頻率。仍舊以SD-SD邊界為例，圖 9給出了這樣的計算過程。從梁的振型結點過來的連接線（平行）對應共有 9 個頻率點，這些點反映在系數矩陣行列式曲線上的情況如圖 10 所示。

從圖 10可看出，第1階起始頻率為 0.031，遠小于環頻率（Ωring= 1）。在 [0.031，1] 頻率區間有很多的頻率點，它們對應于徑向w為主的振型。軸向位移u為主的頻率出現在第 2 個起始頻率之后，切向位移v為主的頻率則出現在第 3 個起始頻率之后。圖中依照起始頻率給出了 3 個頻率范圍（Ⅰ 區, Ⅱ 區和 Ⅲ區）。在 Ⅰ 區只有（a）分支，即這個區域內的振動均是對應徑向位移較大的情況，這也就是通常圓柱殼振動考慮的范圍（Ω＜1）。在區域 Ⅱ 內，存在 2 條曲線（a）和（b），因此，會出現軸向位移u比較大的振型（曲線（b）），如m= 1，2，3 的軸向振型，也會出現高階對應徑向位移w為主的振型（曲線（a）），例如m= 14 時，對應的 3 個頻率是 1.707 2，6.616 6 和11.181 3。在 Ⅲ 區域里，則 3 種振型會并存。圖中除了給出切向v為主的前3階頻率點，也給出了m= 18 時徑向振動為主以及m= 6 時軸向振動為主的頻率點。

為了更好理解頻散圖形對于求解頻率的理解，本文還給出了方程（4）的三維圖形。從圖中能夠清晰看出 8 個波數隨頻率的變化情況。

3 結 語

本文采用精確解方法研究圓柱殼的自由振動頻率特性。可以得到如下結論：

1）圓柱殼的所有齊次邊界條件的頻率點都存在于頻散曲線中的純虛數分支上。對于振動而言，根據研究的頻率范圍，頻散曲線可以退化為 2，4 或者 6 次方程。

2）精確解方法能夠求解對應的以軸向位移和切向位移為主的頻率，它們和高階徑向為主的頻率交叉在一起。

3）圓柱殼自振存在著最低的起始頻率，這個頻率點對應于無限長圓柱殼的頻率。加上邊界約束之后的頻率均高于該起始頻率。

4）通常采用的梁橫向振動振型和波傳播法得到的頻率均存在誤差。其中SD-SD的誤差非常小，可以忽略。邊界約束越強，殼體越短，則誤差越大。

[ 1 ]LEISSA A W. Vibration of Shells (NASA SP 288)[R]., 1993.

[ 2 ]FORSBERG K. Influence of boundary conditions on the modal characteristics of thin cylindrical shells[Z]. 1964: 2.

[ 3 ]DAI L, YANG T, DU J, et al. An exact series solution for the vibration analysis of cylindrical shells with arbitrary boundary conditions[J]. Applied Acoustics. 2013, 74: 440-449.

[ 4 ]SHARMA C B. Free vibrations of clamped-free circular cylinders[J]. Thin-Walled Structures. 1984, 2(1): 175-193.

[ 5 ]FLUGGE. Stresses in shells[M]. Springer: 1973.

[ 6 ]ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration. 2001, 239(3): 397-403.

[ 7 ]XUEBIN L. Study on free vibration analysis of circular cylindrical shells using wave propagation[J]. Journal of Sound and Vibration. 2008, 311: 667-682.

[ 8 ]方同, 薛璞. 振動理論及應用[M]. 西安: 西北工業大學出版社, 1998.

[ 9 ]陳正翔, 江松青, 張維衡. 圓柱殼中結構振動波的傳播特性[J]. 振動工程學報. 1998, 11(4): 450-456. CHEN Zheng-xiang JIANG Song-qing ZHANG Wei-heng. Dispersion characteristics of structure vibration waves in cylindrical shells[J].Journal of Vibration Engineering. 1998, 11(4): 450-456.

[10]WARBURTON G B. Vibration of thin cylindrical shells[Z]. 1965: 7, 399-407.

[11]ARNOLD R N, WARBURTION G B. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends[Z]. 1949: 197.

Vibration analysis of circular cylindrical shells under arbitrary boundary conditions

WANG Zhi-qiang, HUANG Li-hua, LI Xue-bin
(Wuhan Second Ship Design and Research Institute, Wuhan 430064, China)

The study of circular cylindrical shells under arbitrary boundary conditions is provided, based on Flügge thin shell theory. The frequency can be obtained from motion control equations and boundary condition equations. An exact displacement expression is used for analysis. The sweep frequency skill is utilized for finding the roots of corresponding equation which derived from those two characteristic equations. The zeros of this equation are the frequencies of shells depending on specific boundaries in both ends. The dispersions plots of shells are studied together with boundary conditions. From the analysis, the frequency-wave points are located on the purely imaginary part of dispersion plot for arbitrary boundary conditions. The main procedure of wave propagation approach is also discussed for vibrations of shells. The total frequency domain could be divided into 3 parts, which corresponding to 3 vibration types of shells. Numerical examples are provided in this paper for demonstration of present analysis procedure.

circular cylindrical shells；free vibration；boundary conditions；wave propagation approach

U661.44

A

1672 - 7619(2017)04 - 0024 - 06

10.3404/j.issn.1672 - 7619.2017.04.005

2016 - 06 - 03；

2016 - 07 - 04

汪志強(1990 - )，男，碩士研究生，研究方向為潛艇結構振動及結構優化。