縱骨對環肋圓柱殼肋間殼板穩定性的影響
王小明
(中國艦船研究設計中心,湖北 武漢 430064)
縱骨對環肋圓柱殼肋間殼板穩定性的影響
王小明
(中國艦船研究設計中心,湖北 武漢 430064)
肋間殼板失穩是潛艇耐壓殼體失穩的重要形式之一,加設縱骨是提高環肋圓柱殼肋間殼板穩定性的有效方法。通過理論計算,得出以下結論:加設縱骨可以提高環肋圓柱殼肋間殼板穩定性,且α值越大,效果越明顯;加設縱骨后的環肋圓柱殼在肋間殼板失穩時,縱向失穩半波數等于 1,周向失穩波數大于 10,且縱骨尺寸越大,周向失穩波數越大;失穩臨界壓力隨肋距的減小而增大,隨縱骨尺寸的增加而增大。
環肋圓柱殼;殼板穩定性;失穩臨界壓力
0 引 言
在研究環肋圓柱殼總穩定性過程中,有的研究學者認為,當肋骨尺寸增大到一定程度后,繼續增大肋骨尺寸,并不能顯著提高圓柱殼的總穩定性,而增設縱骨才能有效提高其總穩定性[1-4]。進一步的研究還表明[4-5],在通常情況下,加設縱骨對圓柱殼總穩定的影響不明顯,只有在殼體短、殼板薄、直徑大的情況下才有效。加設縱骨對通常情況下的圓柱殼總穩定性影響不明顯,未必對肋間殼板穩定性也影響不明顯。有研究表明[6],通常情況下,加設縱骨可能是提高殼板穩定性更好的方法,因此需要深入研究縱骨對環肋圓柱殼肋間殼板穩定性的影響。
1 肋間殼板穩定性計算公式
用能量法可以推導出環肋圓柱殼在軸向和橫向壓力聯合作用下的總穩定性方程[7]:
式中符號含義與文獻[7]相同。
根據文獻[5]的結論可以導出縱橫加筋圓柱殼在軸向和橫向壓力聯合作用下的總穩定性方程:
式中:J為計及帶板的縱骨慣性矩;b為縱骨間距。
參考文獻[8],類似推導公式。可以求得,僅受軸向均勻壓力作用下,環肋圓柱殼肋間殼板失穩臨界壓力公式和縱橫加筋圓柱殼肋間殼板失穩臨界壓力公式為:
僅受橫向均勻壓力作用下,環肋圓柱殼肋間殼板失穩臨界壓力公式和縱橫加筋圓柱殼肋間殼板失穩臨界壓力公式為:
向均勻壓力作用下,環肋圓柱殼肋間殼板失穩臨界壓力公式和縱橫加筋圓柱殼肋間殼板失穩臨界壓力公式為:
引入參數 γ=100t/R,η=106J/(R3b),則式(5)~式(10)都可以用 γ 和 η 表達,此處僅列出式(9)和式(10)的表達式,其余可作類似推導。
2 縱向失穩半波數和周向失穩波數的變化
取 10≤α≤20,并在 α 取值范圍內取一系列的離散值,計算式(9)中的縱向失穩半波數m和周向失穩波數n,計算結果如表 1 所示。
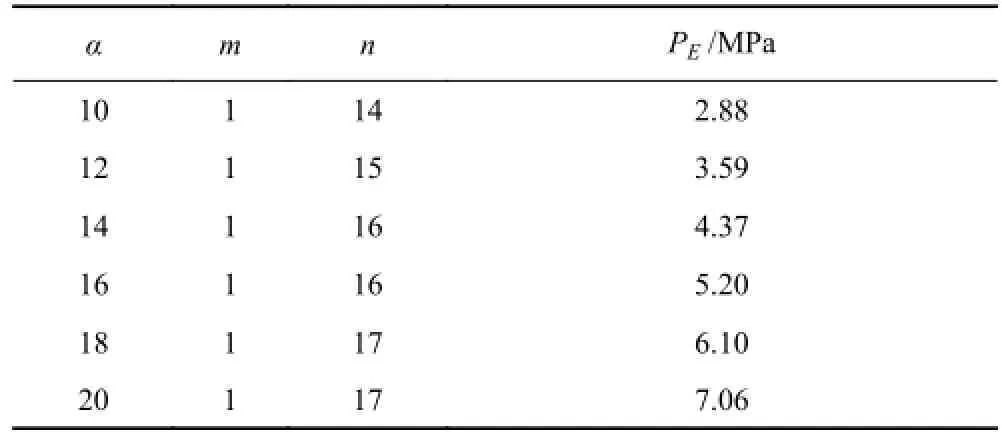
表1 環肋圓柱殼的m和n值Tab. 1mandnvalue for the ring-stiffened cylindrical shell
對式(10)中的 α 取上述一樣的離散值,η 則在1≤η≤10內取離散值,分別計算式(10)的縱向失穩波數m和周向失穩波數n,計算結果列于表 2。
從表 1 可看出,環肋圓柱殼殼板失穩時,縱向失穩半波數m= 1,周向失穩波數n>10,且隨著 α 值的增大而緩慢增大。從表 2 則可看出,縱橫加筋圓柱殼肋間殼板失穩縱向失穩半波數m= 1,周向失穩波數n>10,但隨著 α 或 η 值的增大而迅速增大。

表2 縱橫加筋圓柱殼的m和n值Tab. 2mandnvalue for the longitudinal and transverse stiffened cylindrical shell
3 肋間殼板失穩臨界壓力曲線圖
根據式(9)、式(10)和相應式(3)~式(6)的變換式,編制計算機程序,可以繪制環肋圓柱殼肋間殼板失穩臨界壓力PE與 α 的曲線PE-α 曲線和縱橫加筋圓柱殼肋間殼板失穩臨界壓力曲線PEL-α 曲線、PEL-η 曲線。相應的僅軸向受壓肋間殼板失穩臨界壓力曲線和與僅橫向受壓肋間殼板失穩臨界壓力曲線和也一同繪制在相應的圖中。
圖1為PE-α 曲線、曲線和曲線。
圖2 是 η=1,3,5,7,9 時的PEL-α 曲線,曲線和曲線。
圖2 是 α=10,12,14,16,18,20 時的PEL-η 曲線、曲線和曲線。
由圖 1 可看出,PE隨 α 的增大而增大,即PE隨肋距l的減小而增大。α<21 時,若 α>21,則
由圖 2 得知,同樣隨 α 的增大而增大,η 越大則增長率越快。
圖3 表明,和PEL幾乎都是隨 η 線性增加,增長率很大,明顯大于的增長率;與基本相同,數值也非常接近。α 增大,PEL的增長率亦增大。η 取值越大,PEL與差距也越大,這意味著縱橫加筋圓柱殼的肋間殼板穩定性取決于其橫向剛度。加設縱骨后,圓柱殼的縱向剛度明顯提高,縱向穩定性則提高,表現為顯著提高;相對于縱向剛度而言,加設縱骨對橫向高度的提高作用非常有限,所以,增大縱骨規格或減小縱骨間距,即增大 η,增加不明顯。
將圖 1 與圖 2 ~ 圖 3 比較可以發現,環肋圓柱殼加縱骨后,其肋間殼板穩定性明顯提高。這一點也可以從表 1 和表 2 的對比中得到印證。以 α=10 為例,η = 1提高 171%,η = 3 則提高 349%……η 值越大,提高百分率越大。同樣,縱骨尺寸不變,間距不變,即 η 不變,α 變大則臨界壓力提高百分率也增大。
4 有限元計算驗證
式(7)或式(9)已經是成熟可靠的公式,不必做有限元計算驗證。縱橫加筋圓柱殼肋間殼板失穩臨界壓力計算式(8)或式(10)則處于研究討論階段,公式本身的準確性和上述計算方法的準確性尚不明確,需要用有限元計算來驗證。
根據第3節中的基本數據,α=10,η分別取 1, 3,5,7 和 9,建立有限元模型。圓柱殼殼板采用曲殼單元,縱骨則采用梁單元。邊界條件是兩端節點都約束徑向位移和周向位移,其中一端除此外,還要約束軸向位移;載荷為在未施加軸向位移約束的一端施加線載荷,殼面上施加面載荷。
邊界條件:
計算中均勻外壓p=1Pa,直接施加于柱殼幾何面上,而施加于z=l位置的圓周線上的載荷為pR/2。
有限元計算結果列于表 3。

表3 失穩臨界壓力計算結果對比Tab. 3 Lose stability critical pressure calculation result contrast
從表 3 的對比可看出,公式計算的誤差在 15% 范圍以內,具有一定的可靠性。
5 結 語
1)環肋圓柱殼肋間殼板失穩時,縱向失穩半波數m= 1,周向失穩波數n>10。加設縱骨后成為縱橫加筋圓柱殼,肋間失穩時,縱向失穩波數m= 1,周向失穩波數n>10,且n比環肋圓柱殼的大。縱骨尺寸越大,即 η 越大,則n越大。
2)環肋圓柱殼失穩臨界壓力PE隨著肋距 l 的減小(α 的增大)而增大。僅縱向受壓時,肋間殼板失穩臨界壓力在 α 增大過程中,先保持不變,當 α 增大到 21 以后,其數值開始逐漸增大。
3)縱橫加筋圓柱殼肋間失穩臨界壓力PEL隨肋距的減小(α 的增大)而增大。當 α 保持固定時,臨界壓力PEL隨縱骨尺寸的增大,間距的減小(η 的增大)而增加,且 η 越大,失穩臨界壓力越取決于圓柱殼的橫向剛度。
4)環肋圓柱殼加設縱骨后,其肋間失穩臨界壓力明顯提高,α 越大的情況下,其提高的效果越明顯。這種提高更表現在加與不加縱骨,加縱骨則肋間殼板失穩臨界壓力立刻升高,這一點表現出與環肋圓柱殼總穩定性相同的性質;不同的是肋間殼板失穩臨界壓力隨 η 的增大持續緩慢增大,而總失穩臨界壓力則隨η的增大先增大,在增大到一個定值后保持不變。
5)式(8)或式(10)計算結果與有限元計算結果相比,誤差在 15% 以內,數據的變化趨勢二者相同。
[1]王曉天, 鄧劍平, 寧林, 等. 環肋圓柱殼穩定特性與破壞模式的探討[J]. 哈爾濱工程大學學報, 1997(6): 13-21. WANG Xiao-tian, DENG Jian-ping, NING Lin, et al. A study of the stability features and bulking pattern of the ring-stiffened cylindrical shell[J]. Journal of Harbin Engineering University, 1997(6): 13-21.
[2]謝祚水. 許輯平. 潛艇薄壁大半徑圓柱殼的總穩定性[J]. 中國造船, 1994(2): 82-88. XIE Zuo-shui. XU Ji-ping. On the overall stability of submarine circular cylindrical shells with large diameters and thin thicknesses [J]. Shipbuilding of China, 1994(2): 82-88.
[3]謝祚水. 環肋圓柱殼穩定特性研究[J]. 中國造船, 1998(4):73-80. XIE Zuo-shui. Stability study of ring-stiffened circular cylindrical shell [J]. Shipbuilding of China, 1998(4): 73-80.
[4]王林, 謝祚水. 縱橫加肋耐壓圓柱殼結構穩定性[J]. 造船技術, 1998(12): 23-25. WANG Lin, XIE Zuo-shui. Stability of longitudinal and transverse stiffened cylindrical shell structure[J]. Technology of Shipbuilding, 1998(2): 23-25.
[5]謝祚水. 受均勻外壓力作用的圓柱殼結構形式的初步探討[J].鎮江船舶學院學報, 1990, 4(4): 31-37. XIE Zuo-shui. Preliminary study of structure type of circular cylindrical shell under uniform external pressure [J]. Journal of Zhenjiang Shipbuilding Institute, 1990, 4(4): 31-37.
[6]謝祚水. 王志軍. 潛艇耐壓圓柱殼結構的優化設計[J]. 中國造船, 1993(12): 23-25. XIE Zuo-shui. WANG Zhi-jun. Optimum design of circle cylindrical pressure shell for submarine[J]. Shipbuilding of China. 1993, (12): 23-25.
[7]許輯平. 潛艇強度[M]. 北京: 國防工業出版社.1980. XU Ji-ping. Strength of Submarine[M]. Beijing: National Defense Industry Press, 1980.
[8]王小明. 肋距對環肋圓柱殼殼板穩定性的影響[J]. 中國艦船研究, 2013, 8(6): 81-84. WANG Xiao-ming. The influence of frame interval on the stability of ring-stiffened cylindrical shells[J]. Journal of Ship Research, 2013, 8(6): 81-84.
Longitudinals influence on stability of shell between ribs for ring-stiffened cylindrical shell
WANG Xiao-ming
(China Ship Development and Design Center, Wuhan 430064, China)
Losing stability of shell between ribs is one of important form for submarine pressure hull. To improve the stability of shell between ribs for cylindrical shell, adding longitudials is a effective way. The following conclusion is gotten by theoretical calculation. Adding longitudinals improves the stability of shell between ribs for the ring-stiffened cylindrical shell whose longitudinal losing stability semi-wave number is equal 1, and circular losing stability wave number is more than 10.,the more value of α, the more obvious effect. Circular losing stability wave number increases with increasing longitudinals size, and losing stability critical pressure increases with decreasing of rib distance and increasing longitudinals size.
ring-stiffened cylindrical shell;stability of shell;losing stability critical pressure
U663.1
A
1672 - 7619(2017)04 - 0035 - 05
10.3404/j.issn.1672 - 7619.2017.04.007
2016 - 03 - 02;
2016 - 07 - 29
王小明(1981 - ),男,工程師,從事船舶結構設計與研究工作。

