含初始撓度加筋板的穩定性分析

劉春正，吳 梵，牟金磊

(海軍工程大學 艦船工程系，湖北 武漢 430033)

含初始撓度加筋板的穩定性分析

劉春正，吳 梵，牟金磊

(海軍工程大學 艦船工程系，湖北 武漢 430033)

為了確定初始撓度變形對加筋板穩定性的影響作用，根據實際情況假設初始撓度為雙三角級數形式，利用 Ansys 計算分析了整體初始撓度的幅值與半波數對彈性失穩壓力的影響，并得到初始撓度對加筋板穩定性的影響因子計算方法。計算結果分析表明，隨著初始撓度的幅值和半波數的增加，加筋板彈性失穩壓力逐漸減小；對于含有某種初始撓度的加筋板，其影響因子主要受加筋板的厚度和加強筋間距的影響，而加筋板長寬比的影響較小，可以忽略。

初始撓度；加筋板；穩定性；幅值；半波數；影響因子

0 引 言

加筋板被廣泛應用于許多工程結構中，它大大提高了板的承載能力。在加筋板的設計中，加筋板的穩定性是一個必須考慮的重要因素，同時由于加筋板穩定性問題的復雜性，對加筋板穩定性的研究顯得尤為重要[1]。加筋板結構為船體甲板結構的基本構件，其穩定性直接影響整體結構的承載能力。艦船在中垂狀態時甲板板架受總縱彎曲軸向壓力，甲板板架是距離中和軸最遠的主船體受壓結構，所受的軸向壓力最大，只有保證甲板的穩定性，才能保證艦船整體結構的穩定性[2]。加筋板作為船體甲板的主要結構單元，研究其穩定性十分必要。船用加筋板結構屈曲行為一般分為板的屈曲、加強筋屈曲、加強筋之間的板格屈曲和加筋板格的整體屈曲 4 種[3-4]。其中加筋板的整體屈曲是最危險的屈曲情況。

加筋板結構在長期使用過程中，由于各種載荷的作用，會產生固定的初始撓度變形。初始撓度變形對加筋板的穩定性和極限承載能力都會產生嚴重不利影響。因此，在加筋板的穩定性分析中，考慮初始變形等因素的影響，具有重要的工程意義。

目前，國內考慮初始撓度變形對結構穩定性影響的研究較多。但研究初始撓度的具體形式對加筋板穩定性影響較少；而且對船用加筋板初始撓度的考慮都是基于船體結構建造時的測量的數據，并未考慮艦船長期服役之后產生的撓度變形的具體情況以及其對加筋板穩定性產生的影響。本文主要考慮艦船長期服役之后，加筋板的整體撓度變形情況對其穩定性的影響。假設初始撓度為雙級數形式，利用有限元方法計算含初始撓度加筋板的彈性失穩壓力。并通過控制初始撓度函數形式，討論初始撓度的幅值與半波數對彈性失穩壓力的影響，最后得到初始撓度對加筋板穩定性的影響因子。

1 含初始撓度加筋板的穩定性分析

1.1 有限元模型建立

本文根據某艦船的甲板結構，選取甲板典型位置處的某一加筋板作為研究對象。該加筋板具有 6 條縱向加強筋，板尺寸a×b為 1 500 mm × 2 800 mm，加強筋間距s= 400 mm，加強筋均為角鋼，角鋼尺寸為

研究中，利用有限元分析軟件 Ansys，根據加筋板的具體尺寸，建立合適的有限元模型。采用 shell181單元，單元長度在 20～30 mm 之間，計算中假定板的材料是理想彈塑性，彈性模量E= 2.1 × 105MPa，泊松比ν= 0.3。

加筋板的邊界條件定義為四邊簡支，具體定義方法可以參照相關文獻[5]：

1）加筋板的四周邊界限制法向位移Uz= 0，即為z方向簡支；

2）長度方向兩端AB，CD邊（x= 0 和x=a處）限制轉角位移Rx=Rz= 0，即可沿y方向自由轉動；寬度方向兩端AD，BC邊（y= 0 和y=b處）限制轉角位移Ry=Rz= 0，即可沿x方向自由轉動；

3）AB，CD邊線保持沿x方向的直邊約束，AD，BC邊線保持沿y方向的直邊約束；

4）AB、CD邊線中點限制y方向位移，即Uy= 0，AD、BC邊線中點限制x方向位移，即Ux= 0。

加筋板的外載荷施加方式為在AB，CD兩端截面同時施加軸向壓力為 1 MPa 的集中力載荷，在有限元軟件中轉換施加到截面節點上。有限元模型的邊界條件和載荷施加情況如圖 1 所示。

1.2 初始撓度設計

初始撓度這種結構上的缺陷可分為整體和局部 2種形態。整體初始撓度是指板和加強筋同時產生撓度變形；局部初始撓度是指僅板產生的撓度變形。初始撓度形態主要包括兩方面因素，即幅值和半波數。在較長的跨度范圍內，初始撓度是由多個半波所組成的曲面，而在較短的范圍內（ 2 個加強筋之間）一般只有一個半波。船體加筋板初始撓度形態可以看成由多種半波形式疊加而成，可用如下公式表示：

也有用如下公式來表示焊接作用導致加筋板產生的撓度變形[6]：

式中：w0為初始撓度，mm；wopl為加強筋間板格的最大初始撓度，mm；Boi為初始變形幅值，mm。

加筋板結構的一階屈曲模態是最容易產生的失穩狀態，對加筋板的穩定性有重要影響[7]。一般認為，取一階模態作為結構的初始缺陷比較合理。本文在考慮初始撓度時，并不是考慮焊接影響產生的撓度變形，而是考慮長期外載荷作用下產生的撓度變形，這種撓度變形在加載之前就已經存在，故稱為初始撓度。根據艦船甲板實際情況，可以假設初始撓度用下式表示：

考慮半波數對彈性失穩壓力的影響時，限定y方向為一個半波，只考慮x方向半波數的影響。

本文擬采用式（3）的初始撓度形式模擬實際初始撓度情況，來研究整體初始撓度的幅值和半波數對加筋板彈性失穩壓力的影響。

根據船廠生產實踐和調研結果，當強力甲板厚度在 7～10 mm 之間時，鋼板的絕對變形量達到 35 mm時，才會對鋼板進行矯正修復；從對我國甲板變形測量的數據統計來看，甲板變形一般在 8 mm 左右。為了使研究更具有實用性，本文將初始撓度幅值設定在0～30 mm 之間進行計算研究。國內關于艦船甲板板架變形的半波數測量研究內容較少。國外有對船廠建造中船體變形情況測量的研究[8]，初始撓度的半波數一般在 3 個以內。本文根據施加初始撓度的實際情況，決定最多取 6 個半波作為研究對象。

1.3 初始撓度對彈性失穩壓力的影響

在有限元軟件 Ansys 中，可以通過對各個節點施加具體的法向位移來實現初始撓度的設計與施加。圖 2所示為具有 1 mm 幅值、一個半波初始撓度的加筋板。

當計算模型不具有初始撓度時，計算所得彈性失穩壓力為 333.012 MPa。通過不斷改變初始撓度的幅值和半波數，計算相應的彈性失穩壓力數值，計算數據見表 1。

1.3.1 初始撓度幅值對加筋板彈性失穩壓力的影響

根據計算數據可以繪制出彈性失穩壓力與初始撓度幅值的關系圖，從而可以判定，在某一半波數情況下，彈性失穩壓力隨初始撓度幅值的變化規律。為了更加方便比較不同半波數的初始撓度情況下，彈性失穩壓力隨幅值的變化規律，將各個半波數下的曲線繪制到同一個坐標系下，并考慮將初始撓度幅值和彈性失穩壓力轉化為無因次量，取初始撓度幅值f與加筋板厚度t的比值為自變量，取含初始撓度加筋板彈性失穩壓力σ與不含初始撓度加筋板彈性失穩壓力σcr比值作為因變量，如圖 3 所示。

從圖中可看出，曲線整體呈現半波數越大，彈性失穩壓力的變化率越大的規律。在幅值較小的一定范圍內，含初始撓度加筋板彈性失穩壓力大于不含初始撓度加筋板的彈性失穩壓力，該范圍即可以稱為有利范圍；超過一定范圍，彈性失穩壓力小于原來的彈性失穩壓力。

1.3.2 初始撓度半波數對加筋板彈性失穩壓力的影響

由于計算數據較多，考慮初始撓度半波數對彈性失穩壓力的影響，只選取了含幅值為 5 mm，10 mm，15 mm，20 mm，25 mm 和 30 mm 初始撓度的數據進行分析，如圖 4所示。

圖4 顯示了當初始撓度幅值不變時，增加初始撓度的半波數，加筋板的彈性失穩壓力的變化情況。從圖中可以清晰地看出，不同的初始撓度情況下，彈性失穩壓力整體的變化規律相似，都是隨著半波數的增加而減小。在半波數不超過 3 的情況下，彈性失穩壓力的變化率隨半波數增大逐漸增大，當初始撓度幅值越大，彈性失穩壓力隨半波數的變化率也增大；半波數大于 3 的情況下，彈性失穩壓力變化率減小。當半波數為 4 時，彈性失穩壓力會突然變大，但是這種作用隨著初始撓度幅值的增大而逐漸減小并消失。

2 初始撓度影響因子確定

由計算可知，含初始撓度的加筋板的彈性失穩壓力與不含初始撓度加筋板的值存在一定差距。后者與前者差值反映了初始撓度對加筋板彈性失穩壓力的影響，定義兩者差值與后者的比值為影響因子 φ，即

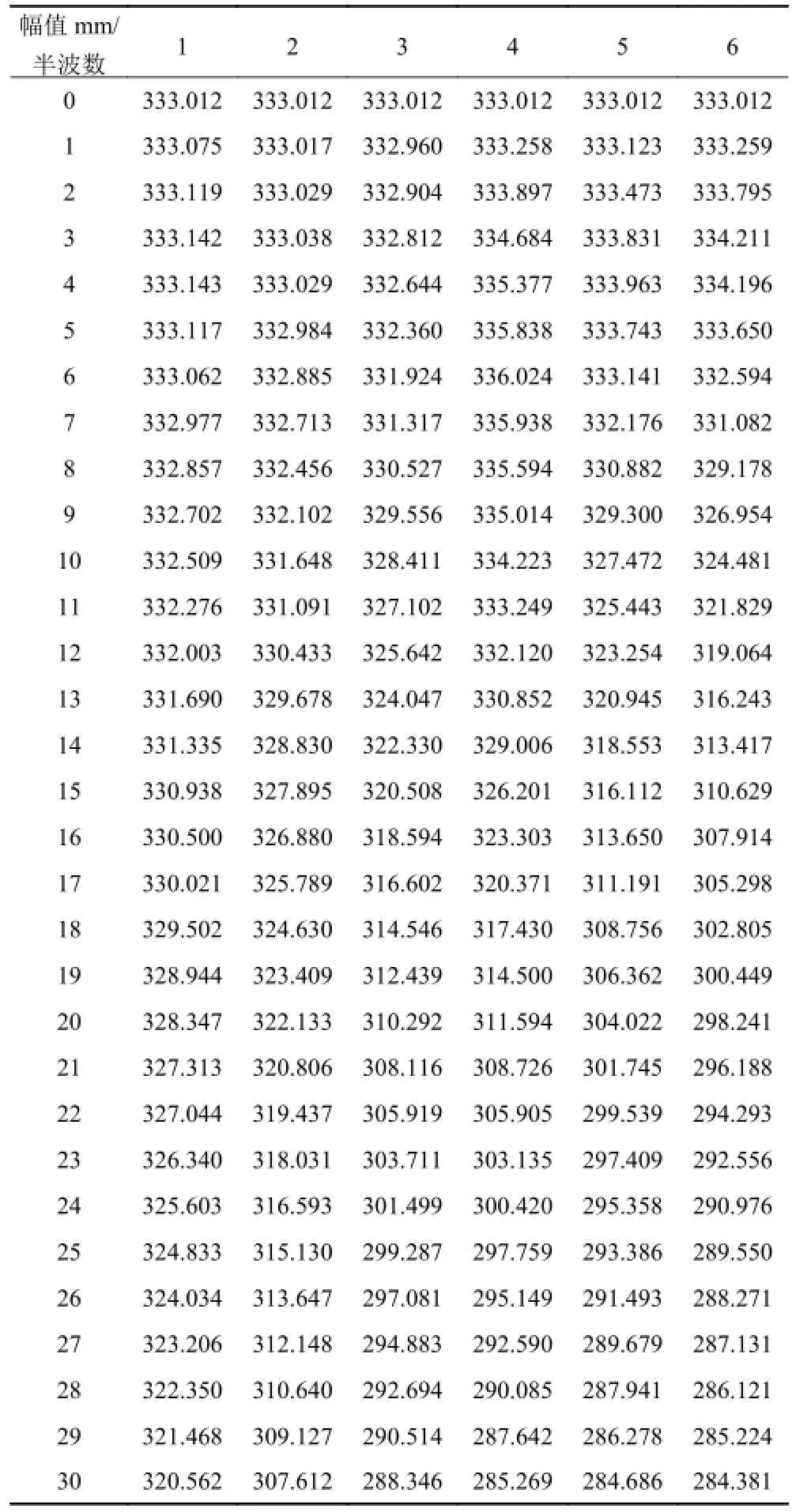
表1 含不同初始撓度加筋板的彈性失穩壓力（MPa）Tab. 1Pof the stiffened plate with different initial deflections（MPa）

相關文獻已經對含有初始缺陷的加肋圓柱殼理論失穩壓力的修正系數進行了研究[9-10]，參考其研究內容，可以初步確定影響因子與加筋板的長寬比、板厚、加強筋間距等幾何尺寸有關。下面將分析含初始撓度加筋板彈性失穩壓力與各主要尺寸參數的關系，計算模型是利用第 2 節的有限元模型作為基礎，進行相應的參數改變。根據對中修船體甲板變形的勘驗測量數據可知，船體加筋板出現的初始撓度幅值大部分在 10 mm 左右，具有 1 個半波形式，因此只討論含有幅值 10 mm、具有 1 個半波初始撓度的加筋板的影響因子。

2.1 加筋板長寬比與影響因子的關系

根據相關對船體加筋板尺寸的統計數據[11]，船體加筋板板長a與加強筋間距s的比值應該滿足關系：2≤a/s≤6。因此，控制加強筋間距保持不變，主要通過改變加筋板的長度a來改變加筋板的長寬比a/b。

已知加筋板計算模型加強筋間距s=400 mm ，具有 6 根加強筋，加筋板寬度b= 2 800 mm 所以加筋板長度取值范圍為 800≤a≤2 400，均勻取值：800 mm，1 000 mm，1 200 mm，1 400 mm，1 600 mm，1 800 mm，2 000 mm，2 200 mm，2 400 mm。經過計算可以得到影響因子如表 2。可以將表 2 數據放在直角坐標系中顯示，如圖 5 所示。

從圖 5 中可以看出，隨著加筋板長寬比 a/b 的變化，影響因子 φ 的數值都出處在 0.996 到 1 的范圍之內，且變化趨勢趨于平緩，即影響因子變化率會保持在 0.4% 以內。由此可以確定，加筋板長寬比對影響因子的作用可以忽略不計，即加筋板長寬比對其極限承載力的影響可以忽略。

2.2 加筋板厚度與影響因子的關系

船用加筋板的厚度一般在 8 mm 左右，對于特殊的大型船舶和軍船，加筋板的厚度可能會超過 10 mm。因此，加筋板的厚度在 6 mm 到 14 mm 之間均勻取值進行計算，計算結果見表 3。為了保持變量為無量綱因子，將加筋板厚度t與加筋板寬度b的比值作為因變量。將計算結果繪制成圖，如圖 6 所示。

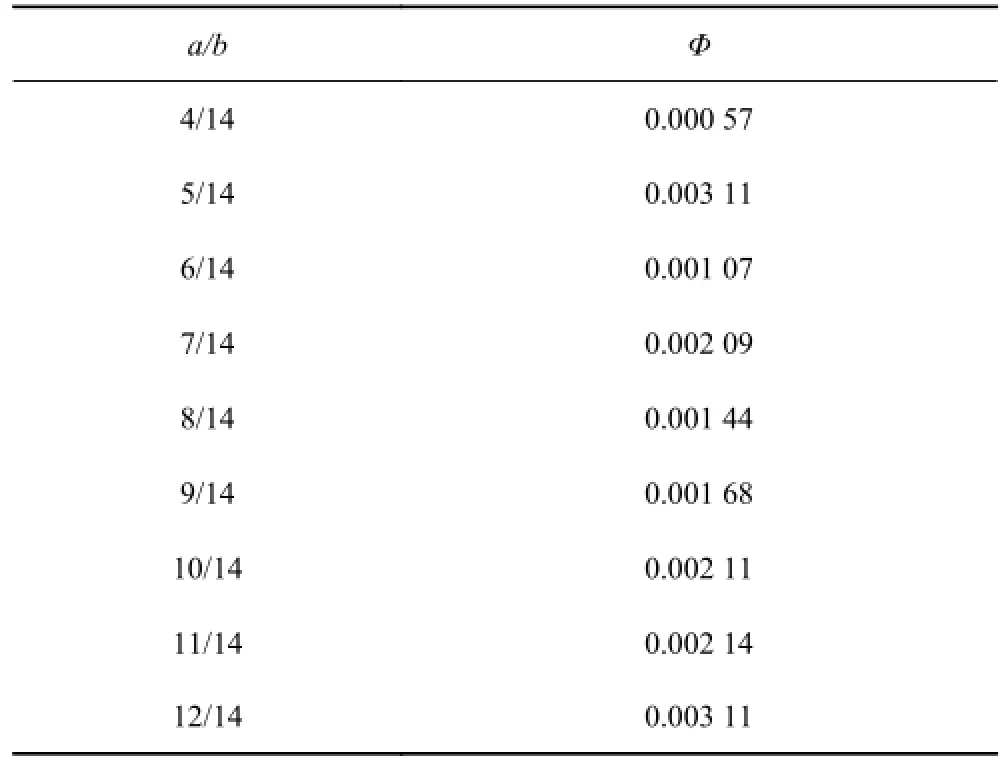
表2 φ 隨加筋板長寬比a/b的變化Tab. 2 φ varies witha/b

從圖 6 可以看出，隨著加筋板厚度t的增大，影響因子 φ 先減小然后增大，變化規律可以近似看成二次函數的關系。利用 Matlab 可以得到擬合的二次函數關系：

擬合函數數據與原始數據最大誤差為 0.1% 左右，符合工程要求。擬合函數符合實際情況。利用擬合函數可以確定影響因子最小點，設計過程中在最小點附近取值板厚，可以保證較小的影響因子。

2.3 加強筋間距與影響因子的關系

考慮加強筋間距對影響因子φ的影響，對加強筋間距的控制，主要是通過改變加強筋的數量來實現，即保持加筋板的寬度b保持不變。根據統計規律，船用加筋板上加強筋一般在 2 根以上。因此，加筋板數量取 2～9 進行計算，計算結果見表 4。為了保持變量為無量綱因子，將加強筋間距s與加筋板寬度b的比值作為因變量。將計算結果繪制成圖，如圖 7所示。

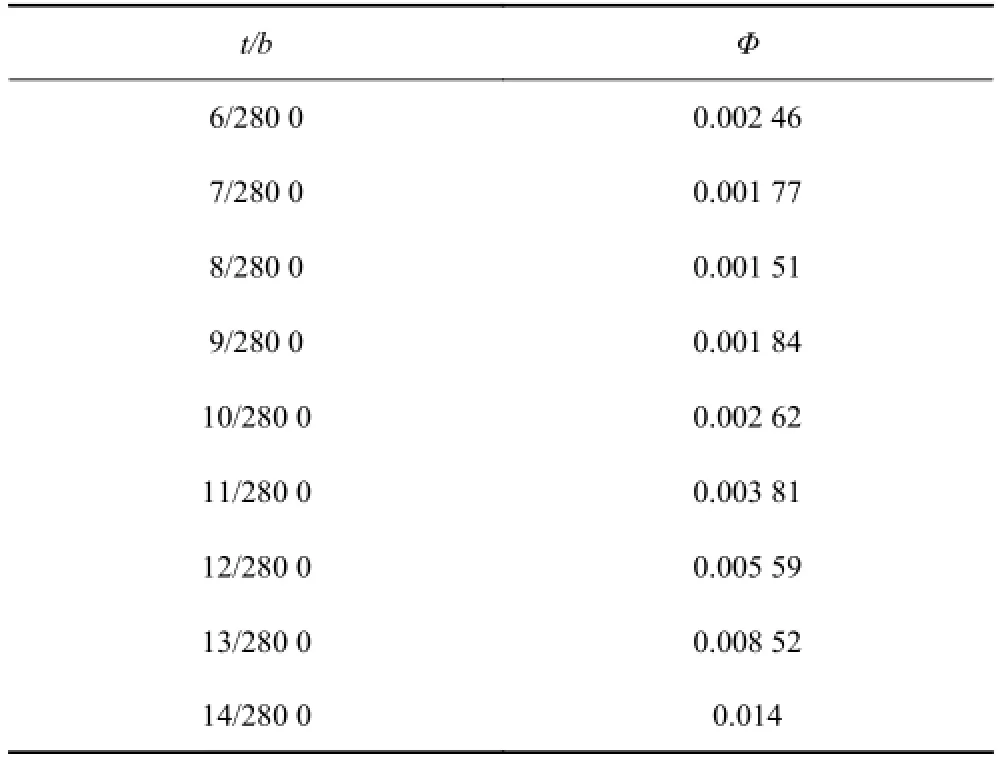
表3 φ 隨t/b的變化規律Tab. 3 φ varies witht/b

表4 φ 隨s/b的變化規律Tab. 4 φ varies withs/b

從計算數據可看出，隨著加強筋間距的增大，影響因子 φ 也逐漸減小，并出現負值，即加筋板的穩定性增強。根據圖 7 可得，當加強筋間距較小時，即s/b小于 1/7 時，影響因子的變化率較小。所以，對于密加筋板，加強筋間距對影響因子的影響作用可以忽略不計。當加強筋間距比較大時，初始撓度對加筋板的穩定性具有一定的增強作用。這就說明，當加筋板產生初始撓度之后，加強筋對穩定性的作用減弱，而在實際加筋板設計過程中，加強筋用于增強其穩定性，因此，可以綜合考慮初始撓度和加強筋對穩定性的作用進行設計。

3 結 語

1）初始撓度對加筋板的彈性失穩壓力影響較大，且隨著初始撓度的幅值和半波數的增加，彈性失穩壓力不斷變小。

2）對于含有某種初始撓度的加筋板，其影響因子主要受加筋板的厚度和加強筋間距的影響，加筋板的長寬比影響較小，可以忽略。

3）影響因子的確定方法，滿足工程要求，具有一定的可行性，可應用于船舶結構設計，完善結構設計規范。

[ 1 ]張濤, 劉土光, 趙耀, 等. 初始缺陷加筋板的屈曲與后屈曲分析[J]. 船舶力學, 2003, 7(1): 79-83.

[ 2 ]王偉, 吳梵. 國內船舶結構穩定性研究進展[J]. 船舶工程, 2010, (32): 5-9.

[ 3 ]EIRIK B. Semi-analytical model for global buckling and postbuckling analysis of stiffened panels 2004[J]. Thin-Walled Structures. 2004, (42): 701-717.

[ 4 ]王偉, 吳梵. 單根加筋板整體屈曲臨界應力計算與分析[J].艦船科學技術, 2010, 32(10): 3-7. WANG Wei, WU Fan. Calculating and analysis of the overall buckling’s critical stress of single stiffened panels[J]. Ship Science and Technology, 2010, 32(10): 3-7.

[ 5 ]單成巍. 循環載荷作用下船體結構的極限強度非線性有限元分析[D]. 武漢：武漢理工大學, 2013.

[ 6 ]楊淼. 基于 HCSR 的加筋板格非線性屈曲研究[D]. 大連：大連理工大學, 2011.

[ 7 ]萬育龍, 朱旭光. 加筋板屈曲和極限強度有限元計算方法研究[J]. 船海工程, 2013, 42(6): 17-21.

[ 8 ]TEIXEIRA A P, IVANOV L D, GUEDES SOARES C. Assessment of characteristic values of the ultimate strength of corroded steel plates with initial imperfections[J]. Engineering Structures, 2013, 56: 517-527.

[ 9 ]DONNELL L H. Effect of imperfection on buckling of thin cylinders under external pressure[J]. Journal of Applied Mechanics. Trans, ASME, 1956.

[10]張二. 初始幾何缺陷對錐-環-柱結合殼力學性能影響研究[D]. 武漢：海軍工程大學, 2015.

[11]張曉丹, 楊平. 加筋板在軸向壓力下的極限強度研究[J]. 武漢理工大學學報, 2011, 35(2): 305-308.

The buckling analysis of the stiffened plate with initial deflection

LIU Chun-zheng, WU Fan, MU Jin-lei
(Naval University of Engineering, Department of Naval Architecture, Wuhan 430033, China)

For the research, the mode of the initial deflection was regarded as the double trigonometric series based on the practical truth and the effect of the amplitude and the number of half-waves on the critical stress entirely was analyzed by computing with ANSYS. The impact factor of the initial deflection was obtained. Results indicate that with the increasing of amplitude and the number of half-waves, the critical stress decreases. For the stiffened plate with one kind of initial deflection, the impact factor is up to the thickness of the stiffened plate and the space between stiffeners. The length-width ratio has little influence on the impact factor and it can be ignored.

initial deflection；stiffened plate；stability；amplitude；the number of half-waves；impact factor

U663.6

A

1672 - 7619(2017)04 - 0040 - 05

10.3404/j.issn.1672 - 7619.2017.04.008

2016 - 06 - 24；

2016 - 07 - 07

國家自然科學基金資助項目(51309231)

劉春正(1991 - )，男，碩士研究生，研究方向為船舶結構強度與振動。