對數(shù)函數(shù)的FPGA實現(xiàn)

盧小冰

摘 要：CORDIC算法常用于高效地實現(xiàn)多種超越函數(shù)求值，但算法的通用性使其在FPGA上的實現(xiàn)具有一定的難度。利用此算法在對數(shù)方面的推導(dǎo)公式，介紹一種基于查表、移位、加法及除法等操作，在FPGA上得以實現(xiàn)的方法。

關(guān)鍵詞：坐標(biāo)旋轉(zhuǎn)數(shù)字計算機(jī)（CORDIC）算法 對數(shù)函數(shù) FPGA實現(xiàn) 查表法

中圖分類號：TP302 文獻(xiàn)標(biāo)識碼：A 文章編號：1672-3791（2017）03（c）-0204-02

對數(shù)函數(shù)在粒子濾波、RBF神經(jīng)網(wǎng)絡(luò)、圖像處理等領(lǐng)域廣泛運用。CORDIC算法（The Coordinate Rotation Digital Computer）是一種用于計算一些常用的基本運算函數(shù)和算術(shù)操作的循環(huán)迭代算法。CORDIC算法主要由加法、移位實現(xiàn)，從而大大降低了占用的FPGA資源。該文介紹一種由CORDIC算法推導(dǎo)的對數(shù)函數(shù)在FPGA上的實現(xiàn)。

1 CORDIC算法

1.1 CORDIC算法基本原理

CORDIC算法主要用于計算三角函數(shù)、雙曲函數(shù)、指數(shù)和對數(shù)，其基本思想是通過一系列固定的與運算基數(shù)相關(guān)的角度不斷偏擺來逼近所需的旋轉(zhuǎn)角度，使得矢量旋轉(zhuǎn)和定向運算不需要三角函數(shù)查表及乘、開方、反三角函數(shù)等復(fù)雜的數(shù)學(xué)運算，其原理如圖1所示。對于矢量旋轉(zhuǎn)角度變成，則有：

式中，。CORDIC算法一般工作在旋轉(zhuǎn)和矢量兩種模式下。旋轉(zhuǎn)模式為將矢量旋轉(zhuǎn)一個給定的角度；矢量模式為將輸入矢量旋轉(zhuǎn)到軸，同時記錄下旋轉(zhuǎn)的角度。文獻(xiàn)中給出了CORDIC算法具體的公式推導(dǎo)和兩種工作模式下次迭代后的最終結(jié)果。

1.2 CORDIC算法的對數(shù)運算推導(dǎo)

根據(jù)對數(shù)和反雙曲余切函數(shù)的線性關(guān)系，以10為底的對數(shù)可以通過計算反雙曲余切函數(shù)得到：

2 算法中的FPGA實現(xiàn)

2.1 算法的設(shè)計

CORDIC算法推導(dǎo)的對數(shù)函數(shù)，是基于小數(shù)跟的乘積，考慮到FPGA小數(shù)實現(xiàn)的問題，將其轉(zhuǎn)換為：

（3）

從式子可以看出，算法將由小數(shù)乘法轉(zhuǎn)換為移位加法求和后的乘法，從而大大降低硬件電路的復(fù)雜性。其次，的實現(xiàn)是通過查表法在FPGA中實現(xiàn)。

2.2 算法的實現(xiàn)

CORDIC算法的實現(xiàn)主要通過簡單的移位算法、高速流水線處理及查表查詢完成。簡單移位及高速流水線處理，快速精確完成式子（3）的系數(shù)的計算，同時對反正切函數(shù)的參數(shù)進(jìn)行處理，反正切函數(shù)參數(shù)涉及除法，采用ip核完成得到參數(shù)；取得參數(shù)后，通過查表法，對應(yīng)讀出存儲在ram中的反正切函數(shù)值，此步驟簡化了反正切函數(shù)高難度高復(fù)雜度的運算量，大大提高了運算速度及效率。最后，通過IP核完成乘法運算。整個算法過程，簡化了復(fù)雜的運算步驟，便于在FPGA上的實現(xiàn)。

2.3 算法的實現(xiàn)結(jié)果

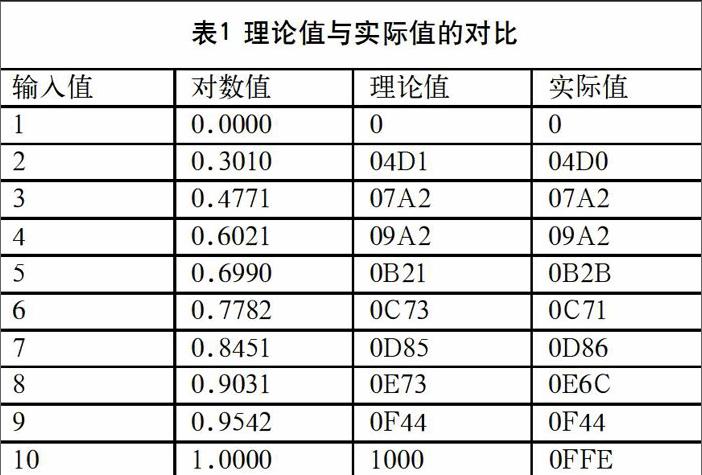
算法在Diamond 3.0軟件環(huán)境下，使用Verilog HDL語言實現(xiàn)以上算法，并在Lattice公司的ECP2M系列芯片LFE2M20 E7F256C中進(jìn)行驗證，采用Diamond提供的邏輯分析儀取得分析結(jié)果，分析結(jié)果如圖1所示，系統(tǒng)時鐘采用27 MHz；表1為理論值與實際值的對比；結(jié)果表明該設(shè)計達(dá)到要求。

3 結(jié)語

CORDIC算法推導(dǎo)出的對數(shù)函數(shù)在FPGA中的運用，已經(jīng)在Lattice芯片得到驗證，驗證結(jié)果與理論值一致。同時，若對模塊稍加修改同樣可以移植到其他的系統(tǒng)中，這對大多數(shù)對系統(tǒng)資源比較敏感的嵌入式系統(tǒng)來說更具有很強的現(xiàn)實意義。

參考文獻(xiàn)

[1] 閻嘯，秦開宇，高援開，吳紹煒. 基于CORDIC算法的頻譜分析技術(shù)研究[J].電子科技大學(xué)學(xué)報，2006，35（3）：335-338.

[2] Andraka Ray.A survey of CORDIC algorithms for FPGA base computer[C].In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays，1998：191-200.

[3] Muller J M.A few results on table-based methods[J].Reliable Computing，1999，5（3）：279-288.