汽車非線性懸架系統的穩定性分析

成 潔

（武警后勤學院，天津 300309）

汽車懸架系統是典型的非線性系統，非線性振系中可有不止一個平衡點（定點，奇點），其中有些可能是穩定的，另一些則可能是不穩定的。對于懸架系統，選取不同的系統參數會使系統具有不同的穩定性，因此有必要研究非線性懸架系統在周期外力擾動下的穩定性。

1 力學模型及運動微分方程

以研究垂直振動為目的建立汽車的動力學模型，本文采用1/4車體模型分析車輛特性。這里只考慮懸架彈簧的非線性剛度特性。變剛度彈簧的回復力-位移關系可表示為[1]：

式中：Fs為彈簧回復力，k為彈簧剛度，x為彈簧位移，ε為一表示彈簧非線性程度的小參數，ε=0時，該彈簧為線性。其力-位移關系曲線如圖1所示，虛線代表線性彈簧的回復力-位移曲線，實線代表非線性彈簧的回復力-位移曲線。

圖 2為懸架系統的力學模型。其中 m2為簧載質量，m1為非簧載質量，k1為輪胎剛度，c2為減振器粘性阻尼系數，z2為簧載質心垂直位移，z1為非簧載質心垂直位移，z0為路面不平激勵，F(z2- z1)為非線性彈性力。

圖1 變剛度彈簧力—位移曲線

圖2 兩自由度懸架振動模型

系統的運動微分方程為：

式中：——簧載質心的速度和加速度；——非簧載質心的速度和加速度。

選取下述狀態變量：

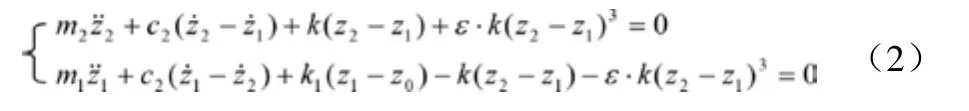
有下列方程：

選取車身加速度，車輪動位移，懸架動擾度三個性能指標作為輸出變量。

，乘以 k1后為車輪動載荷，x1= z2- z1為懸架動擾度。

2 懸架系統的穩定性分析

所謂解的穩定性[2]，是指系統在擾動下能夠自動返回原來的運動狀態的性能。根據線性穩定性定理：如果非線性方程的線性化方程的定點是漸進穩定的，則參考點（態）xi0是非線性方程的漸進穩定解；如果線性化方程的定點是不穩定的，則參考態是非線性方程的不穩定解。

當狀態變量的個數n>2時，系統在定態xi0鄰域的的線性化方程可寫成適量形式：

式中： 是n列（1×n）矢量，系數矩陣A取下面的形式：

方程（7）的基本解為：

代入方程（7），得：

齊次代數方程有非平凡解的條件是：

可寫為如下形式：

當方程（11）的所有特征值λi的實部Reλi都取負值時，解的每一項才收斂，這時定態才是漸進穩定的；反之，只要有一個特征值λi的實部取正值，定態就是不穩定的。

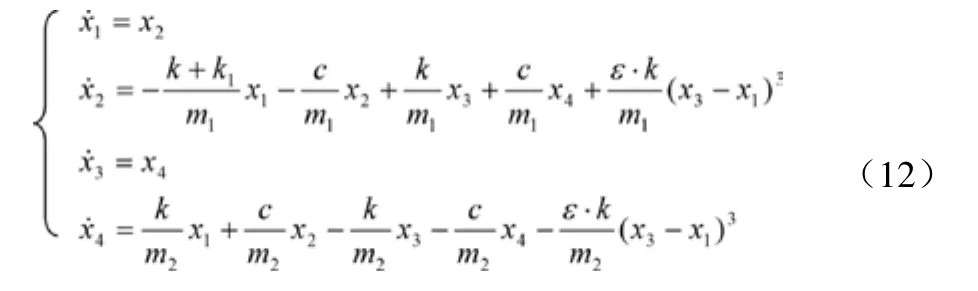
令，平衡點為(0,0,0,0)，(0,0,±3.162i,0)（舍去）。對于平衡點(0,0,0,0)

所以在平衡點(0,0,0,0)處的特征方程為：

根據羅斯—霍維茲判據[3]，△1＞0，△2=0，所以平衡點是穩定的，但不是漸進穩定的。

在系統沒有受到外界激勵時，車身相軌線和車輪相軌線如圖（3），（4）所示，分別由初始狀態呈螺旋狀回到平衡態。

圖3 相平面上的軌線

圖4 相平面上的軌線

當系統受到外界周期擾動激勵時，令F=Asin(wt)，ε=0.1（硬特性彈簧），懸架的結構參數為：m2=1091.49kg，m1=162.51kg，c=3235Ns/m，k=94835N/m，k1=1164593N/m。固定 A=0.5m，初始條件為x1=0，x2=0，讓w在本文研究的時間頻率范圍內（0.5-30Hz）變化。

當w分別為9rad/s、30rad/s、85rad/s時，車身和車輪相軌跡分別如圖5—10所示。可以看到，車身和車輪的相軌跡都分別從初始狀態經暫態后繞定點（原點）旋轉，成為一封閉的圓環。說明車身和車輪都在做穩定的周期震蕩。

圖5 相平面上的軌線

圖6 相平面上的軌線

圖7 相平面上的軌線

圖8 相平面上的軌線

圖9 相平面上的軌線

圖10 相平面上的軌線

3 結論

汽車懸架系統的穩定性在分析汽車振動特性中至關重要，它是關于懸架特性一切研究的基礎。本文結合實例分別對單自由度懸架系統和兩自由度系統的穩定性作出分析，可以看到：在本文所研究的時間頻率范圍內（0.5Hz—30Hz，它能夠覆蓋汽車系統的車身、座位和車輪的固有頻率范圍），具有弱非線性的懸架系統是穩定的。

參考文獻

[1] 張慧鵬.車輛非線性懸架系統動態特性[J].拖拉機與農用運輸車,2007,(04)58-62.

[2] 劉秉正,彭建華. 非線性動力學.高等教育出版社,2004.1.

[3] 諸德超,邢譽峰主編.工程振動基礎.北京航空航天大學出版社, 2014.