雷諾數(shù)對太陽能飛機氣動特性的影響研究

摘 要：太陽能飛機的相對速度較低，高空飛行可能面臨低雷諾數(shù)帶來的氣動問題。采用經(jīng)典的面元法二維程序，對典型的FX低速翼型進行了不同雷諾數(shù)的計算評估，分析了氣動力系數(shù)、轉(zhuǎn)捩點等隨雷諾數(shù)的變化特點。將二維拓展至三維情形，采用RANS求解器，對某太陽能飛機的幾個典型高度工況進行了全機氣動特性的計算分析，證實二維翼型的雷諾數(shù)影響規(guī)律對于三維全機仍然是適用的。當雷諾數(shù)顯著降低時，氣動特性通常也會有一定程度的惡化，在太陽能飛機的初步設(shè)計階段就應(yīng)該對雷諾數(shù)的影響進行充分的分析評估。

關(guān)鍵詞：太陽能飛機；雷諾數(shù)；CFD；氣動特性

前言

太陽能飛機[1]是一種依靠太陽能作為主要能源的飛行器，具有清潔、環(huán)保、低能耗、長航時等典型特征，是未來飛行器發(fā)展的方向之一。在太陽能無人機方面，誕生了“太陽神號”“西風號”等飛機，這些飛機雖然暫時在實用性方面仍存在缺陷，但在續(xù)航時間、飛行高度上均顯現(xiàn)出了巨大潛力；在載人太陽能飛機方面，“挑戰(zhàn)者號”“陽光動力號”等均進行了有益地嘗試，其中“陽光動力2號”在2016年完成了太陽能飛機的首次環(huán)球飛行。在國內(nèi)，由上海奧科賽飛機有限公司主導(dǎo)研發(fā)的“墨子號”太陽能飛機于2016年12月成功完成首飛，標志著國內(nèi)相關(guān)領(lǐng)域取得了重大突破。

不同時期的太陽能飛機都有一個顯著的共同點，即承載了當時在氣動、結(jié)構(gòu)、能源、材料等領(lǐng)域的高新技術(shù)。在太陽能飛機的設(shè)計過程中，涉及氣動布局優(yōu)化設(shè)計、大展弦比機翼結(jié)構(gòu)設(shè)計、飛行控制技術(shù)、輕質(zhì)高效的太陽能電池技術(shù)與儲能技術(shù)、能源管理系統(tǒng)、高效電推進系統(tǒng)、高空大氣環(huán)境研究等若干項關(guān)鍵技術(shù)[2]。

在氣動方面，由于大氣具有反射、散射及吸收等固有特點，隨著飛行高度的增加，太陽輻射的強度也越高，有利于太陽能飛機收集能量，而高度增加，帶來的問題是飛行雷諾數(shù)的減小，飛機的升阻特性也會發(fā)生一定的改變，因此，發(fā)展一款太陽能飛機，首先要解決的問題是要求氣動布局需要能適應(yīng)較為寬廣的高度范圍，摸清在不同雷諾數(shù)的氣動規(guī)律。本文基于CFD方法，針對典型的低速翼型研究了高低空環(huán)境下不同雷諾數(shù)的氣動特性，分析了升阻力、轉(zhuǎn)捩點等隨雷諾數(shù)變化的規(guī)律。并將分析模型從二維拓展至三維，對全機進行了數(shù)值仿真，證實這些規(guī)律對于三維情形仍然是適用的。

1 雷諾數(shù)對翼型氣動特性的影響

1.1 計算方法及算例驗證

XFOIL是一款經(jīng)典的面元法軟件，可進行無粘及有粘計算，并且加入了en轉(zhuǎn)捩預(yù)測方法，實現(xiàn)固定轉(zhuǎn)捩或自由轉(zhuǎn)捩計算，具有非常高的計算效率。

XFOIL采用簡單的線性渦分布面元法進行無粘計算。在速度較高時，采用卡門-錢壓縮性修正，使得XFOIL理論上可以計算整個亞音速范圍內(nèi)的任意速度，修正公式：

在獲得翼型壁面的壓力分布后，通過積分，可獲得翼型的升阻力系數(shù)及俯仰力矩系數(shù)。

為了檢驗XFOIL計算的準確度，采用LS0417翼型進行算例驗證。該翼型是由NASA發(fā)展的高升力翼型，具有比較大的升力系數(shù)。公開文獻給出了豐富的風洞試驗數(shù)據(jù)[3]，可用于考核計算軟件的可信度。

計算條件與試驗一致，馬赫數(shù)為0.15，雷諾數(shù)為4×106，迎角范圍-5-20.5°。計算結(jié)果與試驗結(jié)果的相關(guān)曲線如圖1所示，由圖可知，對于升力，在線性段計算與試驗吻合得非常好，隨著迎角增加，非線性現(xiàn)象變得顯著，計算誤差也逐漸增大。誤差對比詳見表1，最大誤差小于12%，顯然，這對于工程設(shè)計的早期階段是可接受的。通過計算驗證，證實XFOIL的可信度，可用于后續(xù)的太陽能飛機翼型氣動特性分析。

1.2 翼型氣動特性隨雷諾數(shù)的變化規(guī)律

從某種角度來說，翼型在一定程度上決定了飛機氣動特性的優(yōu)劣，因此，翼型的選擇及設(shè)計占據(jù)有非常重要的地位。針對太陽能飛機的翼型，提出如下要求：

（1）高升力要求。太陽能飛機通常屬于低速飛機，在升力系數(shù)足夠的情況下，可以不再設(shè)計襟翼等增升裝置，這樣可以獲得最小的重量代價，提高留空時間，但這樣對翼型的最大升力系數(shù)提出了較高的要求。

（2）低阻要求。飛行期間，所能獲得的太陽能能量及儲存的能量相對而言是比較有限的，要求飛機平臺具有良好的低阻特征，保證巡航及爬升時具有較高的升阻比。

（3）力矩方面，低頭力矩不能太強，以避免過大的配平損失。

基于上述要求，綜合對各類型各系列的翼型進行評判，可以選擇出適用于太陽能飛機的翼型。本節(jié)以FX 63-120翼型為例，研究雷諾數(shù)的影響。

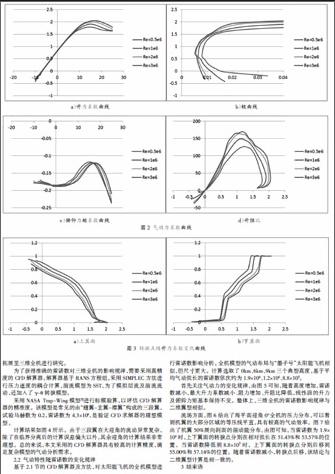
計算雷諾數(shù)覆蓋了從低空到高空的典型范圍，即0.5×106-3×106。計算結(jié)果如圖2所示。由圖可知，隨著雷諾數(shù)降低，最大升力系數(shù)減小，失速迎角提前，阻力系數(shù)增加，力矩特性基本維持不變，總的來說，雷諾數(shù)降低后，氣動性能會有所惡化。

圖3進一步給出了轉(zhuǎn)捩位置隨升力系數(shù)的變化曲線，隨著雷諾數(shù)降低，轉(zhuǎn)捩點后移，該結(jié)論與文獻[4]的翼型試驗基本一致。而層流本身抵抗分離的能力弱于湍流，這也是誘使分離提前、失速迎角減小的因素之一。

2 雷諾數(shù)對三維全機的影響

2.1 數(shù)值方法及標模驗證

通過對不同雷諾數(shù)的翼型氣動特性的研究，大致掌握了一般性規(guī)律，但二維翼型與三維全機仍存在很大差異，二維計算中無法評估機翼的誘導(dǎo)阻力、翼根與翼梢的三維效應(yīng)、以及機翼對平尾下洗的影響等，因此有必要在雷諾數(shù)對翼型影響評估的基礎(chǔ)上，進一步拓展至三維全機進行研究。

為了獲得準確的雷諾數(shù)對三維全機的影響規(guī)律，需要采用高精度的CFD解算器。解算器基于RANS方程組，采用SIMPLEC方法進行壓力速度的耦合計算，湍流模型為SST，為了模擬層流及湍流流動，還加入了γ-θ轉(zhuǎn)捩模型。

采用NASA Trap-Wing模型[5]進行標模驗算，以評估CFD解算器的精準度。該模型是常見的由“縫翼-主翼-襟翼”構(gòu)成的三段翼，試驗馬赫數(shù)為0.2，雷諾數(shù)為4.3×106，是驗證CFD求解器的理想模型。

計算結(jié)果如圖4所示。由于三段翼在大迎角的流動異常復(fù)雜，除了在臨界分離后的計算誤差偏大以外，其余迎角的計算結(jié)果非常理想。總的來說，本文采用的CFD解算器具有較高的計算精度，滿足復(fù)雜模型的氣動分析需求。

2.2 氣動特性隨雷諾數(shù)的變化規(guī)律

基于2.1節(jié)的CFD解算器及方法，對太陽能飛機的全機模型進行雷諾數(shù)影響分析。全機模型的氣動布局與“墨子號”太陽能飛機相似，但尺寸更大。計算選取了0km、6km、9km三個典型高度，基于平均氣動弦長的雷諾數(shù)依次約為1.9×106、1.2×106、8.8×105。

首先關(guān)注氣動力的變化規(guī)律，由圖5可知，隨著高度增加，雷諾數(shù)減小，最大升力系數(shù)減小、阻力增加、升阻比降低，線性段的升力及俯仰力矩基本保持不變。整體上，三維全機的雷諾數(shù)影響規(guī)律與二維翼型相似。

流場方面，圖6給出了海平面迎角0°全機的壓力分布，可以看到機翼的大部分區(qū)域的等壓線平直，具有較高的氣動效率。圖7給出了機翼50%展向剖面的湍動能分布，由圖可知，當雷諾數(shù)為1.9×106時，上下翼面的轉(zhuǎn)捩點分別在相對弦長在51.43%和53.57%的位置，當雷諾數(shù)降低到8.8×105時，上下翼面的轉(zhuǎn)捩點分別后移到55.00%和57.14%的位置。隨著雷諾數(shù)減小，轉(zhuǎn)捩點后移，該結(jié)論與二維翼型計算是相一致的。

3 結(jié)束語

針對太陽能飛機的飛行高度包線寬廣引起的雷諾數(shù)對氣動特性的影響問題，采用數(shù)值計算方法對二維翼型和三維全機進行研究，得到的結(jié)論如下：

（1）氣動力方面，二維翼型和三維全機受雷諾數(shù)影響的規(guī)律基本相似。隨著飛行雷諾數(shù)減小，最大升力系數(shù)、失速迎角均減小，阻力系數(shù)增加，線性段的升力系數(shù)及俯仰力矩系數(shù)變化不大，總體上氣動力呈惡化趨勢。

（2）流場方面，雷諾數(shù)降低后，轉(zhuǎn)捩點后移。

（3）通常太陽能飛機的飛行高度較高，雷諾數(shù)變化范圍較大，建議在設(shè)計階段對雷諾數(shù)影響予以足夠的關(guān)注，全面評估并充分掌握高空及低空的氣動特性。

參考文獻

[1]趙長輝，陳立瑋，等.太陽能電動飛機技術(shù)發(fā)展綜述[A].第五屆中國航空學會青年技術(shù)論壇[C].2012.

[2]高廣林，李占科，等.太陽能無人機關(guān)鍵技術(shù)分析[J].飛行力學，2010，28（1）：1-4.

[3]Robert J. McGhee，William D. Beasley， Richard T. Whitcomb.ASA Low-and Medium-speed Airfoil Development[J].ASA-TM-78709，1979.

[4]卞于中，何可敏，等.湍流度和雷諾數(shù)對附面層轉(zhuǎn)捩位置的影響[J].流體力學實驗與測量，1997，11（1）：25-29.

[5]李萍，李根國，等.NASA高升力TrapWing全展模型的數(shù)值模擬[J].力學季刊，2012，33（2）：249-255.

作者簡介：毛一青（1965-），男，上海奧科賽飛機有限公司總設(shè)計師，從事飛機總體設(shè)計方面的研究。