頂點P_k覆蓋問題的研究綜述

王利民 華景煜

摘要頂點覆蓋問題是經典的NP完全問題，在排序、計算機網絡等現實生活中有許多的應用.近幾年來，許多研究者開始探究它的推廣形式——頂點P_k覆蓋（VCPP_k）問題，即尋找一個頂點子集，從拓撲結構圖中刪除后使得剩下的頂點導出的子圖不包含P_k路，其中P_k是指包含k個頂點的路.本文簡單介紹了VCPP_k問題的應用背景，歸納了它在近似算法、精確算法、參數化算法3個方面的主要研究進展，并分析了一些主要的方法和技巧.在此基礎上，對VCPP_k問題及其相關問題的研究前景進行了展望.關鍵詞頂點P_k覆蓋；近似算法；精確算法；參數化算法

中圖分類號TP391.7

文獻標志碼A

0 引言

頂點覆蓋問題是一個經典的NP完全問題，它與團問題、獨立集問題等可以互相轉換，在排序、計算機網絡等現實生活中有許多的應用.近幾年來，許多研究者開始探究它的推廣形式——頂點P_k覆蓋（VCPk，k≥3）問題.這個問題是頂點刪除問題的一個特殊類型.頂點刪除問題就是尋找一個頂點子集，從拓撲圖中刪除這些頂點后，使得剩下的頂點導出的子圖滿足一個給定的特征.例如頂點P_k覆蓋問題，即尋找一個頂點子集，從拓撲結構圖中刪除這個子集后使得拓撲圖中剩下的頂點導出的子圖不包含Pk路，其中Pk是指包含k個頂點的路.

無線傳感器網絡是當前信息領域中研究的熱點之一，可用于特殊環境的信號采集、處理和發送.無線傳感器網絡是一種全新的信息獲取和處理技術，作為一種無處不在的感知技術，無線傳感器網絡廣泛應用于軍事、環境、醫療、家庭和其他商用及工業領域.在空間探索和反恐、救災等特殊的領域，傳感器技術和節點間的無線通信能力為無線傳感器網絡賦予了廣闊的應用前景.

在無線傳感器網絡越來越廣泛的現實生活應用中，人們主要關注的安全特性包括機密性、可靠性和數據的完整性等.由于傳感器自身的計算能力、電源儲備和處理信息的能力都有限，而且，它們通常部署在易受影響的區域，很容易被攻擊者攻擊或信息被竊取.傳統的安全協議不能直接應用到無線傳感器網絡中，因此，就安全研究領域來說，如何設計無線傳感器網絡的安全協議成為一個很大的挑戰.

許多學者在這方面進行了大量探究，例如，在傳感器網絡中，為了確保數據的完整性或數據來源認證，文獻[1]就設計了一個安全協議.為了確保數據的完整性，推廣的Canvas協議[2]提出在傳感器形成的通信圖中，對于每條長度為k-1的路徑中至少要有一個頂點沒有被捕獲.因此，在傳感器網絡的部署和初始化期間，應確保至少有一個受保護的頂點存在于每個長度為k-1的路徑中.又由于傳感器之間需要傳遞信息，以及對傳感器加以保護是需要費用的，為此在現實應用時還需要考慮傳感器節點之間的連通性，以及合理設計安全協議盡量減少費用.更多的實際應用可以參考文獻[3].

一般圖上的權值最小VCPP_k問題和所含頂點數最少的VCPP_k問題都是NP完全問題.本文重點介紹VCPP_k問題的研究成果包括：無向圖、有向圖和特殊圖的VCPP_k問題和參數化VCPP_k問題的相關算法，同時根據已有成果介紹一些可以值得研究的方向.下面給出VCPP_k問題的一些相關定義.

圖G=（V，E）是一個含有n個頂點的圖，V是G的頂點集，E是邊集.

定義1（含頂點數最少的VCPP_k，簡記MVCPk） 給定一個含有n個頂點的圖G，求一個含頂點數最少的VCPP_k.

定義2（權值最小的VCPP_k，簡記MWVCPP_k） 給定一個頂點帶權的圖G，求一個權值最小的VCPP_k.

一般圖上的MVCPP_k和MWVCPP_k問題的前期研究主要集中在一些性質、近似算法和精確算法，其中也包括頂點連通性，即使得求得的VCPP_k集導出的子圖是連通的.近幾年，許多學者開始關注VCPP_k問題的參數化，參數化VCPP_k問題的定義如下：

定義3（參數化不帶權的VCPP_k，簡記PVCPk） 給定含有n個頂點的圖G和一個非負整數k，能否在圖中找到一個含頂點個數不超過k的VCPP_k.

如果一個參數化NP難問題在時間f（k）nO（1）內可解，其中f（k）是僅關于k的一個函數，那么稱此問題是固定參數可解的（FixedParameter Tractable，簡記FPT）[4].

本文第1節介紹無向圖中VCPP_k問題的研究現狀；第2節主要描述無向圖中PVCPP_k問題的研究現狀；第3節給出一些特殊圖中VCPP_k問題的研究現狀；第4節介紹有向圖中VCPP_k問題的研究現狀；最后通過分析和總結，給出VCPP_k問題研究中可以考慮的幾個方面.

1 無向圖中的VCPP_k問題

本節主要介紹無向圖中VCPP_k問題的研究現狀，主要包括近似算法、精確算法和MVCPP_k的上下界.

1.1 近似算法

由于VCPP_k問題是NP完全問題，除非P=NP，否則VCPP_k問題不可能有多項式時間算法，因此前期學者對最小VCPP_k問題的研究主要集中在多項式時間可解的近似算法.近似算法主要是在最壞的情況下找到問題的近似解與最優解的比值；即算法的近似度.近似算法主要的衡量指標之一就是近似度.下面主要分析MVCPP_k和MWVCPP_k問題的近似算法.對于MWVCPP_k問題，算法的近似度為近似解與最優解的權值的比值，對于MVCPP_k問題，近似度為近似解與最優解所含頂點數目的比值.

文獻[5]利用以某概率選擇頂點的方法得到MVCP3問題的一個近似比期望為2311的隨機算法.Tu等[67]利用原始對偶算法或分層技巧分別給出權值最小的VCP3問題的一個2因子近似解.文獻[6]通過在原圖上添加懸掛邊的方法，將權值最小的頂點覆蓋問題歸約到權值最小的VCP3問題，證明VCP3問題是NP難解的.

文獻[8]首先利用逐步刪除P_k的貪婪算法和添加頂點的方法給出了最小的連通VCPk問題的一個k2近似解，進而結合平面的劃分和轉移策略給出這個問題在單位圓盤圖上的一個多項式時間近似格式的算法.這個算法的整體設計思路如下：首先，定義一個正方形區域使得這個區域包含圖中的所有單位圓盤，再將這個區域劃分成一些小的正方形.對每一個小正方形，定義它的中心區域和邊界區域.其次，對于單位圓盤圖，采用一個常因子的近似算法求得圖的一個連通的VCPk集，使得這個近似解中每個頂點的權值至多是c，這里c是一個正的常數.然后，對于每個正方形的中心區域，枚舉所有的VCPP_k集，僅僅考慮滿足鄰域條件的解，進而選擇頂點權和最小的一個解，將此解記作局部最優解.通過對邊界區域的選擇，可以確保算法的輸出結果是一個連通的VCPP_k集.最后將常因子近似解落在某個劃分的邊界區域的頂點集合與局部最優解合并.一般地，將正方形區域的左下角沿著45°角移位，每次移動2個單位就得到一個新的劃分.其中采用轉移策略是為了選取一個劃分使得常因子近似解落在這個劃分的邊界區域的頂點集合的權和或頂點個數盡可能小，從而使得輸出結果與最優解的比更小.而劃分策略或分治法主要是將一個難以直接解決的大問題，分割成一些規模較小的相同問題，各個擊破，分而治之，然后再利用這些子問題的解求出原問題的解.簡言之，縮小問題規模，使子問題易求解.在假設圖的圍長至少是k的條件下，Li等[9]利用深度優先搜索法及逐步加點判斷的方法提高了最小的連通VCPk問題在一般圖上的近似比，即給出一個k近似解，其算法時間復雜度為O（n2）.

文獻[10]提出最小連通有界VCPP_k的概念，并在假設圖的度有界的條件下，利用增長劃分的方法得到連通的VCPP_k問題在growthbounded圖上的一個多項式時間近似格式的算法，但是此時不需要利用常因子近似解.文獻[10]的主要思想是將圖劃分成一些聚類，然后對每一個聚類求局部解，進而合并這些解得到最后結果.

在假設圖的最小度為2的情況下，Wang等[11]首先利用原始對偶算法和有關頂點加權的斯坦納樹的一個近似算法得到權值最小的連通VCP3問題的一個常因子近似解；其次利用文獻[12]給出的最小連通頂點覆蓋問題在單位圓盤圖上的多項式時間近似格式算法的思想，結合一個類似c局部問題[13]的概念（c是一個正的常數），再利用平面上的劃分和轉移策略，給出權值最小的連通VCP3問題在單位圓盤圖上的一個多項式時間近似格式的算法.

在現實世界中，為了觀察某些復雜的環境，例如高山上或水里[14]，一些傳感器就被放在不同的深度，這就形成了三維空間的網絡，它可以模擬的數學模型是單位球圖.根據平面上研究的一些結論和受到的啟發，Wang等[15]提出一個弱c局部問題的概念（c是一個正的常數），并在頂點權值的光滑性條件下，利用高維空間的劃分和轉移技巧，給出權和最小的連通VCP3問題在單位球圖上的一個多項式時間近似格式的算法.當球的半徑不同時，上面的方法將不起作用.然而文獻[16]在球的最大半徑與最小半徑的比值有界的條件下，利用局部搜索的方法給出最小的VCPP_k問題在球圖上的一個多項式時間近似格式的算法.

注意到在處理連通的VCPP_k問題時，主要包含常因子的近似解、多項式時間近似格式的算法和特殊拓撲結構圖上的時間復雜度等3個方面.

對于求解常因子的近似解，一般地，先通過一些算法或技巧找到一個不連通的近似解，再結合求解斯坦納樹的算法或逐步添加頂點并判斷的方法，進而得到連通的常因子近似解.或者，先利用深度優先搜索法或其他搜索法得到拓撲結構的支撐樹，再對樹的每一分支判斷是否需要繼續添加頂點，從而得到所求的結果.因此，以后在求解連通的常因子近似解時就可以參考這2種方法.而設計多項式時間近似格式的算法，主要采取劃分策略和轉移策略，以及增長劃分策略2種方式，當圖中頂點的位置信息已知時大部分采取劃分和轉移策略，這是處理這類問題常用的技巧和方法.然而在更一般的圖上，如growthbounded圖上，不需要利用常因子近似解，只知道圖的部分信息，此時多采取增長劃分.不管是那種劃分策略，為了達到連通都需要使劃分的小區域有重疊的部分，算法最關鍵的地方就是處理重疊部分.

1.2 精確算法

近似算法只能得到問題的近似解而無法得到精確解，甚至許多問題很難求得近似解.于是許多學者開展了對VCPP_k精確算法的研究.顯然，通過枚舉圖中n個頂點的2n個子集就可以找到最小的VCPP_k.

對于VCP3問題，文獻[5]利用分支定界法逐步減少圖的頂點個數，從而求得MVCP3，其算法時間復雜度為O（1.517 1n），其中n是圖G的頂點個數.Chang等[17]利用加權分治技術提出一個分支化簡的算法，算法提高了上面的時間復雜度，其復雜度為O（1.465 8n）.文獻[18]根據給出的一些有關分散集和VCP3結構特征，利用更多的化簡規則和分支規則，提出了時間復雜度為O（1.465 6n）的精確算法，此時需要多項式空間；進一步利用動態規劃技術改進算法，其時間復雜度為O（1.365 9n），但是需要指數空間.

1.3 MVCPP_k的上下界

2 無向圖中的PVCPP_k問題

在實際應用中，圖的結構是比較復雜的且圖的頂點數n往往比較大，VCPP_k問題的所有精確算法都無法應用于實際.但是在很多實際應用中，VCPk的大小k比n小很多，而且有些應用不一定要找最小的VCPP_k，而只要求小于某個值的VCPP_k，于是許多研究者考慮研究VCPP_k問題的參數化.下面開始介紹無向圖參數化VCPP_k問題的研究現狀.

文獻[4]采用迭代壓縮技術證明一般圖上的PVCP3問題是固定參數可解的，即對于固定的參數k，這個問題可以在時間O（2kk3.376+n4m）內得到它的解，其中n是圖的頂點個數，m是圖的邊數，VCP3問題解的頂點個數至多是k.文獻[24]利用化簡規則和分支搜索技術給出PVCP3問題的一個FPT算法，其時間復雜度為O（1.817 2knO（1））.Chang等[25]也利用化簡規則和分支搜索技術在多項式空間和指數空間中分別說明PVCP3問題是固定參數可解的，算法所執行完成的時間至多分別為O*（1.796 4k），O*（1.748 5k），這里O*的含義為：對于2個函數f和g，如果f（k，n）=O（g（k）·poly（n）），那么f（k，n）=O*（g（k）），其中poly（n）是n的多項式函數.對于VCP4問題，Tu等[26]也利用迭代壓縮技術證明一般圖上的PVCP4問題是固定參數可解的，時間復雜度為O（3kn4）.

VCPP_k問題核心化是參數化VCPP_k問題的重要研究內容.如果在求解VCPP_k問題之前，利用核心化算法對問題規模進行簡化，將大大提高求解PVCPP_k的效率.對于VCP3問題，文獻[27]得到一個大小為15k的核，文獻[28]利用2次簡化規則提高這個核到6k-6，Brause等[29]利用皇冠分解給出一個計算核的多項式時間的算法，通過算法得到圖的2個不交的集合T1，T2，滿足|T2|≤6·ψ3（G[T2]），其中T2為圖G的核，可以看出此處核的上界為6k.最近，通過改進化簡規則，文獻[30]將該問題的核大小提高到5k.

3 特殊圖中的VCPP_k問題

對于特殊圖上的VCPP_k問題，許多學者也進行了大量的研究.某些特殊的應用對應一些在具有特殊性質的圖上的VCPP_k問題，而特殊圖上的VCPP_k問題比一般圖上的VCPP_k問題更容易，使得在特定條件下解決VCPP_k問題顯得更有意義.本節簡要闡述各類特殊圖中VCPP_k問題的研究現狀.

1） 三正則圖上的VCPP_k問題

三正則圖是指圖中所有頂點的度均為3的圖，也稱為立方圖.在三正則圖中，文獻[31]給出了一些有關VCP3問題的結論：首先，利用歸約證明在圍長為3的三正則平面圖中，最小VCP3問題的判定問題是NP完全的；其次，令ψ3（G）表示圖G的最小VCP3集的頂點數，得出2n5≤ψ3（G）≤n2；最后，利用逐步刪除頂點度為3的頂點的貪婪算法，給出最小VCP3問題的一個近似度為1.57的近似算法.在三正則圖中，文獻[32]給出了一些有關VCP4問題的結論：首先，利用歸約證明最小VCP4問題的判定問題是NP完全的；其次，令ψ4（G）表示圖G的最小VCP4集的頂點數，得出n4≤ψ4（G）≤n2；最后，利用Lovasz分解，給出最小VCP4問題的一個近似度為2的近似算法.

2） 完全圖、路、圈、樹上的VCPP_k問題

文獻[33]從時間復雜度的角度考慮，在完全圖、路和圈上分別可以在O（n·k）、O（n·k）和O（n·k2）時間內求出權值最小的VCPk問題的最優解，而在樹上的時間和空間復雜度均為O（n·k）.文獻[9]采取逐步判斷樹的分支是否含有Pk的方法，得到在樹上可以在O（n2）時間內求出最小連通的VCPk問題的最優解.文獻[34]通過尋找最長路以及逐步加點判斷的方法可以在O（n）時間內找到權和最小的連通VCPk問題的最優解；進一步得到在包含唯一圈（圈的長度為r）的圖上可以在O（nr）時間內找到這個問題的最優解.

3） 樹寬有界的圖的VCPP_k問題

在樹寬有界的圖中，文獻[35]設計了一個動態規劃算法可以求得MVCP3，其時間復雜度為4p·nO（1），其中樹寬至多是p.文獻[36]不僅提高了求MVCP3問題的時間復雜度3p·nO（1），而且針對連通的VCP3問題給出一個時間復雜度為4p·nO（1）的隨機算法.

4 有向圖中的VCPP_k問題

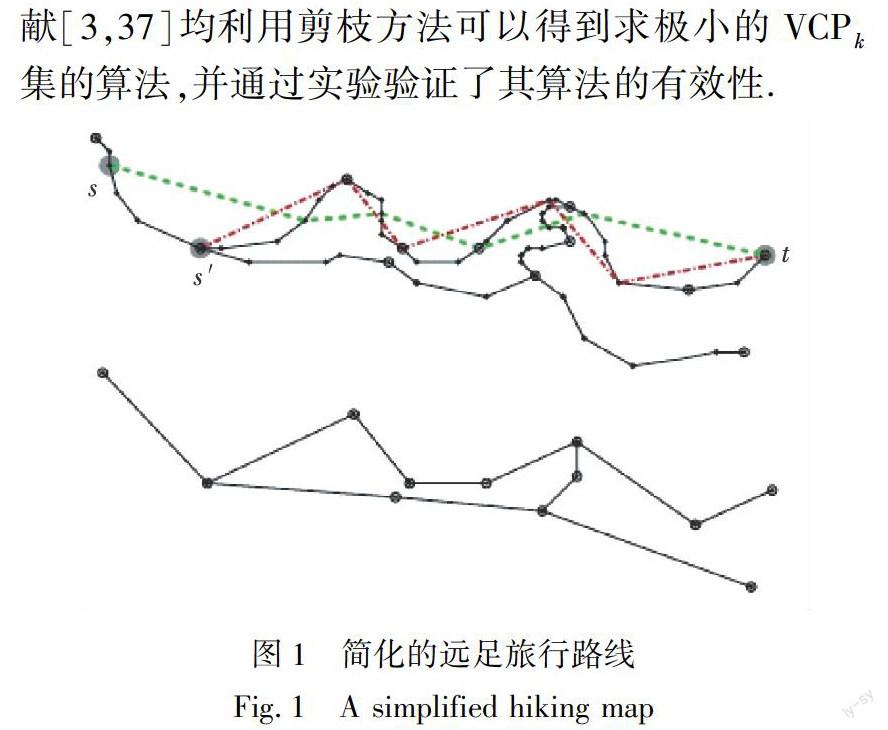
眾多研究者探究VCPP_k的相關問題主要集中在無向的拓撲結構圖上，對有向圖的VCPP_k問題的研究進展較為緩慢，主要是考慮方向后難度會更大.然而，近年來，文獻[3，37]分別從現實的生活環境和需求出發介紹了VCPP_k問題在有向圖環境中的一些應用實例（圖1）.例如：人們在遠足旅行時會通過一些網站查詢一下路線圖，網站會發送幾條建議遠足路線，路線中的每個節點都標記的話會浪費很多帶寬，因此，可以考慮只發送幾個關鍵的節點信息，刪除重疊的部分，使得路線圖顯得更清晰，便于出行者選擇合適的路線.如圖1，有2條出行路線紅色s′→t和綠色s→t可供選擇，只需選用灰圓圈標記的節點即可覆蓋整個圖（k=6時的情形）.在超大規模的圖中，文獻[3，37]均利用剪枝方法可以得到求極小的VCPP_k集的算法，并通過實驗驗證了其算法的有效性.

5 總結與展望

頂點覆蓋問題是一類重要的NP完全問題，在排序、計算機網絡等現實生活中有許多的應用.近幾年來，人們開始關注它的推廣形式——VCPk （k≥3）問題.本文著重闡述無向圖中VCPP_k問題的研究現狀.從中可以看出，前期較多的研究關注點是VCPP_k問題的性質和近似算法，而隨著參數計算理論的產生，推動了VCPP_k問題的發展，使之成為目前階段的研究熱點.

通過對VCPP_k問題研究現狀的總結和分析，可以使學者對VCPP_k問題有更全面的理解.當然對于VCPP_k問題，依然還有許多方面有待于我們進一步探究，主要可以從以下幾個角度進行研究.

1）VCPP_k問題的算法研究

在一般圖上對于權和最小的連通VCPP_k問題尚未有常因子近似解，是否可以根據已有結果及問題的自身特征尋求新穎的算法去求解，進而給出相應問題的一個多項式時間近似格式算法呢？ 處理這個問題的難點是如何使其連通.

對于權和最小的連通VCP3問題，所求的近似解是在最小度為2的情況下得到的，那么是否可以通過尋求新算法將圖的最小度降為1？求解這個問題的多項式時間近似格式的算法時，有假設條件c局部或弱c局部以及頂點權值是光滑性的等，考慮到現實環境，不太實用，能否采用其他的方法將c局部等條件去掉？

2）VCPP_k問題的核心化

許多學者對無向圖上VCPP_k問題的核心化研究已取得了一些結果，通過一系列局部簡化規則和對圖結構的分析，對核大小不斷進行改進.希望能夠通過深入分析已有結論和VCPP_k問題的結構，構造出更多的簡化規則，從而提出更好的核心化算法.

3）VCPP_k問題的變形

近年來，一部分研究者探究VCPP_k問題的一個變體——k連通子圖覆蓋問題，即尋找一個頂點子集，從圖中刪除后使得圖中剩下的頂點導出的子圖不包含k個頂點導出的連通子圖.可以看出這個問題比VCPP_k問題更具有一般性.在這方面的主要結論有：在假設圖是連通的條件下，文獻[9]利用深度優先搜索法、生成樹及逐步加點判斷的方法給出頂點連通的k連通子圖覆蓋問題的一個k近似算法.利用線性規劃舍入方法很容易得到權和最小的k連通子圖覆蓋問題的一個k近似解.然而在假設圖的圍長至少是k的情況下，文獻[38]提高了這個問題的近似比，首先利用圖的拓撲結構，并結合頂點的度權函數給出一個近似比，其次，利用類似分層的方法又得到一個近似比，兩者均為k-1.除了這2種情況有以上結果外，頂點不連通、不加權和頂點連通以及加權等情況尚未有人探討，而且就現階段的研究現狀來看，對于有關k連通子圖覆蓋問題的多項式時間近似格式算法還沒有研究者去探索，這可能也是一個比較好的研究方向.

4）VCPP_k問題的隨機算法

隨機化是現代計算機科學最重要的方法之一，近幾十年來被廣泛地應用于計算機科學的各個領域.在這些應用的背后，是一些共通的隨機化原理.我們是否可以利用一些重要的隨機算法的設計思想和理論分析，借助一些概率論工具及其在算法分析中的應用，從新的角度探索VCPP_k問題或k連通子圖覆蓋問題呢？

5） 特殊圖上的VCPP_k問題

根據一些特定的應用，對于特殊圖上VCPP_k問題的研究也很有意義.本文列舉了一些特殊圖上的VCPP_k問題，可以對這些問題的算法做進一步的研究，提出更有效的算法，或者對由實際應用而轉化的特殊VCPP_k問題進行研究.

參考文獻

References

[1] Menezes A J，Van Oorschot P C，Vanstone S A.Handbook of applied cryptography[M].Boca Raton：CRC Press，1996

[2] Novotny M.Design and analysis of a generalized canvas protocol[C]∥IFIP International Workshop on Information Security Theory and Practices，2010：106121

[3] Funke S，Nusser A，Storandt S.On kpath covers and their applications[J].The VLDB Journal，2014，25（1）：103123

[4] Tu J H.A fixedparameter algorithm for the vertex cover P3 problem[J].Information Processing Letters，2015，115（2）：9699

[5] Kardos F，Katrenic J，Schiermeyer I.On computing the minimum 3path vertex cover and dissociation number of graphs[J].Theoretical Computer Science，2011，412（50）：70097017

[6] Tu J H，Zhou W L.A primaldual approximation algorithm for the vertex cover P3 problem[J].Theoretical Computer Science，2011，412（50）：70447048

[7] Tu J H，Zhou W L.A factor 2 approximation algorithm for the vertex cover P3 problem[J].Information Processing Letters，2011，111（14）：683686

[8] Liu X L，Lu H L，Wang W，et al.PTAS for the minimum kpath connected vertex cover problem in unit disk graphs[J].Journal of Global Optimization，2013，56（2）：449458

[9] Li X S，Zhang Z，Huang X H.Approximation algorithm for the minimum connected kpath vertex cover problem[C]∥International Conference on Combinatorial Optimization and Applications，2014：764771

[10] Chu Y，Fan J X，Liu W J，et al.PTAS for minimum kpath connected vertex cover in growthbounded graphs[C]∥International Conference on Algorithms and Architectures for Parallel Processing，2014：114126

[11] Wang L M，Zhang X Y，Zhang Z，et al.A PTAS for the minimum weight connected vertex cover P3problem on unit disk graphs[J].Theoretical Computer Science，2015，571：5866

[12] Zhang Z，Gao X F，Wu W L.PTAS for connected vertex cover in unit disk graphs[J].Theoretical Computer Science，2009，410（52）：53985402

[13] Jiang T，Wang L S.An approximation scheme for some steiner tree problems in the plane[J].Networks，1996，28（4）：187193

[14] Akyildiz I F，Pompili D，Melodia T.Underwater acoustic sensor networks：Research challenges[J].Ad Hoc Network，2005，3（3）：257279

[15] Wang L M，Du W X，Zhang Z，et al.A PTAS for minimum weighted connected vertex cover P3 problem in 3dimensional wireless sensor networks[J].Journal of Combinatorial Optimization，2017，33（1）：106122

[16] Zhang Z，Li X T，Shi Y S，et al.PTAS for minimum kpath vertex cover in ball graph[J].Information Processing Letters，2017，119：913

[17] Chang M S，Chen L H，Hung L J，et al.An O*（1.465 8n）time exact algorithm for the maximum boundeddegree1 set problem[C]∥Proceedings of the 31st Workshop on Combinatorial Mathematics and Computation Theory，2014：918

[18] Xiao M Y，Kou S W.Exact algorithms for the maximum dissociation set and minimum 3path vertex cover problems[J].Theoretical Computer Science，2017，657（A）：8697

[19] Bresar B，Kardos F，Katrenic J，et al.Minimum kpath vertex cover[J].Discrete Applied Mathematics，2011，159（12）：11891195

[20] Jakovac M.The kpath vertex cover of rooted product graphs[J].Discrete Applied Mathematics，2015，187（C）：111119

[21] Zuo L C，Zhang B T，Zhang S Q.The kpath vertex cover in product graphs of stars and complete graphs[J].International Journal of Applied Mathematics，2016，46：97103

[22] Brause C，KrivosBellus R.On a relation between kpath partition and kpath vertex cover[J].Discrete Applied Mathematics，2017，223：2838

[23] Bhavani P D，Kumar K V，Satyanarayana S.An investigation on some theorems on kPath vertex cover[J].Global Journal of Pure and Applied Mathematics，2016，12（2）：14031412

[24] Katrenic J.A faster FPT algorithm for 3path vertex cover[J].Information Processing Letters，2016，116（4）：273278

[25] Chang M S，Chen L H，Hung L J，et al.Fixedparameter algorithms for vertex cover P3[J].Discrete Optimization，2016，19：1222

[26] Tu J H，Jin Z M.An FPT algorithm for the vertex cover P4 problem[J].Discrete Applied Mathematics，2016，200（C）：186190

[27] Fellows M R，Guo J，Moser H，et al.A generalization of Nemhauser and Trotters local optimization theorem[J].Journal of Computer and System Sciences，2011，77（6）：11411158

[28] Chen J E，Fernau H，Shaw P，et al.Kernels for packing and covering problems[C]∥Frontiers in Algorithmics and Algorithmic Aspects in Information and Management，2012：199211

[29] Brause C，Schiermeyer I.Kernelization of the 3path vertex cover problem[J].Discrete Mathematics，2016，339：19351939

[30] Xiao M Y，Kou S W.Kernelization and parameterized algorithms for 3path vertex cover[C]∥International Conference on Theory and Applications of Models of Computation，2017：654668

[31] Tu J H，Yang F M.The vertex cover P3 problem in cubic graphs[J].Information Processing Letters，2013，113（13）：481485

[32] Li Y C，Tu J H.A 2approximation algorithm for the vertex cover P4 problem in cubic graphs[J].International Journal of Computer Mathematics，2014，91（10）：21032108

[33] Bresar B，KrivosBellus R，Semanisin G，et al.On the weighted kpath vertex cover problem[J].Discrete Applied Mathematics，2014，177：1418

[34] Li X S，Zhang Z，Huang X H.Approximation algorithms for minimum （weight） connected kpath vertex cover[J].Discrete Applied Mathematics，2016，205：101108

[35] Tu J H，Wu L D，Yuan J，et al.On the vertex cover P3 problem parameterized by treewidth[J].Journal of Combinatorial Optimization，2016，31（1）：112

[36] Bai Z W，Tu J H，Shi Y T.An improved algorithm for the vertex cover P3 problem on graphs of bounded treewidth[J].arXiv eprint，2016，arXiv：1603.09448

[37] Bhavan P D，Krishna G V，Thota N.Minimum kpath vertex using pruning algorithm[J].International Journal of Scientific Engineering and Technology Research，2014，3（46）：94199422

[38] Zhang Y P，Shi Y S，Zhang Z.Approximation algorithm for the minimum weight connected ksubgraph cover problem[J].Theoretical Computer Science，2014，535：5458